Урок геометрии в 11А классе
Дата: 16.10.18 Учитель: Эбушеитова Эльвира Меметовна
Тема: « Простейшие задачи в координатах»
Тип урока: закрепление темы «Простейшие задачи в координатах»
Вид урока: решение задач
Оборудование: мультимедиа, модели фигур.
Цели урока:
- способствовать совершенствованию навыков применения формул для вычисления длины вектора, нахождения координат середины отрезка;
- показать примеры решения стереометрических задач координатно-векторным методом.
Ход урока
I. Организационный момент
Сообщить тему урока, сформулировать цели урока.
II. Проверка домашнего задания
№432*
III.Актуализация опорных знаний
1. Теоретический опрос:
а) Вывести формулу координат середины отрезка.
б) Вывести формулу длины отрезка.
в) Какие названия у осей в пространстве?
г) Как определить коллинеарность векторов через их координаты?
1) аˉ{3;-2;5}и вˉ{-6;4;-10}; 2) Найти m и n сˉ{1;m;3}и
dˉ {5;-10;n}если векторы коллинеарны.
d) Укажите координаты точки А(x,y,z)если она
1) на оси абсцисс, оси ординат, оси аппликат.
2) в плоскости ОХУ,ОУZ,ОХZ
IV .Решение задач
№429(слайд11) №431,(слайд9,10) Задача № 431 б),№440(проверить правильность самостоятельного решения показав на экране)
№1.Дано: ΔАВС; А(3; 7; -А), В(5; -3; 2), С(1; 3; -10).
Определить вид ΔABC.
Решение: 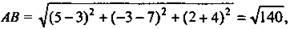
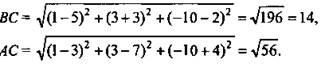
Проверим равенство BС3 = AC2 + AB2; 196 = 140 + 56 верно ⇒ по теореме обратной теоремы Пифагора сделаем вывод, что ΔABC прямоугольный с прямым углом А.
№2.Дано:  MNK ; M (2; –1; 0), N (3; –2; 1), К (0; 1;4).
MNK ; M (2; –1; 0), N (3; –2; 1), К (0; 1;4).
Определить вид  MNK.
MNK.
Решение: Сравним длины сторон: MN =  =
= 
NK= =
= 
MK= =
= 
NK MK MN –  MNK – разносторонний.
MNK – разносторонний.
Проверим верно ли равенство: NK2 = MK2 + MN2 = 27 = 24 + 3 = 27 = 27 =  MNK – прямоугольный.
MNK – прямоугольный.
V.Физкультминутка (проводит ученик)
Укажи всевозможные способы решения задач.
№3. Доказать, что четырехугольник с вершинами А(6;7;8), В(8;2;6), С(4;3;2),Д(2;8;4)является ромбом.(еще как можно сформулировать задачу?)
Докажите, что четырехугольник ABCD является ромбом, если A(6; 7; 8), B(8; 2; 6), C(4; 3; 2), D(2; 8; 4).
Решение:
 смежные стороны равны
смежные стороны равны
Найдем середину отрезка BD и AC:
2. Середина отрезков BD и AC точка O(5;5;5). Диагонали точкой пересечения делятся пополам в параллелограмме. Четырехугольник ABCD – ромб. Проверим, не квадрат ли это?
Решение: BD = 
BD2 = AB2 + AD2 76 = 33 + 33 =
ABCD – не квадрат
№4*(решит векторно-координатным способом) Дана прямоугольная призма АВСА1В1С1 высота которой 6 см, катеты в основании по 2см.М-середина В1С1, К-середина АС. Найти длину МК.
VI. Постановка домашнего задания.
П.49 повторить,№430,431(в),436*(схему работу наметить усилиями детей)
VII.Тестирование.
VIII.Подведение итогов, рефлексия.





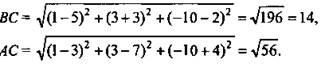
 смежные стороны равны
смежные стороны равны









