Простые числа-удивительные числа

Простые числа -удивительные числа

Презентацию подготовила

ученица 10 «А» класса

МОУ «СОШ № 76»

Ганина Мария

Руководитель: Ковалевская О.Н.

Цель работы

Изучение истории простых чисел и исследование некоторых свойств простых чисел.

Для достижения данной цели я поставила следующие задачи:

• Исследовать множество простых чисел.
• Изучить исторические сведения о простых числах.
• Выяснить, существует ли самое большое простое число.
• Изучить сопутствующую теорию и историческое развитие данной темы.
• Изучить метод «Решето Эратосфена».
• Исследовать современное состояние изучаемого вопроса.

Теоретические сведения

• Простое число — это натуральное число, которое имеет ровно 2 натуральных делителя ( только 1 и самого себя ). Составное число — натуральное число большее 1, не являющееся простым.
• Простое число — это натуральное число, которое имеет ровно 2 натуральных делителя ( только 1 и самого себя ).
• Составное число — натуральное число большее 1, не являющееся простым.

• – особое число , оно не является ни простым, ни составным
• – особое число , оно не является ни простым, ни составным

Таким образом, все натуральные числа, за исключением единицы, разбиваются на простые и составные. Изучением свойств простых чисел занимается теория чисел.

Простые числа-близнецы это пара простых чисел, отличающихся на 2.

Если натуральное число a делится на натуральное число b,то число b называют делителем числа a, а число а – кратным числа b.

Вместо содержания я буду говорить эту цитату

«Среди чисел существует такое совершенство и согласие, что нам надо размышлять дни и ночи

над их удивительной закономерностью». Стевин

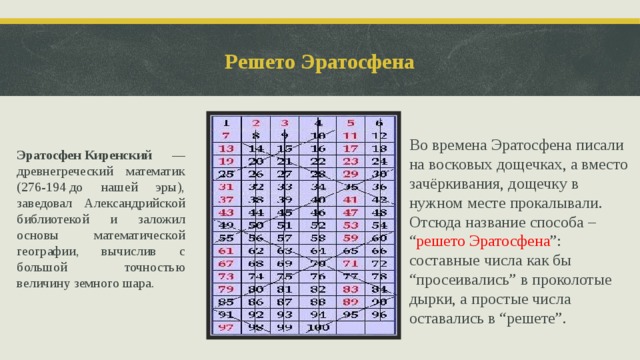
Решето Эратосфена

Во времена Эратосфена писали на восковых дощечках, а вместо зачёркивания, дощечку в нужном месте прокалывали. Отсюда название способа – “ решето Эратосфена ”: составные числа как бы “просеивались” в проколотые дырки, а простые числа оставались в “решете”.

Эратосфен Киренский —древнегреческий математик (276-194 до нашей эры), заведовал Александрийской библиотекой и заложил основы математической географии, вычислив с большой точностью величину земного шара.

Свойство простых чисел

1. Числа - «близнецы» ( два числа, отличаются на 2,

н-р 5 и 7, 11 и 13, 17 и 19 и т.д.).

2. Числа- «тройняшки» (три числа, отличаются на 2, н-р 3, 5, 7).

3. Палиндромические числа – каждое равно обращённому. Например: 11,101, 131, 151, 181 и т.д.

4. Симметричные себе простые числа: 107 – 701, 113 – 311, 149 – 941, 157 – 751 и др.

5. Любое четное число, больше 2, можно представить в виде суммы 2-х простых чисел.

Например: 4=2+2, 6=3+3, 8=5+3, 10=3+7, 12=5+7 и т.д.

6. Любое нечетное число больше 5, можно представить в виде суммы трех простых чисел.

Например: 7=2+3+2, 9=2+5+2, 11=5+3+3 и т.д.

Теорема Евклида

Евклид - древнегреческий математик, автор первого из дошедших до нас теоретических трактатов по математике. Биография, сведения о нем крайне скудны. Его научная деятельность протекала в Александрии в 3 веке до н. э.

Евклид — первый математик александрийской школы.

Теорема.

Евклид доказал, что простых чисел бесконечно много . Можно сказать также, что среди простых чисел нет самого большого числа .

Так две с лишним тысячи лет назад Евклид лишил математиков надежды получить когда-нибудь полный список простых чисел.

Много ученых пытались найти общую формулу для записи простых чисел, но все их попытки не увенчались успехом.

Самое большое простое число

Самое большое известное простое число содержит 17 425 170 цифр. Автором открытия этого простого числа стал Кертис Купер из Университета Центрального Миссури в Уорренсбурге. Новым рекордсменом стало так называемое простое число Мерсенна равное  – 1.

Леонард Эйлер (15 апреля 1707 - 7(18) сентября 1783)

Швейцарский, немецкий и российский математик и механик, внёсший фундаментальный вклад в развитие многих наук. Благодаря Эйлеру в математику вошли общая теория рядов, фундаментальная « формула Эйлера » в теории  комплексных чисел , операция сравнения по целому модулю , полная теория  непрерывных дробей и д.р. Он создал несколько новых математических дисциплин —  теорию чисел ,  вариационное исчисление и многое другое

Решето Эйлера

[2] (3) 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59 61 63 65 67 69 71 73 75 77 79 ...

[3] (5) 7 11 13 17 19 23 25 29 31 35 37 41 43 47 49 53 55 59 61 65 67 71 73 77 79 ...

[4] (7) 11 13 17 19 23 29 31 37 41 43 47 49 53 59 61 67 71 73 77 79 ...

[5] (11) 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 ... [...]

Решето Эйлера это вариант решета Эратосфена, в котором каждое составное число удаляется из списка только один раз.

После  k -го этапа рабочий список содержит только числа взаимно простые с первыми k  простыми числами (то есть числа не кратные ни одному из первых  k  простых чисел), и начинается с  (k+1) -го простого числа. Все числа в списке, меньшие квадрата его первого числа, являются простыми.

ДИРИХЛЕ Петер Густав Лежён (1805—1859)

немецкий математик, иностранный член-корреспондент Петербургской АН (1837)

В 1837 г. доказал, что в любой арифметической прогрессии, первый член и разность которой взаимно просты, есть бесконечно много простых чисел.

Заключение

В результате, проделанной работы, я пришла к следующим выводам:

Простые числа не совсем соответствуют значениям и определению слова «простой». По своей сути они очень сложны, многогранны и хранят много тайн, неизвестного. Простые числа –это как бы кирпичики, из которых строятся все остальные числа.

Для простых чисел не существует формулы, по которой их можно вычислить и последовательность простых чисел бесконечна. Многие ученые на протяжении многих веков вносили свой вклад в изучение простых чисел. В настоящее время исследование темы продолжается.

Спасибо за внимание!