| Вариант 1 1. Дан параллелепипед ABCDA1B1C1D1. Укажите вектор с началом и концом в вершинах параллелепипеда, равный: 1) 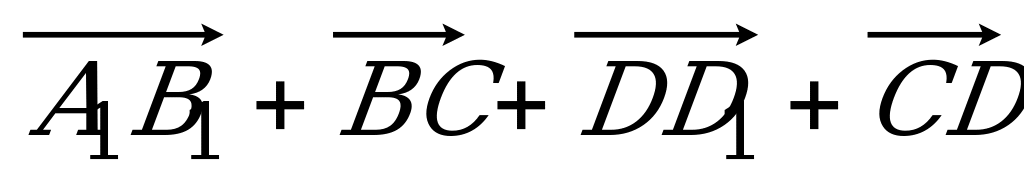 ; 2) ; 2) 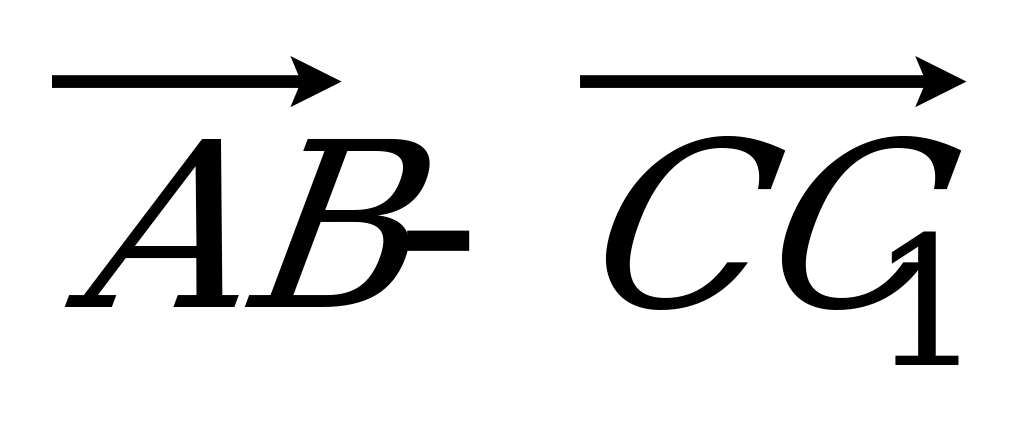 . . 2. DABC – тетраэдр. Точка М – середина ребра ВС, точка N – середина отрезка DМ. Выразите вектор 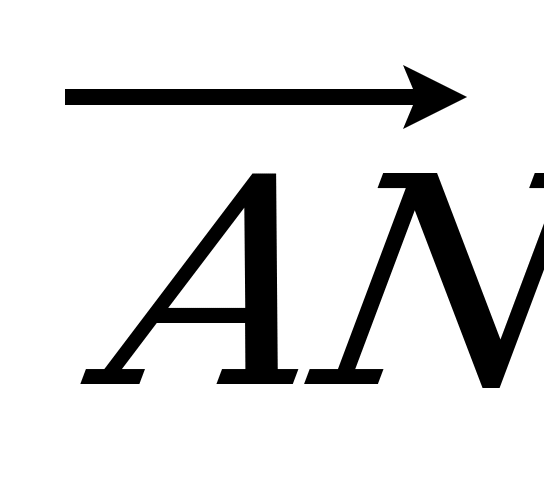 через векторы через векторы 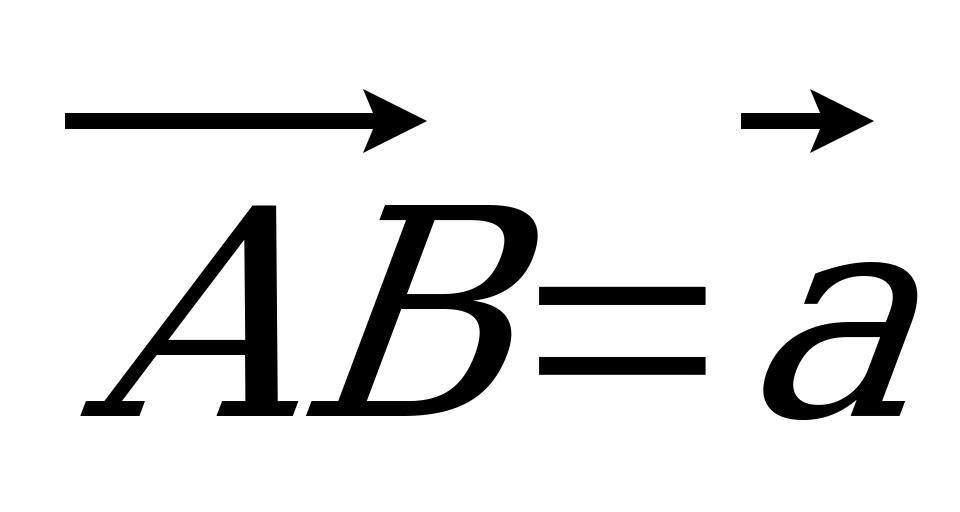 , , 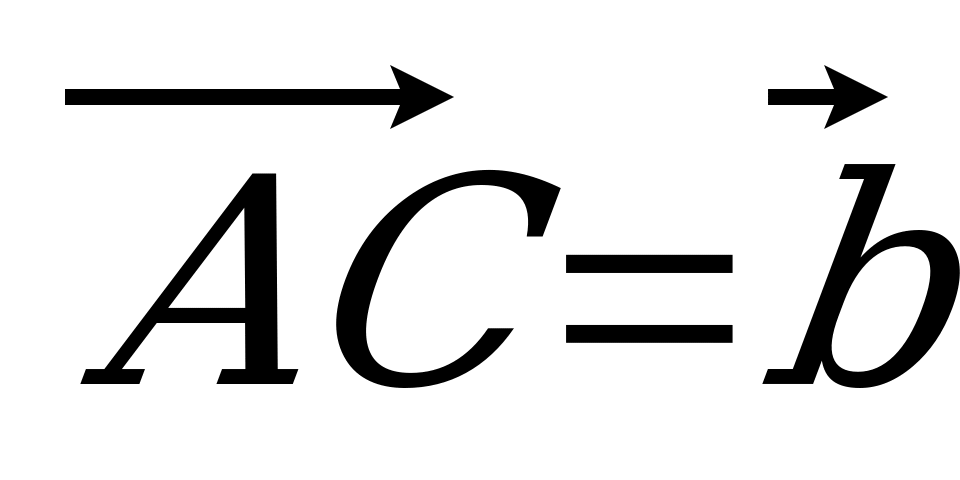 , , 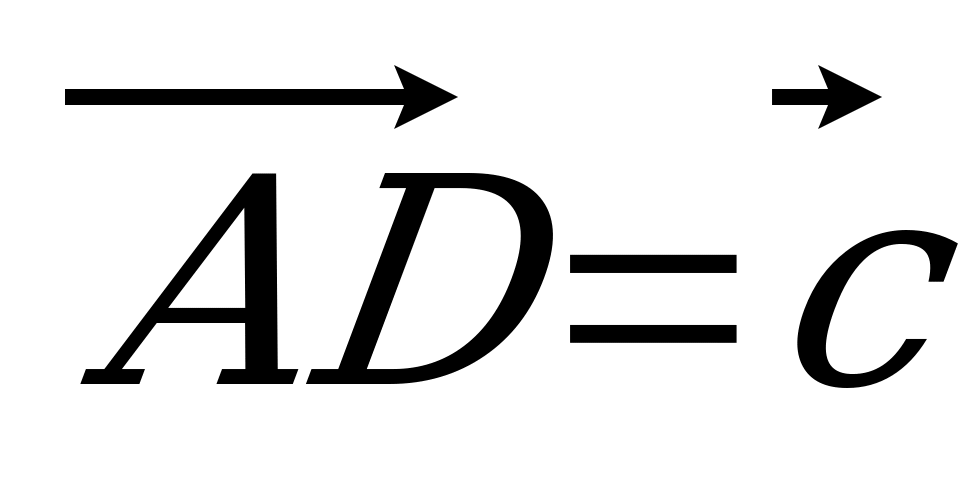 . . 3. Медианы BDC пересекаются в точке Р, точка K – середина отрезка AP (точка А не лежит в плоскости BDC). Разложите вектор 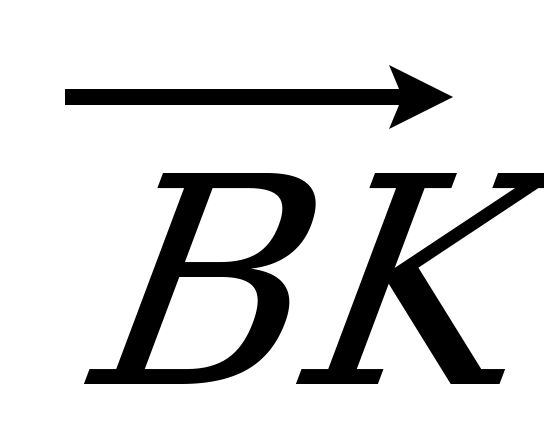 по векторам по векторам 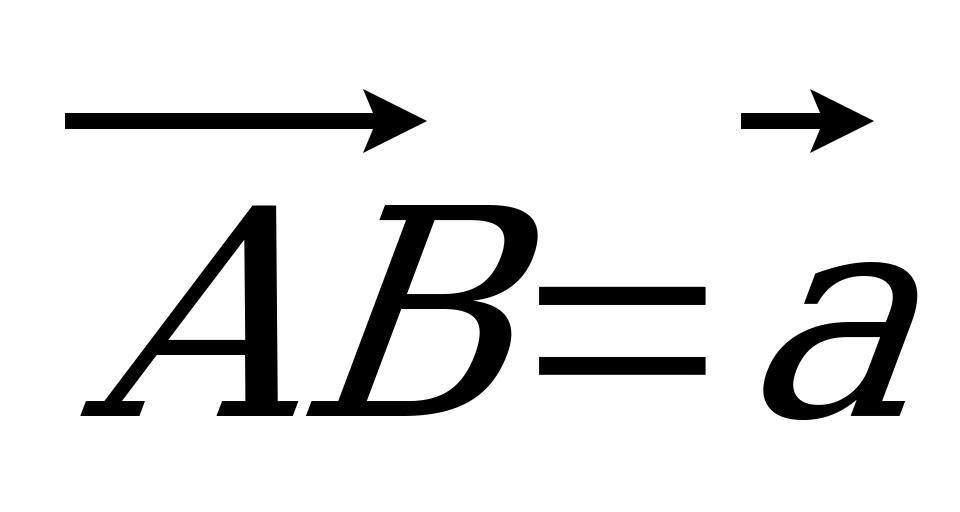 , , 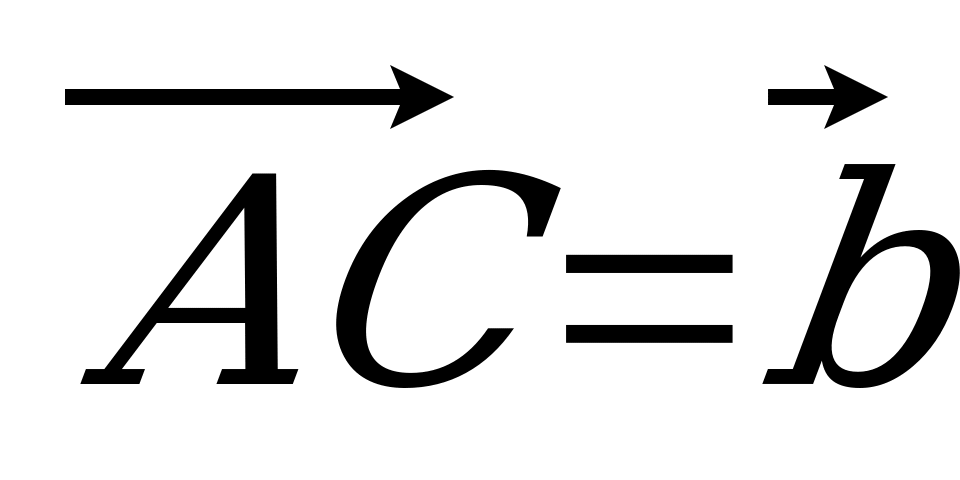 , , 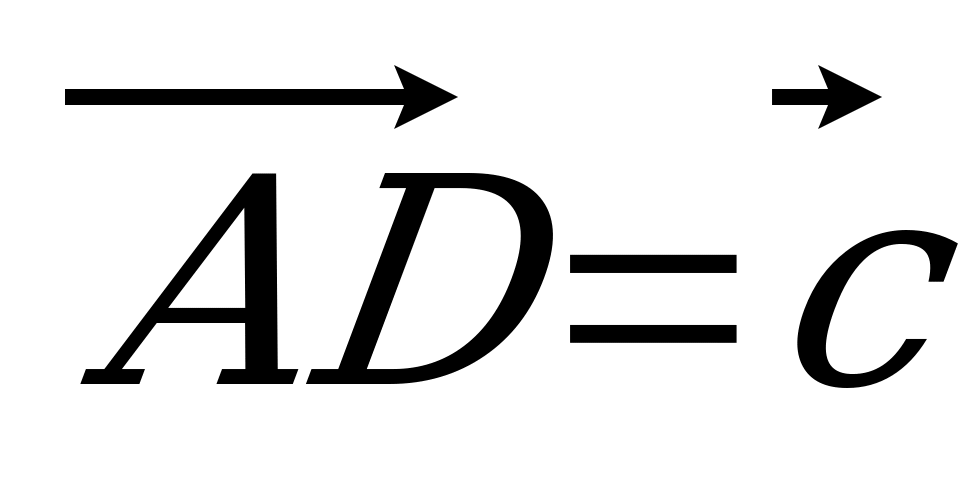 . . 4. В параллелепипеде ABCDA1B1C1D1 М лежит на BB1, причем BМ : МB1 = 3 : 4, а Р лежит на B1D1, причем B1P : РD1 = 2 : 1. Разложите вектор  по векторам по векторам 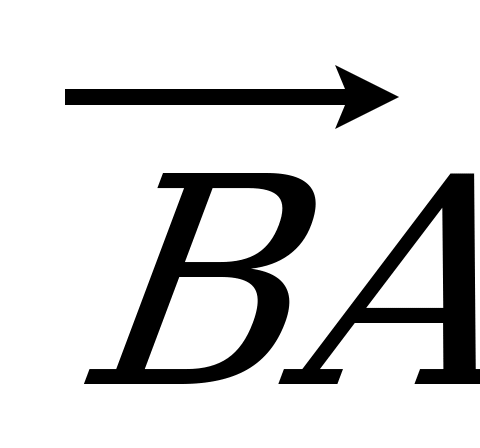 , , 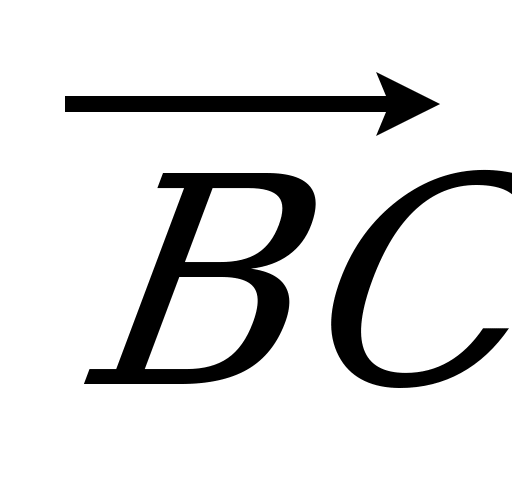 и и  . . | Вариант 2 1. ABCDA1B1C1D1 – параллелепипед. Изобразите на рисунке векторы, равные: 1) 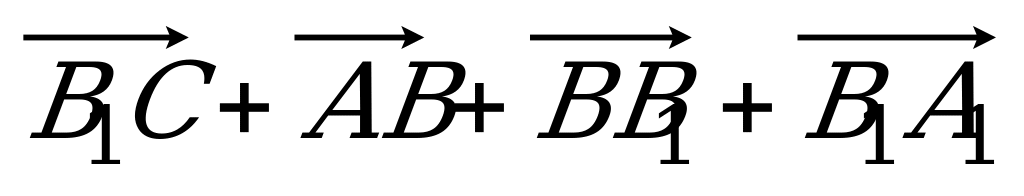 ; 2) ; 2) 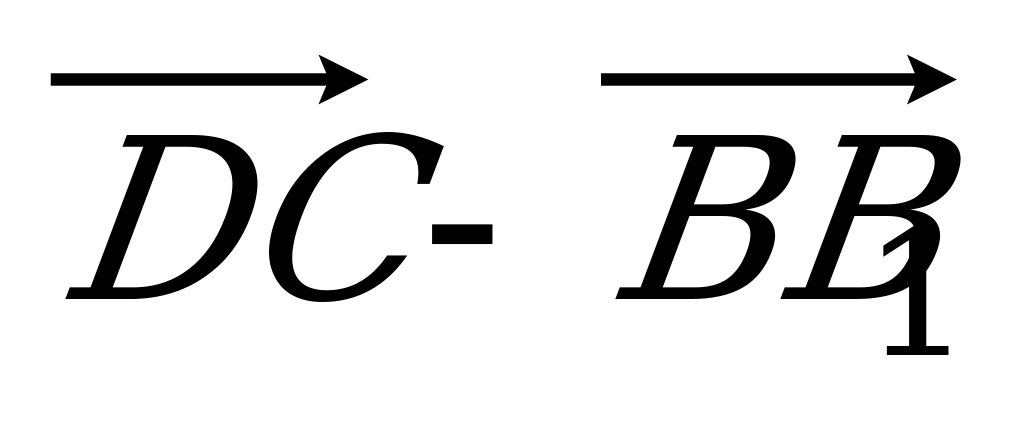 . . 2. В тетраэдре DABC точка N – середина ребра AB, точка P – середина отрезка DN. Выразите вектор  через векторы через векторы 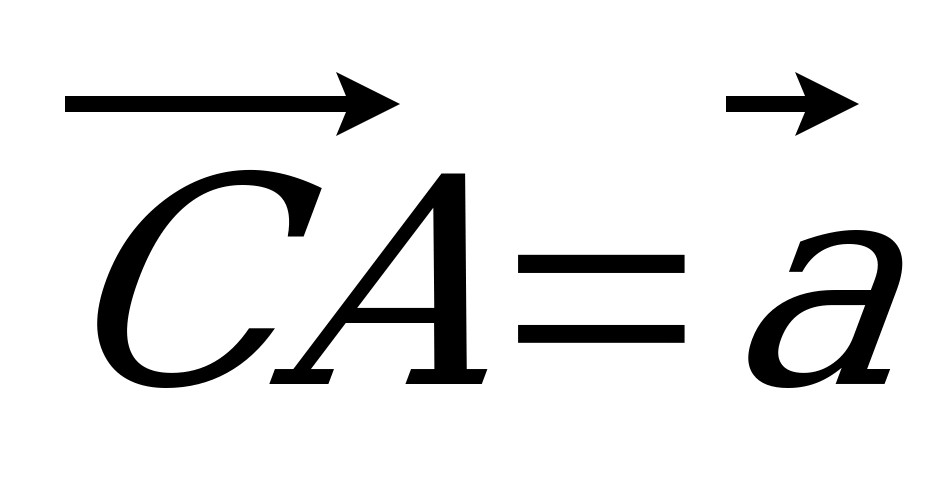 , , 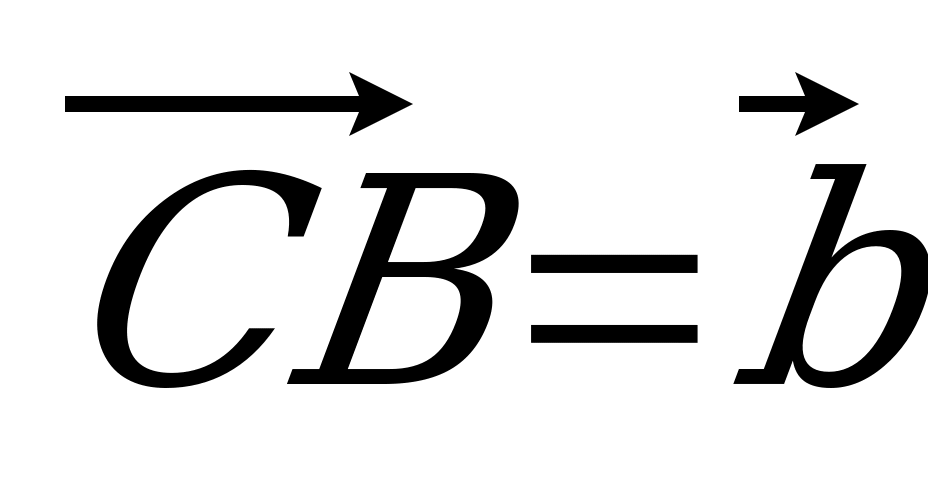 , , 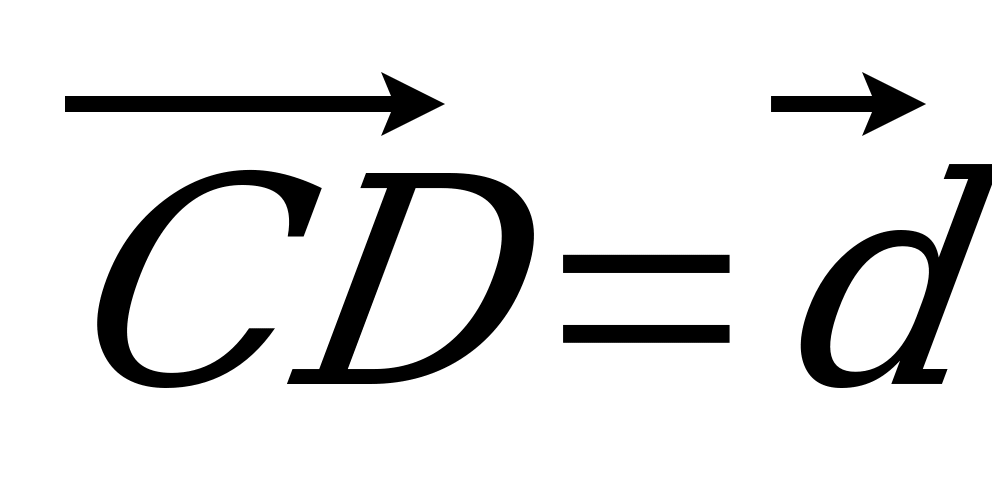 . . 3. Медианы грани DBC тетраэдра DABC пересекаются в точке О, точка R – середина отрезка AO. Разложите вектор 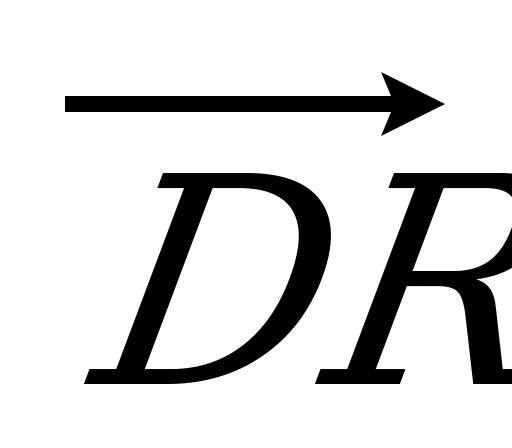 по векторам по векторам 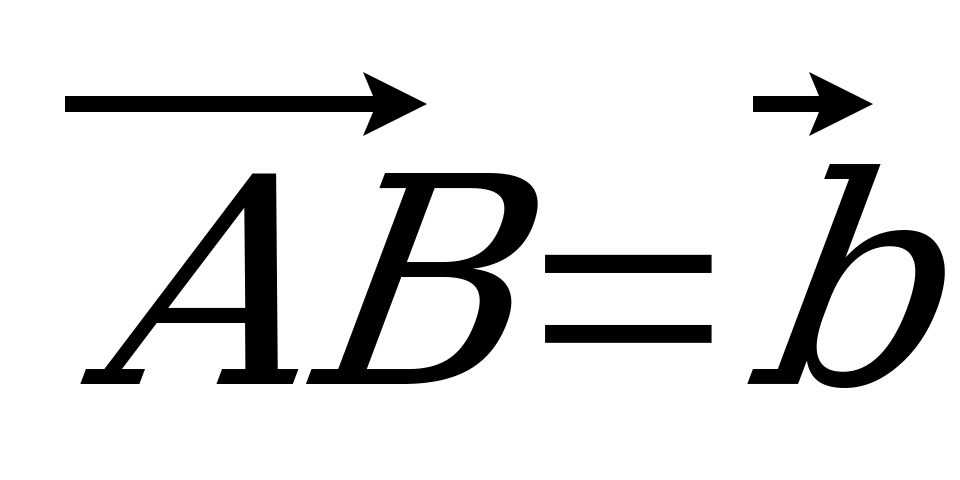 , , 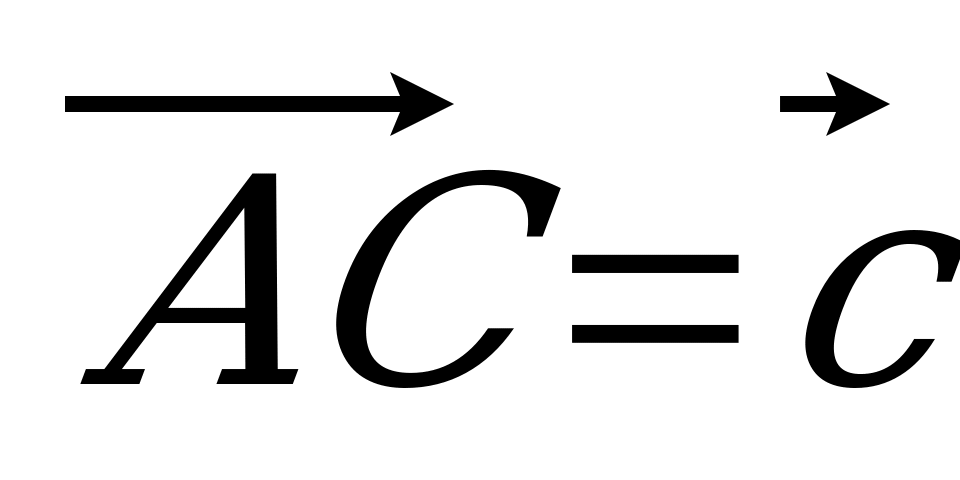 , , 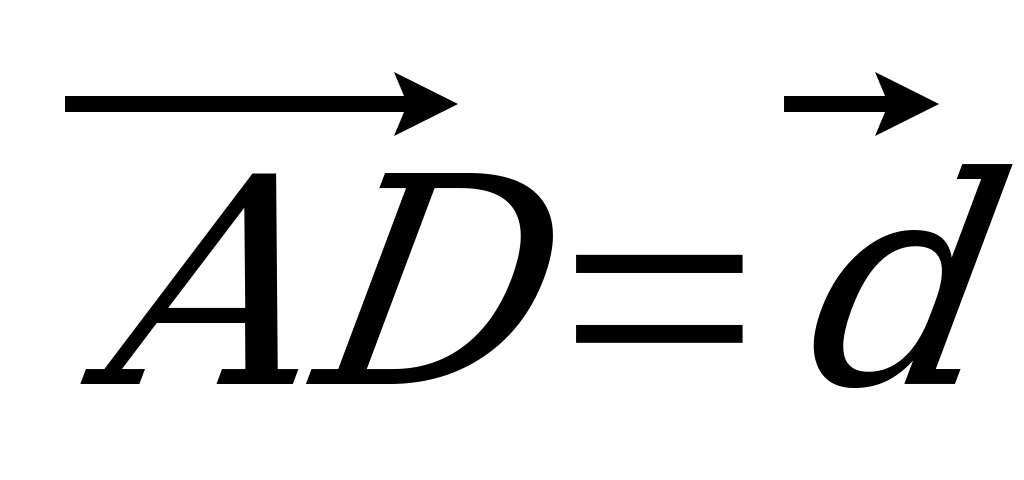 . . 4. Дан параллелепипед ABCDA1B1C1D1. Точка М лежит на AB, причем AМ : МB = 5 : 2, а K AD1, причем AK : КD1 = 3 : 5. Разложите вектор 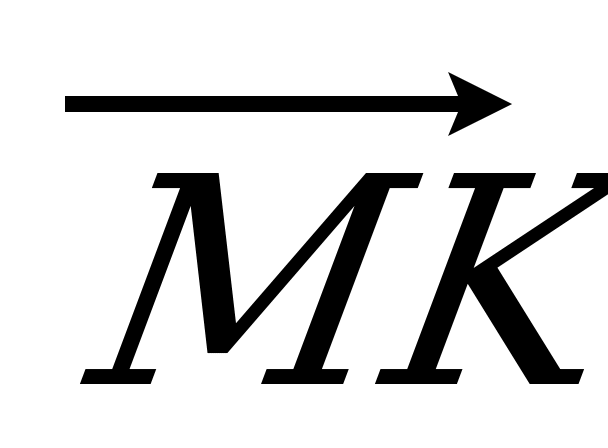 по векторам по векторам 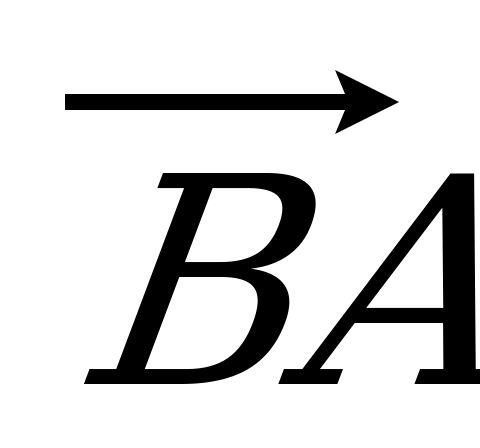 , ,  и и 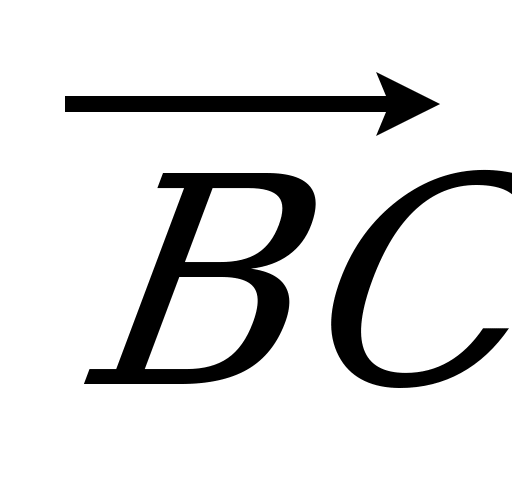 . . |
| Вариант 3 1. ABCDA1B1C1D1 – параллелепипед. Изобразите на рисунке векторы, равные: 1) 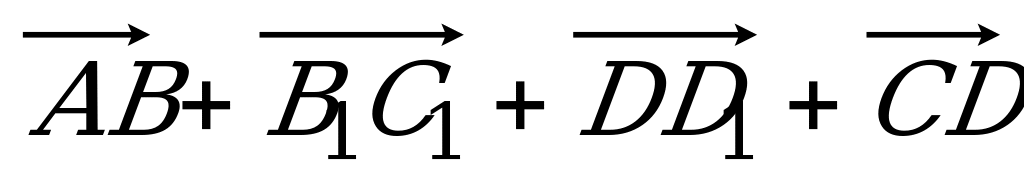 ; 2) ; 2) 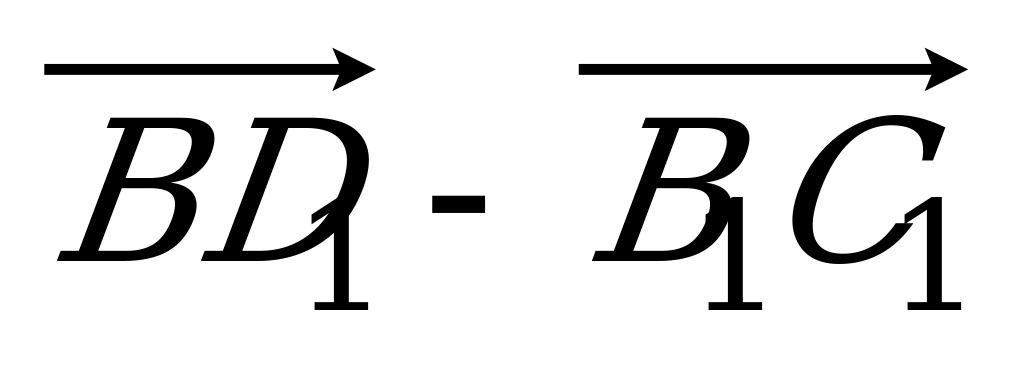 . . 2. Точка S – середина ребра AС тетраэдра DABC, точка N – середина отрезка DS. Выразите вектор 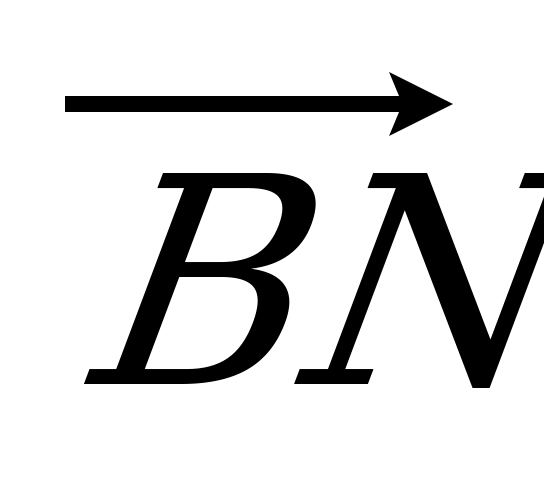 через векторы через векторы 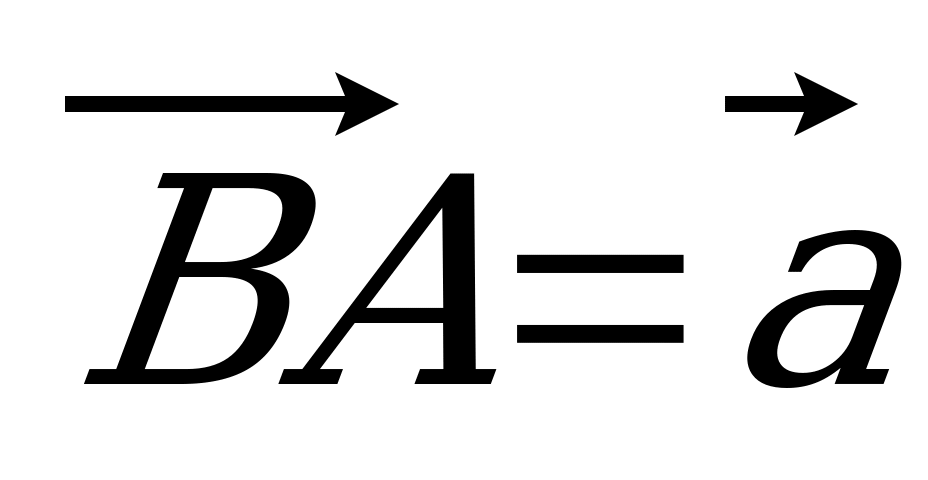 , , 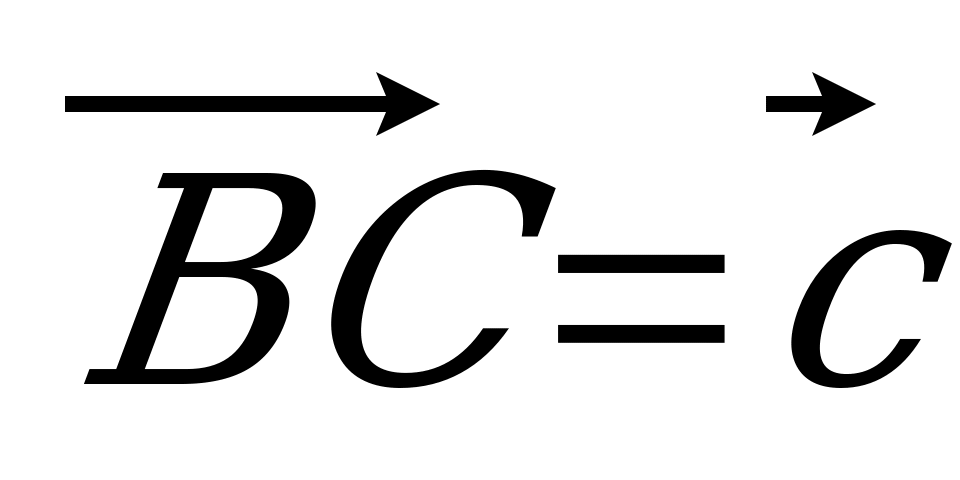 , , 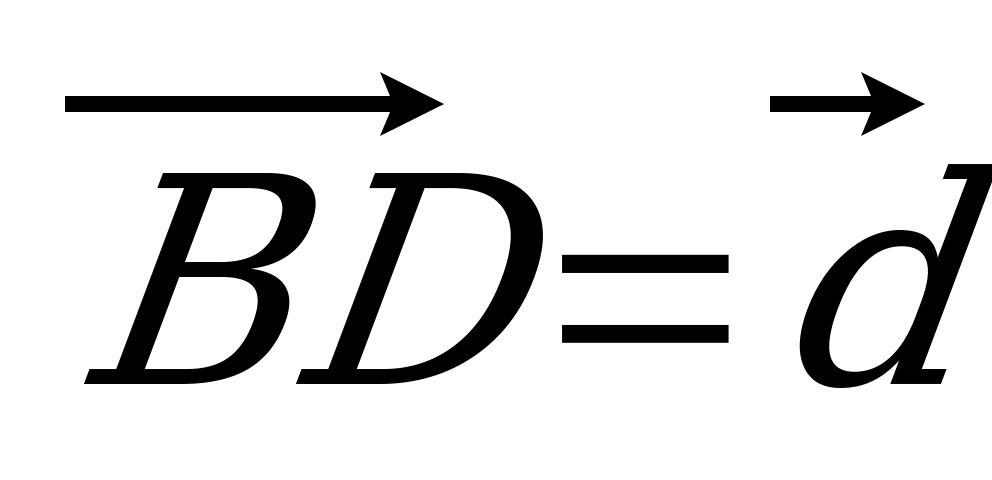 . . 3. В треугольнике KLM точка С – пересечение медиан, T – середина отрезка NС (N не лежит в плоскости KLM). Разложите 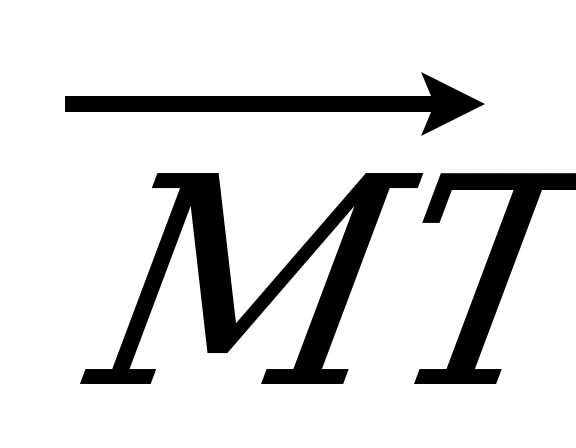 по векторам по векторам 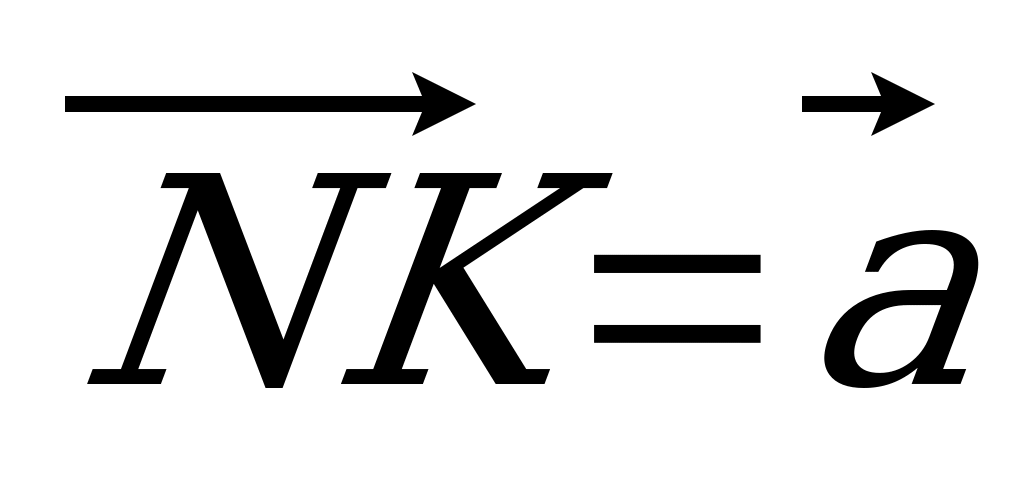 , , 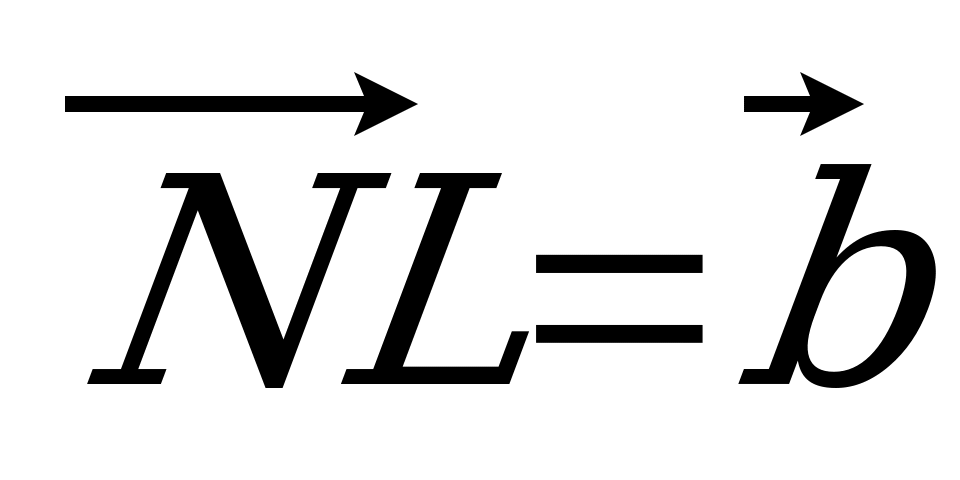 , , 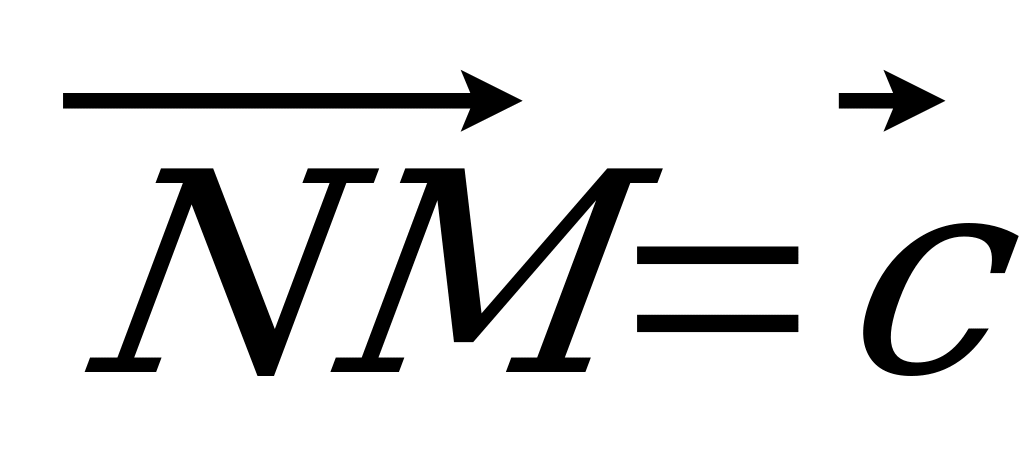 . . 4. В параллелепипеде ABCDA1B1C1D1 точка N делит CC1 так, что CN : NC1 = 1 : 3, а точка H делит A1С1 так, что А1Н : НС1 =
= 5 : 2. Разложите вектор  по векторам по векторам 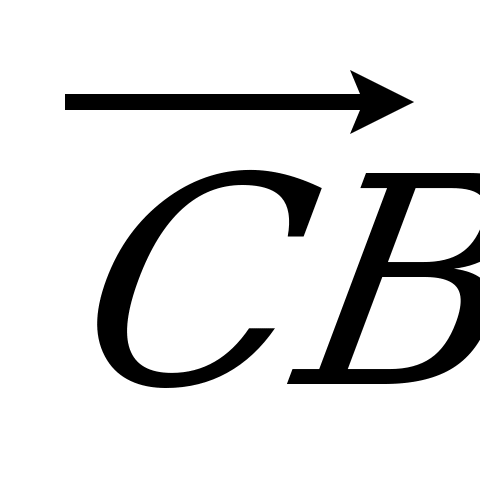 , , 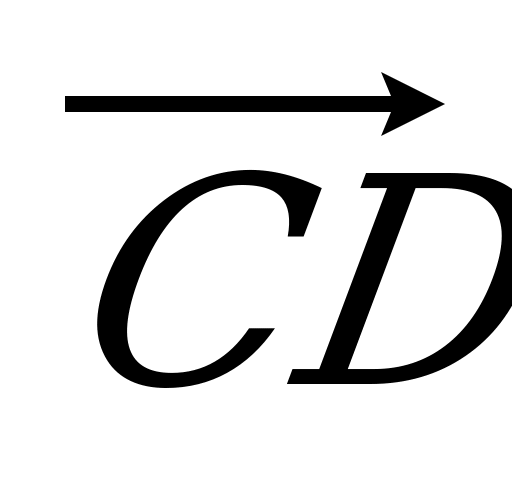 и и  . . | Вариант 4 1. Укажите вектор с началом и концом в вершинах параллелепипеда ABCDA1B1C1D1, равный: 1) 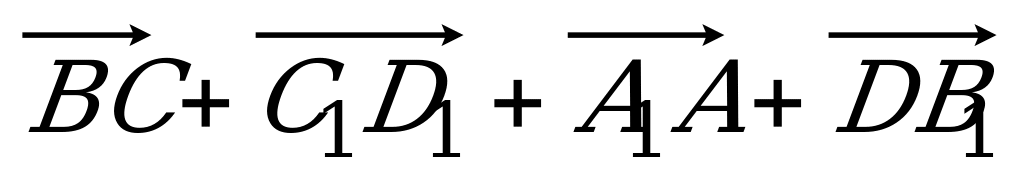 ; 2) ; 2) 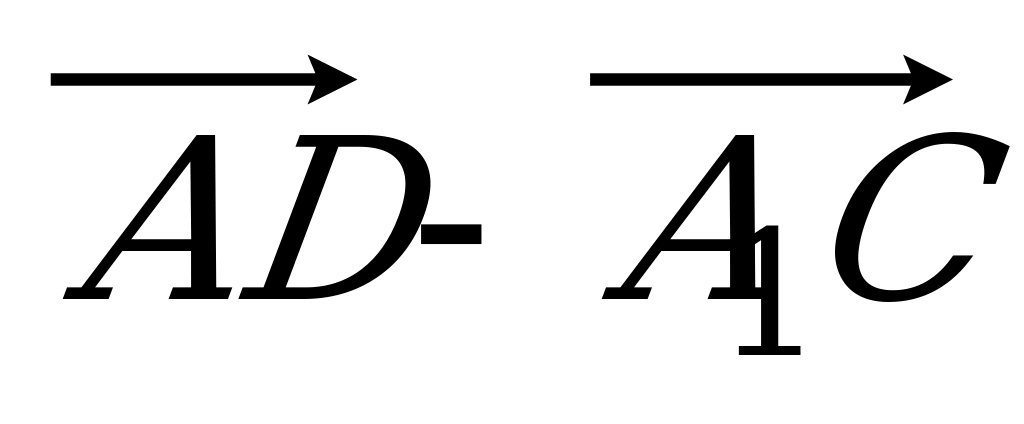 . . 2. Дан тетраэдр DABC. Точка P – середина ребра AB, точка R – середина отрезка CP. Выразите вектор 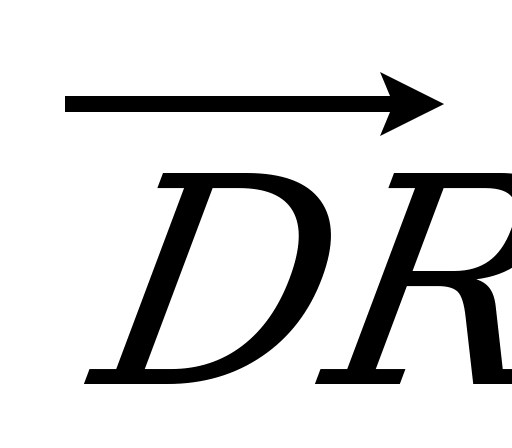 через векторы через векторы 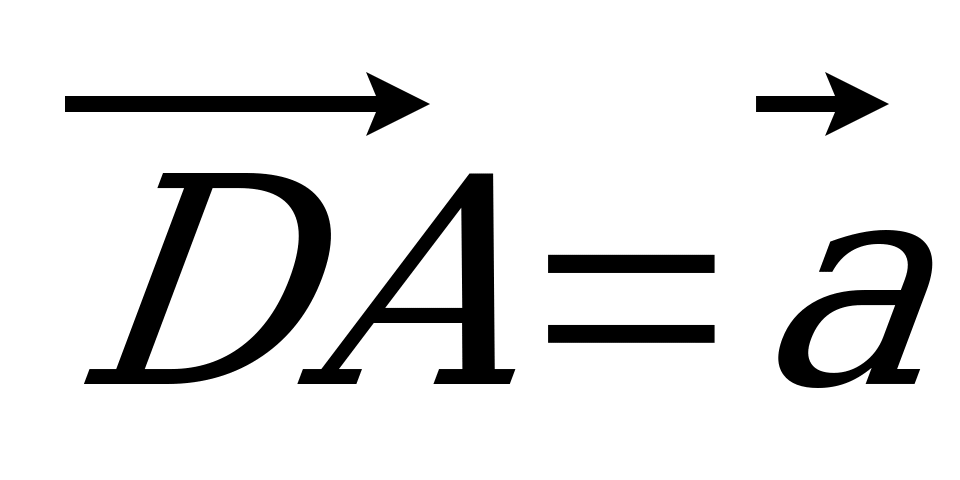 , , 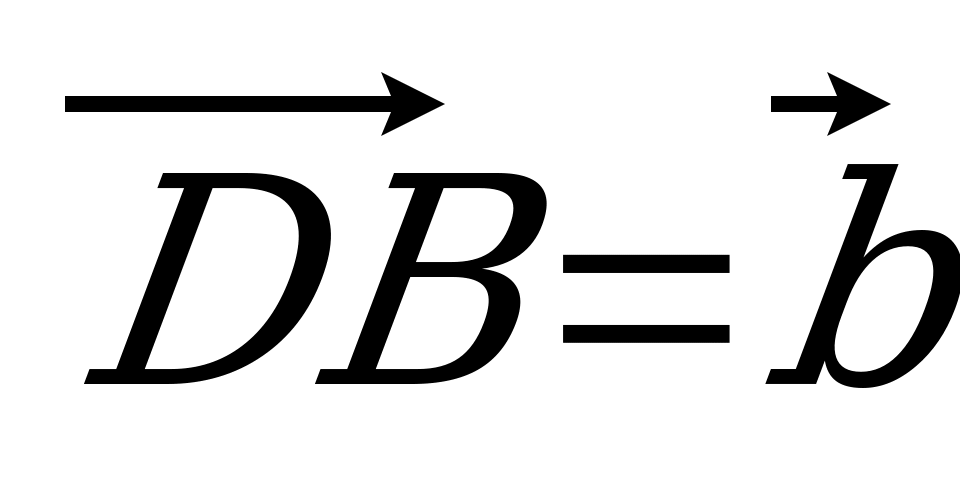 , , 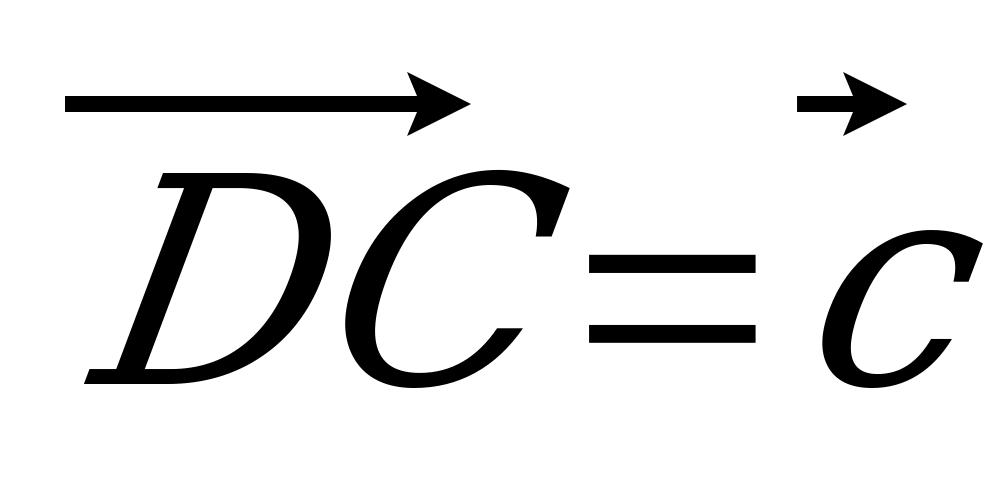 . . 3. DABC – тетраэдр. Медианы грани DAB пересекаются в точке N, точка O – середина отрезка CN. Разложите вектор 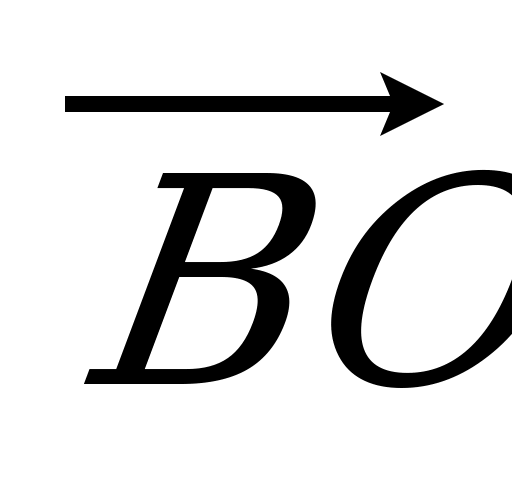 по векторам по векторам 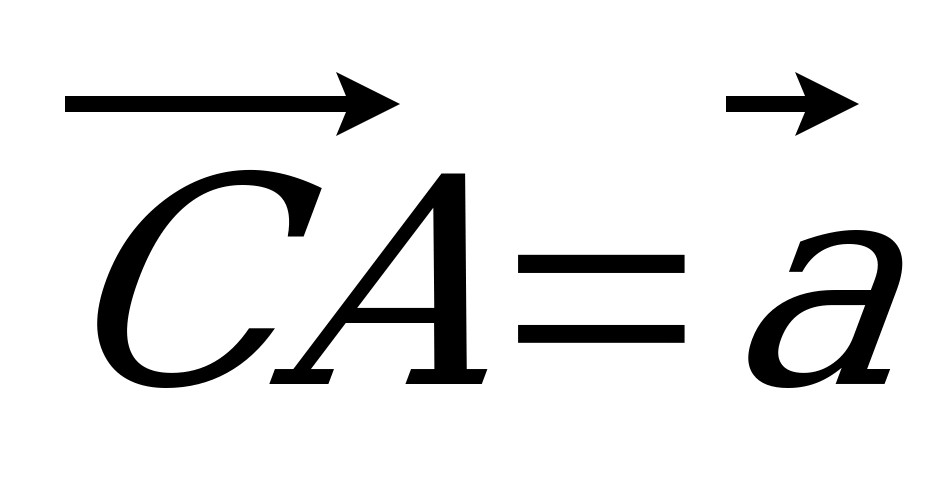 , , 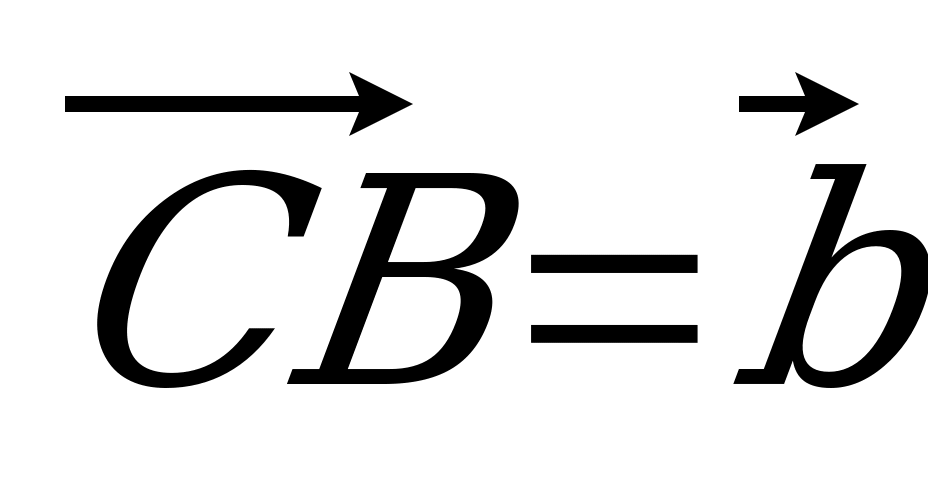 , , 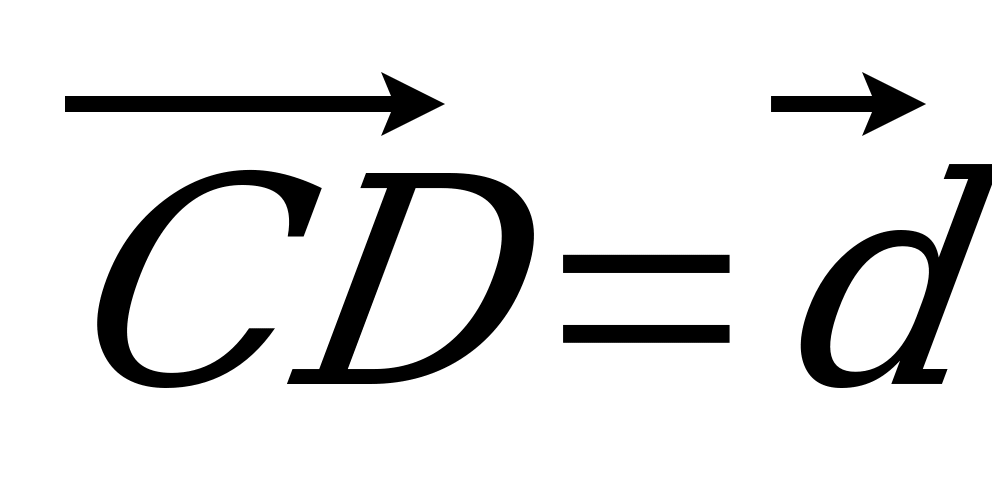 . . 4. ABCDA1B1C1D1 – параллелепипед. Точка E лежит на ребре DC так, что DE : EC = 1 : 4, а F СB1, причем CF : FB1 =
= 2 : 3. Разложите вектор  по векторам по векторам 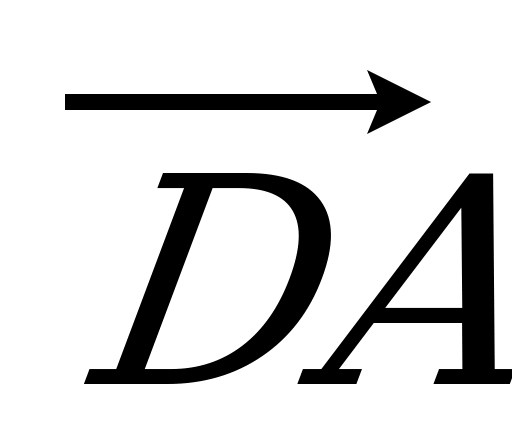 , , 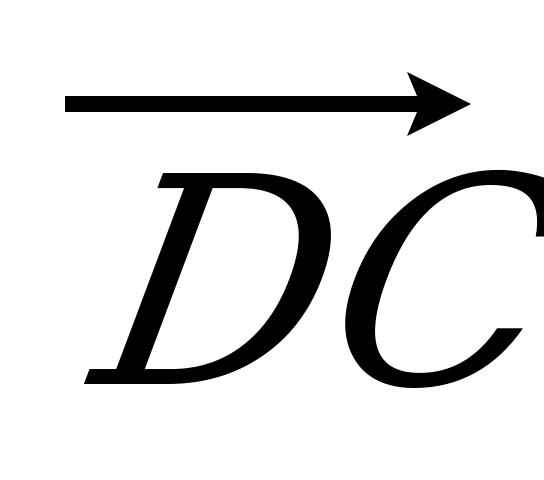 и и  . . |
| Вариант 5 1. ABCDA1B1C1D1 – параллелепипед. Изобразите на рисунке векторы, равные: 1) 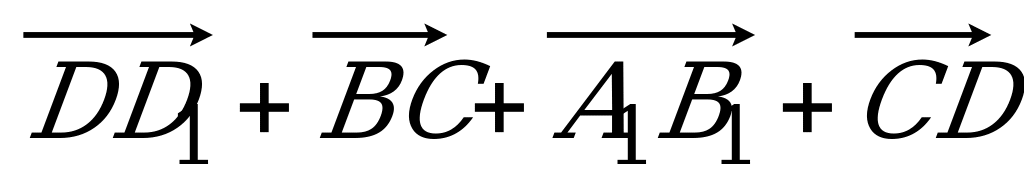 ; 2) ; 2) 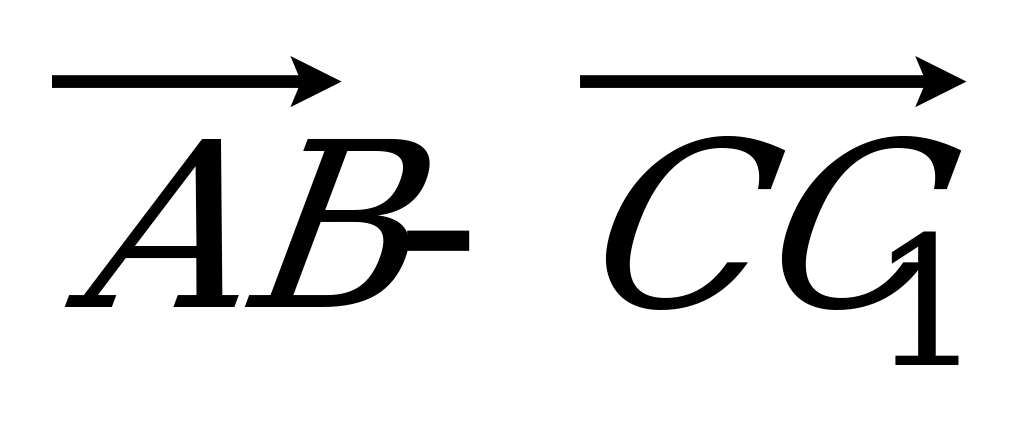 . . 2. На середине ребра ВС тетраэдра DABC лежит точка T, а на середине отрезка DT – точка H. Выразите вектор 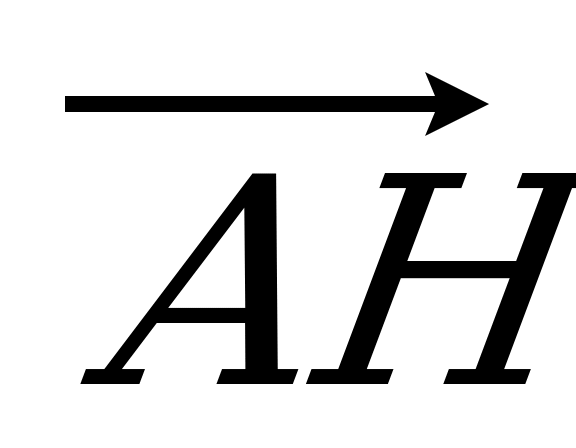 через векторы через векторы 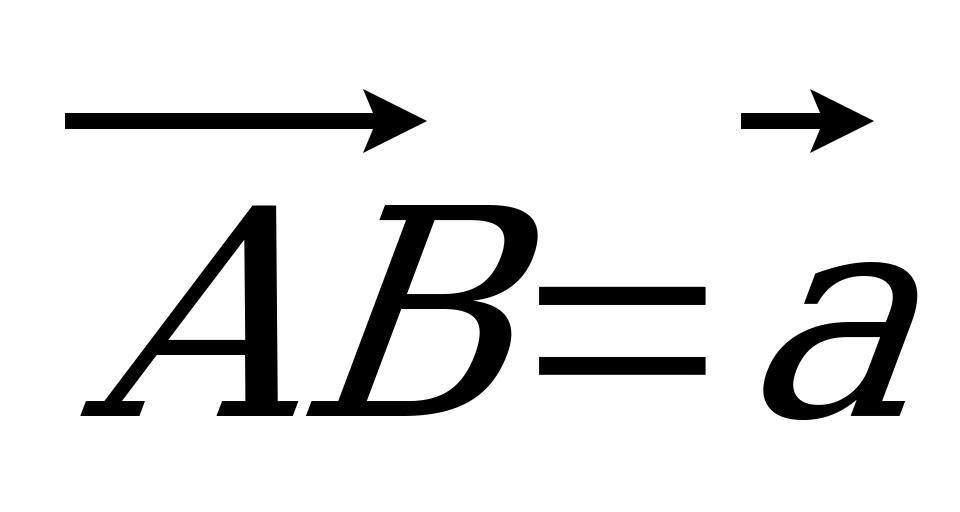 , , 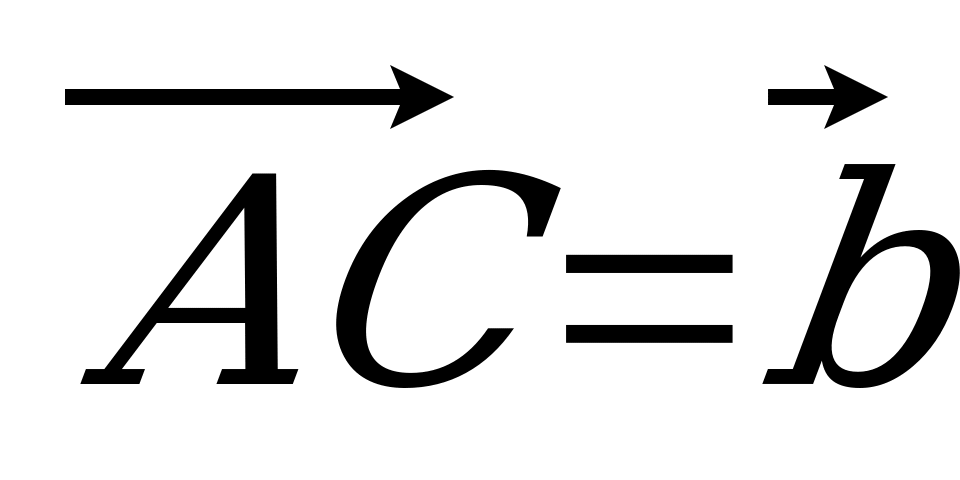 , , 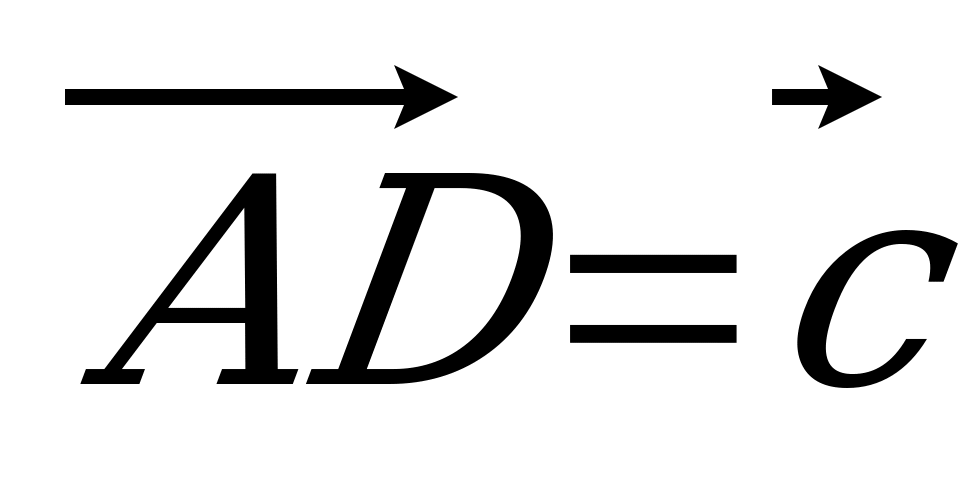 . . 3. R – точка пересечения медиан треугольника SPQ, M – середина отрезка FR (точка F не лежит в плоскости SPQ). Разложите вектор 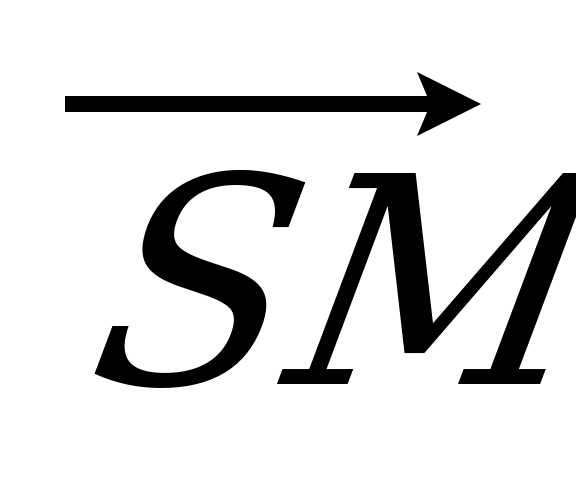 по векторам по векторам 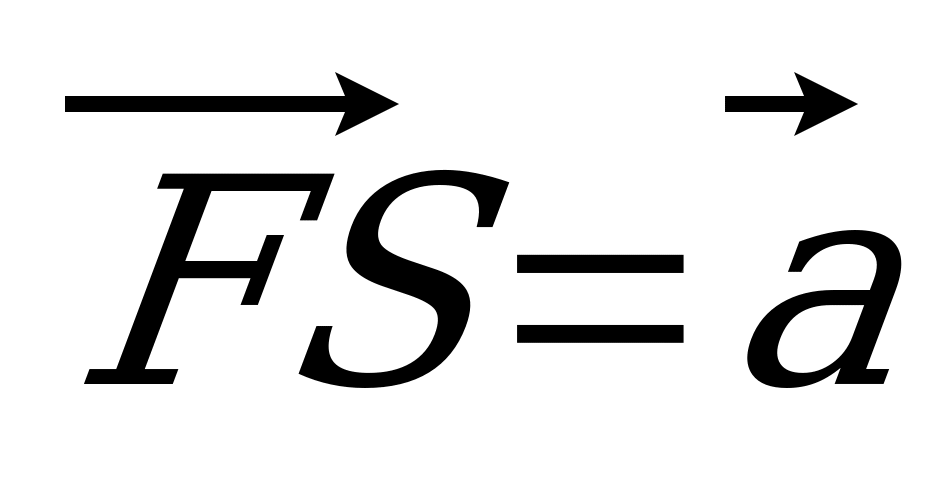 , , 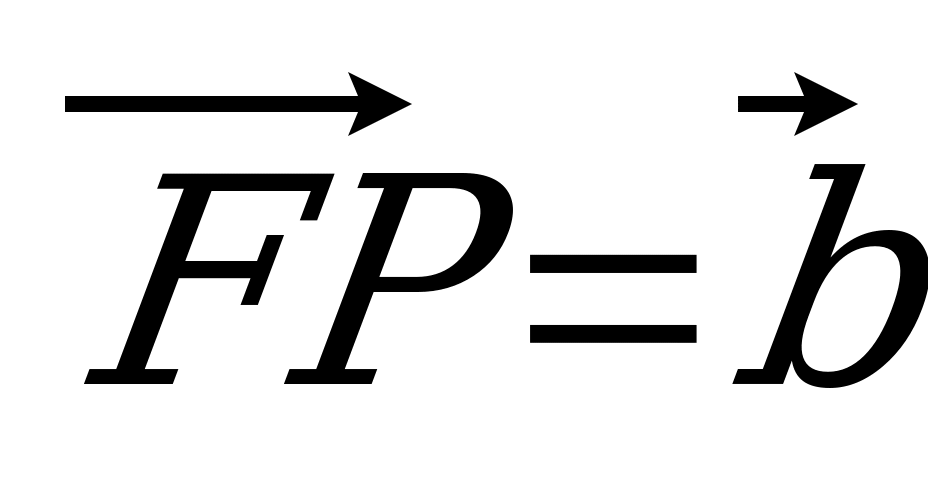 , , 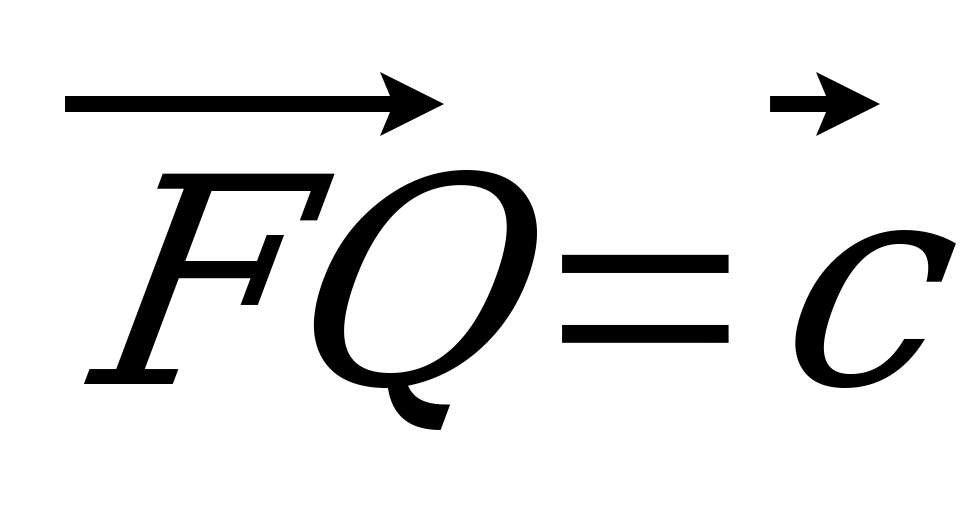 . . 4. Точка K лежит на ребре BB1 параллелепипеда ABCDA1B1C1D1 так, что BK : KB1 = 3 : 4, а N D1B1, причем D1N : NB1 = 1 : 2. Разложите вектор  по векторам по векторам 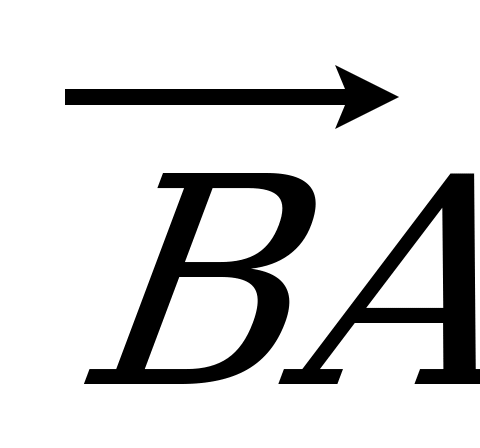 , , 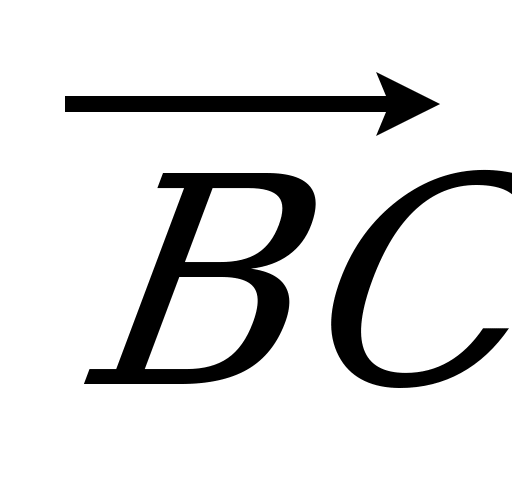 и и  . . | Вариант 6 1. Дан параллелепипед ABCDA1B1C1D1. Укажите вектор с началом и концом в вершинах параллелепипеда, равный: 1) 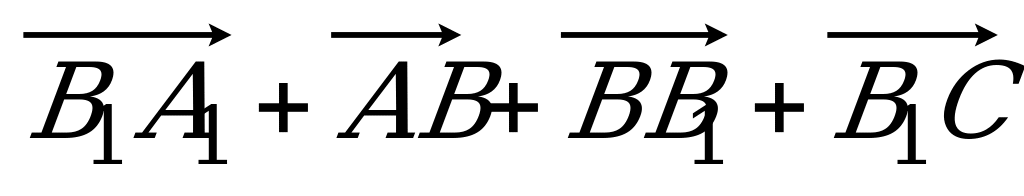 ; 2) ; 2) 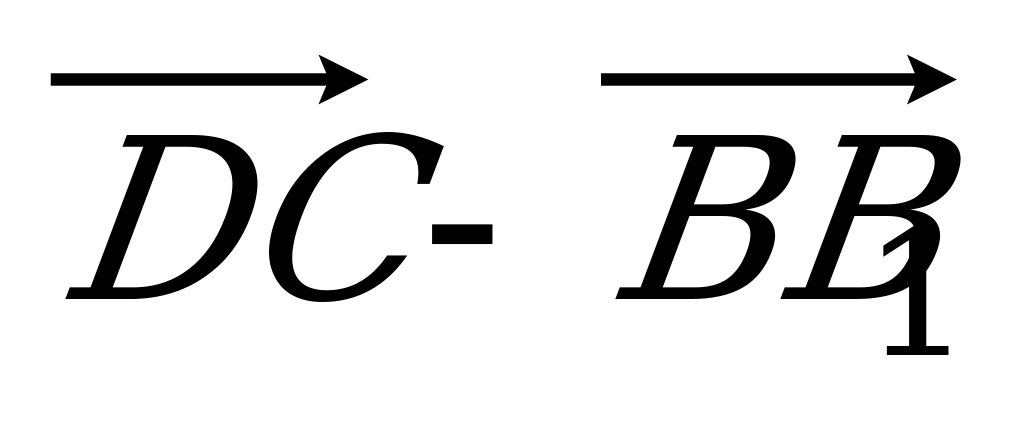 . . 2. DABC – тетраэдр. На середине ребра AB лежит точка К, точка M – середина отрезка DK. Выразите вектор  через векторы через векторы 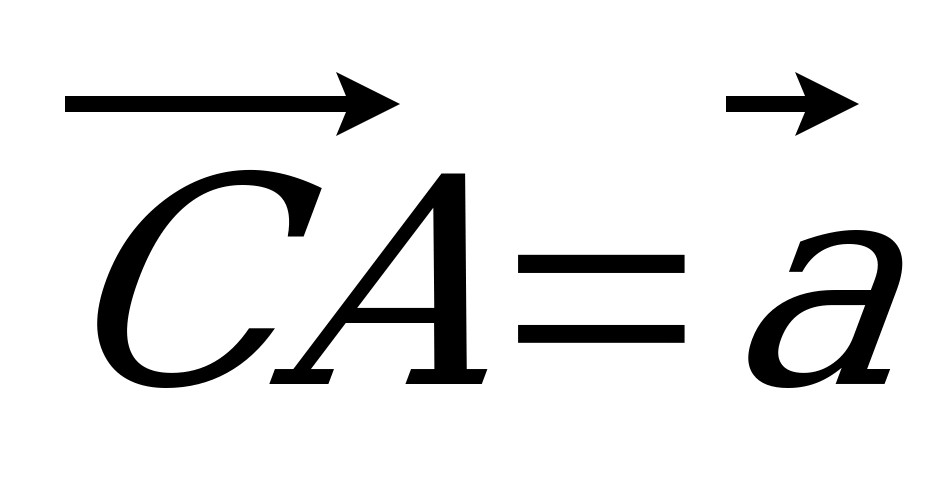 , , 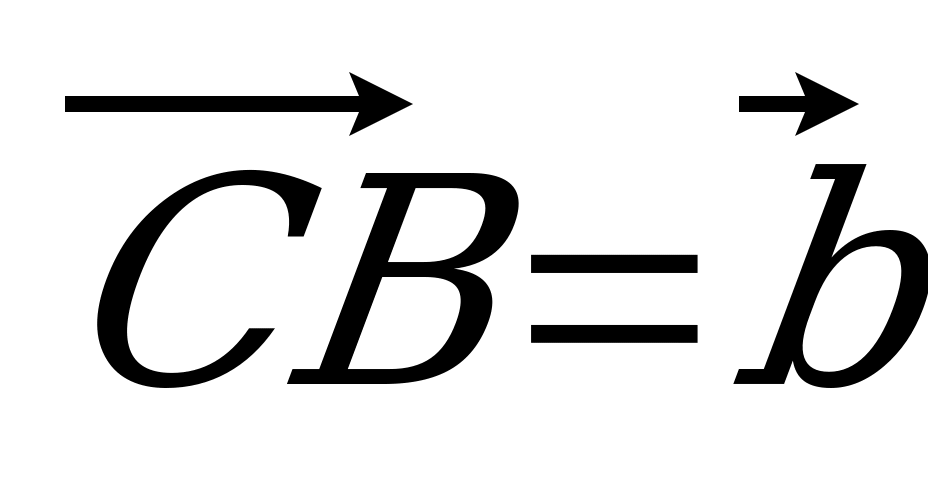 , , 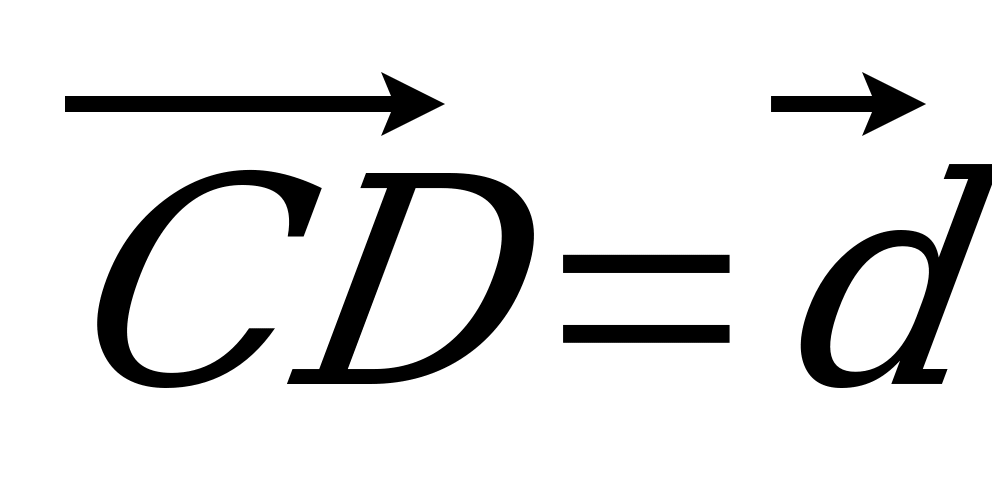 . . 3. В тетраэдре ABCD медианы грани DBC пересекаются в точке E, на середине отрезка AE лежит точка N. Разложите вектор  по векторам по векторам 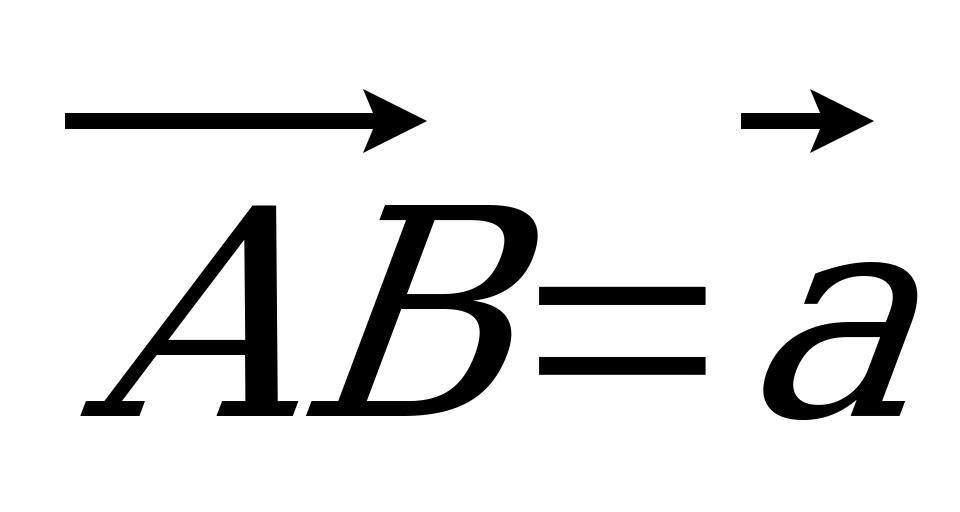 , , 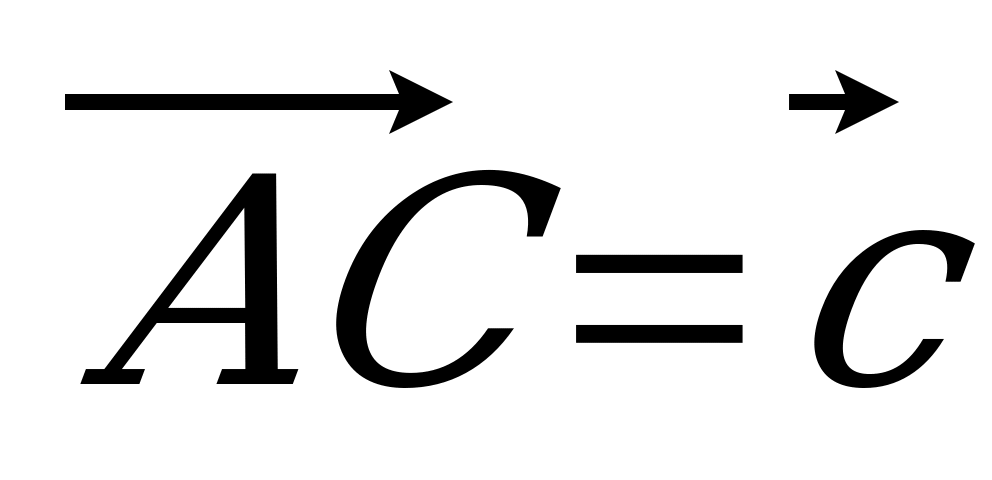 , , 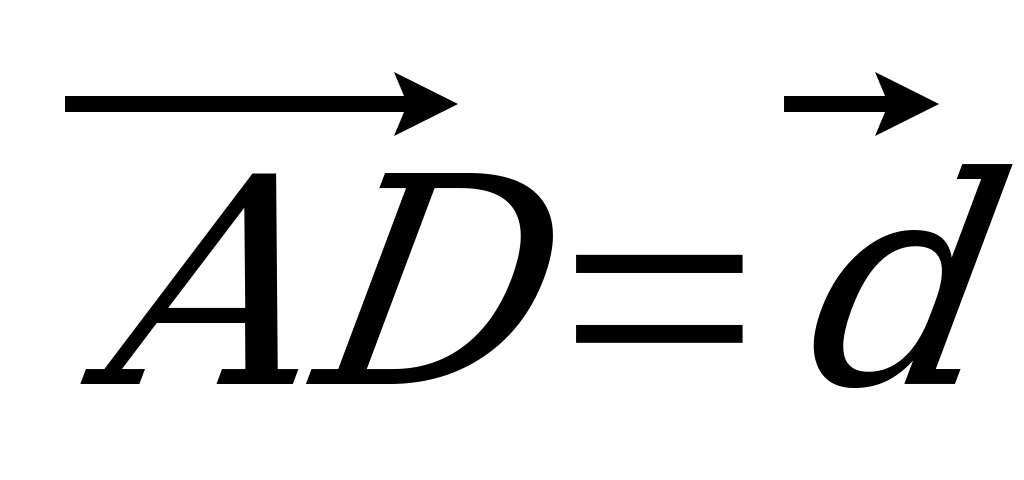 . . 4. Точка S лежит на ребре BA, а точка Р лежит на диагонали AD1 параллелепипеда ABCDA1B1C1D1, BS : SA = 2 : 5, AP : РD1 =
= 3 : 5. Разложите вектор 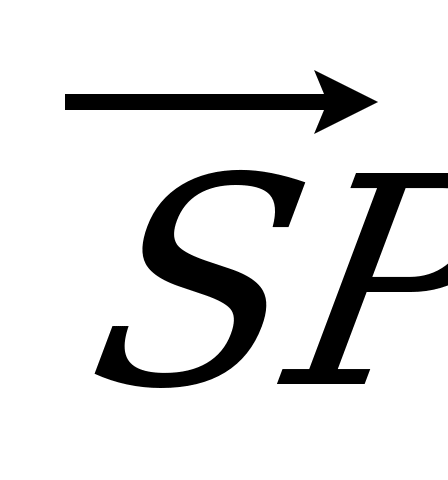 по векторам по векторам 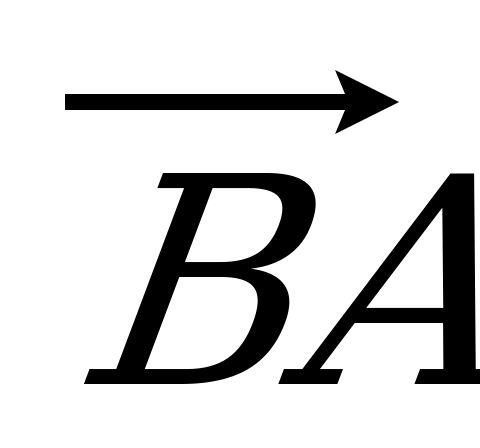 , , 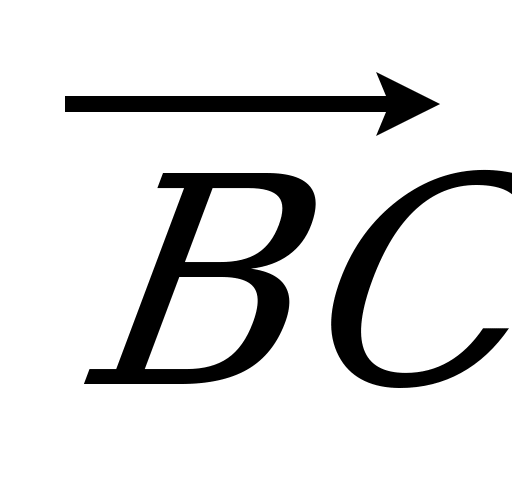 и и 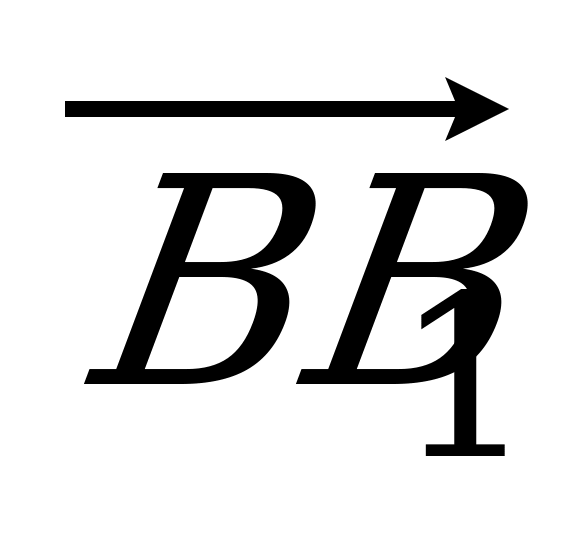 . . |
| Вариант 7 1. Изобразите параллелепипед ABCDA1B1C1D1. Постройте на рисунке векторы, равные: 1) 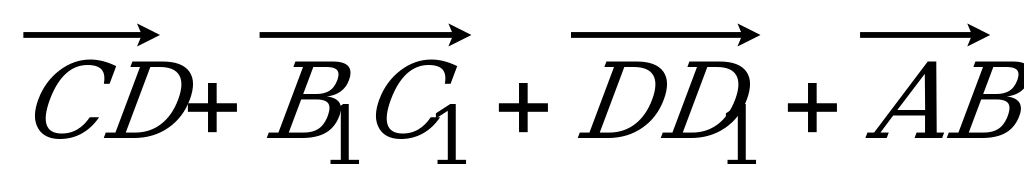 ; 2) ; 2) 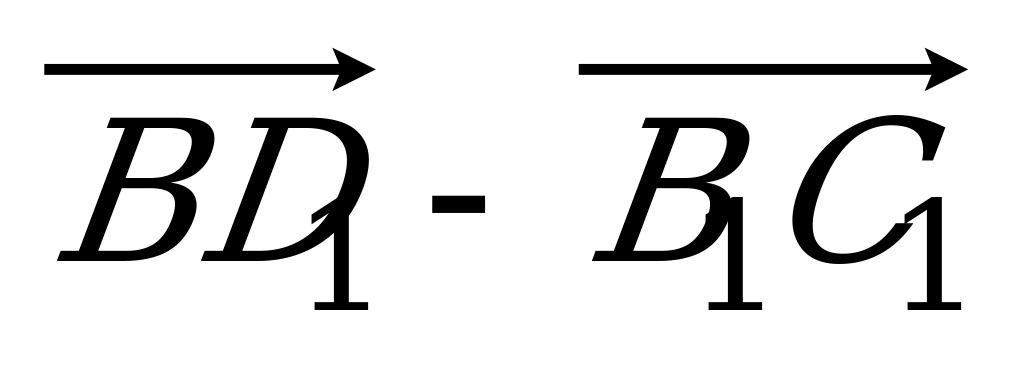 . . 2. В тетраэдре DABC на середине ребра AС лежит точка T, а на середине отрезка DT – точка K. Разложите вектор 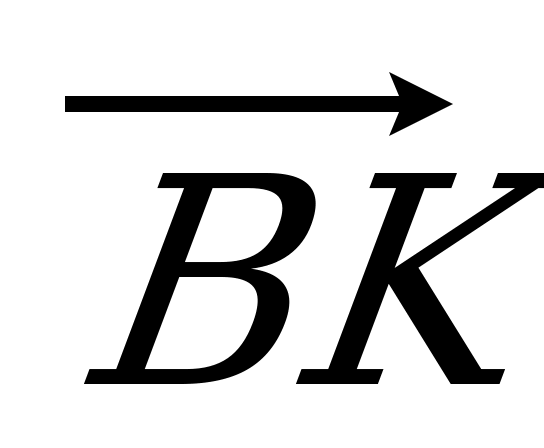 по векторам по векторам 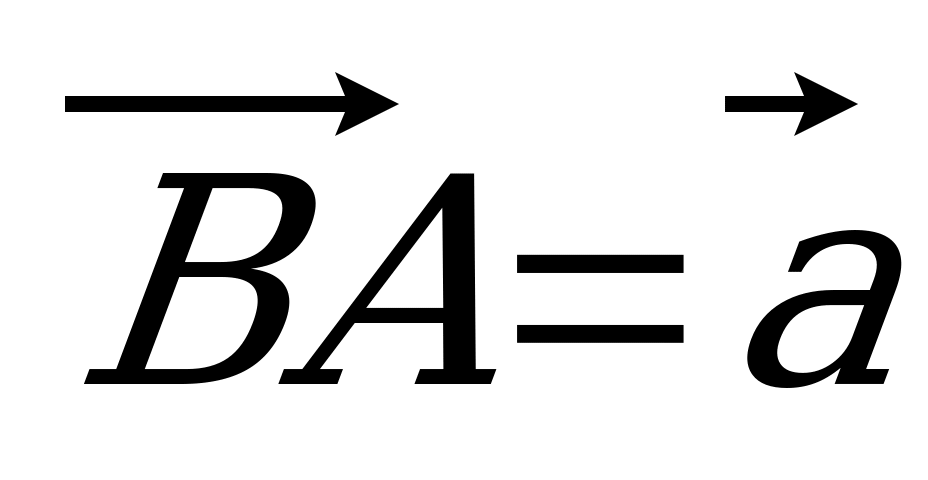 , , 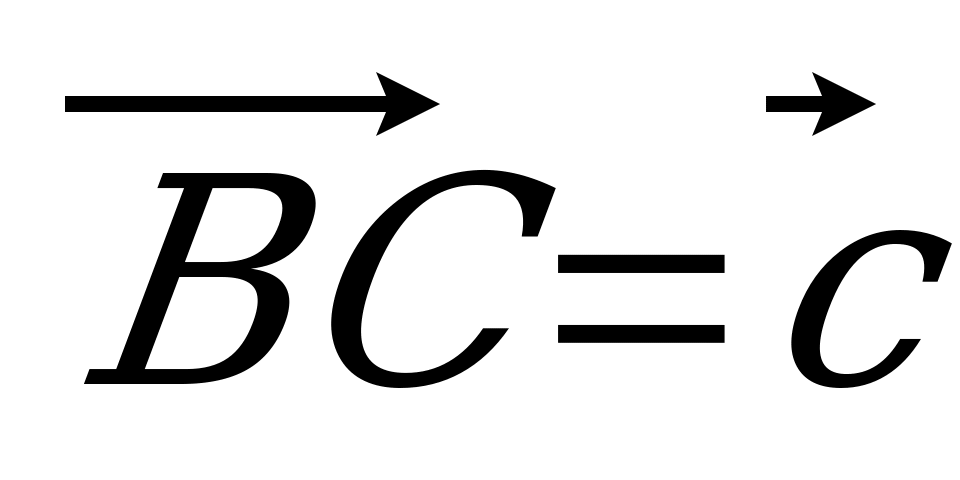 , , 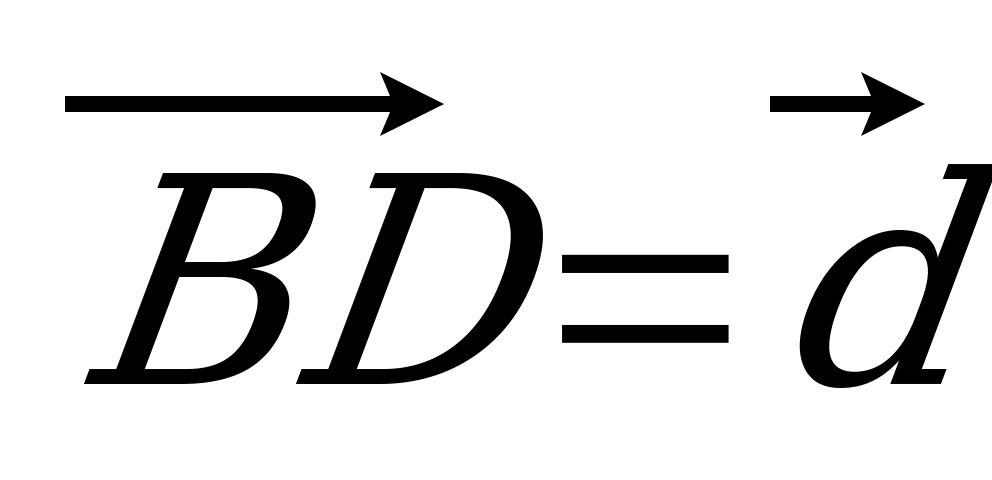 . . 3. Дан AMD, его медианы пересекаются в точке O, P – середина отрезка SO (точка S не лежит в плоскости AMD). Выразите 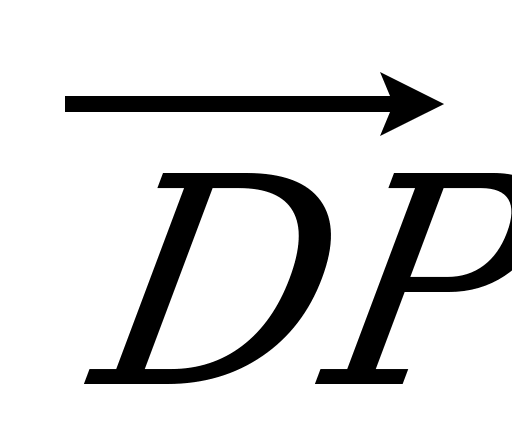 через векторы через векторы 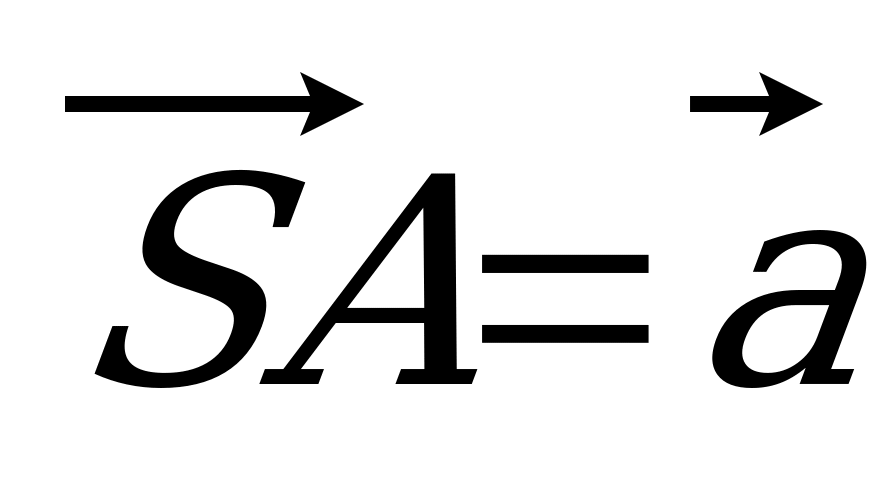 , , 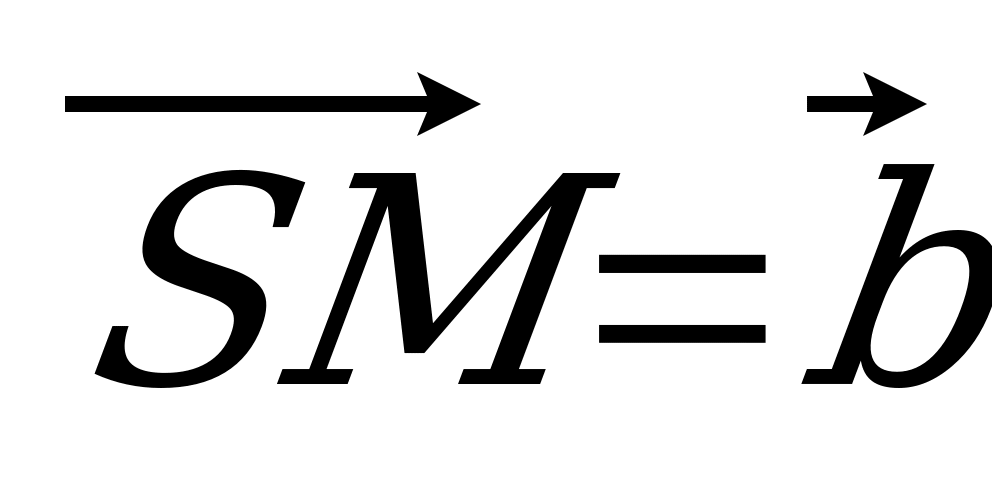 , , 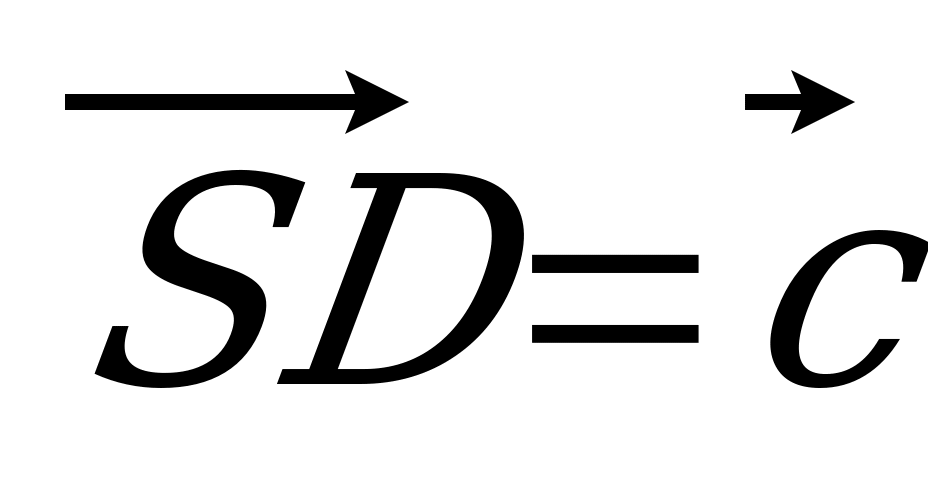 . . 4. ABCDA1B1C1D1 – параллелепипед. На C1A1 лежит точка N, причем C1N : NA1 = 2 : 5, а на C1C – М, причем C1М : МC =
= 3 : 1. Разложите вектор 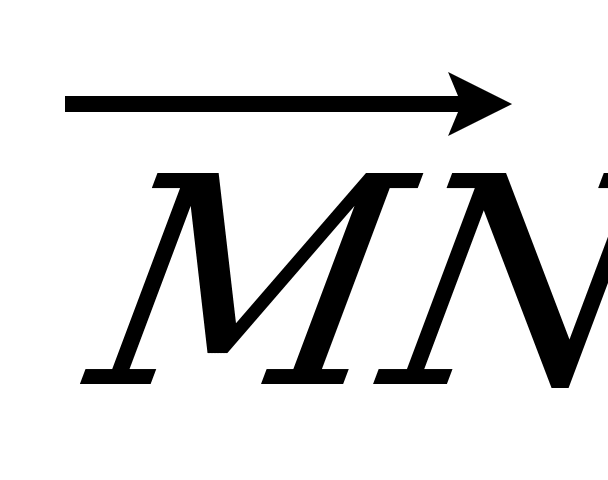 по векторам по векторам 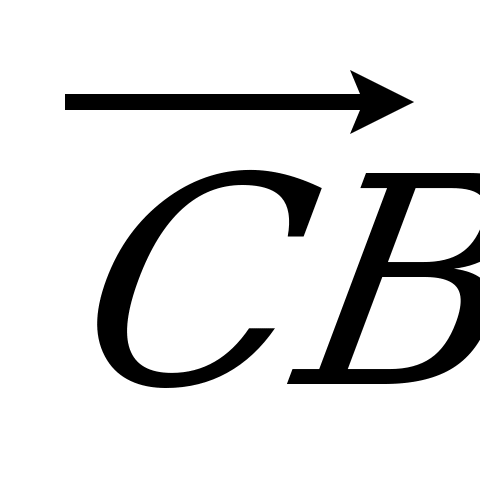 , ,  и и 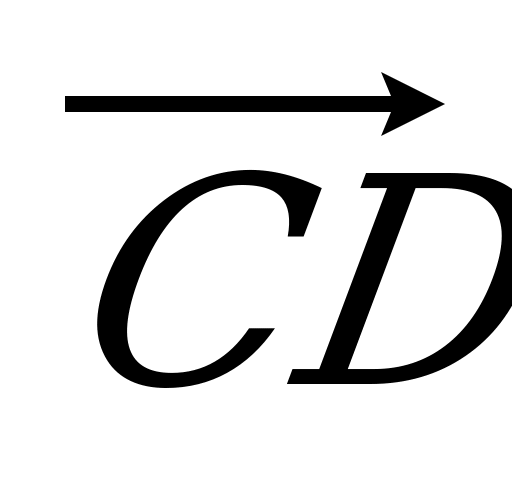 . . | Вариант 8 1. Дан параллелепипед ABCDA1B1C1D1. Укажите вектор с началом и концом в вершинах параллелепипеда, равный: 1) 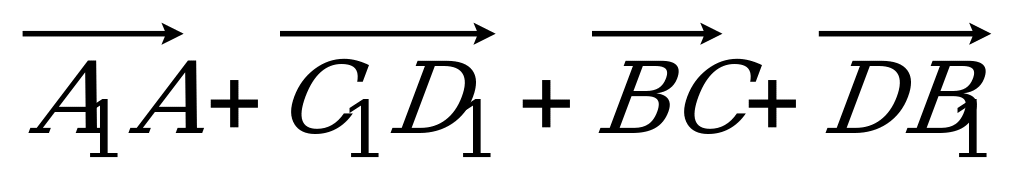 ; 2) ; 2) 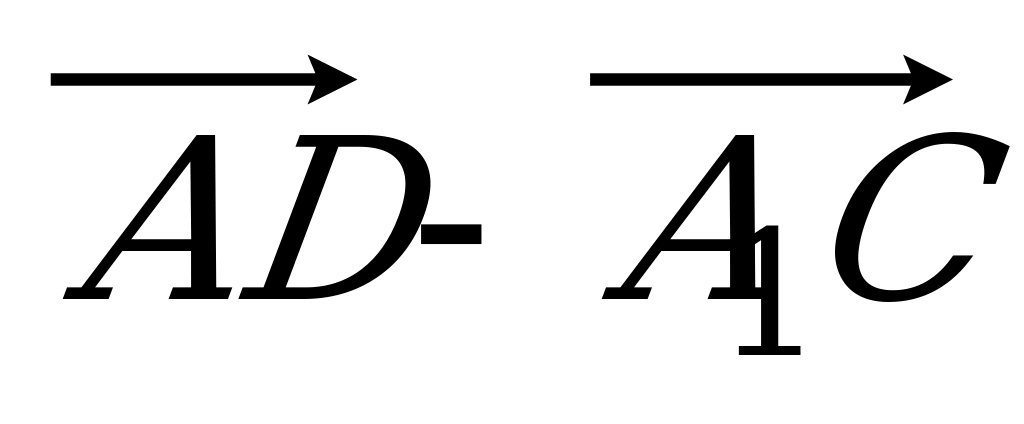 . . 2. Точка N – середина отрезка CK, соединяющего вершину С тетраэдра DABC с точкой K – серединой ребра AB. Разложите вектор  по векторам по векторам 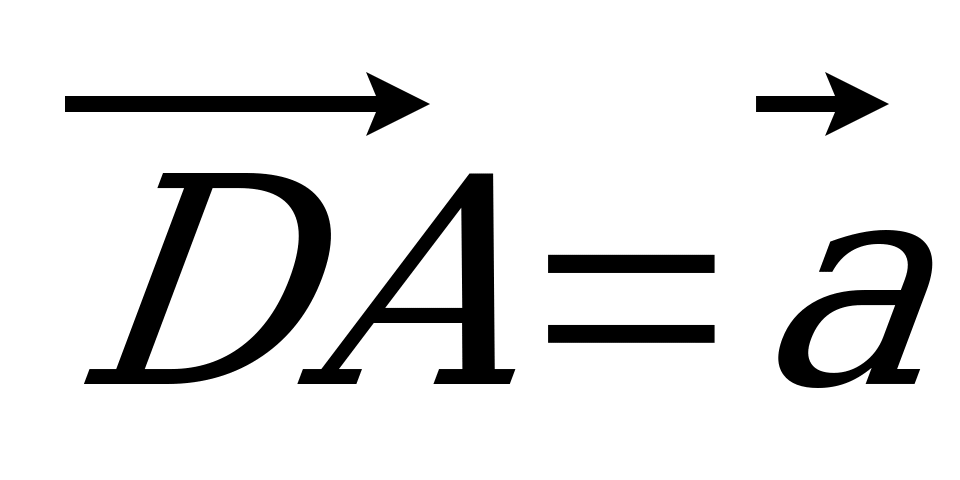 , , 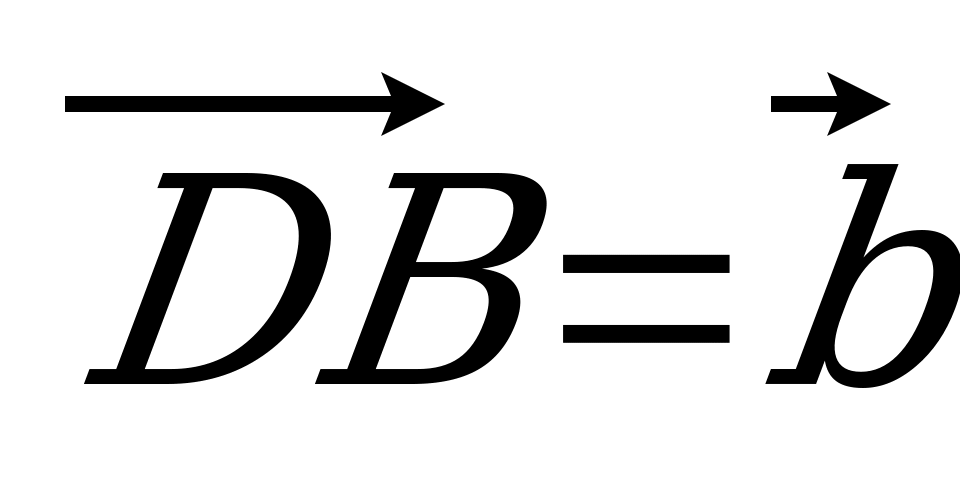 , , 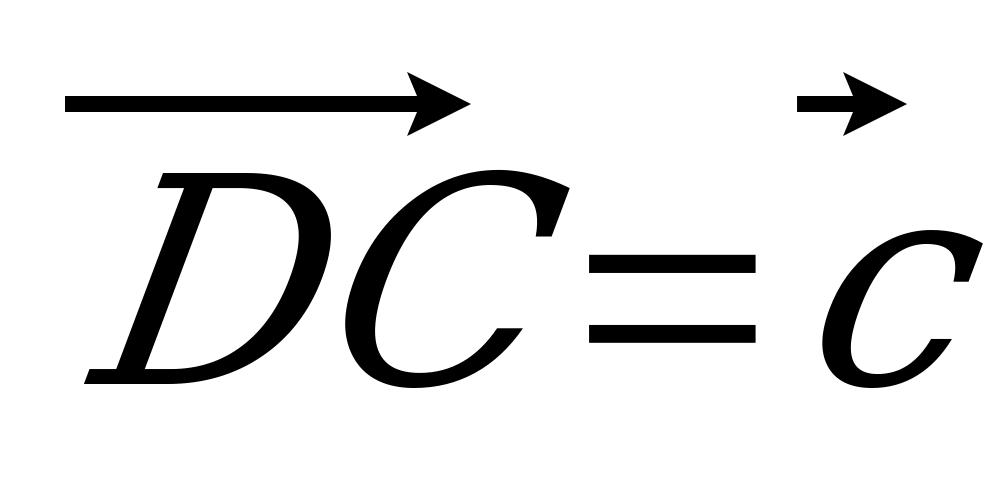 . . 3. Точка R – пересечение медиан грани DAB тетраэдра DABC, точка P – середина отрезка CR. Выразите вектор 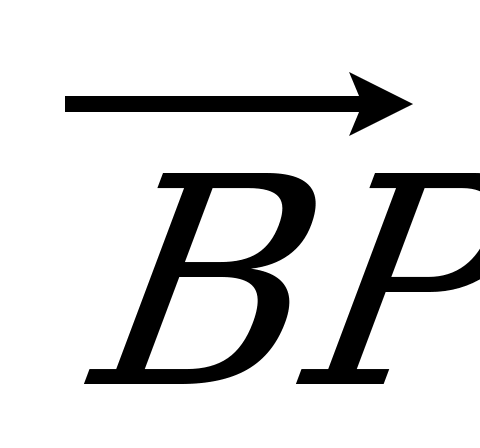 через векторы через векторы 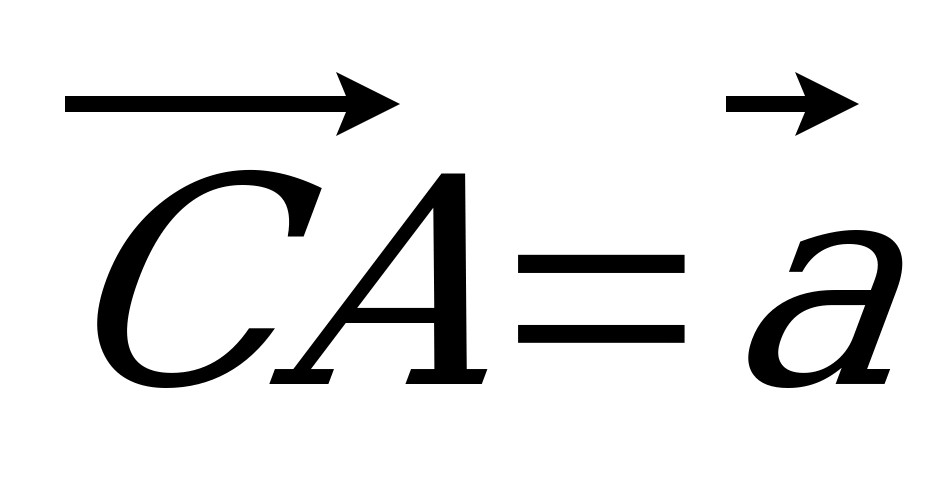 , , 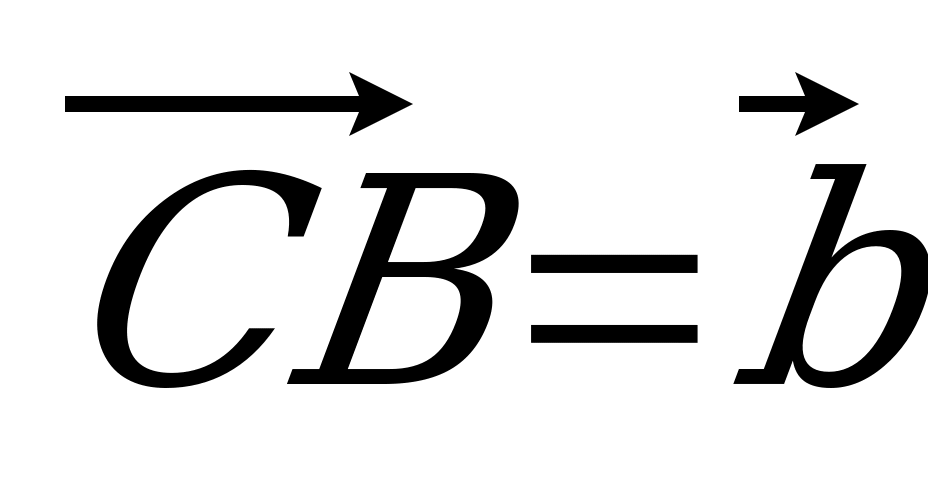 , , 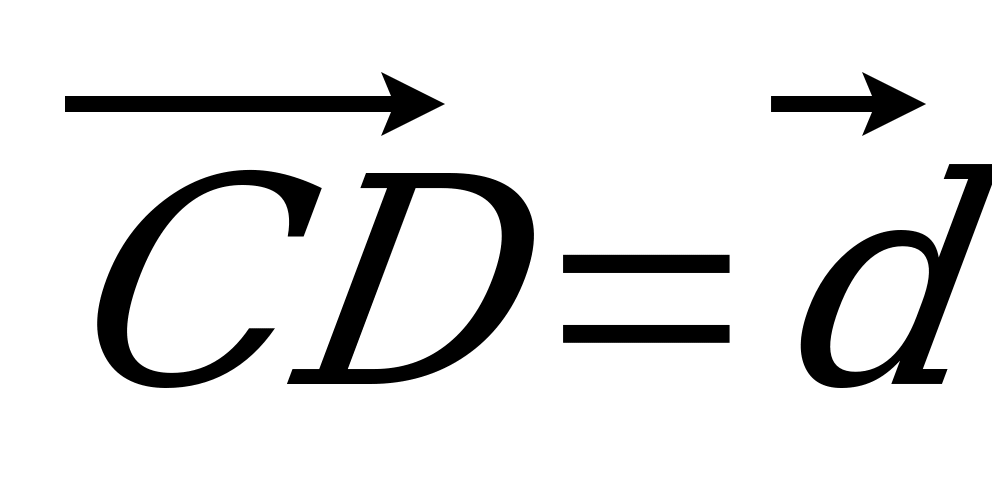 . . 4. В параллелепипеде ABCDA1B1C1D1 точка T лежит на B1С так, что B1T : TС = 3 : 2, точка O делит CD так, что СО : ОD =
= 4 : 1. Разложите вектор  по векторам по векторам 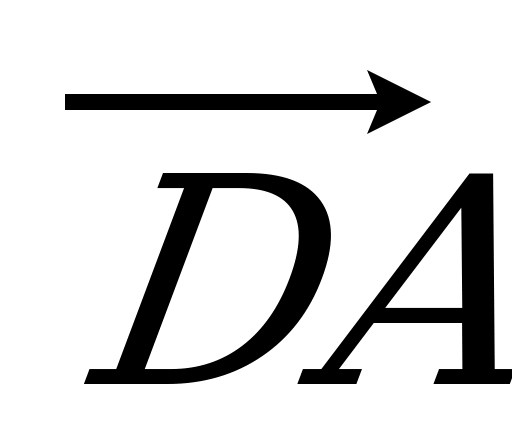 , ,  и и 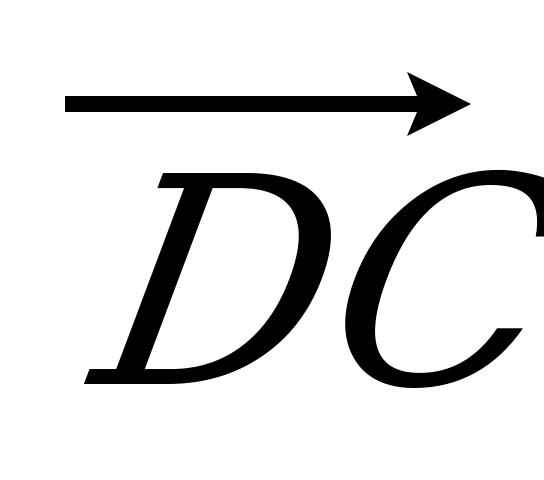 . . |

















