Муниципальное казенное образовательное учреждение
«Средняя общеобразовательная школа д. Шибково»
Искитимского района Новосибирской области
Рассмотрено Согласовано Утверждаю
на заседании МО учителей Зам. директора по УВР Директор МКОУ «СОШ д. Шибково»
___________________________ _______________ ______ _______________ ___________________________
___________________________
Протокол №___от «___» сентября 20___г. «___» сентября 20___г. «___» сентября 20___г.
Руководитель МО
____________ ___________________
Рабочая программа учебного курса
«Математика»
для__9__класса
Учитель: Татьяна Васильевна Лоенко
2015 – 2016 уч. год
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Рабочая программа по математике для учащихся 9 класса МКОУ СОШ «д.Шибково» составлена на основе Примерной программы основного общего образования, в соответствии с требованиями федерального компонента государственного стандарта общего образования и с авторской программой линии Ю.Н. Макарычева, К.И. Нешкова, Н.Г. Миндюка, С.Б. Суворовой, авторской программой линии Л.С. Атанасян.
Рабочая программа рассчитана на 170 часов за 1 год при недельной нагрузке 5 часов в неделю (на основании учебного плана МКОУ «СОШ д. Шибково», утвержденного приказом директора №35 от 24 августа 2015 года).
Для реализации рабочей программы используется учебник Алгебра (учебник для 9 класса общеобразовательных учреждений/ Ю.Н.Макарычев, К.И. Нешков, Н.Г. Миндюк, С.Б.Суворова; под ред.С.А.Теляковского. – М.: Просвещение, 2012), УМК Атанасяна Л.С. Геометрия 7-9 (Л.С. Атанасян, В.Ф. Бутузов, СВ. Кадомцев и др. Геометрия. 7—9 классы : учебник для общеобразоват. учреждений. 12-е изд. — М. : Просвещение, 2012. — 224 с. : ил.), включенные в федеральный перечень на данный учебный год (приказ МОН от 31 марта 2014 года № 253, внесенными приказом Минобрнауки России от 8 июня 2015 г. №576).
Целью изучения курса «Математика» в 9 кл. является развитие вычислительных и формально оперативных алгебраических умений учащихся до уровня, позволяющего уверенно их использовать при решении задач математики и смежных предметов (физики, химии, информатики ит.д.); усвоение аппарата уравнений как основного средства моделирования прикладных задач; систематическое изучение свойств геометрических фигур на плоскости, формирование пространственных представлений, развитие логического мышления и подготовка аппарата, необходимого для изучения смежных дисциплин (физика, черчение) и курса стереометрии в старших классах, осуществление функциональной подготовки школьников.
Курс характеризуется повышением теоретического уровня обучения, постепенным усилением роли теоретических обобщений. Прикладная направленность курса обеспечивается систематическим обращением к примерам, раскрывающим возможности применения математики к изучению действительности и решению практических задач. Практическая направленность курса выражается в целенаправленном развитии необходимого математического аппарата.
Цели обучения математики в общеобразовательной школе определяются ее ролью в развитии общества в целом и формировании личности каждого отдельного человека.
В задачи обучения математики входит:
овладение системой математических знаний и умений, необходимых для применения практической деятельности изучения смежных дисциплин, продолжения образования;
овладение навыками дедуктивных рассуждений;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, необходимой, в частности, для освоения курса информатики;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и т.д.);
воспитание культуры личности, отношения к математике как части общечеловеческой культуры, понимание значимости математики для научно технического прогресса;
развитие представлений о полной картине мира, о взаимосвязи математики с другими предметами.
Курс алгебры построен в соответствии с традиционными содержательно-методическими линиями:
В курсе алгебры 9-го класса продолжается систематизация и расширение сведений о функциях. Важное место занимает изучение квадратичных функций и их свойств, а также частных видов: �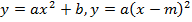 �. Формируются умения решать неравенства вида: �
�. Формируются умения решать неравенства вида: �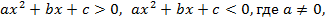 � которые опираются на сведения о графике квадратичной функции. На этапе 9-го класса завершается изучение рациональных уравнений с одной переменной. Дается понятие целого рационального уравнения и его степени. Особое внимание уделяется решению уравнений третьей и четвертой степени с помощью разложения на множители и введения вспомогательной переменной, что широко используется в дальнейшем при решении тригонометрических, логарифмических и других видов уравнений. Рассматриваются системы, содержащие уравнения второй степени с двумя неизвестными. Даются первые знания об арифметической и геометрической прогрессиях, как о частных видах последовательностей. Изучая формулу нахождения суммы �
� которые опираются на сведения о графике квадратичной функции. На этапе 9-го класса завершается изучение рациональных уравнений с одной переменной. Дается понятие целого рационального уравнения и его степени. Особое внимание уделяется решению уравнений третьей и четвертой степени с помощью разложения на множители и введения вспомогательной переменной, что широко используется в дальнейшем при решении тригонометрических, логарифмических и других видов уравнений. Рассматриваются системы, содержащие уравнения второй степени с двумя неизвестными. Даются первые знания об арифметической и геометрической прогрессиях, как о частных видах последовательностей. Изучая формулу нахождения суммы �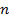 � первых членов арифметической прогрессии �
� первых членов арифметической прогрессии �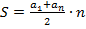 � и формулу суммы �
� и формулу суммы �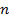 � первых членов геометрической прогрессии �
� первых членов геометрической прогрессии �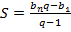 �, целесообразно уделить внимание заданиям, связанным с непосредственным применением этих формул.
�, целесообразно уделить внимание заданиям, связанным с непосредственным применением этих формул.
Для более широкого и глубокого знакомства с математикой введен курс «Элементы статистики и теории вероятностей» в количестве 10 часов. На этом этапе продолжается решение задач путем перебора возможных вариантов, изучается статистический подход к понятию вероятности. Формируются умения вычислять вероятности с помощью формул комбинаторики. Особое внимание уделяется правилу сложения и умножения вероятностей.
В курсе геометрии 9-го класса особое внимание уделяется применению подобия треугольников к доказательствам теорем и решению задач. Учащиеся дополняют знания о треугольниках сведениями о методах вычисления элементов произвольных треугольниках, основанных на теоремах синусов и косинусов. Даются систематизированные сведения о правильных многоугольниках, об окружности, вписанной в правильный многоугольник и описанной. Особое место занимает решение задач на применение формул. Формируются практические навыки вычисления площадей многоугольников в ходе решения задач. Серьезное внимание уделяется формированию умений рассуждать, делать простые доказательства, давать обоснования выполняемых действий. Параллельно закладываются основы для изучения систематических курсов стереометрии, физики, химии и других смежных предметов.
В рабочую программу внесены следующие изменения по сравнению с Примерной программой:
| №№ | тема | Количество часов по программе | Количество часов по модифицир. программе |
| алгебра |
| 1. | Квадратичная функция. | 24 | 25 |
| 2. | Уравнения и системы уравнений. | 18 | 20 |
| 3. | Прогрессии. | 14 | 14 |
| 4. | Степень с дробным показателем. | 9 | 9 |
| 5. | Элементы статистики и теории вероятностей | 13 | 13 |
| 6. | Повторение. Решение задач. | 25 | 21 |
Рабочая программа по геометрии соответствует Примерной программой:
| № п/п | тема | Количество часов по программе |
| 1. | Повторение | 2 |
| 2. | Векторы | 12 |
| 3 | Метод координат | 10 |
| 4 | Соотношения между сторонами и углами треугольника. Скалярное произведение векторов. | 14 |
| 5 | Длина окружности и площадь круга. | 12 |
| 6 | Движение | 10 |
| 7 | Обобщающее повторение курса геометрии. | 8 |
Программой отводится на изучение алгебры по 3 урока в неделю, что составляет 102 часа в учебный год. Из них контрольных работ 10 часов, которые распределены по разделам следующим образом:
«Квадратичная функция» -2 час,
«Уравнения и системы уравнений» -1 час,
«Арифметическая и геометрическая прогрессии» - 2 часа,
«Корень n-ой степени» -1 час
«Элементы статистики и теории вероятностей» -1час
Итоговый тест -2 часа
Программой отводится на изучение геометрии по 2 урока в неделю, что составляет 68 часов в учебный год. Из них контрольных работ 5 часов, которые распределены по разделам следующим образом:
«Подобие фигур» -1 час,
«Решение треугольников» -1 час,
«Многоугольники» - 1 час,
«Площади фигур» - 1час,
Итоговый тест – 1час.
Данное планирование определяет достаточный объем учебного времени для повышения математических знаний учащихся в среднем звене школы, улучшения усвоения других учебных предметов. Количество часов по темам изменено в связи со сложностью тем. Промежуточная аттестация проводится в форме тестов, самостоятельных, проверочных работ и математических диктантов (по 10 - 15 минут) в конце логически законченных блоков учебного материала. Итоговая аттестация предусмотрена в виде теста, приближенного к форме ОГЭ.
Оценка качества образования происходит по пятибалльной системе в соответствии с существующими нормами оценки знаний, умений и навыков учащихся с учетом их индивидуальных особенностей.
1. Содержание и объем материала, подлежащего проверке, определяется программой. При проверке усвоения материала нужно выявлять полноту, прочность усвоения учащимися теории и умения применять ее на практике в знакомых и незнакомых ситуациях.
2. Основными формами проверки знаний и умений учащихся по математике являются письменная контрольная работа и устный опрос.
При оценке письменных и устных ответов учитель в первую очередь учитывает показанные учащимися знания и умения. Оценка зависит также от наличия и характера погрешностей, допущенных учащимися.
3. Среди погрешностей выделяются ошибки и недочеты. Погрешность считается ошибкой, если она свидетельствует о том, что ученик не овладел основными знаниями, умениями, указанными в программе.
К недочетам относятся погрешности, свидетельствующие о недостаточно полном или недостаточно прочном усвоении основных знаний и умений или об отсутствии знаний, не считающихся в программе основными. Недочетами также считаются: погрешности, которые не привели к искажению смысла полученного учеником задания или способа его выполнения; неаккуратная запись; небрежное выполнение чертежа.
Граница между ошибками и недочетами является в некоторой степени условной. При одних обстоятельствах допущенная учащимися погрешность может рассматриваться учителем как ошибка, в другое время и при других обстоятельствах — как недочет.
4. Задания для устного и письменного опроса учащихся состоят из теоретических вопросов и задач.
Ответ на теоретический вопрос считается безупречным, если по своему содержанию полностью соответствует вопросу, содержит все необходимые теоретические факты я обоснованные выводы, а его изложение и письменная запись математически грамотны и отличаются последовательностью и аккуратностью.
Решение задачи считается безупречным, если правильно выбран способ решения, само решение сопровождается необходимыми объяснениями, верно выполнены нужные вычисления и преобразования, получен верный ответ, последовательно и аккуратно за писано решение.
5. Оценка ответа учащегося при устном и письменном опросе проводится по пятибалльной системе, т. е. за ответ выставляется одна из отметок: 1 (плохо), 2 (неудовлетворительно), 3 (удовлетворительно), 4 (хорошо), 5 (отлично).
6. Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельству ют о высоком математическом развитии учащегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные учащемуся дополнительно после выполнения им заданий.
Критерии ошибок:
К г р у б ы м ошибкам относятся ошибки, которые обнаруживают незнание учащимися формул, правил, основных свойств, теорем и неумение их применять; незнание приемов решения задач, рассматриваемых в учебниках, а также вычислительные ошибки, если они не являются опиской;
К н е г р у б ы м ошибкам относятся: потеря корня или сохранение в ответе постороннего корня; отбрасывание без объяснений одного из них и равнозначные им;
К н е д о ч е т а м относятся: нерациональное решение, описки, недостаточность или отсутствие пояснений, обоснований в решениях.
Оценка устных ответов учащихся по математике
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотрен ном программой и учебником,
изложил материал грамотным языком в определенной логической последовательности, точно используя математическую терминологию и символику;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теоретические положения конкретными примерами, применять их в новой ситуации при выполнении практического задания;
продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость используемых при от работке умений и навыков;
отвечал самостоятельно без наводящих вопросов учителя. Возможны одна - две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию учителя.
Ответ оценивается отметкой «4», если он удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившие математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные по замечанию учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные по замечанию учителя.
Отметка «3» ставится в следующих случаях:
неполно или непоследовательно раскрыто содержание материала, но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала (определенные «Требованиями к математической подготовке учащихся»);
имелись затруднения или допущены ошибки в определении понятий, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изучаемому материалу.
Оценка письменных контрольных работ учащихся по математике
Отметка «5» ставится, если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала).
Отметка «4» ставится, если:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущена одна ошибка или два-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущены более одной ошибки или более двух-трех недочетов в выкладках, чертежах или графиках, но учащийся владеет обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что учащийся не владеет обязательными умениями по данной теме в полной мере
Отметка «1» ставится, если:
работа показала полное отсутствие у учащегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.
Домашнее задание описано на блок уроков. По ходу работы, в зависимости от темпа прохождение материала номера заданий распределяются по урокам так, что по окончании изучения блока все задания выполнены учащимися в обязательном порядке. Некоторые уроки проводятся совместно с информатикой, используя УМК Живая математика.
Требования к уровню подготовки учащихся.
В результате изучения курса алгебры 9-го класса учащиеся должны уметь:
строить график квадратичной функции; находить по графику промежутки возрастания и убывания функции, а также промежутки, в которых функция сохраняет знак;
понимать содержательный смысл важнейших свойств функции; по графику функции отвечать на вопросы, касающиеся её свойств;
бегло и уверенно выполнять арифметические действия с рациональными числами; вычислять значения числовых выражений, содержащих степени и корни;
решать простейшие системы, содержащие уравнения второй степени с двумя переменными; решать текстовые задачи с помощью составления таких систем;
решать квадратные уравнения и уравнения, сводящиеся к ним, используя приемы и формулы для решения различных видов квадратных уравнений, графический способ решения уравнений;
распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
вычислять значения тригонометрических функций по известному значению одной из них; выполнять несложные преобразования тригонометрических выражений;
пользоваться геометрическим языком для описания предметов окружающего мира;
распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразование фигур;
вычислять значения геометрических величин (длин, углов, площадей), в том числе: определять значение тригонометрических функций по заданным значениям углов;
находить стороны, углы и площади треугольников, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;
решать геометрические задания, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, соображения симметрии;
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
решать простейшие планиметрические задачи в пространстве.
использовать приобретенные знания, умения, навыки в практической деятельности и повседневной жизни для:
решения несложных практических расчетных задач, в том числе с использованием при необходимости справочной литературы, калькулятора, компьютера;
устной прикидки, и оценки результата вычислений, проверки результата вычислений выполнением обратных действий;
интерпретации результата решения задач.
Содержание обучения
Действительные числа. Корень третьей степени.
Алгебраические выражения. Квадратный трёхчлен; разложение квадратного трёхчлена на множители.
Уравнения. Равносильность уравнений. Решение уравнений, сводящихся к линейным и квадратным. Примеры решения уравнений третьей и четвёртой степеней.
Уравнение с двумя переменными. Линейное уравнение с двумя переменными, примеры решения уравнений в целых числах.
Система уравнений с двумя переменными. Равносильность систем. Системы двух линейных уравнений с двумя переменными; решение подстановкой и сложением. Примеры решения систем нелинейных уравнений с двумя переменными.
Решение текстовых задач алгебраическим способом.
Декартовы координаты на плоскости. Графическая интерпретация уравнения с двумя переменными. Графики простейших нелинейных уравнений: парабола, гипербола, окружность. Графическая интерпретация систем уравнений с двумя переменными.
Неравенства. Квадратные неравенства. Системы неравенств с одной переменной.
Функции. Зависимости между величинами. Примеры графиков зависимостей, отражающих реальные процессы.
Числовые функции. Понятие функции, область применения и область значения функции. Способы задания функции. График функции. Свойства функции, их отражение на графике. Квадратичная функция, её график и свойства.
Степенные функции с натуральными показателями 2 и 3, их графики и свойства.
Числовые последовательности. Понятие числовой последовательности. Задание последовательности рекуррентной формулой и формулой n-го члена. Арифметическая и геометрическая прогрессии. Формулы n-го члена арифметической и геометрической прогрессий, суммы первых п-х членов.
Изображение членов арифметической и геометрической прогрессий точками координатной плоскости. Линейный и экспоненциальный рост. Сложные проценты.
Случайные события и вероятность. Понятие о случайном опыте и случайном событии. Частота случайного события. Статистический подход к понятию вероятности. Вероятности противоположных событий. Достоверные и невозможные события. Равновозможность событий. Классическое определение вероятности.
Комбинаторика. Решение комбинаторных задач перебором вариантов. Комбинаторное правило умножения. Перестановки и факториал.
Векторы. Геометрические фигуры и их свойства. Измерение геометрических величин. Вектор. Длина (модуль) вектора. Равенство векторов. Операции над векторами: умножение вектора на число, сложение, разложение. Применение векторов к решению задач.
Метод координат. Геометрические фигуры и их свойства. Измерение геометрических величин.
Вектор. Длина (модуль) вектора. Равенство векторов. Координаты вектора. Операции над векторами: умножение вектора на число, сложение, разложение по двум неколлинеарным векторам.
Простейшие задачи в координатах. Уравнение окружности. Уравнение прямой.
Соотношения между сторонами и углами треугольника. Скалярное произведение векторов. Геометрические фигуры и их свойства. Измерение геометрических величин.
Синус, косинус и тангенс углов от 0о до 180о. Угол между векторами. Теорема синусов и теорема косинусов. Примеры их применения для вычисления элементов треугольника.
Формула, выражающая площадь треугольника через две стороны и угол между ними. Скалярное произведение векторов.
Длина окружности и площадь круга. Геометрические фигуры и их свойства. Измерение геометрических величин.
Вписанные и описанные многоугольники. Правильные многоугольники. Сумма углов правильного многоугольника.
Длина окружности, число π; длина дуги. Площадь круга и площадь сектора.
Вписанные и описанные окружности правильного многоугольника
Движение. Геометрические преобразования. Геометрические фигуры и их свойства.
Примеры движений фигур. Симметрия фигур. Осевая симметрия и параллельный перенос. Поворот и центральная симметрия (материал подлежит изучению, но не включается в Требования к уровню подготовки учеников).
Итоговое повторение.
Решение задач
Сокращения, используемые в рабочей программе:
Типы уроков:
УОНМ — урок ознакомления с новым материалом.
УЗИМ — урок закрепления изученного материала.
УПЗУ — урок применения знаний и умений.
УОСЗ — урок обобщения и систематизации знаний.
УПКЗУ — урок проверки и коррекции знаний и умений.
КУ — комбинированный урок.
Виды контроля:
ФО — фронтальный опрос.
ИРД — индивидуальная работа у доски.
ИРК — индивидуальная работа по карточкам.
СР — самостоятельная работа.
ПР — проверочная работа.
МД — математический диктант.
Т – тестовая работа.
Методическое обеспечение:
Макарычев Ю.Н. Алгебра, 9 класс: учебник для общеобразоват. Учреждений / Ю.Н.Макарычев, К.И.Нешков, Н.Г.Миндюк, С.Б. Суворова; под ред. С.А.Теляковского. – М.: Просвещение, 2012
Миндюк М.Б. Алгебра: рабочая тетрадь для 9 класса / М.Б.Миндюк, Н.Г.Миндюк. – М.: Издательский дом «Генжер», 2010
Жохов В.И. Уроки алгебры в 9 классе: кн. для учителя / В.И.Жохов, Л.Б. Крайнова. – М.: Просвещение,2009
Звавич Л.И. Дидактические материалы по алгебре. 9 класс / Л.И.Звавич, Л.В.Кузнецова, С.Б.Суворова. – М.: Просвещение, 2011
Атанасян Л.С., Геометрия. 7—9 классы : учебник для общеобразоват. учреждений. 10-е изд. — М. : Просвещение, 2011. — 224 с. : ил.
Гусев В. А., Медяник А. И. Дидактические материалы по геометрии для 9 класса.— 3-е изд., перераб.— М.: Просвещение, 1991.— 80 с.: ил.
Дудницын Ю.П. Геометрия. Рабочая тетрадь. 9 класс 8-е изд. - М., 2011. - 128 с.
Фарков А. Тесты и контрольные работы по геометрии. 9 класс: к учебнику Л.С.Ананасяна. - СПб.: Питер, 2011. — 128 с: ил.
Т.Л. Сытина, Ю.П. Дудницын. Раздаточный материал по геометрии для 9 класса. - М.: Просвещение, 1988 г.
Медяник А. И. Контрольные и проверочные работы по геометрии. 7—11 классы: Метод, пособие. — М.: Дрофа, 1997. — 144 с.
Геометрия. 9 класс: поурочные планы по учебнику Л.С.Ананасяна / авт.-сост. Е. П. Моисеева. - Волгоград: Учитель, 2006. - 122 с.
Контрольно-измерительные материалы,
используемые при оценке качества обучения.
9 класс, алгебра
| № п/п | алгебра | геометрия |
|
| Входной контроль. |
|
| 1 | Квадратичная функция | Векторы |
| 2 | Неравенства и уравнения | Метод координат |
| 3 | Решение систем уравнений второй степени | Соотношения между сторонами и углами треугольника |
| 4 | Арифметическая прогрессия | Длина окружности и площадь круга |
| 5 | Геометрическая прогрессия | Движение |
| 6 | Арифметический корень n-ой степени |
|
| 7 | Комбинаторные задачи |
|
| 8 | Итоговая контрольная работа |
|
КАЛЕНДАРНО – ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
9класс, алгебра
3 часа в неделю, всего 102
I четверть
27 уроков за четверть
| № урока | Содержание учебного материала | Примерные сроки изучения тем и проведения контрольных работ |
|
| Квадратичная функция (25 часов) | 01.09 – 27.10 |
| 1-2
3-4 5-6 7-8 9-10
11-12
13-16 17 18-21 22-25 | Функции и их графики. Область определения и область значений. Свойства функций. Квадратный трехчлен и его корни. Разложение квадратного трехчлена на множители. Функция �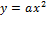 �. �. Графики функций �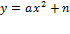 � и � � и �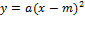 �. �. Построение графика квадратичной функции. Контрольная работа №1 Решение неравенств второй степени. Метод интервалов. |
08.10 |
|
| Уравнения и системы уравнений (20 часов) | 29.10 – 19.12 |
| 26-27 | Целое уравнение и его корни. |
|
II четверть
21 урок за четверть
| № урока | Содержание учебного материала | Примерные сроки |
|
| Уравнения и системы уравнений (окончание) |
|
| 28 29-32 33 34-36 37-40 41-44
45 | Равносильные уравнения. Уравнения, приводимые к квадратным. Контрольная работа № 2 Графический способ решения систем уравнений. Решение систем уравнений второй степени. Решение задач с помощью систем уравнений второй степени. Контрольная работа № 3 |
21.11
19.12 |
|
| Прогрессии (14 часов) | 22.12 – 04.02 |
| 46 47-48 | Последовательности. Определение арифметической прогрессии. |
|
III четверть
30 уроков за четверть
| № урока | Содержание учебного материала |
|
|
| Прогрессии (окончание) |
|
| 49-51
52 53-54 55-56
57-58
59 | Формула суммы n- первых членов арифметической прогрессии. Контрольная работа № 3 Геометрическая прогрессия. Формула суммы n первых членов геометрической прогрессии. Среднее геометрическое. Сумма бесконечно-убывающей геометрической прогрессии. Контрольная работа № 4 | 19.01
04.02 |
|
| Степень с рациональным показателем (9 часов) | 06.02 – 27.02 |
| 60-61
62-63 64-67 68 | Четные и нечетные функции. Свойства степенной функции. Определение корня n-степени и его свойства. Степень с рациональным показателем и ее свойства Контрольная работа № 5 |
27.02 |
|
| Элементы статистики и теории вероятностей (13 час) | 02.03-08.04 |
| 69-70 71-76 77-78 | Комбинаторные задачи. Перестановки. Размещения. Сочетания. Начальные сведения из теории вероятностей. |
|
IV четверть
24 урока за четверть
| № урока | Содержание учебного материала | Примерные сроки |
| | Элементы статистики и теории вероятностей (окончание) | |
| 79-80 81 | Сложение и умножение вероятностей. Контрольная работа №6 |
08.04 |
|
| Повторение (21час) | 10.04 – 22.05 |
| 82-102 | Итоговое повторение курса 5-6 класса Годовой тест |
|
9 класс, геометрия
2 часа в неделю, всего 68
I четверть
18 уроков за четверть
| № урока | Содержание учебного материала
| Примерные сроки изучения тем и проведения контрольных работ |
| 1-2 | Вводное повторение | 01.09-03.09 |
|
| Векторы (12часов) | 08.09 – 15.10 |
| 3-8
9-13
14 | Понятие вектора. Равенство векторов. Сумма двух векторов. Законы сложения векторов. Вычитание векторов Умножение вектора на число. Применение векторов к решению задач Контрольная работа № 1 |
15.10 |
|
| Метод координат (10 часов) | 20.10 – 26.11 |
| 15-18 | Разложение вектора по двум неколлинеарным векторам. Координаты вектора. Простейшие задачи в координатах |
|
II четверть
14 уроков за четверть
| № урока | Содержание учебного материала
| Примерные сроки |
| | Метод координат (продолжение) |
|
| 19-23
24
| Решение задач методом координат. Уравнение окружности. Уравнение прямой. Контрольная работа № 2 |
26.11
|
|
| Соотношения между сторонами и углами треугольника. Скалярное произведение векторов. (14 ч) | 01.12-26.01 |
| 25-27 28-30
31-32
| Синус, косинус, тангенс угла Теорема о площади треугольника. Теорема синусов. Теорема косинусов Решение треугольников. |
|
III четверть
20 уроков за четверть
| № урока | Содержание учебного материала | Примерные сроки |
| | Соотношения между сторонами и углами треугольника. Скалярное произведение векторов (окончание) | |
| 33-37
38 | Угол между векторами. Скалярное произведение векторов и его свойства. Контрольная работа № 3 |
26.01 |
|
| Длина окружности и площадь круга (12 часов) | 28.01-15.03 |
| 39-42
43-44 45-49 50 | Правильный многоугольник. Окружность, описанная около правильного многоугольника. Окружность, вписанная в правильный многоугольник. Длина окружности. Площадь круга и кругового сектора Контрольная работа № 4 |
15.03 |
|
| Движение (10 часов) | 17.09-26.04 |
| 51-52 | Отображение плоскости на себя. Понятие движения. Свойства движения |
|
IV четверть
16уроков за четверть
| № урока | Содержание учебного материала | Примерные сроки изучения тем |
|
| Движение (окончание) |
|
| 53-59 60 | Центральная и осевая симметрия. Параллельный перенос. Поворот Контрольная работа № 5 |
26.04 |
|
| Обобщающее повторение курса геометрии (8 часов) | 28.04-24.05 |
| 61-68 |
|
|

















