Рабочая программа по математике разработана на основе Федерального государственного образовательного стандарта среднего (полного) общего образования, Концепции духовно- нравственного развития и воспитания личности гражданина России, Фундаментального ядра содержания общего образования. Программа включает следующие разделы: пояснительную записку, общую характеристику учебного предмета, описание места учебного предмета в учебном плане, результаты изучения курса (личностные, метапредметные и предметные), содержание курса, примерное тематическое планирование с определением основных видов учебной деятельности обучающихся и описание материально-технического обеспечения образовательного процесса.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Базовый курс математики ориентирован на учащихся, ближайшее будущее которых не будет связано с изучением математики в высших учебных заведениях, поэтому материал изучается на общекультурном уровне. В программу курса включены важнейшие понятия, позволяющие построить логическое завершение школьного курса математики.
В программу курса включены важнейшие понятия, позволяющие построить логическое завершение школьного курса математики и создающие достаточную основу обучающимся для продолжения математического образования, а также для решения практических задач в повседневной жизни.
Обучение математике является важнейшей составляющей среднего (полного) общего образования и призвано развивать логическое мышление учащихся, обеспечить овладение учащимися умениями в решении различных практических и межпредметных задач. Математика входит в предметную область «Математика и информатика».
Изучение курса математики 10 классе в соответствии с Федеральным образовательным стандартом среднего (полного) общего образования должно обеспечить сформированность: «представлений о социальных, культурных и исторических факторах становления математики; основ логического, алгоритмического и математического мышления; умений применять полученные знания при решении различных задач; представлений о математике как части общечеловеческой культуры, универсальном языке науки, позволяющем описывать и изучать реальные процессы и явления» .
При разработке учебников авторы дополнительно ставили перед собой следующие цели: развитие личности школьника средствами математики, подготовка его к продолжению обучения и к самореализации в современном обществе.
Достижение перечисленных целей предполагает решение следующих задач:
— формирование мотивации изучения математики, готовности и способности учащихся к саморазвитию, личностному самоопределению, построению индивидуальной траектории в изучении предмета;
— формирование у учащихся способности к организации своей учебной деятельности посредством освоения личностных, познавательных, регулятивных и коммуникативных универсальных учебных действий;
— формирование специфических для математики стилей мышления, необходимых для полноценного функционирования в современном обществе, в частности логического, алгоритмического и эвристического;
— освоение в ходе изучения математики специфических видов деятельности, таких как построение математических моделей, выполнение инструментальных вычислений, овладение символическим языком предмета и др.;
— формирование умений представлять информацию в зависимости от поставленных задач в виде таблицы, схемы, графика, диаграммы, использовать компьютерные программы и Интернет при ее обработке;
— овладение учащимися математическим языком и аппаратом как средством описания и исследования явлений окружающего мира;
— овладение системой математических знаний, умений и навыков, необходимых для решения задач повседневной жизни, изучения смежных дисциплин и продолжения образования;
— формирование научного мировоззрения;
— воспитание отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
Содержание курса математики строится на основе системно-деятельностного подхода, принципов разделения трудностей, укрупнения дидактических единиц, опережающего формирования ориентировочной основы действий, принципов позитивной
педагогики.
ОБЩАЯ ХАРАКТЕРИСТИКА УЧЕБНОГО ПРЕДМЕТА
Курс математики 10 класса базового уровня делится на два предмета: алгебра и начала математического анализа и геометрия. Курс алгебры и начал математического анализа включает в себя следующие содержательные линии: числа и числовые выражения, тождественные преобразования, уравнения и неравенства, функции, вероятность и статистика, логика и множество, математика в историческом развитии.
В своей совокупности они учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале.
Раздел «Числа и числовые выражения» призван способствовать приобретению практических навыков вычислений, необходимых для повседневной жизни и изучения других предметов. Он также служит базой для дальнейшего изучения математики, способствует развитию логического мышления и формирования умения пользоваться вычислительными алгоритмами. Развитие понятия о числе в старшей школе связано с изучением иррациональных чисел, формированием представлений о действительных и комплексных числах.
Раздел «Тождественные преобразования» нацелен на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Одними из основных задач изучения этого раздела являются развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики, и овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Учащиеся осуществляют тождественные преобразования показательных, логарифмических, тригонометрических выражений, что находит применение в решении соответствующих уравнений, неравенств и их систем.
Раздел «Уравнения и неравенства» продолжает алгебраическую линию курса основной школы, перенося основные алгебраические приемы решения уравнений, неравенств и их систем в сферу иррациональных и трансцендентных выражений.
Особая роль в этом разделе принадлежит заданиям с параметрами, которые требуют от школьников умений находить нестандартные пути их решений.
Важной задачей раздела «Функции» является получение школьниками конкретных знаний о функциях как математических моделях для описания и исследования разнообразных процессов, для формирования у учащихся представлений о роли математики в развитии цивилизации. Изучение этого материала способствует освоению символическим и графическим языками, умению работать с таблицами.
Раздел «Вероятность и статистика» является компонентом школьного математического образования, усиливающим его прикладное значение. Этот материал необходим, прежде всего, для формирования функциональной грамотности — умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты. Формулы комбинаторики позволяют учащимся осуществлять рассмотрение разных случаев, перебор и подсчет числа вариантов, в том числе в простейших прикладных задачах.
При изучении статистики и теории вероятностей обогащаются представления школьников о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы стохастического мышления.
Раздел «Логика и множества» служит цели овладения учащимися элементами математической логики и теории множеств, что вносит важный вклад в развитие мышления и математического языка.
Раздел «Математика в историческом развитии» способствует повышению общекультурного уровня школьников, пониманию роли математики в общечеловеческой культуре, развитии цивилизации и современного общества. Время на изучение этого
раздела дополнительно не выделяется, усвоение его не контролируется, хотя исторические аспекты вплетаются в основной материал всех разделов курса.
МЕСТО ПРЕДМЕТА В УЧЕБНОМ ПЛАНЕ
В учебном плане на изучение алгебры и начал математического анализа на базовом уровне отводится 3 ч в неделю (35 недель), 105 ч в год.
СОДЕРЖАНИЕ УЧЕБНОГО ПРЕДМЕТА
ЧИСЛА И ЧИСЛОВЫЕ ВЫРАЖЕНИЯ
Корень степени n 1 и его свойства. Степень с рациональным показателем и ее свойства. Понятие о степени с действительным показателем.
Понятие логарифма числа. Десятичный и натуральный логарифмы, число е. Вычисление десятичных и натуральных логарифмов на калькуляторе. Роль логарифмов в расширении практических возможностей естественных наук.
Радианная мера угла. Синус, косинус, тангенс и котангенс числа. Арксинус, арккосинус, арктангенс, арккотангенс числа.
ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ
Многочлен с одной переменной. Делимость многочленов. Целые корни многочлена с целыми коэффициентами. Решение целого алгебраического уравнения. Основная теорема алгебры (без доказательства). Число корней многочлена. Бином Ньютона.
Свойства корней, степеней и логарифмов. Преобразования простейших выражений, содержащих корни, степени и логарифмы.
Основные тригонометрические тождества. Формулы приведения. Преобразования тригонометрических выражений. Синус, косинус и тангенс суммы и разности двух углов. Тригонометрические функции двойного угла. Преобразования сумм тригонометрических функций в произведение и обратные преобразования. Выражение тригонометрических функций через тангенс половинного аргумента. Преобразования выражений, содержащих обратные тригонометрические функции.
УРАВНЕНИЯ И НЕРАВЕНСТВА
Решение рациональных, иррациональных, показательных, логарифмических, тригонометрических уравнений и неравенств, а также их систем.
Основные приемы решения систем уравнений: подстановка, сложение, введение новых переменных. Равносильность уравнений, неравенств и систем. Решение системы уравнений с двумя неизвестными. Решение системы неравенств с одной неизвестной.
Использование свойств и графиков функций при решении уравнений и неравенств. Метод интервалов. Изображение на координатной плоскости множества решений уравнений, неравенств.
Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений.
ФУНКЦИИ
Понятие функции. Область определения и область значений. График функции. Построение графиков функций, заданных различными способами. Свойства функций: монотонность, четность и нечетность, периодичность.
Преобразования графиков: сдвиг и растяжение вдоль осей координат, симметрия относительно осей координат, начала координат и прямой y = x.
Линейная и квадратичная функции, функция y = 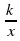 , их свойства и графики. График дробно-линейной функции. Степенная функция с натуральным показателем, функция y =
, их свойства и графики. График дробно-линейной функции. Степенная функция с натуральным показателем, функция y = 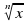 , их свойства и графики.
, их свойства и графики.
Тригонометрические функции, их свойства и графики. Обратные тригонометрические функции, их свойства и графики.
Показательная и логарифмическая функции, их свойства и графики.
ВЕРОЯТНОСТЬ И СТАТИСТИКА
Представление данных, их числовые характеристики. Таблицы и диаграммы. Случайный выбор. Интерпретация статистических данных и их характеристик. Случайные события и вероятность. Вычисление вероятностей. Перебор вариантов и элементы комбинаторики (формулы числа перестановок, размещений и сочетаний элементов).
МАТЕМАТИКА В ИСТОРИЧЕСКОМ РАЗВИТИИ
История развития понятия числа: комплексные числа, корни n-й степени. История вопроса о нахождении формул корней алгебраических уравнений. Формулы Кардано. Основная теорема алгебры. История развития алгебры: Н. Абель, Э. Безу, К. Гаусс, У. Горнер, Н. Тарталья, П. Ферма, С. Ферро. История вопроса о нахождении комплексных корней квадратных и кубических уравнений: Дж. Кардано, А. Муавр. Неразрешимость в радикалах уравнений степени, большей четырех.
История развития математического анализа: Л. Коши, Л. Кронекер, И. Кеплер, И. Ньютон, Г. Лейбниц. История развития логарифмов и логарифмических таблиц: И. Бюрги, Д. Непер, Г. Бригс, А. Влакк. Развитие математической логики:
Ч. Пирс, Ф. Фриге, Дж. Венн.
История развития теории вероятностей и статистики: П. Ферма, Х. Гюйгенс, Я. Бернулли, П. Лаплас, П. Л. Чебышев, И. Ньютон.
УЧЕБНО-ТЕМАТИЧЕСКИЙ ПЛАН
|
Содержание материала
| Количество часов |
| Глава 1. Функции и графики | 17 |
| 1. Понятие функции | 3 |
| 2. Прямая, гипербола, парабола и окружность | 4 |
| 3. Непрерывность и монотонность функций | 4 |
| 4. Квадратичная и дробно-линейная функции. Преобразование графиков | 5 |
| Зачет или контрольная работа № 1 | 1 |
| Глава 2. Степени и корни | 14 |
| 5. Степенная функция y = xn при натуральном значении n | 2 |
| 6. Понятие корня n-й степени | 4 |
| 7. Свойства арифметических корней | 4 |
| 8. Степень с рациональным показателем | 3 |
| Зачет или контрольная работа № 2 | 1 |
| Глава 3. Показательная и логарифмическая функции | 17 |
| 9. Функция y = ax | 4 |
| 10. Понятие логарифма | 6 |
| 11. Свойства логарифмов | 6 |
| Зачет или контрольная работа № 3 | 1 |
| Глава 4. Тригонометрические функции | 42 |
| 12. Угол поворота | 1 |
| 13. Радианная мера угла | 2 |
| 14. Синус и косинус любого угла | 3 |
| 15. Тангенс и котангенс любого угла | 4 |
| 16. Простейшие тригонометрические уравнения | 4 |
| 17. Формулы приведения | 4 |
| 18. Свойства и график функции y = sin x | 4 |
| 19. Свойства и график функции y = cos x | 3 |
| 20. Свойства и график функции y = tg x и y = ctg x | 2 |
| Зачет или контрольная работа № 4 | 1 |
| 21. Зависимости между тригонометрическими функциями одного и того же аргумента | 3 |
| 22. Синус и косинус суммы и разности двух углов | 2 |
| 23. Тангенс суммы и тангенс разности двух углов | 2 |
| 24. Тригонометрические функции двойного угла | 2 |
| 25. Преобразование произведения тригонометрических функций в сумму. Обратное преобразование | 3 |
| 26. Решение тригонометрических уравнений | 4 |
| Зачет или контрольная работа № 5 | 1 |
| Глава 5. Вероятность и статистика | 5 |
| 27. Понятие вероятности | 2 |
| 28. Вычисление числа вариантов | 2 |
| Зачет или контрольная работа № 6 | 1 |
| Глава 6. Повторение (Итоговая контрольная работа) | 12 |
| ВСЕГО | 105 |
ТРЕБОВАНИЯ К РЕЗУЛЬТАТАМ ОСВОЕНИЯ УЧЕБНОГО ПРЕДМЕТА
Программа предполагает достижение выпускниками старшей школы следующих результатов:
— целостного мировоззрения, соответствующего современному уровню развития науки математики и общественной практики ее применения;
— основ саморазвития и самовоспитания в соответствии с общечеловеческими ценностями и идеалами гражданского общества; готовности и способности к самостоятельной, творческой и ответственной деятельности с применением методов математики;
— готовности и способности к образованию, в том числе самообразованию, на протяжении всей жизни; сознательного отношения к непрерывному образованию как условию успешной профессиональной и общественной деятельности на основе развитой мотивации учебной деятельности и личностного смысла изучения математики, заинтересованности в приобретении и расширении математических знаний и способов действий, осознанности в построении индивидуальной образовательной траектории;
— осознанного выбора будущей профессии, ориентированной на применение математических методов и возможностей реализации собственных жизненных планов; отношения к профессиональной деятельности как к возможности участия в решении личных, общественных, государственных, общенациональных проблем;
— логического мышления: критичности (умение распознавать логически некорректные высказывания), креативности (собственная аргументация, опровержения, постановка задач, формулировка проблем, работа над исследовательским проектом
и др.).
— способности самостоятельно ставить цели учебной и исследовательской, проектной деятельности, планировать, осуществлять, контролировать и оценивать учебные действия в соответствии с поставленной задачей и условиями ее выполнения;
— умения самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
— умения находить необходимую информацию, критически оценивать и интерпретировать информацию в различных источниках (в справочниках, литературе, Интернете), представлять информацию в различной форме (словесной, табличной, графической, символической), обрабатывать, хранить и передавать информацию в соответствии с познавательными или коммуникативными задачами;
— навыков осуществления познавательной, учебно-исследовательской и проектной деятельности, навыками разрешения проблем; способность и готовность к самостоятельному поиску методов решения практических задач, применению различных методов познания;
— умения продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности, эффективно разрешать конфликты;
— владения языковыми средствами — умения ясно, логично и точно излагать свою точку зрения, использовать адекватные языковые средства;
— владения навыками познавательной рефлексии как осознания совершаемых действий и мыслительных процессов, их результатов и оснований, границ своего знания и незнания, новых познавательных задач и средств их достижения.
— представлений о математике как части мировой культуры и о месте математики в современной цивилизации, о способах описания на математическом языке явлений реального мира;
— представлений о математических понятиях как о важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий;
— умений применения методов доказательств и алгоритмов решения; умения их применять, проводить доказательные рассуждения в ходе решения задач;
— стандартных приемов решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем; использования готовых компьютерных программ, в том числе для поиска пути решения и иллюстрации решения уравнений и неравенств;
— умений описывать круг математических задач, для решения которых требуется введение новых понятий (степень, арифметический корень, логарифм; синус, косинус, тангенс, котангенс; арксинус, арккосинус, арктангенс, арккотангенс; решать практические расчетные задачи из окружающего мира, включая задачи по социально-экономической тематике, а также из смежных дисциплин;
— умений приводить примеры реальных явлений (процессов), количественные характеристики которых описываются с помощью функций; использовать готовые компьютерные программы для иллюстрации зависимостей; описывать свойства функций с опорой на их графики; соотносить реальные зависимости из окружающей жизни и из смежных дисциплин с элементарными функциями, делать выводы о свойствах таких зависимостей;
— представлений о процессах и явлениях, имеющих вероятностный характер, о статистических закономерностях в реальном мире, об основных понятиях элементарной теории вероятностей; умений находить и оценивать вероятности наступления событий в простейших практических ситуациях и основные характеристики случайных величин;
— навыков использования готовых компьютерных программ при решении задач.
УЧЕБНО-МЕТОДИЧЕСКОЕ И МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ
ОБЕСПЕЧЕНИЕ ОБРАЗОВАТЕЛЬНОГО ПРОЦЕССА
Муравина О. В. Рабочая программа. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10—11 классы
Муравин Г. К., Муравина О. В. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. Базовый уровень.10 класс.
Башмаков М. И. Математика в кармане ≪Кенгуру≫. Международные олимпиады школьников.
Звавич Л. И., Рязановский А. Р. Алгебра в таблицах.7—11 классы. Справочное пособие.
Математика в формулах. 5—11 классы. Справочное пособие. Беляева Э. С., Потапов А. С., Титоренко С. А.
Уравнения и неравенства с параметром. Учебный комплект в 2 ч. c мультимедийным приложением. (Выпускной/Вступительный экзамен).
Богомолов Н. В. Математика. Задачи с решениями. Учебное пособие.
Черкасов О.Ю., Якушев А. Г. Математика. Учебное пособие.
Петров В. А. Математика. 5—11 классы. Прикладные Задачи
СD-ROM ≪Подготовка к ЕГЭ по математике≫. Электронное пособие.
СD-ROM ≪Алгебра. Графики функций≫.
Интерактивное наглядное пособие.
CD-ROM ≪История математики≫







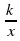 , их свойства и графики. График дробно-линейной функции. Степенная функция с натуральным показателем, функция y =
, их свойства и графики. График дробно-линейной функции. Степенная функция с натуральным показателем, функция y = 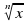 , их свойства и графики.
, их свойства и графики. 









