Составила учитель математики
Сляднева Екатерина Александровна
учебный год
ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ ИЗУЧЕНИЯ ПРЕДМЕТА
умение самостоятельно определять цели своего обучения, ставить и формулировать для себя новые задачи в учебе и познавательной деятельности, развивать мотивы и интересы своей познавательной деятельности;
умение самостоятельно планировать пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией;
умение оценивать правильность выполнения учебной задачи, собственные возможности ее решения;
владение основами самоконтроля, самооценки, принятия решений и осуществления осознанного выбора в учебной и познавательной деятельности;
умение определять понятия, создавать обобщения, устанавливать аналогии, классифицировать, устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение и делать выводы;
умение создавать, применять и преобразовывать знаки и символы, модели и схемы для решения учебных и познавательных задач;
смысловое чтение; умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками;
работать индивидуально и в группе; умение осознанно использовать речевые средства в соответствии с задачей коммуникации для выражения своих чувств, мыслей и потребностей;
планирования и регуляции своей деятельности; владение устной и письменной речью.
готовность и способность обучающихся к саморазвитию и личностному самоопределению,
сформированность их мотивации к обучению и целенаправленной познавательной деятельности, системы значимых социальных и межличностных отношений, ценностно-смысловых установок,
способность ставить цели и строить жизненные планы.
Формирование представлений о математике как о методе познания действительности, позволяющем описывать и изучать реальные процессы и явления.
Развитие умений работать с учебным математическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли с применением математической терминологии и символики, проводить классификации, логические обоснования, доказательства математических утверждений.
Овладение геометрическим языком; развитие умения использовать его для описания предметов окружающего мира;
развитие пространственных представлений, изобразительных умений, навыков геометрических построений.
Формирование систематических знаний о плоских фигурах и их свойствах;
развитие умений моделирования реальных ситуаций на языке геометрии, исследования построенной модели с использованием геометрических понятий и теорем, аппарата алгебры, решения геометрических и практических задач.
2. СОДЕРЖАНИЕ УЧЕБНОГО ПРЕДМЕТА
Математический язык. Математическая модель
Числовые и алгебраические выражения. Что такое математический язык и математическая модель. Линейное уравнение с одной переменной. Линейное уравнение с одной переменной как математическая модель реальной ситуации. Координатная прямая. Виды числовых промежутков на координатной прямой.
Сформировать умение составлять числовые и буквенные выражения, записывать математические свойства, правила, формулы на математическом языке; осуществлять числовые подстановки в алгебраические выражения и формулы и выполнять соответствующие вычисления; выражать из формулы одну переменную через другие; находить область допустимых значений переменных в выражении.
Сформировать умение распознавать и решать линейные уравнения и уравнения, сводящиеся к ним; решать текстовые задачи алгебраическим методом: описывать реальную ситуацию в виде математической модели – линейного уравнения, решать полученное уравнение и интерпретировать результат.
Сформировать умение изображать числа и числовые промежутки на координатной прямой, определять принадлежность точки данному числовому промежутку.
Линейная функция
Координатная плоскость. Линейное уравнение с двумя переменными. Линейная функция. Возрастание и убывание линейной функции. Взаимное расположение графиков линейных функций.
Определять координаты точек, данных на координатной плоскости.
Строить на координатной плоскости точки и фигуры по заданным координатам, фигуры, симметричные данным относительно координатных осей и начала координат.
Сформировать понятие линейного уравнения с двумя переменными, умение узнавать указанные уравнения, выражать в них одну переменную через другую, определять, является ли пара чисел решением уравнения с двумя переменными, строить прямую, которая является графиком данного линейного уравнения с двумя переменными. Приводить примеры решений уравнений с двумя переменными; решать задачи, алгебраической моделью которых является уравнение с двумя переменными; находить целочисленные решения (подбором).
Сформировать понятие линейной функции, независимой переменной – аргумента, зависимой переменной, умение составлять таблицы значений линейной функции. Сформировать умение строить и читать графики линейной функции, находить по графику значение одной переменной по значению другой, определять наименьшее и наибольшее значения линейной функции на заданном промежутке. Решать графически линейные уравнения и неравенства. Показывать схематически положение на координатной плоскости графиков функций 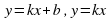 в зависимости от значений коэффициентов k и b.
в зависимости от значений коэффициентов k и b.
Системы двух линейных уравнений с двумя переменными
Основные понятия о системах двух линейных уравнений с двумя переменными. Методы решения систем двух линейных уравнений с двумя переменными: графический, подстановки и алгебраического сложения. Системы двух линейных уравнений как математические модели реальных ситуаций.
Сформировать понятие о системах двух линейных уравнений с двумя переменными, умение узнавать указанные системы, определять, является ли пара чисел решением системы двух линейных уравнений с двумя переменными.
Сформировать умение решать системы двух линейных уравнений с двумя переменными графическим методом, использовать функционально-графические представления для исследования систем уравнений на предмет числа решений. Решать системы двух линейных уравнений с двумя переменными методами подстановки и алгебраического сложения.
Сформировать умение решать текстовые задачи алгебраическим методом, составляя математическую модель задачи в виде системы двух линейных уравнений с двумя переменными, решать полученную систему и интерпретировать результат.
Степень с натуральным показателем и ее свойства
Понятие степени с натуральным показателем; свойства степеней. Степень с нулевым показателем.
Сформировать понятие степени с натуральным и нулевым показателем и знание свойств степени, умение вычислять степень числа, знание табличных значений степеней 2, 3, 5, 10. Применять свойства степени для преобразования выражений и вычислений.
Сформировать умение конструировать математические предложения с помощью связок «если…, то…», воспроизводить несложные доказательства изученных теорем о свойствах степени с натуральным показателем. Решать простые уравнения, используя определение степени с неотрицательным целым показателем.
Одночлены. Арифметические операции над одночленами
Понятие одночлена. Стандартный вид одночлена. Сложение и вычитание одночленов. Умножение одночленов. Возведение одночленов в натуральную степень. Деление одночлена на одночлен.
Сформировать понятия одночлена, стандартного вида одночлена, подобных одночленов. Уметь приводить одночлены к стандартному виду, выполнять сложение и вычитание подобных одночленов, умножение одночленов, возведение одночлена в степень, деление одночлена на одночлен (в корректных случаях).
Многочлены. Арифметические операции над многочленами
Понятие многочлена. Сложение и вычитание многочленов. Умножение многочлена на одночлен. Умножение многочлена на многочлен. Формулы сокращенного умножения. Деление многочлена на одночлен.
Сформировать понятие многочлена, записи многочлена в стандартном виде. Выполнять сложение и вычитание многочленов, умножение многочлена на одночлен, умножение многочлена на многочлен. Применять правило умножения многочленов для выведения формул разности квадратов, квадрата двучлена и суммы (разности) кубов. Применять формулы сокращенного умножения для преобразования алгебраических выражений. Сформировать умение выполнять деление многочлена на одночлен (в корректных случаях).
Применять различные формы самоконтроля при выполнении преобразований.
Разложение многочленов на множители
Понятие о разложении многочлена на множители. Вынесение общего множителя за скобки. Способ группировки. Разложение многочлена на множители с помощью формул сокращенного умножения и комбинации различных приемов. Сокращение алгебраических дробей. Тождества.
Сформировать умение видеть способ, которым данный многочлен можно разложить на множители и выполнять это разложение. Применять формулы сокращенного умножения для разложения многочлена на множители, для решения уравнений, сокращения алгебраических дробей, доказательства делимости значения числового выражения на число, а также как способ рационализации вычислений. Сформировать понятие тождества и тождественного преобразования выражений.
Функция 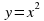
Функция 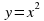 и ее график. Функция
и ее график. Функция 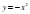 и ее график. Графическое решение уравнений. Функциональная символика.
и ее график. Графическое решение уравнений. Функциональная символика.
Познакомить учащихся с первыми нелинейными функциями – функциями 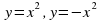 . Вычислять значения этих функций, составлять таблицы значений функции, строить графики функций и описывать их свойства на основе графических представлений. Сформировать умение графически решать уравнения, системы уравнений и простейшие неравенства. Сформировать первоначальное умение строить график кусочной функции и проводить на основе графических представлений простейшие исследования. Сформировать понятие о функциональной символике, умение находить значение функции, используя функционально-символическую запись, осуществлять подстановку одного выражения в другое. Использовать функциональную символику для записи разнообразных фактов, связанных с рассматриваемыми функциями. Строить речевые конструкции с использованием функциональной терминологии.
. Вычислять значения этих функций, составлять таблицы значений функции, строить графики функций и описывать их свойства на основе графических представлений. Сформировать умение графически решать уравнения, системы уравнений и простейшие неравенства. Сформировать первоначальное умение строить график кусочной функции и проводить на основе графических представлений простейшие исследования. Сформировать понятие о функциональной символике, умение находить значение функции, используя функционально-символическую запись, осуществлять подстановку одного выражения в другое. Использовать функциональную символику для записи разнообразных фактов, связанных с рассматриваемыми функциями. Строить речевые конструкции с использованием функциональной терминологии.
Итоговое повторение
3. ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ С ОПРЕДЕЛЕНИЕМ ОСНОВНЫХ ВИДОВ УЧЕБНОЙ ДЕЯТЕЛЬНОСТИ
| Раздел учебного курса, кол-во часов | Кол-во часов | Элементы содержания | Виды деятельности учащихся |
| Глава 1. Математический язык. Математическая модель.
| 13 ч | 1. Числовые и алгебраические выражения. 2. Что такое математический язык. 3. Что такое математическая модель. 4. Линейное уравнение с одной переменной. 5. Координатная прямая | Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль. Вычисление значений числовых выражений, применение свойств и правил арифметических действий, выбор рациональных способов вычислений. Чтение выражений, формул, правил, записанных на математическом языке, перевод словесных формулировок на математический язык. Использование символики для записи математических утверждений. Работа в паре и группе. Участие в деловой игре. Описание реальных ситуаций с помощью математических моделей. Планирование хода решения задач с использованием трех этапов математического моделирования. Прогнозирование результата решения, оценка реальности полученного ответа. Применение алгоритма при решении линейного уравнения. Изображение чисел и числовых промежутков на числовой прямой. Чтение учебника, извлечение информации в соответствии с темой урока и заданием учителя. Выполнение упражнений по правилу, образцу и алгоритму. Подведение итогов. Самооценка знаний. |
| Глава 2. Линейная функция
| 12 ч | 1. Координатная плоскость 2. Линейное уравнение с двумя переменными 3. Линейная функция 4. Линейная функция 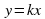 5. Взаимное расположение графиков линейных функций | Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль. Построение точек и геометрических фигур в координатной плоскости. Построение прямой, заданной линейным уравнением с двумя переменными. Моделирование реальной ситуации с помощью линейного уравнения с двумя переменными. Исследование графической модели с точки зрения реальности результата. Проведение аналогии между линейным уравнением с двумя переменными и линейной функцией. Работа в паре и в группе. Построение графика линейной функции, в том числе на заданном промежутке. Чтение графика, нахождение наибольшего и наименьшего значений функции. Анализ поведения графика линейной функции в зависимости от значений коэффициентов k и m на основе наблюдения и сравнения. Работа в группе. Исследование взаимного расположения графиков линейных функций. Работа в группе. Самостоятельное изучение материала учебника, извлечение учебной информации, осмысление ее и применение в учебной деятельности. Выполнение упражнений по аналогии, алгоритму, образцу. Самоконтроль решения. Участие в мини проектной деятельности «Линейная функция как модель описания реальных ситуаций». Поиск, обнаружение и устранение ошибок при построении графиков линейного уравнения с двумя переменными и линейной функции. Подведение итогов: что нового узнали, чему научились. Самооценка знаний. |
| Глава 3. Системы двух линейных уравнений с двумя переменными | 13 ч | 1. Основные понятия 2. Метод подстановки 3. Метод алгебраического сложения 4. Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций | Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль. Изучение новой математической модели – системы двух линейных уравнений с двумя переменными. Проведение аналогии между взаимным расположением двух прямых на координатной плоскости и графическим методом решения систем двух линейных уравнений с двумя переменными. Составление алгоритма решения систем графическим методом. Исследование систем уравнений на предмет числа решений с помощью функционально-графических представлений. Поиск решения в проблемной ситуации в случаях неточности и недостаточности применения графического метода решения систем (точка пересечения неточна или слишком удалена). Работа в группе. Составление алгоритма решения систем методом постановки и алгебраического сложения. Работа в паре. Выполнение самоконтроля при решении систем. Поиск, обнаружение и устранение ошибок при решении систем. Описание реальных ситуаций с помощью систем двух линейных уравнений с двумя переменными. Решение задач в три этапа математического моделирования. Участие в мини проектной деятельности «Моделирование реальных ситуаций с помощью систем линейных уравнений». Отыскание информации на заданную тему в учебнике. Подведение итогов: что нового узнали, чему научились. Самооценка знаний. |
| Глава 4. Степень с натуральным показателем и её свойства | 6 ч | 1. Что такое степень с натуральным показателем 2. Таблица основных степеней 3. Свойства степени с натуральным показателем 4. Умножение и деление степеней с одинаковым показателем 5. Степень с нулевым показателем | Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль. Чтение и запись степени выражения, свойств степени на математическом языке. Составление таблицы степеней. Изучение по учебнику этапов теоретического исследования. Самостоятельное проведение исследования. Доказательство свойств степени. Конструирование предложений с помощью связок «если…, то…». Работа в паре. Применение определения и свойств степени при решении простейших уравнений, моделирование реальных ситуаций, приводящих к простейшему степенному уравнению. Мини проект. Осуществление самоконтроля решения, поиск и устранение ошибок. Подведение итогов: что нового узнали, чему научились. Самооценка знаний. |
| Глава 5. Одночлены. Арифметические операции над одночленами | 9 ч | 1. Понятие одночлена. 2. Стандартный вид одночлена 3. Сложение и вычитание одночленов 4. Умножение одночленов. Возведение одночлена в степень 5. Деление одночлена на одночлен
| Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль. Самостоятельное чтение учебника с целью поиска информации на заданную тему. Выполнение алгебраических преобразований с одночленами, пошаговый контроль правильности выполнения алгоритма преобразования. Работа в паре. Сравнение двух дробей по виду и выявление, которая из них является одночленом, а которая нет, обоснование вывода. Составление алгоритма приведения одночлена к стандартному виду, сложения одночленов. Работа в паре. Выполнение действий с одночленами. Описание реальных ситуаций с помощью модели (уравнения) с подобными одночленами. Решение задач в три этапа математического моделирования. Мини проект. Наблюдение и вывод, в каком случае один одночлен можно разделить на другой одночлен и как это сделать. Выполнение заданий, связанных с выявлением некорректных высказываний. Самоконтроль выполнения действий и преобразований с одночленами, поиск и устранение ошибок. Подведение итогов: что нового узнали, чему научились. Самооценка знаний. |
| Глава 6. Мнгогочлены. Арифметические операции над многочленами | 16 ч | 1. Основные понятия 2. Сложение и вычитание многочленов 3. Умножение многочлена на одночлен 4. Умножение многочлена на многочлен 5. Формулы сокращенного умножения 6. Деление многочлена на одночлен | Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль. Извлечение информации из учебника, связанной с изучением нового материала. Выполнение действий с многочленами по правилам. Работа в паре. Описание реальных ситуаций с помощью математической модели, представляющей собой многочлены. Решение задач в три этапа математического моделирования. Мини проект. Вывод формул сокращенного умножения. Чтение их и запись на математическом языке. Применение геометрической модели, иллюстрирующей вывод формул разности квадратов и квадрата суммы и разности. Выполнение преобразований многочленов, пошаговый контроль правильности и полноты выполнения алгоритма. Поиск, обнаружение и устранение арифметических и алгебраических ошибок. Подведение итогов: что нового узнали, чему научились. Самооценка знаний. |
| Глава 7. Разложение многочленов на множители | 18 ч | 1. Что такое разложение многочлена на множители и зачем оно нужно 2. Вынесение общего множителя за скобки 3. Способ группировки 4. Разложение многочлена на множители с помощью формул сокращенного умножения 5. Разложение многочлена на множители с помощью комбинации различных приемов 6. Сокращение алгебраических дробей 7. Тождества | Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль. Извлечение информации из учебника по заданной теме. Выделение существенного, главного. Чтение и запись на математическом языке при выполнении разложения на множители. Комментирование решений, разобранных в учебнике. Работа в паре. Выполнение преобразования в виде разложения многочлена на множители по алгоритму и образцу. Решение уравнений, построение графиков уравнений, выполнение арифметических действий, связанных с разложением на множители, сокращение дробей. Пошаговый самоконтроль за выполнением указанных действий. Поиск и устранение ошибок. Подведение итогов. Самооценка знаний. |
| Глава 8. Функция 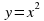 | 10 ч | 1. Функция 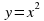 2. Графическое решение уравнений 3. Что означает в математике запись 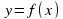
| Постановка цели и задач на каждом уроке. Планирование учебной деятельности на уроке и дома. Подведение итога на уроке: что нового узнали, чему научились. Самоконтроль. Чтение учебника и извлечение информации по заданной теме. Изучение новых функций 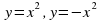 , графических моделей этих функций, свойств. , графических моделей этих функций, свойств. Построение и чтение графиков, в том числе кусочных функций. Проведение простейших исследований. Участие в проектной деятельности «Описание реальных ситуаций с помощью кусочных функций». Применение графических моделей для решения уравнений, неравенств, систем неравенств. Проверка найденных корней. Исследование взаимного расположения графика кусочной функции и прямой y = a на предмет числа общих точек при различных значениях а. Подведение итогов. Самооценка знаний. |
| Итоговое повторение | 8 ч |
| Постановка цели и задач на при повторении материала. Планирование учебной деятельности на уроке и дома. Подведение итога, коррекция знаний. Самоконтроль. |
| ИТОГО: | -
|
Приложение №1 Календарно-тематическое планирование
| № п/п | Содержание учебного материала | Цель урока | Планируемый результат обучения | Дата проведения |
| План | Факт |
| Глава 1 Математический язык. Математическая модель. 13ч |
| 1 | Числовые выражения. | Формирование новых знаний и умений | Знать: буквенные выражения (выражения с переменными). Числовое значение буквенного выражения. Допустимые значения переменных, входящих в алгебраическое выражение. Подстановка выражений вместо переменных. Равенство буквенных выражений. Тождество. Доказательство тождеств. Преобразование выражений. Уметь:Составлять буквенные выражения и формулы по условиям задач, осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные. |
|
|
| 2 | Значение числового выражения. | Формирование новых знаний и умений |
|
|
| 3 | Алгебраические выражения Допустимые значения переменных. | Формирование и совершенствование новых знаний |
|
|
| 4 | Что такое математический язык. | Формирование новых знаний и умений |
|
|
| 5 | Что такое математический модель? | Формирование новых знаний и умений |
|
|
| 6 | Составление математической модели | Формирование и совершенствование новых знаний |
|
|
| 7 | Составление математической модели. Закрепление знаний | закрепление и совершенствование новых знаний |
|
|
| 8 | Линейное уравнение с одной переменной | Формирование новых знаний и умений |
|
|
| 9 | Закрепление знаний по теме: линейное уравнение с одной переменной | Формирование и совершенствование новых знаний |
|
|
| 10 | Координатная прямая | Формирование новых знаний и умений |
|
|
| 11 | Закрепление знаний по теме: Координатная прямая | Формирование и совершенствование новых знаний |
|
|
| 12 | Контрольная работа №1 по теме Математический язык. Математическая модель |
| 13 | Анализ контрольной работы №1 | Работа над ошибками |
|
| Глава 2. Линейная функция. 12 ч |
| 14 | Координатная плоскость | Формирование новых знаний и умений | Знать: линейная функция, ее график, геометрический смысл коэффициентов. Функции описывающие прямую зависимость, их графики. Алгоритм нахождения координат точки на плоскости и отыскания точки по ее координатам. Алгоритм построения графика уравнения ах+ву+с=0. Уметь: решать линейные уравнения. Решать задачи с помощью уравнений с двумя переменными. Строить и читать график функции у=kx+b, y=kx. Определять взаимное расположение графиков линейных функций |
|
|
| 15 | Закрепление знаний по теме: Координатная плоскость | Применение знаний на практике |
|
|
| 16 | Линейное уравнение с двумя переменными и его график. | Формирование новых знаний и умений |
|
|
| 17 | Линейное уравнение с двумя переменными и его график. | Формирование и совершенствование новых знаний |
|
|
| 18 | Линейное уравнение с двумя переменными и его график. | Формирование новых знаний и умений |
|
|
| 19 | Линейная функция | Формирование новых знаний и умений |
|
|
| 20 | Линейная функция и её график | Применение знаний на практике |
|
|
| 21 | Закрепление знаний по теме: Линейная функция и её график | Совершенствование знаний, умений и навыков |
|
|
| 22 | Линейная функция у = кх | Формирование и совершенствование новых знаний |
|
|
| 23 | Взаимное расположение графиков линейных функций | Совершенствование знаний, умений и навыков |
|
|
| 24 | Контрольная работа №2 по теме Линейная функция |
|
| 25 | Анализ контрольной работы №2 | Работа над ошибками |
|
| Глава 3 Системы двух линейных уравнений с двумя переменными 13ч |
| 26 | Основные понятия | Формирование новых знаний и умений | Знать: графический метод решения систем уравнений. Метод подстановки и алгебраического сложения. Уметь: решать системы двух линейных уравнений методом подстановки, алгебраического сложения. Применять системы линейных уравнений при решении задач. Решать текстовые задачи алгебраическим методом, интерпретировать полученные результаты, проводить отбор решений, исходя из формулировки задачи. Находить значения аргумента по значению функции, заданной графиком или таблицей. Определять свойства функции по ее графику |
|
|
| 27 | Основные понятия |
|
|
|
| 28 | Метод подстановки | Формирование новых знаний и умений |
|
|
| 29 | Закрепление знаний по теме: Метод подстановки | Формирование и совершенствование новых знаний |
|
|
| 30 | Практикум по теме: Метод подстановки |
|
|
|
| 31 | Метод алгебраического сложения | Формирование новых знаний и умений |
|
|
| 32 | Метод алгебраического сложения | Совершенствование знаний, умений и навыков |
|
|
| 33 | Практикум по теме: Метод алгебраического сложения | Применение знаний на практике |
|
|
| 34 | Системы двух лин. уравнений с двумя переменными как мат модели реальных ситуаций | Формирование новых знаний и умений |
|
|
| 35 | Закрепление знаний по теме: Системы двух лин. уравнений с двумя переменными как мат модели реальных ситуаций | Применение знаний на практике |
|
|
| 36 | Практикум по теме: Системы двух лин. уравнений с двумя переменными как мат модели реальных ситуаций, подготовка к к/р | Применение знаний на практике |
|
|
| 37 | Контрольная работа №3 по теме Системы двух линейных уравнений с двумя переменными |
| 38 | Анализ контрольной работы №3 | Работа над ошибками |
|
| Глава 4 Степень с натуральным показателем 6ч |
| 39 | Что такое степень с натуральным показателем | Формирование и совершенствование новых знаний | Знать: понятие степени с натуральным показателем. Компоненты степени. Свойства степеней с целым показателем. Уметь: читать степени любых чисел с любым натуральным показателем и выполнять операцию возведения в степень. Составлять таблицы основных степеней и пользоваться ими при вычислении и нахождении значений выражений. Выполнять основные действия со степенями |
|
|
| 40 | Таблица основных степеней | Формирование и совершенствование новых знаний |
|
|
| 41 | Свойства степени с нат показателем | Формирование новых знаний и умений |
|
|
| 42 | Закрепление знаний по теме: Свойства степени с нат показателем | Применение знаний на практике |
|
|
| 43 | Умножение и деление степеней с одинаковыми показателями | Совершенствование знаний, умений и навыков |
|
|
| 44 | Степень с нулевым показателем | Формирование новых знаний и умений |
|
|
| Глава 5 Одночлены. Операции над одночленами 9ч |
| 45 | Понятие одночлена. Стандартный вид одночлена | Формирование новых знаний и умений | Знать: понятие одночлена. Правила сложения, вычитания, умножения и деления одночленов. Стандартный вид одночлена. Коэффициент и буквенная часть. Уметь: приводить примеры и определять является ли выражение одночленом, а также указывать его коэффициент и буквенную часть. Приводить одночлены к стандартному виду. Выполнять основные действия с одночленами. |
|
|
| 46 | Сложение и вычитание одночленов | Формирование новых знаний и умений |
|
|
| 47 | Закрепление знаний по теме: Сложение и вычитание одночленов | Применение знаний на практике |
|
|
| 48 | Умножение одночленов. Возведение в натуральную степень | Формирование новых знаний и умений |
|
|
| 49 | Закрепление знаний по теме Умножение одночленов. Возведение в натуральную степень | Применение знаний на практике |
|
|
| 50 | Деление одночлена на одночлен | Формирование новых знаний и умений |
|
|
| 51 | Закрепление знаний по теме Деление одночлена на одночлен | Совершенствование знаний, умений и навыков |
|
|
| 52 | Контрольная работа №4 по теме Одночлены. Операции над одночленами |
| 53 | Анализ контрольной работы №4 | Работа над ошибками |
|
| Глава 6 Многочлены. Арифметические действия над многочленами 16ч |
| 54 | Основные понятия | Формирование новых знаний и умений | Знать: понятие многочлена. Правила сложения, вычитания, умножения и деления многочленов. Формулы сокращенного умножения. Стандартный вид многочлена. Степень многочлена. Уметь: приводить примеры многочленов и определять, является ли выражение многочленом. Определять степень многочлена. Выполнять основные действия над многочленами. Выносить за скобки множитель. Уметь применять формулы сокращенного умножения |
|
|
| 55 | Сложение и вычитание многочленов | Формирование новых знаний и умений |
|
|
| 56 | Закрепление знаний по теме Сложение и вычитание многочленов | Формирование и совершенствование новых знаний |
|
|
| 57 | Умножение многочлена на одночлен | Формирование новых знаний и умений |
|
|
| 58 | Закрепление знаний по теме Умножение многочлена на одночлен | Применение знаний на практике |
|
|
| 59 | Умножение многочлена на многочлен | Формирование новых знаний и умений |
|
|
| 60 | Закрепление знаний по теме Умножение многочлена на многочлен | закрепление и совершенствование знаний |
|
|
| 61 | Практикум по теме: Умножение многочлена на многочлен | Применение знаний на практике |
|
|
| 62 | Формулы сокращённого умножения | Формирование новых знаний и умений |
|
|
| 63 | Формула квадрата суммы и разности | Формирование новых знаний и умений |
|
|
| 64 | формула разности квадратов | закрепление и совершенствование знаний |
|
|
| 65 | формулы суммы и разности кубов | Применение знаний на практике |
|
|
| 66 | Деление многочлена на одночлен | Применение знаний на практике |
|
|
| 67 | Повторительно – обобщающий урок Подготовка к к/р | Совершенствование знаний, умений и навыков |
|
|
| 68 | Контрольная работа№5 по теме: Многочлены. Арифметические действия над многочленами |
| 69 | Анализ контрольной работы №5 | Работа над ошибками |
| Глава 7 Разложение многочленов на множители 18ч |
|
| 70 | Что такое разложение и зачем оно нужно | Формирование новых знаний и умений | Знать: понятие многочлена. Правила сложения, вычитания, умножения и деления многочленов. Формулы сокращенного умножения. Стандартный вид многочлена. Степень многочлена. Уметь: приводить примеры многочленов и определять, является ли выражение многочленом. Определять степень многочлена. Выполнять основные действия над многочленами. Выносить за скобки множитель. Уметь применять формулы сокращенного умножения |
|
|
| 71 | Вынесение общего множителя за скобки | Формирование новых знаний и умений |
|
|
| 72 | Закрепление знаний по теме Вынесение общего множителя за скобки | Совершенствование знаний, умений и навыков |
|
|
| 73 | Способ группировки | Формирование новых знаний и умений |
|
|
| 74 | Способ группировки | Совершенствование знаний, умений и навыков |
|
|
| 75 | Разложение на множители с помощью ФСУ | Формирование новых знаний и умений |
|
|
| 76 | Закрепление знаний по теме Разложение на множители с помощью ФСУ | Формирование и совершенствование новых знаний |
|
|
| 77 | Закрепление знаний по теме Разложение на множители с помощью ФСУ | Применение знаний на практике |
|
|
| 78 | Практикум по теме: Разложение на множители с помощью ФСУ | Применение знаний на практике |
|
|
| 79 | Практикум. Самостоятельная работа | Совершенствование знаний, умений и навыков |
|
|
| 80 | Разложение с помощью комбинации различных методов | Формирование новых знаний и умений |
|
|
| 81 | Закрепление знаний по теме: Разложение с помощью комбинации различных методов | Совершенствование знаний, умений и навыков |
|
|
| 82 | практикум по теме: Разложение с помощью комбинации различных методов | Совершенствование знаний, умений и навыков |
|
|
| 83 | Сокращение алгебраических дробей | Формирование новых знаний и умений |
|
|
| 84 | Закрепление знаний по теме Сокращение алгебраических дробей | Применение знаний на практике |
|
|
| 85 | Тождества | Формирование новых знаний и умений |
|
|
| 86 | Контрольная работа №6 по теме: Разложение многочленов на множители |
| 87 | Анализ контрольной работы №6 | Работа над ошибками |
| Глава 8 Функция у=х2 10ч |
| 88 | Функция у=х2 и её график | Формирование новых знаний и умений | Знать: квадратичная функция, ее график, парабола. Область определения функции, непрерывность функции. Уметь: строить и читать график функции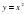 . Применять основные алгоритмические приемы графического решения уравнений. Находить значения функции, заданной формулой, таблицей, графиком по ее аргументу, находить значение аргумента по значению функции, заданной графиком или таблицей. Определять свойства функции по ее графику, применять графические представления при решении уравнений . Применять основные алгоритмические приемы графического решения уравнений. Находить значения функции, заданной формулой, таблицей, графиком по ее аргументу, находить значение аргумента по значению функции, заданной графиком или таблицей. Определять свойства функции по ее графику, применять графические представления при решении уравнений |
|
|
| 89 | Закрепление знаний по теме Функция у=х2 и её график | Применение знаний на практике |
|
|
| 90 | Практикум по теме: Функция у=х2 и её график | Совершенствование знаний, умений и навыков |
|
|
| 91 | Графическое решение уравнений | Формирование новых знаний и умений |
|
|
| 92 | Практикум по теме Графическое решение уравнений | Применение знаний на практике |
|
|
| 93 | Что означает в математике запись у =f(х) |
|
|
|
| 94 | Закрепление знаний по теме Что означает в математике запись у =f(х) | Совершенствование знаний, умений и навыков |
|
|
| 95 | Практикум по теме Что означает в математике запись у =f(х) |
|
|
|
|
| 96 | Контрольная работа №7 по теме: Функция у=х2 |
| 97 | Анализ контрольной работы №7 | Работа над ошибками |
|
| Итоговое повторение 8ч |
| 98 | Функции и графики | Совершенствование знаний, умений и навыков Применение знаний на практике |
|
|
|
| 99 | Линейная функция |
|
|
| 100 | Системы двух линейных уравнений с двумя переменными. |
|
|
| 101 | Системы двух линейных уравнений с двумя переменными. |
|
|
| 102 | Системы двух линейных уравнений с двумя переменными |
|
|
| 103 | Степень с натуральным показателем и её свойства
|
|
|
| 104 | Одночлены. Арифметические операции над одночленами
|
|
|
|
|
| 105 | Многочлены. Арифметические операции над многочленами. |
|
|
|
|
|
|
|
СИСТЕМА ОЦЕНИВАНИЯ В ПРЕДМЕТЕ
Критерии оценивания знаний, умений и навыков обучающихся по математике.
Для оценки достижений учащихся применяется пятибалльная система оценивания.
Нормы оценки:
1. Оценка письменных контрольных работ обучающихся по математике.
Ответ оценивается отметкой «5», если:
1) работа выполнена полностью;
2) в логических рассуждениях и обосновании решения нет пробелов и ошибок;
3) в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится, если:
1) работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
2)допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
1) допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
1) допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2.Оценка устных ответов обучающихся по математике
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке учащихся» в настоящей программе по математике);
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Итоговая оценка знаний, умений и навыков
1. За учебную четверть и за год знания, умения и навыки учащихся по математике оцениваются одним баллом.
2. Основанием для выставления итоговой оценки знаний служат результаты наблюдений учителя за повседневной работой учеников, устного опроса, текущих и итоговых контрольных работ. Однако последним придается наибольшее значение.
При выставлении итоговой оценки учитывается как уровень теоретических знаний ученика, так и овладение им практическими умениями и навыками. Однако ученику не может быть выставлена положительная итоговая оценка по математике, если все или большинство его текущих обучающих и контрольных работ, а также итоговая контрольная работа оценены как неудовлетворительные, хотя его устные ответы оценивались положительно.
10






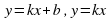 в зависимости от значений коэффициентов k и b.
в зависимости от значений коэффициентов k и b.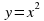
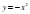 и ее график. Графическое решение уравнений. Функциональная символика.
и ее график. Графическое решение уравнений. Функциональная символика.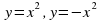 . Вычислять значения этих функций, составлять таблицы значений функции, строить графики функций и описывать их свойства на основе графических представлений. Сформировать умение графически решать уравнения, системы уравнений и простейшие неравенства. Сформировать первоначальное умение строить график кусочной функции и проводить на основе графических представлений простейшие исследования. Сформировать понятие о функциональной символике, умение находить значение функции, используя функционально-символическую запись, осуществлять подстановку одного выражения в другое. Использовать функциональную символику для записи разнообразных фактов, связанных с рассматриваемыми функциями. Строить речевые конструкции с использованием функциональной терминологии.
. Вычислять значения этих функций, составлять таблицы значений функции, строить графики функций и описывать их свойства на основе графических представлений. Сформировать умение графически решать уравнения, системы уравнений и простейшие неравенства. Сформировать первоначальное умение строить график кусочной функции и проводить на основе графических представлений простейшие исследования. Сформировать понятие о функциональной символике, умение находить значение функции, используя функционально-символическую запись, осуществлять подстановку одного выражения в другое. Использовать функциональную символику для записи разнообразных фактов, связанных с рассматриваемыми функциями. Строить речевые конструкции с использованием функциональной терминологии.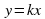
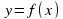
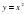 . Применять основные алгоритмические приемы графического решения уравнений. Находить значения функции, заданной формулой, таблицей, графиком по ее аргументу, находить значение аргумента по значению функции, заданной графиком или таблицей. Определять свойства функции по ее графику, применять графические представления при решении уравнений
. Применять основные алгоритмические приемы графического решения уравнений. Находить значения функции, заданной формулой, таблицей, графиком по ее аргументу, находить значение аргумента по значению функции, заданной графиком или таблицей. Определять свойства функции по ее графику, применять графические представления при решении уравнений









