ЧОУ СОШ «Оренбургская Епархиальная православная гимназия им. св. пр. Иоанна Кронштадтского»
| Рассмотрено на заседании ШМО Руководитель МО ___________ // подпись ФИО Протокол №__6__ от «15» июня 2016г.
| Согласовано Заместитель руководителя по УВР _____________/Н.Н. Каневская/ подпись ФИО «26» августа 2016г.
| Утверждено Ректор гимназии ___________ /протоиерей Георгий Горлов / подпись ФИО Протокол №_1_ от « 30 » августа 2016г.
|
РАБОЧАЯ ПРОГРАММАЭЛЕКТИВНОГО КУРСА
для 11 класса
«Подготовка к ЕГЭ»
Автор-составитель: Болдырева Татьяна Александровна, учитель математики, 1 квалификационной категории
2016 г.
Оренбург
Оглавление
Раздел I. Планируемые результаты освоения учебного предмета, курса 3
Раздел II. Содержание учебного предмета, курса 4
Раздел III. Тематическое планирование с указанием количества часов, отводимых на освоение каждой темы 5
Приложение
Календарно-тематическое планирование 8
Учебно-методическое и материально-техническое обеспечение 11
Оценочные материалы 12
Рабочая программа элективного курса предназначена для 11класса разработанана основании следующих документов:
Федеральный закон "Об образовании в Российской Федерации"от 29.12.2012 N 273-ФЗ;
Федеральный государственный образовательный компонент );
ООП ООО ЧОУ СОШ «Оренбургская Епархиальная православная гимназия им. св. пр. Иоанна Кронштадтского» (протокол № 1 от 30.08.2016 );
положение о рабочей программе ЧОУ СОШ «Оренбургская Епархиальная православная гимназия имени св. пр. Иоанна Кронштадтского» (протокол № 6 от 31.05.2016 г )
Планируемые результаты освоения учебного предмета, курса
Изучение данного курса дает обучающимся возможность:
Повторить и систематизировать ранее изученный материал школьного курса математики;
Освоить основные приемы решения задач;
Овладеть навыками построения и анализа предполагаемого решения поставленной задачи;
Познакомиться и использовать на практике нестандартные методы решения задач;
Повысить уровень своей математической культуры, творческого развития, познавательной активности;
Познакомиться с возможностями использования электронных средств обучения, в том числе интернет-ресурсов, в ходе подготовки к итоговой аттестации в форме ЕГЭ.
Содержание учебного предмета, курса
Модуль тригонометрия
Простейшие тригонометрические уравнения. Прикладные задачи, сводящиеся к решению простейших тригонометрических уравнений и неравенств.
Решение тригонометрических уравнений с последующим отбором корней.
Модуль производная и ее применение
Физический и геометрический смысл производной. Производная и исследование функций. Возрастание и убывание функции. Экстремумы. Чтение графиков функции и графиков производной функции. Наибольшее и наименьшее значение функции.
Модуль комбинаторика и теория вероятности
Комбинаторика. Поочередный и одновременный выбор. Размещения с повторениями, сочетания с повторениями. Перестановки.
Вероятность. Частота события, вероятность. Равновозможные события и подсчет их вероятности. Геометрическая вероятность. Вероятности событий. Условная вероятность. Независимость событий. Вероятность произведения независимых событий. Формула Бернулли. Решение задач.
Статистические данные. Представление данных в виде таблиц, диаграмм, графиков. Понятие о статистическом выводе на основе выборки.
Тематическое планирование с указанием количества часов, отводимых на освоение каждой темы.
| № п/п | Наименование разделов | Наименование тем | Количество часов | В том числе, количество часов на проведение |
| Лабораторных работ | Практических работ | Контрольных работ |
| 1 | Алгебра | Простейшие тригонометрические уравнения. | 11 |
|
| 2 |
|
| Прикладные задачи, сводящиеся к решению простейших тригонометрических уравнений и неравенств. |
|
|
|
|
|
| Решение тригонометрических уравнений с последующим отбором корней. |
|
|
|
|
| 2 | Начала математического анализа | Производная и ее применение
| 11 |
|
| 2 |
|
|
| Физический и геометрический смысл производной |
|
|
|
|
|
| Производная и исследование функций. Возрастание и убывание функции. Экстремумы. |
|
|
|
|
|
| Чтение графиков функции и графиков производной функции. |
|
|
|
|
|
| Наибольшее и наименьшее значение функции. |
|
|
|
|
| 3 | Элементы комбинаторики, статистики и теории вероятностей | Комбинаторика. Поочередный и одновременный выбор. Размещения с повторениями, сочетания с повторениями. Перестановки. | 11 |
|
| 1 |
| Вероятность. Частота события, вероятность. Равновозможные события и подсчет их вероятности. |
|
|
| Геометрическая вероятность. Вероятности событий. Условная вероятность. |
|
|
| Независимость событий. Вероятность произведения независимых событий. Формула Бернулли. |
|
|
| Статистические данные. Представление данных в виде таблиц, диаграмм, графиков. Понятие о статистическом выводе на основе выборки. |
|
|
| 4 | Итоговое занятие |
| 1 |
|
|
|
|
| Итого |
| 34 |
|
| 5 |
Наименование и количество контрольных мероприятий в рамках тематического и итогового контроля
| № | Наименование раздела | Наименование работы | Дата |
| 1 | Алгебра | Контрольная работа №1 «Решение простейших тригонометрических уравнений».
Контрольная работа №2 «Решение тригонометрических уравнений с последующим отбором корней». |
|
|
2
| Начала математического анализа | Контрольная работа № 3 по теме «Производная. Ее физический и геометрический смысл.Возрастание и убывание функции. Экстремумы. ».
Контрольная работа № 4 по теме «Чтение графиков функции и графиков производной функции. Наибольшее и наименьшее значение функции». |
|
|
3
| Элементы комбинаторики, статистики и теории вероятностей | Контрольная работа № 5 «Элементы комбинаторики, статистики и теории вероятностей». |
|
Приложение
(календарно-тематическое планирование, оценочные материалы)
Календарно-тематическое планирование
| № урока | Наименование тем | Содержание образования в соответствии с ФК ГОС | Кол-во. часов | Дата | Корректировка |
| 1 | Простейшие тригонометрические уравнения | Решать тригонометрические уравнения | 1 | 6.09 |
|
| 2 | Простейшие тригонометрические уравнения | Решать тригонометрические уравнения | 1 | 13.09 |
|
| 3 | Простейшие тригонометрические уравнения | Решать тригонометрические уравнения | 1 | 20.09 |
|
| 4 | Контрольная работа №1 «Решение простейших тригонометрических уравнений». |
| 1 | 27.09 |
|
| 5 | Прикладные задачи, сводящиеся к решению простейших тригонометрических уравнений и неравенств. | Решать тригонометрические уравнения | 1 | 4.10 |
|
| 6 | Прикладные задачи, сводящиеся к решению простейших тригонометрических уравнений и неравенств. | Решать тригонометрические уравнения | 1 | 11.10 |
|
| 7 | Решение тригонометрических уравнений с последующим отбором корней. | Решать тригонометрические уравнения | 1 | 18.10 |
|
| 8 | Решение тригонометрических уравнений с последующим отбором корней. | Решать тригонометрические уравнения | 1 | 25.10 |
|
| 9 | Решение тригонометрических уравнений с последующим отбором корней. | Решать тригонометрические уравнения | 1 | 8.11 |
|
| 10 | Решение тригонометрических уравнений с последующим отбором корней. | Решать тригонометрические уравнения | 1 | 15.11 |
|
| 11 | Контрольная работа №2 «Решение тригонометрических уравнений с последующим отбором корней». |
| 1 | 22.11 |
|
| 12 | Производная и ее применение.
| Производная. | 1 | 29.11 |
|
| 13 | Физический и геометрический смысл производной | Производная. | 1 | 6.12 |
|
| 14 | Физический и геометрический смысл производной | Производная. | 1 | 13.12 |
|
| 15 | Производная и исследование функций. Возрастание и убывание функции. Экстремумы. | Производная. | 1 | 20.12 |
|
| 16 | Производная и исследование функций. Возрастание и убывание функции. Экстремумы. | Производная. | 1 | 27.12 |
|
| 17 | Контрольная работа № 3 по теме «Производная. Еефизический и геометрический смысл.Возрастание и убывание функции. Экстремумы».
|
| 1 | 17.01 |
|
| 18 | Чтение графиков функции и графиков производной функции | Производная.Чтение графиков функции и графиков производной функции | 1 | 24.01 |
|
| 19 | Чтение графиков функции и графиков производной функции | Производная.Чтение графиков функции и графиков производной функции | 1 | 31.01 |
|
| 20 | Наибольшее и наименьшее значение функции. | Производная.Чтение графиков функции и графиков производной функции | 1 | 7.02 |
|
| 21 | Наибольшее и наименьшее значение функции. | Чтение графиков функции и графиков производной функции | 1 | 14.02 |
|
| 22 | Контрольная работа № 4 по теме «Чтение графиков функции и графиков производной функции. Наибольшее и наименьшее значение функции». |
| 1 | 21.02 |
|
| 23 | Комбинаторика. Поочередный и одновременный выбор. Размещения с повторениями, сочетания с повторениями. Перестановки. | Комбинаторика. Поочередный и одновременный выбор. Размещения с повторениями, сочетания с повторениями. Перестановки. | 1 | 28.02 |
|
| 24 | Комбинаторика. Поочередный и одновременный выбор. Размещения с повторениями, сочетания с повторениями. Перестановки. | Комбинаторика. Поочередный и одновременный выбор. Размещения с повторениями, сочетания с повторениями. Перестановки. | 1 | 7.03 |
|
| 25 | Вероятность. Частота события, вероятность. Равновозможные события и подсчет их вероятности. | Вероятность. Частота события, вероятность. Равновозможные события и подсчет их вероятности. | 1 | 14.03 |
|
| 26 | Вероятность. Частота события, вероятность. Равновозможные события и подсчет их вероятности. | Вероятность. Частота события, вероятность. Равновозможные события и подсчет их вероятности. | 1 | 14.03 |
|
| 27 | Геометрическая вероятность. Вероятности событий. Условная вероятность. | Вероятность. Частота события, вероятность. Равновозможные события и подсчет их вероятности. | 1 | 21.03 |
|
| 28 | Геометрическая вероятность. Вероятности событий. Условная вероятность. | Вероятность. Частота события, вероятность. Равновозможные события и подсчет их вероятности. | 1 | 4.04 |
|
| 29 | Независимость событий. Вероятность произведения независимых событий. Формула Бернулли. | Понятие о независимости событий | 1 | 11.04 |
|
| 30 | Независимость событий. Вероятность произведения независимых событий. Формула Бернулли. | Понятие о независимости событий | 1 | 18.04 |
|
| 31 | Статистические данные. Представление данных в виде таблиц, диаграмм, графиков. Понятие о статистическом выводе на основе выборки | Табличное и графическое представление данных.Числовые характеристики рядов данных | 1 | 25.04 |
|
| 32 | Статистические данные. Представление данных в виде таблиц, диаграмм, графиков. Понятие о статистическом выводе на основе выборки | Табличное и графическое представление данных.Числовые характеристики рядов данных | 1 | 2.05 |
|
| 33 | Контрольная работа № 5 «Элементы комбинаторики, статистики и теории вероятностей». |
| 1 | 16.05 |
|
| 34 | Итоговый урок | Основное логарифмическое тождество. Логарифм произведения, частного, степени | 1 | 23.05 |
|
Материально-техническое обеспечение реализации программы
| Технические средства обучения |
| Компьютер PHILIPS, подключенный к сети Internet | 1 |
| ПроекторACER | 1 |
| Оборудование класса |
| Ученические столы одноместные с комплектом стульев. | 30+30 |
| Стол учительский с тумбой. | 1 |
| Стол компьютерный | 1 |
| Шкафы для хранения учебников, дидактических материалов, пособий и пр. | 6 |
| Настенная магнитная доска | 1 |
.
Литература для учителя:
Л.А. Александрова «Алгебра и начала математического анализа. 10 кл.: Самостоятельные работы: Учеб. пособие для общеобразоват. учреждений» / Л.А. Александрова; под ред. А.Г. Мордковича. – М.: Мнемозина, 2015. – 100с.
В.И. Глизбург «Алгебра и начала математического анализа. 11 класс. Контрольные работы для учащихся общеобразовательных учреждений (базовый уровень)» / В.И. Глизбург; под ред. А.Г. Мордковича. – М.: Мнемозина, 2015. – 32с.
Мордкович, А.Г., Семенов П.В. «Алгебра и начала математического анализа. 10-11 классы. Методическое пособие для учителя (базовый уровень)» - М.: Мнемозина, 2015.- 202 с.
Семенов А.Л., Ященко И.В. и др. «ЕГЭ 2014. Математика. Типовые тестовые задания» - М.: Издательство «Экзамен», 2015 -88с
Математика. Подготовка к ЕГЭ – 2015. Книга 1:учебно-методическое пособие/под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова. – Ростов-на-Дону: Легион, 2014., 98с.
Семенов, А.С. Трепалин, И.В. Ященко, П.И. Захаров, под ред. И.В. Ященко/ - М.: Интеллект-Центр, 2016. – 88с.
Оценочные материалы по учебному элективному курсу «Подготовка к ЕГЭ»
Контрольная работа №1 «Решение простейших геометрических уравнени
Вычислите: 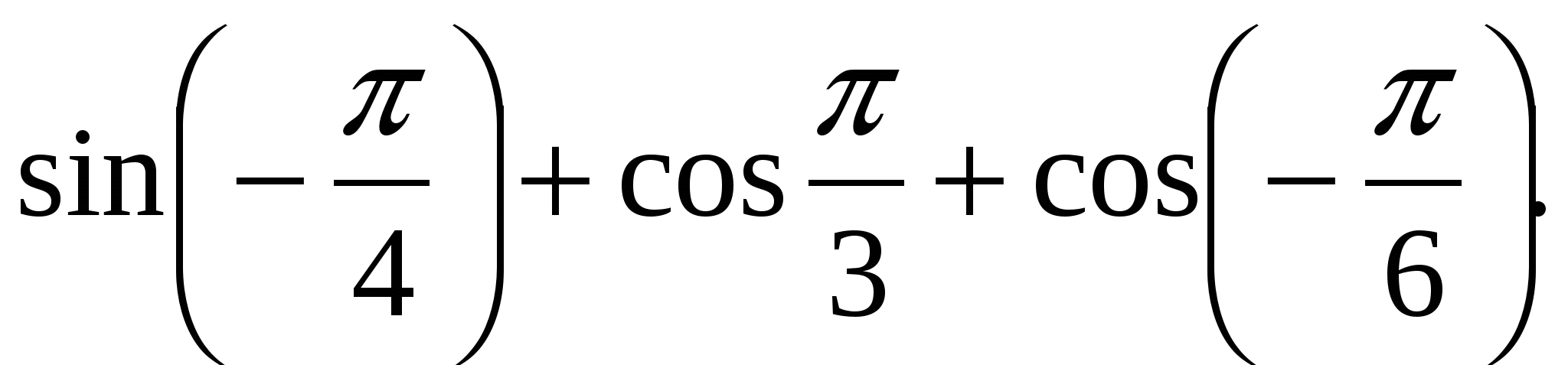
Вычислите с помощью формулы приведения: 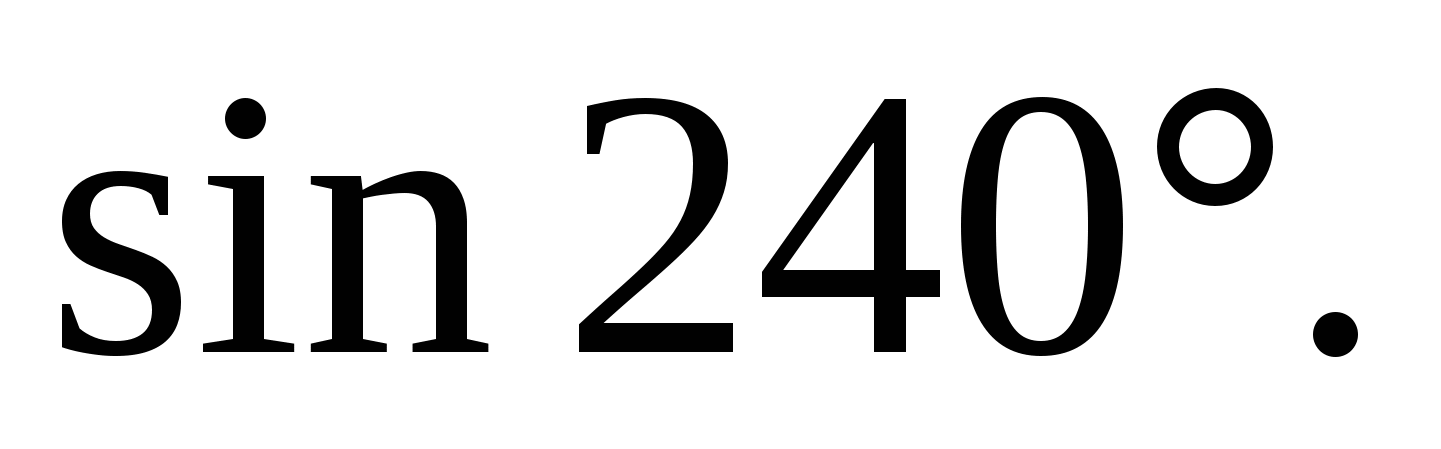
Решите графически уравнение: 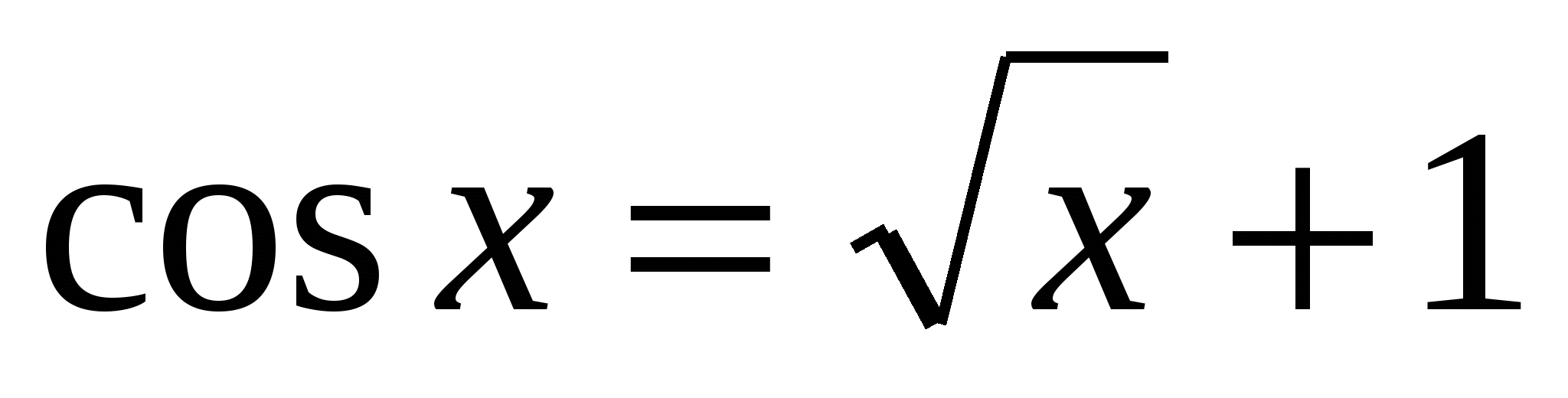
Решите уравнение: 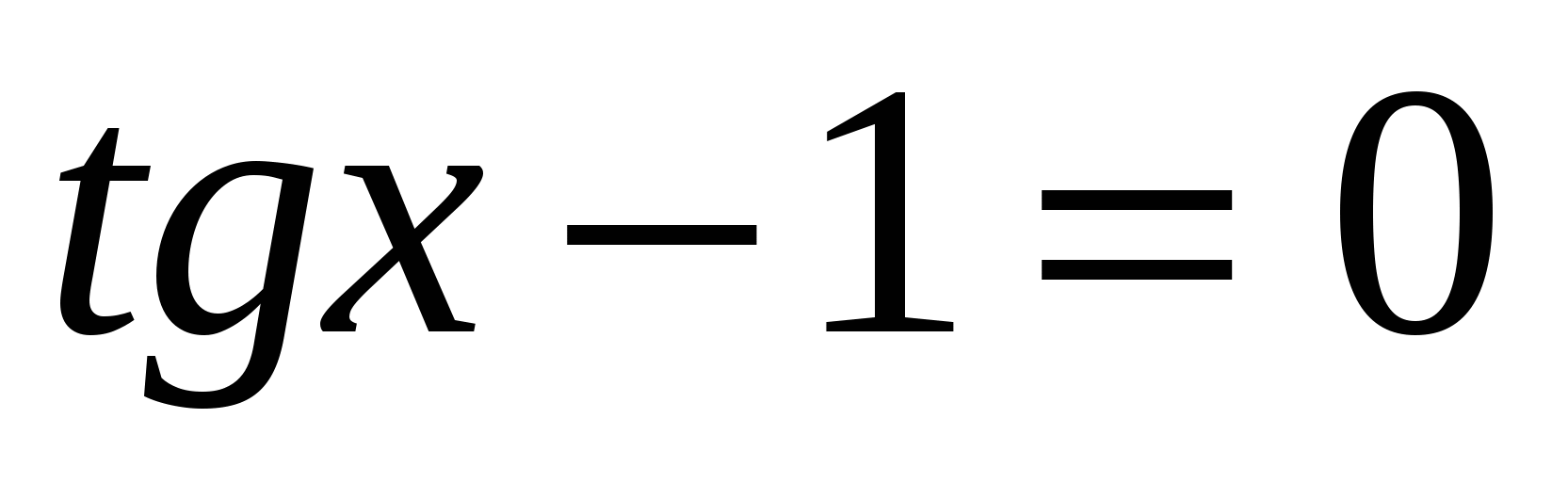
Решите уравнение: 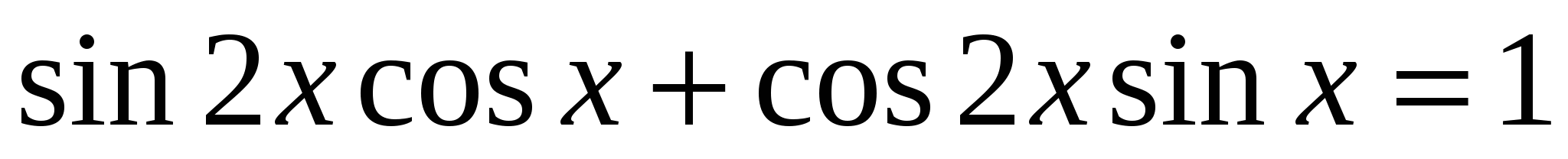
Докажите, что верно равенство: 
Решить уравнение: 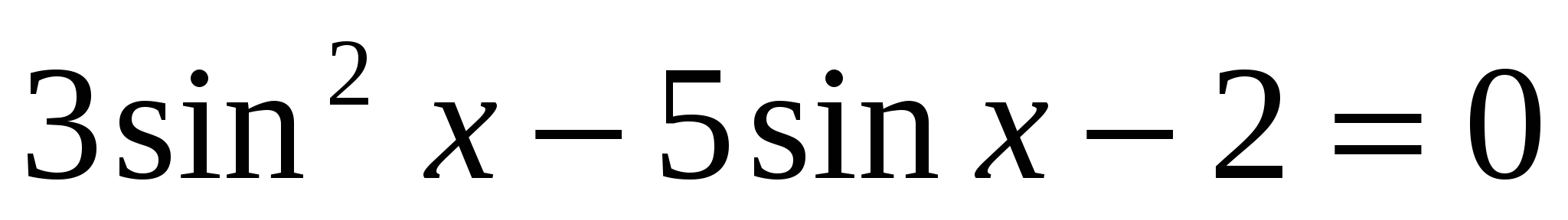
*Решить уравнение: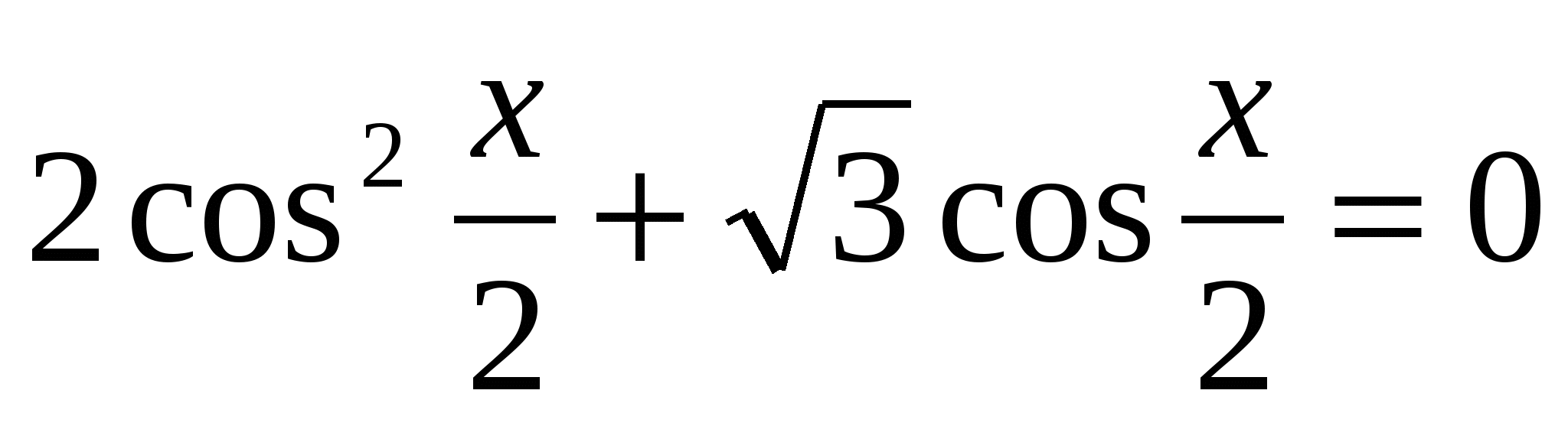
Контрольная работа №2 «Решение тригонометрических уравнений с последующим отбором корней».
1. а) Решите уравнение cos 2x + 3sin2x = 1,25.
б). Найдите все корни этого уравнения, принадлежащие отрезку 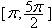 .
.
2. а). Решите уравнение cos2x – sin2(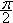 – x) = – 0,25.
– x) = – 0,25.
б). Найдите все корни этого уравнения, принадлежащие отрезку 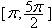 .
.
3. а) Решите уравнение sin2x = 2sinx – cosx + 1.
б). Найдите все корни этого уравнения, принадлежащие отрезку 
4. а) Решите уравнение 4cos2x + 4cos( 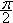 + x) – 1 = 0.
+ x) – 1 = 0.
б) Найдите все корни уравнения, принадлежащие отрезку 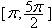
5. а) Решите уравнение 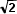 sin3x –
sin3x – 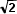 sinx + cos2x = 0.
sinx + cos2x = 0.
б) Найдите корни уравнения, принадлежащие промежутку [– 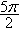 ; –
; –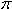 ].
].
Контрольная работа № 3 по теме «Производная. Ее физический и геометрический смысл. Возрастание и убывание функции. Экстремумы».
Найдите значение производной функции 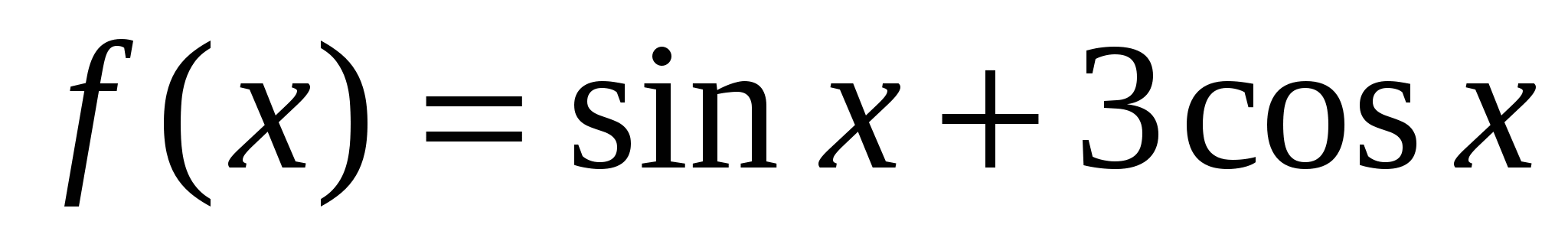 в точке
в точке 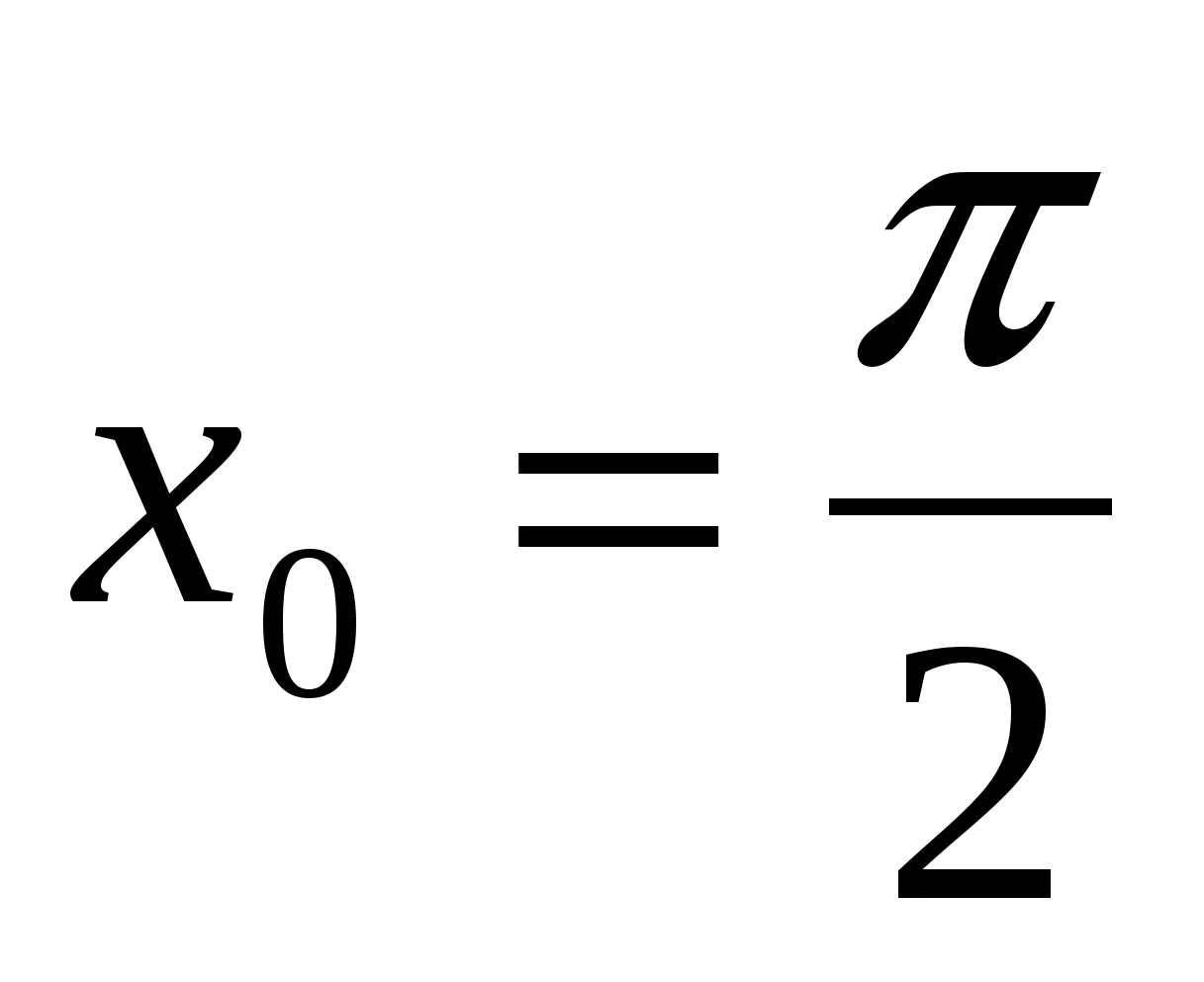 .
.
Найдите значение производной функции 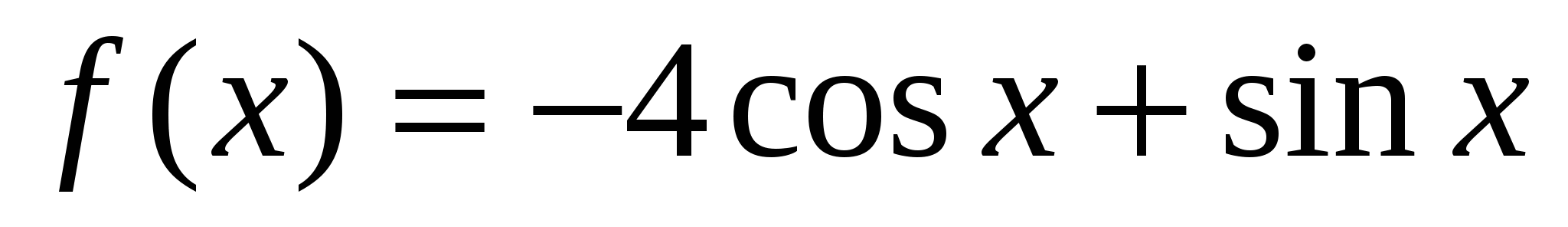 в точке
в точке 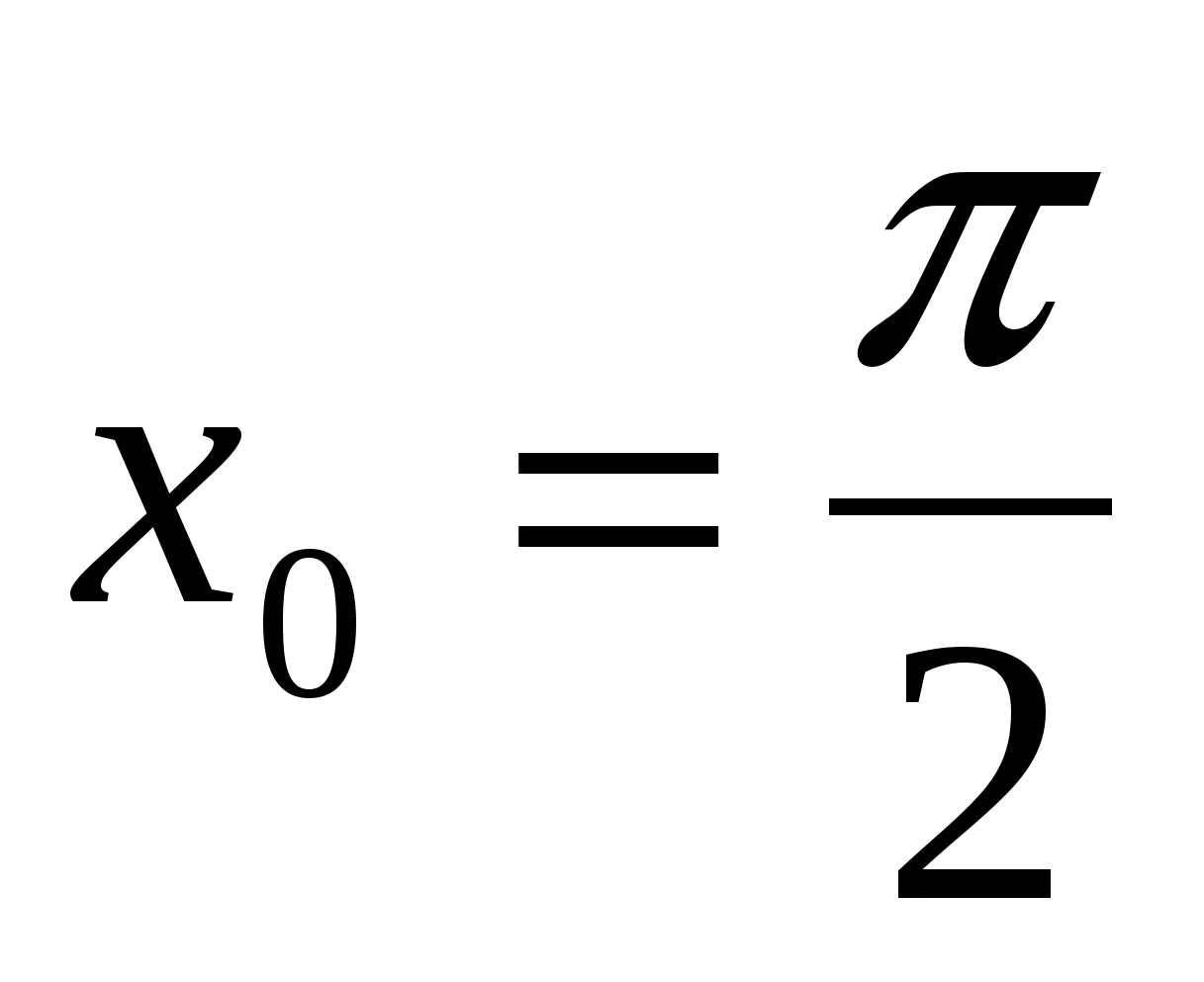 .
.
На рисунке изображён график функции 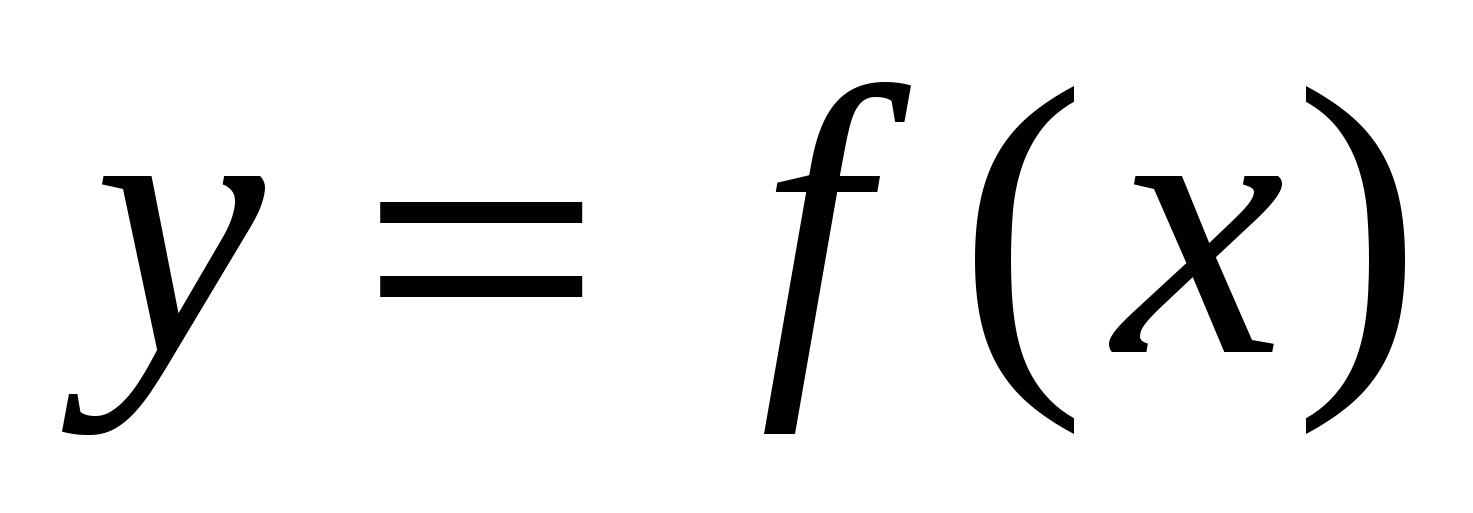 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой 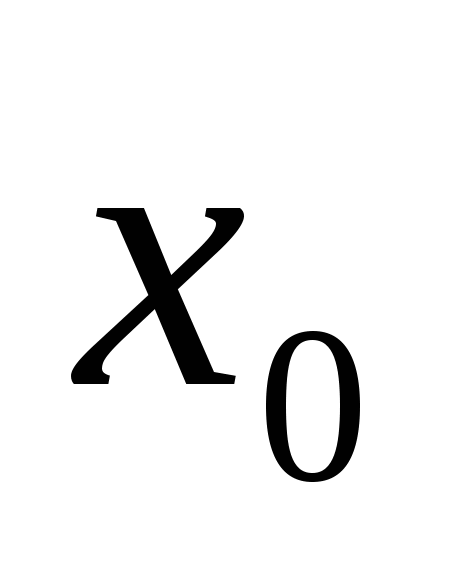 . Найдите значение производной функции в точке
. Найдите значение производной функции в точке 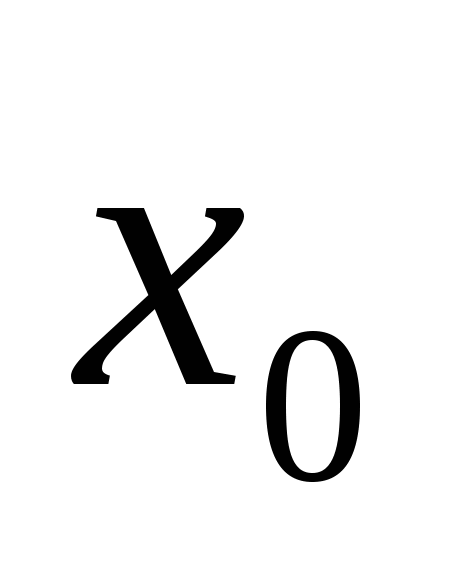 .
.
На рисунке изображён график функции 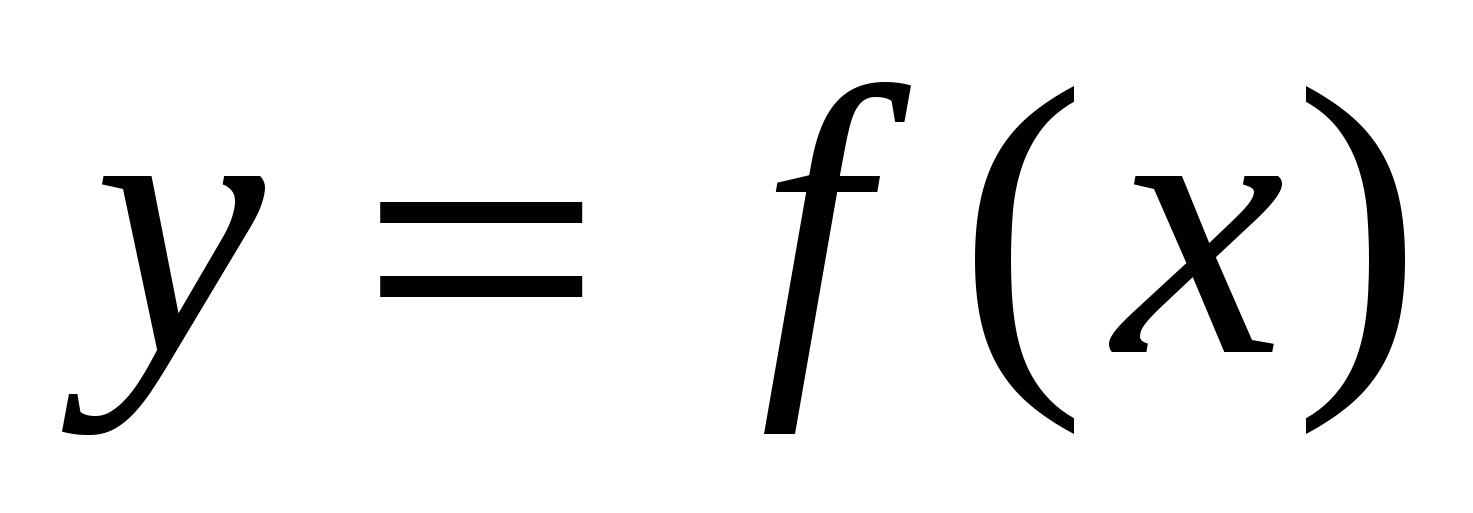 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой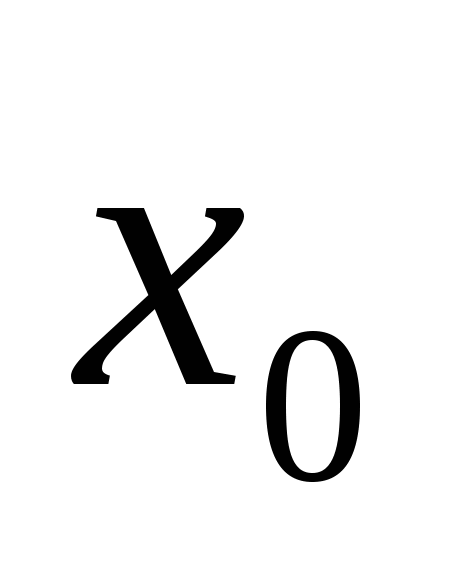 . Найдите значение производной функции в точке
. Найдите значение производной функции в точке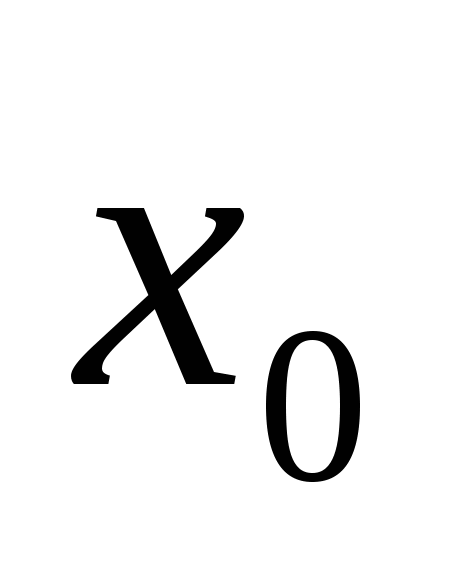 .
.
Найдите угловой коэффициент касательной к графику функции в точке с абсциссой .
Найдите угловой коэффициент касательной к графику функции в точке с абсциссой .
На рисунке изображен график функции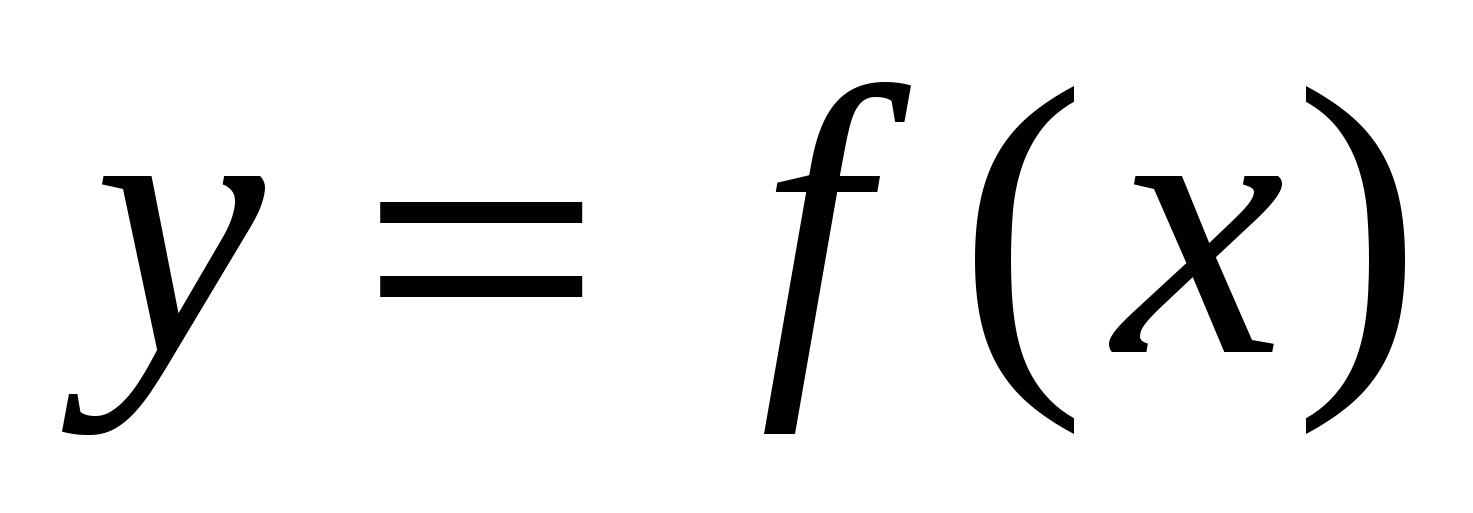 , определенной на интервале (-7;5).
, определенной на интервале (-7;5).
Найдите сумму точек экстремума функции.
Найдите точки минимума функции .
Найдите точки максимума функции .
7
Точка движется прямолинейно по закону . Вычислите скорость и ускорение точки при t = 1.
Точка движется прямолинейно по закону . Вычислите скорость и ускорение точки при t = 1.
Контрольная работа № 4 по теме «Чтение графиков функции и графиков производной функции.
Наибольшее и наименьшее значение функции».
На рисунке изображен график производной функции, определенной на интервале(-8; 4).
В какой точке отрезка функция принимает наименьшее значение.
На рисунке изображен график производной функции, определенной на интервале(-8;3). В какой точке отрезка функция принимает наибольшее значение.
На рисунке изображен график функции  , определенной на интервале
, определенной на интервале  . Определите количество целых точек, в которых производная функции положительна.
. Определите количество целых точек, в которых производная функции положительна.
На рисунке изображен график  — производной функции
— производной функции  , определенной на интервале
, определенной на интервале  . В какой точке отрезка
. В какой точке отрезка  функция
функция  принимает наибольшее значение?
принимает наибольшее значение?
На рисунке изображен график  — производной функции
— производной функции  , определенной на интервале
, определенной на интервале  . Найдите промежутки возрастания функции
. Найдите промежутки возрастания функции  . В ответе укажите сумму целых точек, входящих в эти промежутки.
. В ответе укажите сумму целых точек, входящих в эти промежутки.
На рисунке изображен график  — производной функции
— производной функции  , определенной на интервале
, определенной на интервале  . Найдите промежутки убывания функции
. Найдите промежутки убывания функции  . В ответе укажите длину наибольшего из них.
. В ответе укажите длину наибольшего из них.
Контрольная работа № 5 « Элементы комбинаторики, статистики и теории вероятностей».
Ответ: 0,16.
Ответ: 0,16
285922
0,16
Конкурс исполнителей проводится в 5 дней. Всего заявлено 80 выступлений — по одному от каждой страны, участвующей в конкурсе. Исполнитель из России участвует в конкурсе. В первый день запланировано 8 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление исполнителя из России состоится в третий день конкурса?
Решение.
На третий день запланировано выступлений. Значит, вероятность того, что выступление представителя из России окажется запланированным на третий день конкурса, равна
Ответ: 0,225.
Ответ: 0,225
285923
0,225
На конференцию приехали 3 ученых из Норвегии, 3 из России и 4 из Испании. Каждый из них делает на конференции один доклад. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что восьмым окажется доклад ученого из России.
Решение.
Всего в семинаре принимает участие 3 + 3 + 4 = 10 ученых, значит, вероятность того, что ученый, который выступает восьмым, окажется из России, равна 3/10 = 0,3.
Ответ: 0,3.
Ответ: 0,3
285924
0,3
Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 спортсменов из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России.
Решение.
В первом туре Руслан Орлов может сыграть с 26 − 1 = 25 бадминтонистами, из которых 10 − 1 = 9 из России. Значит, вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России, равна
Ответ: 0,36.
Ответ: 0,36
285925
0,36
В сборнике билетов по биологии всего 55 билетов, в 11 из них встречается вопрос по теме "Ботаника". Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме "Ботаника".
Решение.
Вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по ботанике, равна
Ответ: 0,2.
Ответ: 0,2
285926
0,2
В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по теме "Неравенства". Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по теме "Неравенства".
Решение.
Из 25 билетов 15 не содержат вопроса по теме "Неравенства", поэтому вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по теме "Неравенства", равна
Ответ: 0,6.
Ответ: 0,6
285927
0,6
Вася, Петя, Коля и Лёша бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет Петя.
Решение.
Жребий начать игру может выпасть каждому из четырех мальчиков. Вероятность того, что это будет именно Петя, равна одной четвертой.
1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4.
Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?
Решение.
Вероятность того, что команда России окажется во второй группе, равна отношению количества карточек с номером 2, к общему числу карточек. Тем самым, она равна
Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже чем 36,8 °С, равна 0,81. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36,8 °С или выше.
Решение.
Указанные события противоположны, поэтому искомая вероятность равна 1 − 0,81 = 0,19.
Ответ: 0,19.
Ответ: 0,19
320197
0,19
При изготовлении подшипников диаметром 67 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,965. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 66,99 мм или больше чем 67,01 мм.
Решение.
По условию, диаметр подшипника будет лежать в пределах от 66,99 до 67,01 мм с вероятностью 0,965. Поэтому искомая вероятность противоположного события равна 1 − 0,965 = 0,035.
Ответ: 0,035.
Ответ: 0,035
320196
0,035
Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
Решение.
Поскольку биатлонист попадает в мишени с вероятностью 0,8, он промахивается с вероятностью 1 − 0,8 = 0,2. Cобытия попасть или промахнуться при каждом выстреле независимы, вероятность произведения независимых событий равна произведению их вероятностей. Тем самым, вероятность события «попал, попал, попал, промахнулся, промахнулся» равна

Ответ: 0,02.
Ответ: 0,02
320173
0,02
Помещение освещается фонарём с двумя лампами. Вероятность перегорания лампы в течение года равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Решение.
Найдем вероятность того, что перегорят обе лампы. Эти события независимые, вероятность их произведения равно произведению вероятностей этих событий: 0,3·0,3 = 0,09.
Событие, состоящее в том, что не перегорит хотя бы одна лампа, противоположное. Следовательно, его вероятность равна 1 − 0,09 = 0,91.
Ответ: 0,91.
Ответ: 0,91
320175
0,91
При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем — 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?В ответе укажите наименьшее необходимое количество выстрелов.
Решение.
Найдем вероятность противоположного события, состоящего в том, что цель не будет уничтожена за n выстрелов. Вероятность промахнуться при первом выстреле равна 0,6, а при каждом следующем — 0,4. Эти события независимые, вероятность их произведения равна произведению вероятности этих событий. Поэтому вероятность промахнуться при n выстрелах равна: 
Последовательно проверяя значения  , равные 1, 2, 3 и т. д. находим, что искомым решением является
, равные 1, 2, 3 и т. д. находим, что искомым решением является  . Следовательно, необходимо сделать 5 выстрелов.
. Следовательно, необходимо сделать 5 выстрелов.
Р(1) = 0,6.
Р(2) = Р(1)·0,4 = 0,24.
Р(3) = Р(2)·0,4 = 0,096.
Р(4) = Р(3)·0,4 = 0,0384;
Р(5) = Р(4)·0,4 = 0,01536.
Приведем другое решение.
Вероятность поразить мишень равна сумме вероятностей поразить ее при первом, втором, третьем и т. д. выстрелах. Поэтому задача сводится к нахождению наименьшего натурального решения неравенства
В нашем случае неравенство решается подбором, в общем случае понадобится формула суммы геометрической прогрессии, использование которой сведет задачу к простейшему логарифмическому неравенству.
Ответ: 5
320187
5
На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос по теме «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение.
Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: 0,2 + 0,15 = 0,35.
Ответ: 0,35.
Ответ: 0,35
320171
0,35
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4.
Решение.
Команда может получить не меньше 4 очков в двух играх тремя способами: 3+1, 1+3, 3+3. Эти события несовместны, вероятность их суммы равна сумме их вероятностей. Каждое из этих событий представляет собой произведение двух независимых событий — результата в первой и во второй игре. Отсюда имеем:


Ответ: 0,32.
Ответ: 0,32
320188
0,32
В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.
Решение.
Для погоды на 4, 5 и 6 июля есть 4 варианта: ХХО, ХОО, ОХО, ООО (здесь Х — хорошая, О — отличная погода). Найдем вероятности наступления такой погоды:
P(XXO) = 0,8·0,8·0,2 = 0,128;
P(XOO) = 0,8·0,2·0,8 = 0,128;
P(OXO) = 0,2·0,2·0,2 = 0,008;
P(OOO) = 0,2·0,8·0,8 = 0,128.
P(ХХО) + P(ХОО) + P(ОХО) + P(ООО) = 0,128 + 0,128 + 0,008 + 0,128 = 0,392.
Ответ: 0,392
320206
0,392
В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Решение.
Найдем вероятность того, что неисправны оба автомата. Эти события независимые, вероятность их произведения равна произведению вероятностей этих событий: 0,05 · 0,05 = 0,0025.
Событие, состоящее в том, что исправен хотя бы один автомат, противоположное. Следовательно, его вероятность равна 1 − 0,0025 = 0,9975.
Приведем другое решение.
Вероятность того, что исправен первый автомат (событие А) равна 0,95. Вероятность того, что исправен второй автомат (событие В) равна 0,95. Это совместные независимые события. Вероятность их произведения равна произведению вероятностей этих событий, а вероятность их суммы равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения. Имеем:
P(A + B) = P(A) + P(B) − P(A·B) = P(A) + P(B) − P(A)P(B) = 0,95 + 0,95 − 0,95·0,95 = 0,9975.
Ответ: 0,9975
320174
0,9975
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Решение.
Рассмотрим события
А = кофе закончится в первом автомате,
В = кофе закончится во втором автомате.
Тогда
A·B = кофе закончится в обоих автоматах,
A + B = кофе закончится хотя бы в одном автомате.
По условию P(A) = P(B) = 0,3; P(A·B) = 0,12.
События A и B совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения:
P(A + B) = P(A) + P(B) − P(A·B) = 0,3 + 0,3 − 0,12 = 0,48.
Следовательно, вероятность противоположного события, состоящего в том, что кофе останется в обоих автоматах, равна 1 − 0,48 = 0,52.
Приведем другое решение.
Вероятность того, что кофе останется в первом автомате равна 1 − 0,3 = 0,7. Вероятность того, что кофе останется во втором автомате равна 1 − 0,3 = 0,7. Вероятность того, что кофе останется в первом или втором автомате равна 1 − 0,12 = 0,88. Поскольку P(A + B) = P(A) + P(B) − P(A·B), имеем: 0,88 = 0,7 + 0,7 − х, откуда искомая вероятость х = 0,52.
Примечание.
Заметим, что события А и В не являются независимыми. Действительно, вероятность произведения независимых событий была бы равна произведению вероятностей этих событий: P(A·B) = 0,3·0,3 = 0,09, однако, по условию, эта вероятность равна 0,12.
Ответ: 0,52
320172
0,52
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая — 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Решение.
Вероятность того, что стекло сделано на первой фабрике и оно бракованное: 0,45 · 0,03 = 0,0135.
Вероятность того, что стекло сделано на второй фабрике и оно бракованное: 0,55 · 0,01 = 0,0055.
Поэтому по формуле полной вероятности вероятность того, что случайно купленное в магазине стекло окажется бракованным равна 0,0135 + 0,0055 = 0,019.
Ответ: 0,019.
Ответ: 0,019
319353
0,019
Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.

















