МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 61
ИМЕНИ М.И.НЕДЕЛИНА Г.ЛИПЕЦКА
| «Согласовано» Руководитель МО ________ / Вовденко О.Л./
Протокол № ___ от «__»_________201___г.
| «Согласовано» Зам. директора школы по УВР МБОУ СОШ № 61 __________ / Степанова Е.Н./
«__»__________201___г.
|
РАБОЧАЯ ПРОГРАММА
по математике
9 класс
(с углубленным изучением математики)
Рассмотрено на заседании
педагогического совета
протокол № ____
от «__»_______201___ г.
Пояснительная записка
Рабочая программа учебного курса математики для 9-х классов (с углубленным изучением математики) основной общеобразовательной школы составлена на основе авторских программ:
курса алгебры Мордковича А.Г. (Программы. Математика. 5-6 кл. Алгебра. 7-9 кл. Алгебра и начала математического анализа. 10-11 кл./авт.-сост. И.И. Зубарева, А.Г. Мордкович)
курса геометрии Атанасяна Л.С. (Сборник рабочих программ. Геометрия. 7 - 9 кл.: пособие для учителей общеобразовательных учреждений /Сост. Т.А. Бурмистрова).
Изучение курса математики ориентировано на использование учебников «Алгебра – 9» (авт. А.Г. Мордкович, Н.П. Николаев), «Геометрия 7-9» (авт. Л.С. Атанасян), рекомендованных Министерством образования и науки Российской Федерации.
Согласно федеральному базисному учебному плану на изучение математики в 9 классе отводится не менее 175 часов (5 часов в неделю, 35 учебных недель). Учебным планом школы на 2015-2016 уч. год на изучение математики в 9 классе (с углубленным изучением математики) выделено 7 часов в неделю (35 недель, 245 часов за год).
Курс математики состоит из следующих предметов: «Алгебра», «Геометрия». Изучение программного материала предполагается в виде блоков. В соответствии с этим составлено тематическое планирование.
В основу курса математики положены такие принципы как:
целостность и непрерывность, означающие, что данная ступень является важным звеном единой общешкольной подготовки по математике;
научность в сочетании с доступностью, строгость и систематичность изложения (включение в содержание фундаментальных положений современной науки с учетом возрастных особенностей обучаемых);
практико-ориентированность, обеспечивающая отбор содержания, направленного на решение простейших практических задач планирования деятельности, поиска нужной информации;
принцип развивающего обучения (обучение ориентировано не только на получение новых знаний, но и активизацию мыслительных процессов, формирование и развитие у школьников обобщенных способов деятельности, формирование навыков самостоятельной работы).
Изучение математики на ступени основного общего образования направлено на достижение следующих целей:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
Формы работы: фронтальная, индивидуальная, коллективная, парная, групповая работа.
Методы работы: рассказ, объяснение, лекция, беседа, применение наглядных пособий, дифференцированные задания, самостоятельная работа, взаимопроверка, самопроверка, дидактическая игра, решение проблемно-поисковых задач.
Используются следующие формы и методы контроля усвоения материала: устный контроль (индивидуальный опрос, устная проверка знаний), письменный контроль (контрольные работы, самостоятельные работы, графические диктанты, тесты), проверка домашнего задания.
Учебный процесс осуществляется в классно-урочной форме в виде комбинированных, контрольно-проверочных и др. типов уроков.
Результаты обучения представлены в Требованиях к уровню подготовки и задают систему итоговых результатов обучения, которых должны достигать все учащиеся, и достижение которых является обязательным условием положительной аттестации ученика.
Уровень обучения – профильный.
Содержание тем учебного курса «Математика»
9 класс (с углубленным изучением математики)
Повторение курса 8 класса.
Рациональные выражения. Разложение многочлена на множители. Алгебраические дроби. Действия над алгебраическими дробями. Решение линейных и квадратных уравнений. Решение систем уравнений. Преобразование выражений, содержащих операцию извлечения квадратного корня. Треугольники, четырехугольники. Окружность.
Неравенства с одной переменной. Системы и совокупности неравенств.
Линейные и квадратные неравенства. Решение рациональных неравенств. Множества и операции над ними. Решение систем рациональных неравенств.
Знать:
терминологию, символику и свойства линейных, квадратных и рациональных неравенств;
терминологию, символику и свойства множеств;
алгоритмы решения неравенств и их систем;
терминологию, символику и метод решения систем линейных и квадратных неравенств.
совокупности неравенств;
неравенства с модулями;
иррациональные неравенства;
задачи с параметрами.
Уметь:
решать линейные, квадратные и рациональные неравенства, системы неравенств с одной переменной;
применять аппарат неравенств для решения задач из различных разделов математики;
приводить примеры конечных и бесконечных множеств;
задавать множества;
производить операции над множествами
В ходе изучения темы проводится контрольная работа № 1 «Неравенства с одной переменной» и № 2 «Системы и совокупности неравенств».
Векторы
Понятие вектора. Длина (модуль) вектора. Сонаправленные отрезки и векторы. Равенство векторов. Откладывание вектора от данной точки. Операции над векторами: умножение на число, сложение и вычитание, разложение. Применение векторов к решению задач. Средняя линия трапеции.
Знать:
определение вектора, длины вектора, коллинеарных векторов, равных векторов;
правила и законы сложения, вычитания векторов и умножения вектора на число;
теорему о средней линии трапеции.
Уметь:
вычислять длину вектора;
выполнять операции над векторами;
использовать векторный метод при решении задач на вычисления и доказательство.
В ходе изучения темы проводится контрольная работа № 3 «Векторы»
Системы уравнений
Уравнение с двумя переменными, его уравнение и график. Системы рациональных уравнений, основные методы их решения: графический, подстановка, алгебраическое сложение, введение новых переменных. Понятие о равносильности систем уравнений. Системы уравнений как математические модели реальных ситуаций (текстовые задачи).
Знать:
терминологию рациональных уравнений и неравенств с двумя переменными;
формулу расстояния между двумя точками и уравнение окружности;
терминологию систем рациональных уравнений и неравенств с двумя переменными;
алгоритмы решения систем уравнений.
однородные системы. Симметрические системы.
иррациональные системы. Системы с модулями.
системы уравнений как математические модели реальных ситуаций.
Уметь:
решать задачи, алгебраической моделью которых является уравнение с двумя переменными; находить целые решения путем перебора;
решать системы двух уравнений, одно из которых линейное, а другое – второй степени; решать системы нелинейных уравнений;
решать текстовые задачи алгебраическим способом: переходить от словесной формулировки условия задачи к алгебраической модели путем составления системы уравнений; решать составленную систему уравнений; интерпретировать результат;
строить графики уравнений с двумя переменными. Конструировать эквивалентные речевые высказывания с использованием алгебраического и геометрического языков;
решать и исследовать уравнения и системы уравнений на основе функционально-графических представлений уравнений.
Контрольные работы № 4 и № 5 «Системы уравнений»
Метод координат
Координаты вектора. Простейшие задачи в координатах. Уравнение линии на плоскости. Уравнение окружности. Уравнение прямой.
Знать:
понятие прямоугольной системы координат, координат точки и координат вектора;
формулы координат середины отрезка, расстояния между двумя точками плоскости, уравнения прямой и окружности.
Уметь:
находить для векторов, заданных координатами: длину вектора, координаты суммы и разности двух и более векторов, координаты произведения вектора на число, применяя при необходимости сочетательный, переместительный и распределительный законы;
вычислять длину отрезка по координатам его концов, вычислять координаты середины отрезка;
использовать координатный метод для изучения свойств прямых и окружностей;
использовать координатный метод при решении задач на вычисления и доказательство.
В ходе изучения темы проводится контрольная работа № 6 «Метод координат»
Числовые функции
Определение функции, способы задания функции. Область определения, область значений функции. Свойства функций: монотонность, ограниченность, наименьшее и наибольшее значения функции на заданном промежутке. Четные и нечетные функции, особенности их графиков. Наглядно-геометрические представления о непрерывности и выпуклости функций. Функции у=хп, у=х-п, (n-натуральное число), у= 3√ х их свойства и графики. Построение графика кусочно-заданной функции.
Знать:
функциональные понятия и язык (термины, символические обозначения);
определения функций у=хп, у=х-п, (n-натуральное число), у= 3√ х их свойства и графики.
Уметь:
вычислять значения функций, заданных формулами; составлять таблицы значений функций;
находить значения кубических корней, при необходимости используя калькулятор;
строить по точкам графики функций. Описывать свойства функций на основе ее графического представления;
моделировать реальные зависимости формулами и графиками. Читать графики реальных зависимостей;
использовать функциональную символику для записи разнообразных фактов, связанных с рассматриваемыми функциями. Строить речевые конструкции с использованием функциональной терминологии;
распознавать виды изучаемых функций. Показывать схематически положение на координатной плоскости графиков функций y=kx, y=kx+b,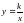 ,
, 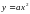 ,
, 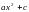 ,
, 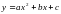 в зависимости от значений коэффициентов;
в зависимости от значений коэффициентов;
строить графики изучаемых функций; описывать их свойства.
В ходе изучения темы проводятся контрольная работа № 7 «Способы задания функции. Свойства функций» и контрольная работа № 8 «Числовые функции»
Соотношение между сторонами и углами треугольника
Синус, косинус, тангенс угла. Основное тригонометрическое тождество. Формулы приведения. Формулы для вычисления координат точки. Теорема о площади треугольника. Теорема синусов. Теорема косинусов. Решение треугольников. Скалярное произведение векторов и его свойства. Скалярное произведение в координатах. Применение скалярного произведения векторов при решении задач и доказательстве теорем.
Знать:
определения синуса, косинуса, тангенса, котангенса углов от 0º до 180º;
формулы, выражающие функции углов от 0º до 180º через функции острых углов;
основное тригонометрическое тождество;
теоремы синусов и косинусов;
формулу, выражающую площадь треугольника через две стороны и угол между ними;
определение угла между векторами;
определение и теорему о скалярном произведении векторов.
Уметь:
оперировать с начальными понятиями тригонометрии и выполнять операции над функциями углов;
вычислять площади треугольников;
вычислять скалярное произведение векторов, находить угол между векторами, устанавливать перпендикулярность прямых;
решать практические задачи, связанные с нахождением геометрических величин (используя при необходимости справочники и технические средства).
В ходе изучения темы проводится контрольная работа № 9 «Соотношения между сторонами и углами треугольника»
Прогрессии
Определение числовой последовательности и способы ее задания: аналитический, словесный, рекуррентный. Монотонные последовательности. Арифметическая и геометрическая прогрессии: определения, формулы n-го члена, формулы суммы n членов, характеристические свойства. Метод математической индукции.
Знать:
язык последовательностей (термины, символические обозначения);
формулы, связанные с арифметической и геометрической прогрессией.
В чём заключается метод математической индукции.
Уметь:
вычислять члены последовательности, заданных формулой n-го члена или рекуррентной формулой. Устанавливать закономерность в построении последовательности, если выписаны несколько ее членов. Изображать члены последовательности точками на координатной плоскости;
распознавать арифметическую и геометрическую прогрессии при разных способах задания. Выводить на основе доказательных рассуждений формулы общего члена арифметической и геометрической прогрессий, суммы n первых членов арифметической и геометрической прогрессий; решать задачи с использованием этих формул;
рассматривать примеры из реальной жизни, иллюстрирующие изменения в арифметической прогрессии, в геометрической прогрессии; изображать соответствующие зависимости графически;
решать задачи на сложные проценты, в том числе задачи из реальной практики (с использованием калькулятора).
В ходе изучения темы проводятся контрольные работы № 10 и № 11 «Прогрессии»
Длина окружности и площадь круга
Правильные многоугольники и их свойства. Окружность, описанная около правильного многоугольника. Окружность, вписанная в правильный многоугольник. Формулы для нахождения площади и стороны правильного многоугольника, радиуса окружности. Длина окружности. Длина дуги окружности. Площади круга, сектора, сегмента.
Знать:
определение и приводить примеры правильных многоугольников;
определения вписанных и описанных многоугольников;
теоремы о вписанной и описанной окружностях многоугольника;
формулы для вычисления площади правильного многоугольника, его стороны, и радиуса вписанной окружности.
понятие длины окружности и площади круга;
формулы длины окружности и площади круга, соответствие между величиной центрального угла и длиной дуги окружности.
Уметь:
распознавать и изображать на чертежах и рисунках правильные многоугольники, окружность, круговой сектор;
решать несложные задачи на построение, применяя основные алгоритмы построения с помощью циркуля и линейки;
использовать свойства измерения длин, площадей и углов при решении задач на нахождение длины окружности, длины дуги окружности, градусной меры угла;
вычислять длину окружности, длину дуги окружности;
вычислять площадь круга, и сектора;
вычислять длины линейных элементов фигур и их углов, используя формулы длины окружности и длины дуги окружности, формулы площадей круга и сектора;
вычислять площади фигур, составленных из двух и более прямоугольников, параллелограммов, треугольников, круга и сектора.
В ходе изучения темы проводится контрольная работа № 12 «Длина окружности и площадь круга»
Элементы комбинаторики, статистики и теории вероятностей
Простейшие комбинаторные задачи. Правило умножения и дерево вариантов. Перестановки. Выбор нескольких элементов. Статистика: дизайн информации. Варианты и их кратности. Числовые характеристики данных измерения. Классическое определение вероятности. Случайные события и их вероятности. Экспериментальные данные и вероятности событий.
Знать:
правило комбинаторного умножения;
терминологию и методы обработки информации;
числовые характеристики данных измерений;
классическую вероятностную схему.
Уметь:
выполнять перебор всех возможных вариантов для пересчета объектов или комбинаций;
применять правило комбинаторного умножения для решения задач на нахождение числа объектов или комбинаций;
распознавать задачи на определение числа перестановок и выполнять соответствующие вычисления;
решать задачи на вычисление вероятности с применением комбинаторики;
извлекать информацию из таблиц и диаграмм, выполнять вычисления по табличным данным. Определять по диаграммам наибольшие и наименьшие данные, сравнивать величины;
представлять информацию в виде таблиц и диаграмм;
приводить примеры числовых данных, находить среднее арифметическое, размах, дисперсию числовых наборов;
приводить содержательные примеры использования средних и дисперсии для описания данных;
проводить случайные эксперименты, в том числе с помощью компьютерного моделирования, интерпретировать их результаты. Вычислять частоту случайного события; оценивать вероятность с помощь частоты, полученной опытным путем;
решать задачи на нахождение вероятностей событий;
приводить примеры случайных событий, в частности достоверных и невозможных событий, маловероятных событий. Приводить примеры равновероятных событий.
В ходе изучения темы проводится контрольная работа № 13 «Элементы комбинаторики, статистики и теории вероятностей»
Движение
Понятие движения. Параллельный перенос, поворот. Использование движения при решении задач.
Знать:
что такое отображение плоскости на себя и в каком случае оно называется движением;
что такое параллельный перенос и поворот;
основные виды движений.
Уметь:
строить равные и симметричные фигуры;
выполнять параллельный перенос и поворот;
применять идеи движения при решении геометрических задач.
В ходе изучения темы проводится контрольная работа № 14 «Движение»
Об аксиомах планиметрии. Начальные сведения из стереометрии
Аксиоматическое построение геометрии. Многогранники. Тела и поверхности вращения.
Знать:
аксиомы планиметрии;
что такое многогранник, его грани, ребра, вершины, диагонали, какой многогранник называется выпуклым;
понятия призмы, пирамиды, цилиндра, конуса, шара, свойства диагоналей параллелепипеда;
понятие объема тела и его свойства;
формулы площади поверхности и объемов тел.
Уметь:
решать задачи на построение и вычисления;
моделировать условие задачи с помощью чертежа или рисунка.
Итоговое повторение
Алгебраические выражения. Функции и графики. Уравнения и системы уравнений. Неравенства и системы неравенств. Степень с целым показателем и её свойства. Арифметический квадратный корень и его свойства. Арифметическая и геометрическая прогрессии. Решение текстовых задач выделением трех этапов математического моделирования. Параллельные прямые. Треугольники. Окружность. Четырёхугольники, многоугольники. Векторы. Метод координат. Итоговая контрольная работа по материалам ОГЭ.
Учебно-тематическое планирование курса «Математики», 9 класс
Количество часов: всего 245 часов, в неделю 7 часов
Плановых контрольных уроков: 14
Административных контрольных уроков: 3
Планирование составлено на основе: Программы. Математика. 5-6 кл. Алгебра. 7-9 кл. Алгебра и начала математического анализа. 10-11 кл./авт.-сост. И.И. Зубарева, А.Г. Мордкович. – М.: Мнемозина, 2011
Сборник рабочих программ. Геометрия. 7 - 9 кл.: пособие для учителей общеобразоват. учреждений /Сост. Т.А. Бурмистрова. - М.: Просвещение, 2011
Учебники: А.Г.Мордкович, Н.П. Николаев. Алгебра-9. Ч.1.Учебник. – М.: Мнемозина, 2014
А.Г.Мордкович, Л.И.Звавич, А.Р.Рязановский, Л.А. Александрова. Алгебра-9.Ч.2. Задачник. – М.: Мнемозина, 2014
Геометрия: Учеб. Для 7-9 кл. общеобразоват. учреждений/Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. – М.:Просвещение, 2010
| № п/п | Наименование разделов и тем | 7 ч/нед. | 6 ч/нед. |
| 1 | Повторение курса 8 класса | 9 | 9 |
| 2 | Рациональные неравенства и их системы | 22 | 22 |
| 3 | Векторы | 12 | 12 |
| 4 | Системы уравнений | 27 | 25 |
| 5 | Метод координат | 12 | 12 |
| 6 | Числовые функции | 25 | 23 |
| 7 | Соотношение между сторонами и углами треугольника | 16 | 16 |
| 8 | Прогрессии | 27 | 25 |
| 9 | Длина окружности и площадь круга | 13 | 13 |
| 10 | Элементы комбинаторики, статистически и теории вероятностей | 16 | 14 |
| 11 | Движение | 9 | 9 |
| 12 | Об аксиомах планиметрии. Начальные сведения из стереометрии | 9 | 9 |
| 13 | Итоговое повторение | 34 | 21 |
| 14 | Резерв | 14 | - |
|
| Итого | 245 | 210 |
Требования к уровню подготовки выпускников 9 классов
Учащиеся должны знать/понимать:
– значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
– значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
– универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности; вероятностный характер различных процессов окружающего мира;
-определение вектора и равных векторов;
- правила сложения, вычитания векторов, умножения вектора на число;
-понятия координат вектора, координат суммы и разности векторов, произведения вектора на число;
-формулы координат вектора через координаты его конца и начала, координат середины отрезка, длины вектора и расстояния между двумя точками;
-уравнения окружности и прямой;
-определения синуса, косинуса и тангенса углов от 0 до 180 , основное тригонометрическое тождество, формулы приведения;
-формулировку теоремы синусов и теоремы косинусов;
-способы решения треугольников;
-формулы длины окружности и ее дуги, площади круга и кругового сектора;
-все виды движений: симметрия, параллельный поворот, перенос;
должны уметь:
– выполнять арифметические действия, сочетая устные и письменные приемы; находить значения корня натуральной степени, степени с рациональным показателем, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
– составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осущест-влять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
– выполнять основные действия со степенями с целыми показателями, с многочленами и алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
– применять свойства арифметических квадратов корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
– решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные уравнения;
– решать линейные и квадратные неравенства с одной переменной и их системы;
– решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
– изображать числа точками на координатной прямой;
– определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
– распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
– находить значения функции, заданной формулой, таблицей, графиком по её аргументу; находить значения аргумента по значению функции, заданной графиком или таблицей;
– определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
– описывать свойства изученных функций, строить их графики;
– извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
– решать комбинаторные задачи путём систематического перебора возможных вариантов и с использованием правила умножения;
– вычислять средние значения результатов измерений;
– находить частоту события, используя собственные наблюдения и готовые статистические данные;
– находить вероятности случайных событий в простейших случаях;
-проводить операции над векторами с данными координатами;
-решать простейшие задачи методом координат;
-составлять уравнения окружности и прямой;
-определять значения тригонометрических функций для углов от 0 до 180;
-применять основное тригонометрическое тождество при решении задач;
-решать треугольники по двум сторонам и углу между ними, по стороне и прилежащим к ней углам, по трем сторонам;
-строить правильные многоугольники с помощью циркуля и линейки;
-решать задачи на применение формул длины окружности и ее дуги, площади круга и кругового сектора;
-выполнять построение движений, осуществлять преобразования фигур.
владеть компетенциями: познавательной, коммуникативной, информационной и рефлексивной;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
–понимания взаимосвязи учебного предмета с особенностями профессий и профессиональной деятельности, в основе которых лежат знания по математике;
–самостоятельного приобретения и применения знаний в различных ситуациях;
–работы в группах;
–аргументирования и отстаивания своей точки зрения;
–извлечения учебной информации на основе сопоставительного анализа объектов;
–самостоятельно действовать в ситуации неопределённости при решении актуальных для них проблем.
Литература и средства обучения
Методические и учебные пособия
А.Г. Мордкович, Н.П. Николаев. Алгебра-9. Ч.1.Учебник. – М.: Мнемозина, 2014
А.Г. Мордкович, Л.И.Звавич, А.Р. Рязановский, Л.А. Александрова. Алгебра-9.Ч.2. Задачник. – М.: Мнемозина,2014
А.Г. Мордкович. Преподавание алгебры в 7-9 классах по учебникам А.Г. Мордковича, Н.П.Николаева. Методическое пособие для учителя. – М.: Мнемозина, 2013
Алгебра. Тесты для промежуточной аттестации. 7-8 класс./ Под ред. Ф.Ф.Лысенко. – Ростов-на-Дону: Легион-М, 2009
Алгебра. 9 класс. Контрольные работы для учащихся общеобразоват. учрежд./ Л.А.Александрова; под ред. А.Г.Мордковича. – М.: Мнемозина, 2010
Алгебра. 9 класс. Самостоятельные работы для учащихся общеобразовательных учреждений/ Л.А.Александрова; под ред. А.Г.Мордковича. – М.: Мнемозина, 2012
Геометрия: Учеб. Для 7-9 кл. общеобразоват. учреждений/Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. – М.: Просвещение, 2010
Зив Б.Г., Мейлер В.М. Дидактические материалы по геометрии для 9 класса. – М.: Просвещение, 2010
Изучение геометрии в 7-9 классах: Метод. рекомендации к учеб.: Кн. для учителя/ Л.С.Атанасян, В.Ф.Бутузов, Ю.А.Глазков и др. – М.: Просвещение, 2009
Мищенко Т.М. Дидактические карточки-задания по геометрии: 9 класс: К учебнику Л.С.Атанасяна и др. «Геометрия 7-9 кл.». – М.: Изд-во «Экзамен», 2011
Мордкович А.Г., Семенов П.В. События. Вероятности. Статистическая обработка данных. 7-9 классы. – М.: Мнемозина, 2009
Научно-теоретический и методический журнал «Математика в школе»
Программы. Математика. 5—6 классы. Алгебра. 7-9 классы. Алгебра и начала математического анализа. 10—11 классы / авт.-сост. И. И. Зубарева, А. Г. Мордкович. – М.: Мнемозина, 2011
Сборник рабочих программ. Геометрия. 7-9 кл.: пособие для учителей общеобразовательных учреждений /Сост. Т.А. Бурмистрова. – М.: Просвещение, 2011
Учебно-методический журнал «Математика. Первое сентября».
Оборудование и приборы
Аудиторная доска с магнитной поверхностью и набором приспособлений для крепления таблиц.
Комплект инструментов классных: линейка, транспортир, угольник (300, 600), угольник (450, 450), циркуль.
ПК (или ноутбук)
Мультимедийный проектор, экран (или интерактивная доска)
Дидактический материал
Карточки для проведения самостоятельных работ по всем темам курса.
Карточки для проведения контрольных работ.
Карточки для индивидуального опроса учащихся по всем темам курса.
Тесты.
Интернет-ресурсы
http://urokimatematiki.ru
http://festival.1september.ru
http://www.uchportal.ru







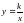 ,
, 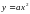 ,
, 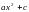 ,
, 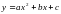 в зависимости от значений коэффициентов;
в зависимости от значений коэффициентов;









