

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Рабочая программа по предмету «Математика: алгебра и начала математического анализа, геометрия» (углублённый уровень) 10-11 классы. ФГОС СОО.
Рабочая программа по математике (алгебра и начала математического анализа и геометрия) 10-11 классов составлена на основе Федерального государственного образовательного стандарта среднего общего образования и является составной частью Основной образовательной программы СОО МБОУ г. Абакана «Лицей».
На изучение предмета математика (алгебра и начала математического анализа, геометрия) в 10-11 классах на углублённом уровне отводится:
|
|
10 класс |
11 класс |
Итого |
|
Математика |
272 |
264 |
536 |
|
Алгебра и начала математического анализа |
170 |
165 |
335 |
|
Геометрия |
102 |
99 |
201 |
Просмотр содержимого документа
«Рабочая программа по предмету «Математика: алгебра и начала математического анализа, геометрия» (углублённый уровень) 10-11 классы. ФГОС СОО.»
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «ЛИЦЕЙ» ГОРОДА АБАКАНА
|
Рассмотрено на заседании ШМО Протокол № 1 от «___» августа 2017 г. № 263 от «01»сентября 2016 г. «29» августа 2016 г.
|
Рассмотрено на заседании Кафедры развивающего обучения Протокол от «____» августа 2017г. № 1
|
Утверждено Приказом по МБОУ «Лицей» г. Абакана № от «____» сентября 2017 г |
Рабочая программа
по предмету «Математика:
алгебра и начала математического анализа, геометрия»
(углублённый уровень)
10-11 классы
2017 год
Пояснительная записка
Рабочая программа по математике (алгебра и начала математического анализа и геометрия) 10-11 классов составлена на основе Федерального государственного образовательного стандарта среднего общего образования и является составной частью Основной образовательной программы СОО МБОУ г. Абакана «Лицей».
В соответствии с принятой Концепцией развития математического образования в Российской Федерации математическое образование решает следующие ключевые задачи:
«предоставлять каждому обучающемуся возможность достижения уровня математических знаний, необходимого для дальнейшей успешной жизни в обществе»;
«обеспечивать необходимое стране число выпускников, математическая подготовка которых достаточна для продолжения образования в различных направлениях и для практической деятельности, включая преподавание математики, математические исследования, работу в сфере информационных технологий и др.»;
«предусмотреть подготовку обучающихся в соответствии с их запросами к уровню подготовки в сфере математического образования».
Соответственно, выделяются три направления требований к результатам математического образования:
практико-ориентированное математическое образование (математика для жизни);
математика для использования в профессии;
творческое направление, на которое нацелены те обучающиеся, которые планируют заниматься творческой и исследовательской работой в области математики, физики, экономики и других областях.
Эти направления реализуются в двух блоках требований к результатам математического образования.
На углубленном уровне:
Выпускник научится в 10–11-м классах: для успешного продолжения образования по специальностям, связанным с прикладным использованием математики.
Выпускник получит возможность научиться в 10–11-м классах: для обеспечения возможности успешного продолжения образования по специальностям, связанным с осуществлением научной и исследовательской деятельности в области математики и смежных наук.
В соответствии с Федеральным законом «Об образовании в РФ» (ст. 12 п. 7) лицей реализует эти требования в образовательном процессе с учетом Основной образовательной программы лицея ![]() как на основе учебно-методических комплектов соответствующего уровня, входящих в Федеральный перечень Министерства образования и науки Российской Федерации, так и с возможным использованием иных источников учебной информации (учебно-методические пособия, образовательные порталы и сайты и др.).
как на основе учебно-методических комплектов соответствующего уровня, входящих в Федеральный перечень Министерства образования и науки Российской Федерации, так и с возможным использованием иных источников учебной информации (учебно-методические пособия, образовательные порталы и сайты и др.).
При изучении математики на углубленном уровне предъявляются требования, соответствующие направлению «математика для профессиональной деятельности»; вместе с тем выпускник получает возможность изучить математику на гораздо более высоком уровне, что создаст фундамент для дальнейшего серьезного изучения математики в вузе.
На изучение предмета математика (алгебра и начала математического анализа, геометрия) в 10-11 классах на углублённом уровне отводится:
|
| 10 класс | 11 класс | Итого |
| Математика | 272 | 264 | 536 |
| Алгебра и начала математического анализа | 170 | 165 | 335 |
| Геометрия | 102 | 99 | 201 |
Планируемые результаты
| Углубленный уровень «Системно-теоретические результаты» | ||
| Раздел | Выпускник научится | Выпускник получит возможность научиться |
| Цели освоения предмета | Для успешного продолжения образования по специальностям, связанным с прикладным использованием математики | Для обеспечения возможности успешного продолжения образования по специальностям, связанным с осуществлением научной и исследовательской деятельности в области математики и смежных наук |
| Элементы теории множеств и математической логики |
В повседневной жизни и при изучении других предметов:
|
В повседневной жизни и при изучении других предметов:
|
| Числа и выражения |
В повседневной жизни и при изучении других предметов:
|
|
| Уравнения и неравенства |
В повседневной жизни и при изучении других предметов:
|
|
| Функции |
интерпретировать свойства в контексте конкретной практической ситуации;
|
|
| Элементы математического анализа |
В повседневной жизни и при изучении других учебных предметов:
|
|
| Статистика и теория вероятностей, логика и комбинаторика
|
В повседневной жизни и при изучении других предметов:
|
|
| Текстовые задачи |
В повседневной жизни и при изучении других предметов:
|
|
| Геометрия |
В повседневной жизни и при изучении других предметов:
|
|
| Векторы и координаты в пространстве |
|
|
| История математики |
|
|
| Методы математики |
|
|
Содержание среднего общего образования по учебному предмету «Математика»
(10-11 классы. Углублённый уровень)
Алгебра и начала математического анализа 335 ч.
Повторение
Решение задач с использованием свойств чисел и систем счисления, делимости, долей и частей, процентов, модулей чисел.
Решение задач с использованием свойств степеней и корней, многочленов, преобразований многочленов и дробно-рациональных выражений.
Решение задач с использованием градусной меры угла.
Модуль числа и его свойства.
Решение задач на движение и совместную работу, смеси и сплавы с помощью линейных, квадратных и дробно-рациональных уравнений и их систем.
Решение задач с помощью числовых неравенств и систем неравенств с одной переменной, с применением изображения числовых промежутков.
Решение задач с использованием числовых функций и их графиков.
Использование свойств и графиков линейных и квадратичных функций, обратной пропорциональности и функции
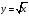 .
. Графическое решение уравнений и неравенств.
Использование операций над множествами и высказываниями.
Использование неравенств и систем неравенств с одной переменной, числовых промежутков, их объединений и пересечений.
Применение при решении задач свойств арифметической и геометрической прогрессии, суммирования бесконечной сходящейся геометрической прогрессии.
Элементы теории множеств и математической логики
Множества (числовые, геометрических фигур). Характеристическое свойство, элемент множества, пустое, конечное, бесконечное множество. Способы задания множеств Подмножество.
Отношения принадлежности, включения, равенства. Операции над множествами. Круги Эйлера. Конечные и бесконечные, счетные и несчетные множества.
Истинные и ложные высказывания, операции над высказываниями. Алгебра высказываний. Связь высказываний с множествами. Кванторы существования и всеобщности.
Законы логики. Основные логические правила. Решение логических задач с использованием кругов Эйлера, основных логических правил.
Умозаключения. Обоснования и доказательство в математике. Теоремы. Виды математических утверждений. Виды доказательств.
Математическая индукция. Утверждения: обратное данному, противоположное, обратное противоположному данному.
Признак и свойство, необходимые и достаточные условия.
Числа и выражения
Основная теорема арифметики. Остатки и сравнения. Алгоритм Евклида. Китайская теорема об остатках. Функция Эйлера, число и сумма делителей натурального числа.
Радианная мера угла, тригонометрическая окружность. Тригонометрические функции чисел и углов. Формулы приведения, сложения тригонометрических функций, формулы двойного и половинного аргумента. Преобразование суммы, разности в произведение тригонометрических функций, и наоборот.
Степень с действительным показателем, свойства степени.
Логарифм, свойства логарифма. Десятичный и натуральный логарифм. Преобразование логарифмических выражений.
Первичные представления о множестве комплексных чисел. Действия с комплексными числами. Комплексно сопряженные числа. Модуль и аргумент числа. Тригонометрическая форма комплексного числа.
Уравнения и неравенства
Тригонометрические уравнения. Однородные тригонометрические уравнения. Решение простейших тригонометрических неравенств. Простейшие системы тригонометрических уравнений.
Простейшие показательные уравнения и неравенства.
Логарифмические уравнения и неравенства.
Иррациональные уравнения.
Решение уравнений в комплексных числах.
Метод интервалов для решения неравенств.
Графические методы решения уравнений и неравенств. Решение уравнений и неравенств, содержащих переменную под знаком модуля.
Системы показательных, логарифмических и иррациональных уравнений. Системы показательных, логарифмических и иррациональных неравенств.
Уравнения, системы уравнений с параметром.
Решение текстовых задач с помощью уравнений, неравенств и их систем.
Формула Бинома Ньютона. Решение уравнений степени выше 2 специальных видов. Теорема Виета, теорема Безу. Приводимые и неприводимые многочлены. Основная теорема алгебры. Симметрические многочлены.
Диофантовы уравнения. Цепные дроби. Теорема Ферма о сумме квадратов.
Неравенство Коши–Буняковского.
Функции
Нули функции, промежутки знакопостоянства, монотонность. Наибольшее и наименьшее значение функции. Периодические функции и наименьший период. Четные и нечетные функции.
Функции «дробная часть числа»
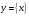 и «целая часть числа»
и «целая часть числа»  .
.Тригонометрические функции числового аргумента
 ,
,  ,
, 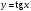 ,
, 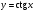 . Свойства и графики тригонометрических функций.
. Свойства и графики тригонометрических функций.Обратные тригонометрические функции, их главные значения, свойства и графики.
Показательная функция и ее свойства и график. Число
 и функция
и функция 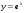 .
. Логарифмическая функция и ее свойства и график.
Степенная функция и ее свойства и график.
Преобразования графиков функций: сдвиг, умножение на число, отражение относительно координатных осей.
Взаимно обратные функции. Графики взаимно обратных функций.
6. Элементы математического анализа
Суммы и ряды, методы суммирования и признаки сходимости.
Понятие предела функции в точке. Понятие предела функции в бесконечности. Асимптоты графика функции. Непрерывность функции. Свойства непрерывных функций. Теорема Вейерштрасса.
Дифференцируемость функции. Производная функции в точке. Касательная к графику функции. Геометрический и физический смысл производной. Применение производной в физике. Производные элементарных функций. Правила дифференцирования.
Вторая производная, ее геометрический и физический смысл.
Точки экстремума (максимума и минимума). Исследование элементарных функций на точки экстремума, наибольшее и наименьшее значение с помощью производной. Построение графиков функций с помощью производных. Применение производной при решении задач.
Первообразная. Неопределенный интеграл. Первообразные элементарных функций. Площадь криволинейной трапеции. Формула Ньютона-Лейбница. Определенный интеграл. Вычисление площадей плоских фигур и объемов тел вращения с помощью интеграла.
Вероятность и статистика, логика, теория графов и комбинаторика
Условная вероятность. Правило умножения вероятностей. Формула полной вероятности. Формула Байеса.
Дискретные случайные величины и распределения. Совместные распределения. Распределение суммы и произведения независимых случайных величин. Математическое ожидание и дисперсия случайной величины. Математическое ожидание и дисперсия суммы случайных величин.
Бинарная случайная величина, распределение Бернулли. Геометрическое распределение. Биномиальное распределение и его свойства.
Непрерывные случайные величины. Плотность вероятности. Функция распределения. Равномерное распределение.
Распределение Пуассона и его применение. Нормальное распределение. Функция Лапласа. Параметры нормального распределения. Примеры случайных величин, подчиненных нормальному закону (погрешность измерений, рост человека).
Неравенство Чебышева. Теорема Чебышева и теорема Бернулли. Закон больших чисел. Выборочный метод измерения вероятностей. Роль закона больших чисел в науке, природе и обществе.
Ковариация двух случайных величин. Понятие о коэффициенте корреляции. Совместные наблюдения двух случайных величин.
Статистическая гипотеза. Статистика критерия и ее уровень значимости. Проверка простейших гипотез.
Принцип Дирихле.
Кодирование. Двоичная запись.
Основные понятия теории графов. Деревья. Двоичное дерево. Связность. Компоненты связности. Пути на графе. Эйлеровы и Гамильтоновы пути.
Геометрия (201 ч)
Повторение
Решение задач с использованием свойств фигур на плоскости.
Решение задач на доказательство и построение контрпримеров.
Применение простейших логических правил.
Решение задач с использованием теорем о треугольниках, соотношений в прямоугольных треугольниках, фактов, связанных с четырехугольниками.
Решение задач с использованием фактов, связанных с окружностями.
Решение задач на измерения на плоскости, вычисления длин и площадей.
Параллельные прямые и плоскости
Основные понятия геометрии в пространстве. Аксиомы стереометрии и следствия из них. Понятие об аксиоматическом методе.
Скрещивающиеся прямые в пространстве. Угол между ними. Методы нахождения расстояний между скрещивающимися прямыми.
Теоремы о параллельности прямых и плоскостей в пространстве. Параллельное проектирование и изображение фигур. Геометрические места точек в пространстве.
Общий перпендикуляр двух скрещивающихся прямых.
Перпендикулярность прямых и плоскостей в пространстве
Перпендикулярность прямой и плоскости. Ортогональное проектирование. Наклонные и проекции. Теорема о трех перпендикулярах.
Углы в пространстве. Перпендикулярные плоскости. Площадь ортогональной проекции. Перпендикулярное сечение призмы. Трехгранный и многогранный угол. Свойства плоских углов многогранного угла.
Геометрические преобразования пространства
Подобие в пространстве. Отношение объемов и площадей поверхностей подобных фигур.
Движения в пространстве: параллельный перенос, симметрия относительно плоскости, центральная симметрия, поворот относительно прямой.
Преобразование подобия, гомотетия. Решение задач на плоскости с использованием стереометрических методов.
Многогранники
Призма, параллелепипед, пирамида, тетраэдр.
Теорема Менелая для тетраэдра. Построение сечений многогранников методом следов. Центральное проектирование. Построение сечений многогранников методом проекций.
Виды тетраэдров. Ортоцентрический тетраэдр, каркасный тетраэдр, равногранный тетраэдр. Прямоугольный тетраэдр. Достраивание тетраэдра до параллелепипеда.
Виды многогранников. Развертки многогранника.
Теорема Эйлера. Правильные многогранники.
Призма. Параллелепипед. Свойства параллелепипеда. Прямоугольный параллелепипед. Наклонные призмы.
Пирамида. Виды пирамид. Элементы правильной пирамиды. Пирамиды с равнонаклоненными ребрами и гранями, их основные свойства.
Площади поверхностей многогранников.
Поверхности и тела вращения
Тела вращения: цилиндр, конус, шар и сфера. Сечения цилиндра, конуса и шара. Шаровой сегмент, шаровой слой, шаровой сектор (конус).
Усеченная пирамида и усеченный конус.
Элементы сферической геометрии. Конические сечения.
Касательные прямые и плоскости. Вписанные и описанные сферы. Касающиеся сферы. Комбинации тел вращения.
Площадь сферы.
Развертка цилиндра и конуса. Площадь поверхности цилиндра и конуса.
Комбинации многогранников и тел вращения.
Объемы геометрических тел
Понятие объема.
Объемы многогранников.
Объемы тел вращения.
Аксиомы объема. Вывод формул объемов прямоугольного параллелепипеда, призмы и пирамиды. Формулы для нахождения объема тетраэдра.
Приложения интеграла к вычислению объемов и поверхностей тел вращения.
Площадь сферического пояса. Объем шарового слоя.
Применение объемов при решении задач.
Векторы и координаты в пространстве
Векторы и координаты. Сумма векторов, умножение вектора на число. Угол между векторами. Скалярное произведение.
Уравнение плоскости. Формула расстояния между точками. Уравнение сферы. Формула расстояния от точки до плоскости. Способы задания прямой уравнениями.
Тематическое планирование
|
| Содержание | Количество часов | Характеристика основных видов деятельности ученика |
|
| Алгебра и начала математического анализа (10 класс) 170 часов | ||
|
| Повторение ключевых тем алгебры 7-9 классов (10 ч) | ||
| | Решение задач с использованием свойств чисел и систем счисления, делимости, долей и частей, процентов, модулей чисел. | 1 |
|
| | Решение задач с использованием свойств степеней и корней, многочленов, преобразований многочленов и дробно-рациональных выражений. | 1 | |
| | Решение задач с использованием градусной меры угла. Модуль числа и его свойства. | 1 | |
| | Решение задач на движение и совместную работу, смеси и сплавы с помощью линейных, квадратных и дробно-рациональных уравнений и их систем. | 1 | |
| | Решение задач с помощью числовых неравенств и систем неравенств с одной переменной, с применением изображения числовых промежутков. Решение задач с использованием числовых функций и их графиков. | 1 | |
| | Использование свойств и графиков линейных и квадратичных функций, обратной пропорциональности и функции | 1 | |
| | Графическое решение уравнений и неравенств. | 1 | |
| | Использование неравенств и систем неравенств с одной переменной, числовых промежутков, их объединений и пересечений. | 1 | |
| | Применение при решении задач свойств арифметической и геометрической прогрессии, суммирования бесконечной сходящейся геометрической прогрессии. | 1 | |
| | Стартовая контрольная работа | 1 | |
|
| Повторение и расширение сведений о множествах, математической логике и функциях (21 ч) | ||
| | Множества, операции над множествами | 2 | Описывать понятия: множества, функции истинности, тавтологии, предиката, области определения предиката, области истинности предиката, кванторов общности и существования. Формулировать определения: подмножества данного множества, собственного подмножества данного множества, пересечения множеств, объединения множеств, разности множеств, взаимнооднозначного соответствия между множествами, равномощных множеств, счетного множества, конъюнкции высказываний, дизъюнкции высказываний, импликации высказываний, эквивалентности высказываний, отрицания высказывания, эквивалентных высказываний, равносильных предикатов, конъюнкции предикатов, дизъюнкции предикатов, импликации предикатов, эквивалентности предикатов, отрицания предиката, взаимообратных теорем, теоремы, противоположной данной, функции, наибольшего и наименьшего значения функции на множестве, четной функции, нечетной функции, обратимой функции, взаимообратных функций. Описывать алгоритмы: построения графиков функций y = f (kx), y = f (|x|), y = | f (x)|, решения неравенств методом интервалов. Доказывать формулы: включения исключения. Формулировать и доказывать теоремы: о графике четной функции, о графике нечетной функции, об обратимости возрастающей (убывающей) функции, о графиках взаимообратных функций, об общих точках графиков возрастающих взаимно-обратных функций и её следствие. Применять изученные определения, теоремы и формулы к решению задач |
| | Конечные и бесконечные множества | 2 | |
| | Высказывания и операции над ними | 2 | |
| | Предикаты. Операции над предикатами. Виды теорем | 2 | |
| | Контрольная работа № 1 | 1 | |
| | Функция и её свойства | 3 | |
| | Построение графиков функций с помощью геометрических преобразований | 2 | |
| | Обратная функция | 2 | |
| | Метод интервалов | 4 | |
| | Контрольная работа № 2 | 1 | |
|
| Степенная функция (26 ч) | ||
| | Степенная функция с натуральным показателем | 1 | Описывать понятия: степенная функция с натуральным показателем, степенная функция с целым показателем, функция корень n-й степени, степенной функции с рациональным показателем. Формулировать определения: корня n-й степени, арифметического корня n-й степени, степени с рациональным показателем, равносильных уравнений, уравнения следствия, равносильных неравенств, неравенства следствия. Доказывать свойства: степенной функции с натуральным показателем, степенной функции с целым показателем, функции корень n-й степени, степенной функции с рациональным показателем. Формулировать и доказывать теоремы: о свойствах корня n-й степени, о свойствах степени с рациональным показателем, о равносильных преобразованиях иррациональных уравнений, о равносильных преобразованиях иррациональных неравенств. Применять изученные определения, теоремы и формулы к решению задач |
| | Степенная функция с целым показателем | 1 | |
| | Определение корня n-й степени. Функция y = xn | 4 | |
| | Свойства корня n-й степени | 4 | |
| | Контрольная работа №3 | 1 | |
| | Степень с рациональным показателем и её свойства | 2 | |
| | Иррациональные уравнения | 4 | |
| | Различный приёмы решения иррациональных уравнений и их систем | 4 | |
| | Иррациональные неравенства | 4 | |
| | Контрольная работа №4 | 1 | |
|
| Тригонометрические функции (32 ч) | ||
| | Радианное измерение углов | 2 | Описывать понятия: тригонометрические функции угла поворота. Формулировать определения: угла в 1 радиан, косинуса, синуса, тангенса и котангенса угла поворота, периодической функции, соизмеримых чисел, ограниченной функции. Доказывать формулы: длины дуги окружности, основные соотношения между тригонометрическими функциями одного и того же аргумента, сложения, приведения, двойного, тройного и половинного углов, понижения степени, для преобразований суммы, разности и произведения тригонометрических функций. Доказывать свойства: тригонометрических функций. Формулировать и доказывать теоремы: о свойствах периодических функций. Применять изученные определения, теоремы и формулы к решению задач, о свойстве функций, имеющих соизмеримые периоды |
| | Радианное измерение углов | 2 | |
| | Знаки значений тригонометрических функций. Чётность и нечётность тригонометрических функций | 2 | |
| | Периодические функции | 2 | |
| | Свойства и графики функций y = sin x и y = cos x | 2 | |
| | Свойства и графики функций y = tg x и y = ctg x | 2 | |
| | Контрольная работа №5 | 1 | |
| | Основные соотношения между тригонометрическими функциями одного и того же аргумента | 4 | |
| | Формулы сложения | 3 | |
| | Формулы приведения | 2 | |
| | Формулы двойного, тройного и половинного углов | 5 | |
| | Формулы для преобразования суммы, разности и произведения тригонометрических функций | 4 | |
| | Контрольная работа №6 | 1 | |
|
| Тригонометрические уравнения и неравенства (31 ч) | ||
| | Уравнение cos x = b | 4 | Описывать понятия: функции y = arccos x, y = arcsin x, y = arctg x и y = arcctg x, простейшего тригонометрического неравенства. Формулировать определения: арккосинуса, арксинуса, арктангенса, арккотангенса, однородных тригонометрических уравнений. Доказывать формулы: корней простейших тригонометрических уравнений. Доказывать свойства: обратных тригонометрических функций. Применять изученные определения, теоремы и формулы к решению задач |
| | Уравнение sin x = b | 4 | |
| | Уравнения tg x = b и ctg x = b | 2 | |
| | Функции y = arccos x, y = x, y = arctg x и y = arcctg x | 5 | |
| | Тригонометрические уравнения, сводящиеся к алгебраическим | 5 | |
| | Решение тригонометрических уравнений методом разложения на множители. Применение ограниченности тригонометрических функций | 5 | |
| | О равносильных переходах при решении тригонометрических уравнений | 2 |
|
| | Тригонометрические неравенства | 4 |
|
| | Контрольная работа №7 | 1 |
|
|
| Производная и её применение (42 ч) | ||
| | Определение предела функции в точке и функции непрерывной в точке | 3 | Описывать понятия: мгновенной скорости, касательной к графику функции, приращения функции в точке, геометрический и механический смысл производной, наибольшего (наименьшего) значения функции на отрезке, второй производной, выпуклой вверх (вниз) функции, асимптоты графика. Формулировать определения: предела функции в точке, функции непрерывной в точке, производной функции в точке, окрестности точки, точки максимума, точки минимума, критической точки функции. Описывать алгоритмы: поиска наибольшего и наименьшего значений функции на отрезке, исследования свойств и построения графика функции. Записывать формулы: производная степенной функции, производная корня n-й степени, производные тригонометрических функций, уравнения касательной к графику функции. Формулировать и доказывать теоремы: о непрерывности дифференцируемой функции, о правилах вычисления производной, о признаке постоянства функции, о признаке возрастания (убывания) функции, о признаке точки максимума (минимума), о признак выпуклой вверх (вниз) функции. Формулирует и поясняет геометрический и механический смыслы теорем: Ферма, Ролля, Лагранжа. Применять изученные определения, теоремы и формулы к решению задач |
| | Задачи о мгновенной скорости и касательной к графику функции | 1 | |
| | Понятие производной | 4 | |
| | Правила вычисления производной | 5 | |
| | Уравнение касательной | 5 | |
| | Контрольная работа №8 | 1 | |
| | Признаки возрастания и убывания функции | 5 | |
| | Точки экстремума функции | 5 | |
| | Наибольшее и наименьшее значения функции на отрезке | 5 | |
| | Вторая производная. Понятие выпуклости функции | 3 | |
| | Построение графиков функций | 4 | |
| | Контрольная работа №9 |
| |
|
| Повторение курса алгебры и начал математического анализа 10 класса | ||
| | Повторение ключевых тем курса 10 класса | 7 |
|
| | Итоговая контрольная работа | 1 | |
|
| Алгебра и начала математического анализа (11 класс) 165 часов | ||
|
| Повторение ключевых тем 10 класса (9 ч) | ||
| | Степенная функция | 2 |
|
| | Тригонометрические функции | 2 | |
| | Тригонометрические уравнения и неравенства | 2 | |
| | Производная и её применение | 2 | |
| | Стартовая контрольная работа | 1 | |
|
| Показательная и логарифмическая функции (34 ч) | ||
| | Степень с произвольным действительным показателем. Показательная функция | 5 | Формулировать определение показательной функции. Описывать свойства показательной функции, выделяя случай основания, большего единицы, и случай положительного основания, меньшего единицы. Преобразовывать выражения, содержащие степени с действительным показателем. Строить графики функций на основе графика показательной функции. Распознавать показательные уравнения и неравенства. Формулировать теоремы о равносильном преобразовании показательных уравнений и неравенств. Решать показательные уравнения и неравенства. Формулировать определение логарифма положительного числа по положительному основанию, отличному от единицы, теоремы о свойствах логарифма. Преобразовывать выражения, содержащие логарифмы. Формулировать определение логарифмической функции и описывать её свойства, выделяя случай основания, большего единицы, и случай положительного основания, меньшего единицы. Доказывать, что показательная и логарифмическая функции являются взаимно обратными. Строить графики функций на основе логарифмической функции. Распознавать логарифмические уравнения и неравенства. Формулировать теоремы о равносильном преобразовании логарифмических уравнений и неравенств. Решать логарифмические уравнения и неравенства. Формулировать определения числа е, натурального логарифма. Находить производные функций, содержащих показательную функцию, логарифмическую функцию, степенную функцию с действительным показателем |
| | Показательные уравнения | 5 | |
| | Показательные неравенства | 5 | |
| | Контрольная работа №1 | 1 | |
| | Логарифм и его свойства | 6 | |
| | Логарифмическая функция и её свойства | 6 | |
| | Логарифмические уравнения | 5 | |
| | Логарифмические неравенства | 7 | |
| | Производные показательной и логарифмической функций | 4 | |
| | Контрольная работа №2 | 1 | |
|
| Интеграл и его применение (18 ч) | ||
| | Первообразная | 4 | Формулировать определение первообразной функции, теорему об основном свойстве первообразной, правила нахождения первообразной. На основе таблицы первообразных и правил нахождения первообразных находить первообразную, общий вид первообразных, неопределенный интеграл. По закону изменения скорости движения материальной точки находить закон движения материальной точки. Формулировать теорему о связи первообразной и площади криволинейной трапеции. Формулировать определение определенного интеграла. Используя формулу Ньютона-Лейбница, находить определенный интеграл, площади фигур, ограниченных данными линиями. Использовать определенный интеграл для нахождения объёмов тел, в частности объёмов тел вращения. |
| | Правила нахождения первообразной | 4 | |
| | Площадь криволинейной трапеции. Определённый интеграл | 7 | |
| | Вычисление объёмов тел | 2 | |
| | Контрольная работа №3 | 1 | |
|
| Элементы комбинаторики. Бином Ньютона (17 ч) | ||
| | Метод математической индукции | 5 | Формулировать последовательность действий при использовании доказательства методом математической индукции. Использовать метод математической индукции для: доказательства неравенств, нахождения конечных сумм, при решении задач по теории чисел. Формулировать определение перестановки конечного множества. Формулировать определение размещения n-элементного множества по k элементов. Формулировать определение сочетания n-элементного множества по k элементов. Использовать формулы: количества перестановок конечного множества, размещений n-элементного множества по k элементов и сочетаний n-элементного множества по k элементов решать задачи комбинаторного характера. Записывать формулу бинома Ньютона. Формулировать свойства треугольника Паскаля и биномиальных коэффициентов. |
| | Метод математической индукции | 4 | |
| | Сочетания (комбинации) | 3 | |
| | Бином Ньютона | 4 | |
| | Контрольная работа №4 | 1 | |
|
| Элементы теории вероятностей (34 ч) | ||
| | Элементы комбинаторики и бином Ньютона | 6 | Формулировать определения несовместных событий, объединения и пересечения событий, дополнения события. Используя формулу вероятности объединения двух несовместных событий, формулу, связывающую вероятности объединения и пересечения двух событий, формулу вероятности дополнения события, находить вероятности событий. Формулировать определения зависимых и независимых событий, условной вероятности. Используя теоремы о вероятности пересечения двух зависимых и независимых событий, теорему о вероятности пересечения нескольких независимых событий, находить вероятности событий. Распознавать вероятностные эксперименты, описываемые с помощью схемы Бернулли. Находить вероятность события, состоящего в том, что в схеме Бернулли успехом завершиться данное количество испытаний. Формулировать определения случайной величины и её множества значений. Для случайной величины с конечным множеством значений формулировать определения распределения случайной величины и её математического ожидания. Находить математическое ожидание случайной величины по её распределению. Использовать выводы теории вероятностей в задачах с практическим жизненным содержанием |
| | Аксиомы теории вероятностей | 4 | |
| | Условная вероятность | 4 | |
| | Независимые события | 3 | |
| | Случайная величина | 4 | |
| | Схема Бернулли. Биномиальное распределение | 4 | |
| | Характеристики случайной величины | 4 | |
| | Математическое ожидание суммы случайных величин | 4 | |
| | Контрольная работа №5 | 1 | |
|
| Итоговое повторение ключевых тем (53 ч) | ||
| | Повторение ключевых тем 11 класса | 8 |
|
| | Повторение ключевых тем алгебры и начал математического анализа 7-11 класса | 43 |
|
| | Итоговая работа в формате ЕГЭ | 2 |
|
Итого контрольных работ по алгебре и началам математического анализа в 10 классе – 11, из них 1 – стартовая, 1 – итоговая; в 11 классе – 7, из них 1 – стартовая, 1 – итоговая.
|
| Содержание | Количество часов | Характеристика основных видов деятельности ученика |
|
| Геометрия (10 класс) 102 часа | ||
|
| Повторение ключевых тем геометрии 7-9 классов (5 ч) | ||
| | Решение задач с использованием теорем о треугольниках, соотношений в прямоугольных треугольниках, фактов, связанных с четырехугольниками. | 1 |
|
| | Решение задач с использованием фактов, связанных с окружностями. | 1 | |
| | Решение задач на измерения на плоскости, вычисление длин и площадей. | 1 | |
| | Решение задач с помощью векторов и координат.
| 1 | |
| | Стартовая контрольная работа | 1 | |
|
| Введение в стереометрию (10 ч). | ||
| | Основные понятия стереометрии. Аксиомы стереометрии | 2 | Перечислять основные понятия стереометрии. Описывать основные понятия стереометрии (точка, прямая, плоскость). Описывать возможные способы расположения точек, прямых и плоскостей в пространстве. Формулировать аксиомы стереометрии. Разъяснять и иллюстрировать аксиомы. Формулировать и доказывать теоремы — следствия из аксиом. Формулировать способы задания плоскости в пространстве. Перечислять и описывать основные элементы многогранников: ребра, вершины, грани. Описывать виды многогранников (пирамида, тетраэдр, призма, прямоугольный параллелепипед, куб), а также их элементы (основания, боковые грани, рёбра основания, боковые ребра). Решать задачи на построение сечений многогранников. |
| | Следствия из аксиом стереометрии | 3 | |
| | Пространственные фигуры. Начальные представления о многогранниках | 4 | |
| | Контрольная работа №1 | 1 | |
|
| Параллельность в пространстве (17 ч) | ||
| | Взаимное расположение двух прямых в пространстве | 3 | Описывать возможные способы расположения в пространстве: двух прямых, прямой и плоскости, двух плоскостей. Формулировать определения: параллельных прямых, скрещивающихся прямых, параллельных прямой и плоскости, параллельных плоскостей, преобразование движения, фигуры симметричной относительно точки, равных фигур, преобразования подобия. Формулировать и доказывать признаки: параллельности двух прямых, параллельности прямой и плоскости, параллельности двух плоскостей, скрещивающихся прямых. Формулировать и доказывать свойства: параллельных прямых, параллельных плоскостей. Формулировать и доказывать теоремы: о существовании и единственности плоскости, проходящей через две параллельные прямые, о существовании и единственности прямой, проходящей через данную точку и параллельной данной прямой, о существовании и единственности плоскости, проходящий через точку и параллельной данной плоскости, о свойствах параллельного проектирования. Формулировать теорему Польке-Шварца. Решать задачи на построение сечений многогранников, а также построение изображений фигур. |
| | Параллельность прямой и плоскости | 4 | |
| | Параллельность плоскостей | 4 | |
| | Преобразование фигур в пространстве. Параллельное проектирование | 2 | |
| | Изображение плоских и пространственных фигур | 3 | |
| | Контрольная работа №2 | 1 | |
|
| Перпендикулярность в пространстве (42 ч) | ||
| | Угол между прямыми в пространстве | 3 | Формулировать определения: угла между пересекающимися прямыми, угла между скрещивающимися прямыми, прямой перпендикулярной плоскости, угла между прямой и плоскостью, угла между двумя плоскостями, величины двугранного угла, перпендикулярных плоскостей, точек симметричных относительно плоскости, фигур симметричных относительно плоскости, расстояния от точки до плоскости, расстояния от прямой до параллельной ей плоскости, расстояние между параллельными плоскостями, общего перпендикуляра двух скрещивающихся прямых, выпуклого многогранного угла, геометрического места точек пространства, биссектор двухгранного угла. Описывать понятия: перпендикуляр, наклонная, основание перпендикуляра, основание наклонной, проекция наклонной, ортогональная проекция фигуры, расстояние между скрещивающимися прямыми, зеркальная симметрия, двугранный угол, грань двугранного угла, ребро двугранного угла, линейный угол двугранного угла, многогранный угол, вершина многогранного угла, ребро многогранного угла, грань многогранного угла, двугранный угол многогранного угла. Формулировать и доказывать признаки: перпендикулярности прямой и плоскости, перпендикулярности двух плоскостей. Формулировать и доказывать свойства: перпендикулярных прямых, прямых перпендикулярных плоскости, перпендикулярных плоскостей. Формулировать и доказывать теоремы: об угле между пересекающимися прямыми, о существовании и единственности прямой, проходящий через данную точку и перпендикулярной данной плоскости, о параллельности плоскостей, перпендикулярных данной прямой, о перпендикуляре и наклонной, проведенных из одной точки, о трех перпендикулярах, о площади ортогональной проекции выпуклого многоугольника, косинусов и синусов для трехгранного угла, о свойствах плоских углов трехгранного угла, ГМТ равноудаленных от концов отрезка, ГМТ принадлежащих двугранному углу и равноудаленных от его граней. Решать задачи на доказательство, а также вычисление: угла между прямыми, угла между прямой и плоскостью, угла между плоскостями, расстояния от точки до прямой, расстояния от точки до плоскости, расстояния между скрещивающимися прямыми, расстояния между параллельными плоскостями, площади ортогональной проекции выпуклого многоугольника |
| | Перпендикулярность прямой и плоскости | 5 | |
| |
| 5 | |
| |
| 5 | |
| | Контрольная работа №3 | 1 | |
| | Угол между прямой и плоскостью | 4 | |
| | Двугранный угол. Угол между двумя плоскостями | 5 | |
| | Перпендикулярные плоскости | 5 | |
| | Площадь ортогональной проекции многоугольника | 3 | |
| | Многогранный угол. Трехгранный угол | 3 | |
| | Геометрическое место точек пространства | 2 | |
| | Контрольная работа №4 | 1 | |
| | |
| |
| | Многогранники (22 ч) | ||
| | Призма | 5 | Формулировать определения: многогранника, выпуклого многогранника, призмы, прямой призмы, правильной призмы, параллелепипеда, пирамиды, правильной пирамиды, правильного тетраэдра, высоты призмы, высоты пирамиды, высоты усеченной пирамиды, апофемы правильной пирамиды и правильной усеченной пирамиды, ортоцентрического тетраэдра, средней линии тетраэдра, медианы тетраэдра, равногранного тетраэдра. Формулировать теорему Эйлера. Формулировать и доказывать теоремы: о площади боковой поверхности прямой призмы, о диагоналях параллелепипеда, о квадрате диагонали прямоугольного параллелепипеда, о площади боковой поверхности правильной пирамиды, о площади боковой поверхности правильной усеченной пирамиды, о признаке ортоцентрического тетраэдра, о средних линиях тетраэдра, о медианах тетраэдра, Менелая для тетраэдра. Решать задачи на доказательство, а также вычисление: элементов призмы и пирамиды, площади полной и боковой поверхности призмы и пирамиды. |
| | Параллелепипед | 4 | |
| | Пирамида | 6 | |
| | Усеченная пирамида | 2 | |
| | Тетраэдр | 4 | |
| | Контрольная работа №5 | 1 | |
| | Повторение ключевых тем 10 класса (6 ч) | ||
| | Повторение ключевых тем 10 класса | 4 | |
| | Итоговая контрольная работа | 2 | |
| | Геометрия (11 класс) 99 часов | ||
| | Повторение ключевых тем 10 класса (5 ч) | ||
| | Параллельность в пространстве | 2 | |
| | Перпендикулярность в пространстве | 2 | |
| | Стартовая контрольная работа | 1 | |
| | Координаты и векторы в пространстве (23 ч) | ||
| | Декартовы координаты точки в пространстве | 3 | Описывать понятия: прямоугольная система координат в пространстве, координаты точки, вектор, сонаправленные и противоположно направленные векторы, параллельный перенос на вектор, сумма векторов, базис, координаты вектора в базисе, гомотетия с коэффициентом равным k, угол между векторами. Формулировать определения: коллинеарных векторов, равных векторов, компланарных векторов, разности векторов, противоположных векторов, произведения вектора и числа, скалярное произведение двух векторов, уравнение фигуры. Формулировать свойства: суммы векторов, умножения вектора на число, гомотетии, скалярного произведения. Доказывать формулы: расстояния между двумя точками (с заданными координатами), координат середины отрезка, координат точки, делящей отрезок в данном отношении, координат суммы и разности векторов, скалярного произведения двух векторов, для вычисления косинуса угла между двумя ненулевыми векторами, расстояния от точки до плоскости. Формулировать и доказывать теоремы: о координатах вектора (при заданных координатах его начала и конца), о коллинеарных векторах, о компланарных векторах, о разложении вектора по трем некомпланарным векторам, о скалярном произведении двух перпендикулярных векторов, об уравнении плоскости, о векторе перпендикулярном данной плоскости. Применять изученные определения, теоремы и формулы к решению задач |
| | Векторы в пространстве | 2 | |
| | Сложение и вычитание векторов | 3 | |
| | Умножение вектора на число. Гомотетия | 5 | |
| | Скалярное произведение векторов | 5 | |
| | Уравнение плоскости | 4 | |
| | Контрольная работа №1 | 1 | |
| | Тела вращения (37 ч) | ||
| | Цилиндр | 3 | Описывать понятия: цилиндр, боковая поверхность цилиндра, образующая цилиндра, поворот фигуры вокруг прямой на данный угол, тело вращения, осевое сечение цилиндра, развертка цилиндра, касательная плоскость к цилиндру, боковая поверхность конуса, осевое сечение конуса, развертка конуса, усеченный конус, усеченная пирамида, описанная вокруг усеченного конуса, усеченная пирамида, вписанная в усеченный конус, фигура касается сферы, сфер, касающихся внешним образом и внутренним образом. Формулировать определения: призмы, вписанной в цилиндр, призмы, описанной около цилиндра, пирамиды, вписанной в конус, пирамиды, описанной около конуса, сферы и шара, а также их элементов, касательной плоскости к сфере, многогранника, вписанного в сферу, многогранника, описанного около сферы, цилиндра, вписанного в сферу, конуса, вписанного в сферу, усеченного конуса, вписанного в сферу, цилиндра, описанного около сферы, конуса, описанного около сферы, усеченного конуса, описанного около сферы. Доказывать формулы: площади боковой поверхности цилиндра, площади полной поверхности цилиндра, площади боковой поверхности конуса, площади боковой поверхности усеченного конуса. Формулировать и доказывать теоремы: об уравнении сферы данного радиуса с центром в данной точке, о касательной плоскости к сфере и следствие, о прямой, касательной к сфере, о существовании сферы, описанной около цилиндра, о существовании сферы, описанной около конуса, о существовании сферы, описанной около усеченного конуса, о цилиндре, описанном около сферы, о существовании сферы, вписанной в конус, об усеченном конусе, описанном около сферы. Применять изученные определения, теоремы и формулы к решению задач |
| | Комбинации цилиндра и призмы | 3 | |
| | Конус | 3 | |
| | Усеченный конус | 2 | |
| | Комбинации конуса и пирамиды | 4 | |
| | Контрольная работа №2 | 1 | |
| | Сфера и шар. Уравнение сферы |
| |
| | Взаимное расположение сферы и плоскости | 4 | |
| | Многогранники, вписанные в сферу | 7 | |
| | Многогранники, описанные около сферы | 2 | |
| | Тела вращения, вписанные в сферу | 5 | |
| | Тела вращения, описанные около сферы | 4 | |
| | Контрольная работа №3 | 1 | |
| | Объёмы тел. Площадь сферы (19 ч) | ||
| | Объем тела. Формулы для вычисления объёма призмы | 4 | Описывать понятия: шаровой слой, шаровой сектор. Формулировать определения: объем тела, площади поверхности шара. Доказывать формулы: объема призмы, объема пирамиды, объема усеченной пирамиды, объема конуса, объема усеченного конуса, объема цилиндра, объема шара, объёма тела вращения, объема шарового сектора, слоя и сегмента, площади сферы, площади сферической части поверхности шарового сегмента. Применять изученные определения, теоремы и формулы к решению задач |
| | Формулы для вычисления объёмов пирамиды и усеченной пирамиды | 6 | |
| | Контрольная работа №4 | 1 | |
| | Объемы тел вращения | 5 | |
| | Площадь сферы | 2 | |
| | Контрольная работа №5 | 1 | |
| | Повторение ключевых те геометрии 7- 11 классов (15 ч) | ||
| | Повторение ключевых тем геометрии 7--11 | 13 | |
| | Итоговая контрольная работа в формате ЕГЭ | 2 | |
Итого контрольных работ геометрии в 10 классе – 7, из них 1 – стартовая, 1 – итоговая; в 11 классе – 7, из них 1 – стартовая, 1 – итоговая.














