МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
Г. ИРКУТСКА
| РАССМОТРЕНО на заседании МО протокол № _____ от ___ ___________2020 г.
|
| УТВЕРЖДАЮ директор МБОУ г.Иркутска СОШ № 42 ________Н.В. Зарипова №01-06-98-1/21 от 31.08.2021___ ___________2020 г.
|
СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 42
РАБОЧАЯ ПРОГРАММА
ПО ПРЕДМЕТУ «АЛГЕБРА И НАЧАЛА
МАТЕМАТИЧЕСКОГО АНАЛИЗА»
ДЛЯ 11 КЛАССА
НА 2021-2022 УЧ.Г.
Составитель:
Барташкина О.В.,
учитель математики,
первая квалификационная категория
2021г.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Рабочая программа по алгебре и началам математического анализа составлена на основе Федерального компонента государственного образовательного стандарта общего образования, утверждённого приказом Министерства образования РФ от 05. 03. 2004 г. № 1089.
Нормативную основу рабочей программы составили:
Учебный план МБОУ г. Иркутска СОШ № 42 на 2021-2022 учебный год;
Примерные программы:
- Алгебра и начала математического анализа. Сборник рабочих программ. 10-11 классы: учеб. пособие для учителей общеобразоват. организаций: базовый и углубл. уровни / [сост. Т. А. Бурмистрова]. – 2-е изд., перераб. - М.: Просвещение, 2018.
Роль математики в развитии общества в целом и формировании личности каждого отдельного человека определяет цели и задачи обучения математике в общеобразовательной школе:
овладение конкретными математическими знаниями, необходимыми для применения в конкретной практической деятельности, для изучения смежных дисциплин, доля продолжения образования;
интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых для продуктивной жизни в обществе;
формирование представлений об идеях и методах математики, о математике как форме описания и методе познания действительности;
формирование представлений о математике как части общечеловеческой культуры, понимания значимости математики для общечеловеческого прогресса.
Цель изучения курса алгебры и начал математического анализа в 10-11 классах - систематическое изучение функции, как важнейшего математического объекта средствами алгебры и математического анализа, раскрытие политехнического и прикладного значения общих методов математики, связанных с исследованием функций, подготовка необходимого аппарата для изучения геометрии и физики.
Рабочая программа ориентирована на усвоение обязательного минимума математического образования, позволяет работать без перегрузок в классе с детьми разного уровня обучения и интереса к математике.
В процессе реализации рабочей программы решаются не только задачи общего математического образования, но и дополнительные, направленные на:
использование личностных особенностей учащихся в процессе обучения;
формирование у учащихся математического стиля мышления.
ОБЩАЯ ХАРАКТЕРИСТИКА УЧЕБНОГО ПРЕДМЕТА
Содержание по алгебре и началам математического анализа включает следующие разделы: «Алгебра», «Математический анализ», «Вероятность и статистика».
Содержание раздел «Алгебра» способствует формированию у учащихся математического аппарата для решения задач окружающей реальности. Продолжается изучение многочленов с целыми коэффициентами, методов нахождения их рациональных корней. Происходит развитие и завершение базовых знаний о числе. Основное назначение этих вопросов связно с повышением общей математической подготовки учащихся, освоением простых и эффективных приемов решения алгебраических задач.
Раздел «Математический анализ» представлен тремя основными темами: «Элементарные функции», «Производная» и «Интеграл». Содержание этого раздела нацелено на получение школьниками конкретных знаний о функции как важнейшей модели описания и исследования разнообразных реальных процессов. Изучение степенных, показательных, логарифмических и тригонометрических функций продолжает знакомство учащихся с основными элементарными функциями, начатое в основной школе. Помимо овладения непосредственными умениями решать соответствующие уравнения и неравенства, у учащихся формируется запас геометрических представлений, лежащих в основе объяснения правомерности стандартных и эвристических приемов решения задач. Темы «Производная» и «Интеграл» содержат традиционно трудные вопросы для школьников, поэтому их изложение предполагает опору на геометрическую наглядность и на естественную интуицию учащихся, более, чем на строгие определения. Тем не менее, знакомство с этим материалом дает представление учащимся об общих идеях и методах математической науки. При изучении раздела «Вероятность и статистика» рассматриваются различные математические модели, позволяющие измерять и сравнивать вероятности различных событий, делать выводы и прогнозы. Этот материал необходим прежде всего для формирования у учащихся функциональной грамотности – умения воспринимать и критически анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей.
МЕСТО ПРЕДМЕТА В УЧЕБНОМ ПЛАНЕ
Согласно учебному плану МБОУ г. Иркутска СОШ № 42 и календарному учебному графику на 2020–2021 учебный год на изучение предмета «Алгебра и начала математического анализа» в 11 классе отводится 3 учебных часа в неделю в течение 34 недель, итого 102 часа в год.
Данное планирование определяет достаточный объем учебного времени для повышения математических знаний учащихся в среднем звене школы, улучшения усвоения других учебных предметов.
ЦЕННОСТНЫЕ ОРИЕНТИРЫ СОДЕРЖАНИЯ УЧЕБНОГО ПРЕДМЕТА
Математическое образование играет важную роль и в практической, и в духовной жизни общества. Практическая сторона связана с созданием и применением инструментария, необходимого человеку в его продуктивной деятельности, духовная сторона – с интеллектуальным развитием человека, формированием характера и общей культуры.
Без конкретных знаний по алгебре и началам математического анализа затруднено понимание принципов устройства и использования современной техники, восприятие и интерпретация разнообразной социальной, экономической, политической информации, малоэффективна повседневная практическая деятельность. Каждому человеку в своей жизни приходится выполнять расчеты, читать информацию, представленную в виде таблиц, диаграмм, графиков, понимать вероятностный характер случайных событий, составлять несложные алгоритмы и др.
Изучение данного курса завершает формирование ценностно-смысловых установок и ориентаций учащихся в отношении математических знаний и проблем их использования в рамках среднего общего образования. Курс способствует формированию умения видеть и понимать их значимость для каждого человека независимо от его профессиональной деятельности; умения различать факты и оценки, сравнивать оценочные выводы, видеть их связь с критериями и связь критериев с определенной системой ценностей.
Без базовой математической подготовки невозможна постановка образования современного человека. В школе математика служит опорным предметом для изучения смежных дисциплин. Реальной необходимостью в наши дни становится непрерывное образование, что требует полноценной базовой общеобразовательной подготовки, в том числе и по алгебре и началам математического анализа.
Для жизни в современном обществе важным является формирование математического стиля мышления. Объекты математических умозаключений и правила их конструирования вскрывают механизм логических построений, вырабатывают умения формулировать, обосновывать и доказывать суждения, тем самым развивают логическое мышление. Алгебре и началам математического анализа принадлежит ведущая роль в формировании алгоритмического мышления, воспитании умений действовать по заданному алгоритму. В ходе решения задач – основной учебной деятельности на уроках математики – развиваются творческая и прикладная стороны мышления.
Обучение алгебре и началам математического анализа дает возможность развивать у учащихся точную, лаконичную и информативную речь, умение отбирать наиболее подходящие языковые (в частности, символические, графические) средства, т.е. способствует формированию коммуникативной культуры, в том числе – умению ясно, логично, точно и последовательно излагать свою точку зрения, использовать языковые средства, адекватные обсуждаемой проблеме.
Дальнейшее развитие приобретут и познавательные действия. Учащиеся глубже осознают основные особенности математики как формы человеческого познания, научного метода познания природы, а также возможные сферы и границы её применения.
Математическое образование вносит свой вклад в формирование общей культуры человека. Необходимыми компонентами общей культуры являются общее знакомство с методами познания действительности, представление о методах математики, их отличия от методов естественных и гуманитарных наук, об особенностях применения математики для решения прикладных задач. Изучение математики способствует эстетическому воспитанию человека, пониманию красоты и изящества математических рассуждений.
История развития математического знания дает возможность пополнить запас историко-научных знаний школьников, сформировать у них представления о математике как части общечеловеческой культуры. Знакомство с основными историческими вехами возникновения и развития математической науки, с историей великих открытий, именами людей, творивших науку, должно войти в интеллектуальный багаж каждого культурного человека.
ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ ОСВОЕНИЯ УЧЕБНОГО ПРЕДМЕТА
Учащиеся должны знать / понимать:
значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике, для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
вероятностный характер различных процессов окружающего мира.
Алгебра
Учащиеся должны уметь:
выполнять арифметические действия, сочетая устные и письменные приемы, применяя вычислительные устройства; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования.
Учащиеся должны использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, обращаясь при необходимости к справочным материалам и применяя простейшие вычислительные устройства.
Функции и графики
Учащиеся должны уметь:
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функции;
описывать по графику и в простейших случаях по формуле поведения и свойства функции;
находить по графику функции наибольшие и наименьшие значения;
решать уравнения, простейшие системы уравнений, используя свойства функции и их графики;
исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функции, строить графики многочленов и простейших рациональных функции с использованием аппарата математического анализа.
Учащиеся должны использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
описания с помощью функции различных зависимостей, представления их графически, интерпретации графиков.
Начала математического анализа
Учащиеся должны уметь:
вычислять производные и первообразные элементарных функции, используя справочные материалы;
вычислять в простейших случаях площади с использованием первообразной.
Учащиеся должны использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решение прикладных задач, в том числе социально-экономических и физических, на вычисление наибольшие и наименьших значений, на нахождение скорости и ускорения.
Уравнения и неравенства
Учащиеся должны уметь:
решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы;
составлять уравнения и неравенства по условию задачи;
использовать графический метод для приближенного решения уравнений и неравенств;
изображать на координатной плоскости множества решений простейших уравнений и их систем.
Учащиеся должны использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Элементы комбинаторики, статистики и теории вероятностей
Учащиеся должны уметь:
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул;
вычислять в простейших случаях вероятности событий на основе подсчета числа исходов.
Учащиеся должны использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
анализа реальных числовых данных, представленных в виде диаграмм, графиков;
анализа информации статистического характера.
СОДЕРЖАНИЕ УЧЕБНОГО ПРЕДМЕТА
1. Тригонометрические функции
Область определения и множество значений тригонометрических функций. Чётность, нечётность, периодичность тригонометрических функций. Свойства и графики функций 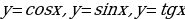 .
.
Основные цели:
- расширить и закрепить знания и умения, связанные с тождественными преобразованиями тригонометрических выражений;
- изучить свойства тригонометрических функций и познакомить учащихся с их графиками.
Изучение темы начинается с вводного повторения, в ходе которого напоминаются основные формулы тригонометрии, известные из курса алгебры, и выводятся некоторые новые формулы. От учащихся не требуется точного запоминания всех формул. Предполагается возможность использования различных справочных материалов: учебника, таблиц, справочников.
Особое внимание следует уделить работе с единичной окружностью. Она становится основой для определения синуса и косинуса числового аргумента и используется далее для вывода свойств тригонометрических функций и решения тригонометрических уравнений.
Систематизируются сведения о функциях и графиках, вводятся новые понятия, связанные с исследованием функций (экстремумы, периодичность), и общая схема исследования функций. В соответствии с этой общей схемой проводится исследование функций синус, косинус, тангенс и строятся их графики.
В результате изучения темы учащиеся должны:
знать:
область определения и множество значений элементарных тригонометрических функций;
тригонометрические функции, их свойства и графики.
уметь:
находить область определения и множество значений тригонометрических функций;
множество значений тригонометрических функций вида kf(x) , где f(x) - любая тригонометрическая функция;
доказывать периодичность функций с заданным периодом;
исследовать функцию на чётность и нечётность;
строить графики тригонометрических функций;
совершать преобразование графиков функций, зная их свойства;
решать графически простейшие тригонометрические уравнения и неравенства.
2. Производная и её геометрический смысл
Производная. Производная степенной функции. Правила дифференцирования. Производные некоторых элементарных функций. Геометрический смысл производной.
Основные цели:
- ввести понятие производной;
- научить находить производные функций в случаях, не требующих трудоемких выкладок.
При введении понятия производной и изучении ее свойств следует опираться на наглядно-интуитивные представления учащихся о приближении значений функции к некоторому числу, о приближении участка кривой к прямой линии и т. п.
Формирование понятия предела функции, а также умение воспроизводить доказательства каких-либо теорем в данном разделе не предусматриваются. В качестве примера вывода правил нахождения производных в классе рассматривается только теорема о производной суммы, все остальные теоремы раздела принимаются без доказательства. Важно отработать достаточно свободное умение применять эти теоремы в несложных случаях.
В ходе решения задач на применение формулы производной сложной функции можно ограничиться случаем 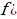 ), именно этот случай необходим далее.
), именно этот случай необходим далее.
В результате изучения темы учащиеся должны:
знать:
понятие производной функции, физического и геометрического смысла производной;
понятие производной степени, корня;
правила дифференцирования;
формулы производных элементарных функций;
уравнение касательной к графику функции;
алгоритм составления уравнения касательной.
уметь:
вычислять производную степенной функции и корня;
находить производные суммы, разности, произведения, частного;
производные основных элементарных функций;
находить производные элементарных функций сложного аргумента;
составлять уравнение касательной к графику функции по алгоритму.
3. Применение производной к исследованию функций
Возрастание и убывание функции. Экстремумы функции. Применение производной к построению графиков функции. Наибольшее и наименьшее значения функции. Выпуклость графика функции, точки перегиба.
Основные цели:
- ознакомить с простейшими методами дифференциального исчисления;
- выработать умение применять их для исследования функций и построения графиков.
Опора на геометрический и механический смысл производной делает интуитивно ясными критерии возрастания и убывания функций, признаки максимума и минимума.
Основное внимание должно быть уделено разнообразным задачам, связанным с использованием производной для исследования функций. Остальной материал (применение производной к приближенным вычислениям, производная в физике и технике) дается в ознакомительном плане.
В результате изучения темы учащиеся должны:
знать:
понятие стационарных, критических точек, точек экстремума;
как применять производную к исследованию функций и построению графиков;
как исследовать в простейших случаях функции на монотонность, находить наибольшее и наименьшее значения функции.
уметь:
находить интервалы возрастания и убывания функций;
строить эскиз графика непрерывной функции, определённой на отрезке;
находить стационарные точки функции, критические точки и точки экстремума;
применять производную к исследованию функций и построению графиков;
находить наибольшее и наименьшее значение функции.
4. Интеграл
Первообразная. Правила нахождения первообразных. Площадь криволинейной трапеции и интеграл. Вычисление интегралов. Вычисление площадей с помощью интегралов.
Основные цели:
- ознакомить с интегрированием как операцией, обратной дифференцированию;
- показать применение интеграла к решению геометрических задач.
Задача отработки навыков нахождения первообразных не ставится, упражнения сводятся к простому применению таблиц и правил нахождения первообразных.
Интеграл вводится на основе рассмотрения задачи о площади криволинейной трапеции и построения интегральных сумм. Формула Ньютона — Лейбница вводится на основе наглядных представлений.
В качестве иллюстрации применения интеграла рассматриваются только задачи о вычислении площадей и объемов. Следует учесть, что формула объема шара выводится при изучении данной темы и используется затем в курсе геометрии.
Материал, касающийся работы переменной силы и нахождения центра масс, не является обязательным.
При изучении темы целесообразно широко применять графические иллюстрации.
В результате изучения темы учащиеся должны:
знать:
понятие первообразной, интеграла;
правила нахождения первообразных;
таблицу первообразных;
формулу Ньютона - Лейбница;
правила интегрирования;
уметь:
проводить информационно-смысловой анализ прочитанного текста в учебнике, участвовать в диалоге, приводить примеры; аргументировано отвечать на поставленные вопросы, осмысливать ошибки и их устранять;
доказывать, что данная функция является первообразной для другой данной функции;
находить одну из первообразных для суммы функций и произведения функции на число, используя справочные материалы;
выводить правила отыскания первообразных;
изображать криволинейную трапецию, ограниченную графиками элементарных функций;
вычислять интеграл от элементарной функции простого аргумента по формуле Ньютона - Лейбница с помощью таблицы первообразных и правил интегрирования;
вычислять площадь криволинейной трапеции, ограниченной прямыми x = a, х = b, осью Ох и графиком квадратичной функции;
находить площадь криволинейной трапеции, ограниченной параболами;
вычислять путь, пройденный телом от начала движения до остановки, если известна его скорость.
5. Элементы математической статистики, комбинаторики и теории вероятностей
Табличное и графическое представление данных. Числовые характеристики рядов данных. Поочередный и одновременный выбор нескольких элементов из конечного множества. Формулы числа перестановок, сочетаний, размещений. Решение комбинаторных задач. Формула бинома Ньютона. Свойства биномиальных коэффициентов. Треугольник паскаля. Элементарные и сложные события. Рассмотрение случаев: вероятность суммы несовместных событий, вероятность противоположного события. Понятие о независимости событий. Вероятность и статистическая частота наступления события. Решение практических задач с применением вероятностных методов. Случайные величины. Центральные тенденции. Меры разброса. Решение практических задач по теме «Статистика».
Основные цели:
- формирование представлений о научных, логических, комбинаторных методах решения математических задач;
- формирование представления о теории вероятности, о понятиях: вероятность, испытание, событие (невозможное, достоверное, случайное), вероятность событий, объединение и пересечение событий, следствие события, независимость событий;
- формирование умения вычислять вероятность событий, определять несовместные и противоположные события;
- овладение умением выполнять основные операции над событиями;
- овладение навыками решения практических задач с применением вероятностных методов.
В результате изучения темы учащиеся должны:
знать:
понятие комбинаторной задачи и основных методов её решения (перестановки, размещения, сочетания без повторения и с повторением);
понятие логической задачи;
приёмы решения комбинаторных, логических задач;
элементы графового моделирования;
понятие вероятности событий;
понятие невозможного и достоверного события;
понятие независимых событий;
понятие условной вероятности событий;
уметь:
использовать основные методы решения комбинаторных, логических задач;
разрабатывать модели методов решения задач, в том числе и при помощи графового моделирования;
переходить от идеи задачи к аналогичной, более простой задаче, т.е. от основной постановки вопроса к схеме;
ясно выражать разработанную идею задачи;
вычислять вероятность событий;
определять равновероятные события;
выполнять основные операции над событиями;
доказывать независимость событий;
находить условную вероятность;
решать практические задачи, применяя методы теории вероятности.
6. Обобщающее повторение курса алгебры и начал математического анализа за 10-11 классы
Числа и алгебраические преобразования. Уравнения. Неравенства. Системы уравнений и неравенств. Производная функции и её применение к решению зада. Функции и графики. Текстовые задачи. Комбинаторика, теория вероятностей, статистика.
Основная цель:
- обобщение и систематизация курса алгебры и начал математического анализа за 10-11 классы.
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
по алгебре и началам математического анализа (102 ч.)
| № п/п | Тема урока | Количество часов | Дата |
| План | Факт |
|
| Повторение | 6 |
|
|
| 1 | Повторение по теме: «Иррациональные уравнения, неравенства» | 1 |
|
|
| 2 | Повторение по теме: «Показательные уравнения, неравенства» | 1 |
|
|
| 3 | Повторение по теме: «Логарифмические уравнения, неравенства» | 1 |
|
|
| 4 | Повторение по теме: «Тригонометрические формулы» | 1 |
|
|
| 5 | Повторение по теме: «Тригонометрические уравнения, неравенства» | 1 |
|
|
| 6 | Контрольная работа (входная диагностика) | 1 |
|
|
|
| Тригонометрические функции | 12 |
|
|
| 7 | Область определения и множество значений тригонометрических функций. | 1 |
|
|
| 8 | Четность, нечетность, периодичность тригонометрических функций | 1 |
|
|
| 9 | Свойства функции 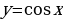 и её график и её график | 1 |
|
|
| 10 | Свойства функции 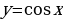 и её график и её график | 1 |
|
|
| 11 | Свойства функции 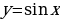 и её график и её график | 1 |
|
|
| 12 | Свойства функции 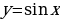 и её график и её график | 1 |
|
|
| 13 | Самостоятельная работа по теме: «Свойства функций 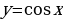 , , 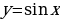 и их графики» и их графики» | 1 |
|
|
| 14 | Свойства функции 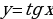 и её график и её график | 1 |
|
|
| 15 | Свойства функции 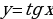 и её график и её график | 1 |
|
|
| 16 | Обратные тригонометрические функции | 1 |
|
|
| 17 | Урок обобщения и систематизации знаний | 1 |
|
|
| 18 | Контрольная работа № 1 по теме: «Тригонометрические функции» | 1 |
|
|
|
| Производная и её геометрический смысл | 17 |
|
|
| 19 | Производная. Работа над ошибками | 1 |
|
|
| 20 | Производная степенной функции | 1 |
|
|
| 21 | Производная степенной функции | 1 |
|
|
| 22 | Правила дифференцирования. Производная суммы | 1 |
|
|
| 23 | Правила дифференцирования. Производная произведения и частного | 1 |
|
|
| 24 | Правила дифференцирования. Производная сложной функции | 1 |
|
|
| 25 | Самостоятельна работа по теме: «Правила дифференцирования» | 1 |
|
|
| 26 | Производные некоторых элементарных функций. Производная показательной функции | 1 |
|
|
| 27 | Производные некоторых элементарных функций. Производная логарифмической функции | 1 |
|
|
| 28 | Производные некоторых элементарных функций. Производные тригонометрических функций | 1 |
|
|
| 29 | Самостоятельная работа по теме: «Производные некоторых элементарных функций» | 1 |
|
|
| 30 | Применение правил дифференцирования и формул производных к решению задач | 1 |
|
|
| 31 | Геометрический смысл производной | 1 |
|
|
| 32 | Геометрический смысл производной. Нахождение углового коэффициента | 1 |
|
|
| 33 | Геометрический смысл производной. Уравнение касательной | 1 |
|
|
| 34 | Урок обобщения и систематизации знаний | 1 |
|
|
| 35 | Контрольная работа № 2 по теме: «Производная и её геометрический смысл» | 1 |
|
|
|
| Применение производной к исследованию функций | 13 |
|
|
| 36 | Возрастание и убывание функций. Работа над ошибками | 1 |
|
|
| 37 | Возрастание и убывание функции. Решение задач | 1 |
|
|
| 38 | Экстремумы функции | 1 |
|
|
| 39 | Экстремумы функции. Решение задач | 1 |
|
|
| 40 | Применение производной к построению графиков функций | 1 |
|
|
| 41 | Построение графиков функций с помощью производной | 1 |
|
|
| 42 | Построение графиков функций с помощью производной | 1 |
|
|
| 43 | Наибольшее и наименьшее значение функции | 1 |
|
|
| 44 | Нахождение наибольшего и наименьшего значений функции | 1 |
|
|
| 45 | Самостоятельная работа по теме: «Наибольшее и наименьшее значения функции» | 1 |
|
|
| 46 | Выпуклость графика функции, точки перегиба | 1 |
|
|
| 47 | Контрольная работа № 3 по теме: «Применение производной к исследованию функций» | 1 |
|
|
| 48 | Анализ контрольной работы. Работа над ошибками | 1 |
|
|
|
| Интеграл | 11 |
|
|
| 49 | Первообразная | 1 |
|
|
| 50 | Правила нахождения первообразных | 1 |
|
|
| 51 | Правила нахождения первообразных. Решение задач | 1 |
|
|
| 52 | Площадь криволинейной трапеции и интеграл | 1 |
|
|
| 53 | Площадь криволинейной трапеции. Решение задач | 1 |
|
|
| 54 | Вычисление интегралов | 1 |
|
|
| 55 | Вычисление интегралов. Решение задач | 1 |
|
|
| 56 | Вычисление площадей с помощью интегралов | 1 |
|
|
| 57 | Вычисление площадей с помощью интегралов. Решение практических задач | 1 |
|
|
| 58 | Урок обобщения и систематизации знаний | 1 |
|
|
| 59 | Контрольная работа № 4 по теме: «Интеграл» | 1 |
|
|
|
| Комбинаторика | 10 |
|
|
| 60 | Правило произведения. Работа над ошибками | 1 |
|
|
| 61 | Перестановки | 1 |
|
|
| 62 | Размещения | 1 |
|
|
| 63 | Сочетания и их свойства | 1 |
|
|
| 64 | Решение комбинаторных задач | 1 |
|
|
| 65 | Биномиальная формула Ньютона. Бином Ньютона | 1 |
|
|
| 66 | Свойства биномиальных коэффициентов | 1 |
|
|
| 67 | Треугольник Паскаля | 1 |
|
|
| 68 | Урок обобщения и систематизации знаний | 1 |
|
|
| 69 | Контрольная работа № 5 по теме: «Комбинаторика» | 1 |
|
|
|
| Элементы теории вероятностей | 9 |
|
|
| 70 | События. Элементарные и сложные события. Работа над ошибками | 1 |
|
|
| 71 | Комбинация событий. Противоположное событие | 1 |
|
|
| 72 | Вероятность события. Вероятность и статистическая частота наступления события | 1 |
|
|
| 73 | Сложение вероятностей. Вероятность суммы несовместных событий, вероятность противоположного события | 1 |
|
|
| 74 | Независимые события. Умножение вероятностей | 1 |
|
|
| 75 | Статистическая вероятность. Решение практических задач с применением вероятностных методов | 1 |
|
|
| 76 | Статистическая вероятность. Решение практических задач с применением вероятностных методов | 1 |
|
|
| 77 | Контрольная работа № 6 по теме: «Элементы теории вероятностей» | 1 |
|
|
| 78 | Анализ контрольной работы. Работа над ошибками | 1 |
|
|
|
| Статистика | 6 |
|
|
| 79 | Случайные величины | 1 |
|
|
| 80 | Центральные тенденции | 1 |
|
|
| 81 | Меры разброса | 1 |
|
|
| 82 | Решение практических задач по теме «Статистика» | 1 |
|
|
| 83 | Урок обобщения и систематизации знаний | 1 |
|
|
| 84 | Контрольная работа № 7 по теме: «Статистика» | 1 |
|
|
|
| Обобщающее повторение курса алгебры и начал математического анализа за 10-11 классы | 18 |
|
|
| 85 | Числа и алгебраические преобразования. Работа над ошибками | 1 |
|
|
| 86 | Числа и алгебраические преобразования | 1 |
|
|
| 87 | Решение уравнений | 1 |
|
|
| 88 | Решение уравнений | 1 |
|
|
| 89 | Решение неравенств | 1 |
|
|
| 90 | Решение неравенств | 1 |
|
|
| 91 | Решение систем уравнений и неравенств | 1 |
|
|
| 92 | Решение систем уравнений и неравенств | 1 |
|
|
| 93 | Решение текстовых задач | 1 |
|
|
| 94 | Решение текстовых задач | 1 |
|
|
| 95 | Производная функции и её применение к решению задач | 1 |
|
|
| 96 | Производная функции и её применение к решению задач | 1 |
|
|
| 97 | Функции и графики | 1 |
|
|
| 98 | Функции и графики | 1 |
|
|
| 99 | Комбинаторика, теория вероятностей, статистика | 1 |
|
|
| 100 | Комбинаторика, теория вероятностей, статистика | 1 |
|
|
| 101 | Итоговая контрольная работа | 1 |
|
|
| 102 | Анализ итоговой контрольной работы | 1 |
|
|
|
| Итого | 102 |
|
|
МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ОБРАЗОВАТЕЛЬНОГО ПРОЦЕССА
Учебно–программные материалы:
Алгебра и начала математического анализа. Сборник рабочих программ. 10-11 классы: учеб. пособие для учителей общеобразоват. организаций: базовый и углубл. уровни / [сост. Т. А. Бурмистрова]. – 2-е изд., перераб. – М.: Просвещение, 2018.
Учебно-теоретические материалы:
Учебник: Алгебра и начала математического анализа. 10-11 классы: учеб. для общеобразоват. учреждений: базовый уровень / [Ш. А. Алимов, Ю. М. Колягин, М. В. Ткачев и др.]. – М.: Просвещение, 2015.
Учебно-практические материалы:
Газета «Математика» - приложение к газете «Первое сентября»;
А.П.Ершова «Алгебра и начала анализа 10-11 классы. Самостоятельные и контрольные работы», М., «Илекса»,2003;
Денищева Л.О. «Тематический контроль по алгебре и началам анализа 10-11 классы», М., «Интеллект-центр», 2005;
Старостенкова Н.Г. «Проверочные работы с элементами тестирования по алгебре 11 класс», Саратов, «Лицей», 2003;
Афанасьева Т.Л. Алгебра и начала анализа 11 класс. Поурочные планы. Волгоград, «Учитель», 2002.
Интернет – ресурсы:
Я иду на урок математики (методические разработки). – Режим доступа: www.festival. l september.ru;
Уроки, конспекты. – Режим доступа: www.pedsovet.ru.
Информационно-коммуникативные средства:
Коллекция мультимедийных уроков Кирилла и Мефодия (CD).
Наглядные пособия:
Портреты великих ученых-математиков;
Демонстрационные таблицы.
Технические средства обучения:
Компьютер;
Видеопроектор.





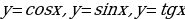 .
.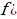 ), именно этот случай необходим далее.
), именно этот случай необходим далее.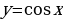 и её график
и её график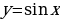 и её график
и её график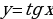 и её график
и её график









