Рабочая программа «Олимпиадная математика »

Муниципальное общеобразовательное учреждение

«Средняя школа №91 «Центр инженерных технологий»

(Центр дополнительного образования «SREDA»)

Принято на Педагогическом совете Протокол № 6 от 30.08.2022 г.

Утверждаю: Директор МОУ «Средняя школа №91 «ИнТех» ______________ С.Н. Кангина Приказ №04-06/1 от 31.08.2022 г.

Дополнительная общеобразовательная общеразвивающая программа

«Олимпиадная математика «Петерсон Л. Г.»»

Возраст обучающихся: 11-12 лет

Срок реализации: 9 месяцев

Направленность: естественнонаучная

Автор - составитель:

Карташова Н. С,

педагог дополнительного образования

Ярославль,

2024 г.

Оглавление

I.Пояснительная записка……………………………………………………3

II. Учебный план ……………………………………………………………6

III.Содержание образовательной программы…………………………… 8

IV. Ожидаемые результаты освоения программы……………………… 11

V. Контрольно-измерительные материалы………………………………. 11

Список литературы……………………………………………………… 12

I.Пояснительная записка

Нормативно-правовая основа для разработки программы

Настоящая дополнительная общеобразовательная общеразвивающая программа далее (программа) разработана в соответствии со следующими документами:

1. Федеральный Закон от 29.12.2012г. № 273-ФЗ «Об образовании в Российской Федерации»;

2. Федеральный закон РФ от 24.07.1998 №124 ФЗ «Об основных гарантиях прав ребенка в Российской Федерации»;

3. Стратегия развития воспитания в РФ на период до 2025 года (распоряжение Правительства РФ от 29 мая 2015 год, №996-з);

4. Концепция развития дополнительного образования детей до 2030 года и план мероприятий по ее реализации (Распоряжение Правительства РФ от 31 марта 2022 г. № 678-р);

5. Постановление Главного государственного санитарного врача РФ от 28.09.2020 N 28 «Об утверждении санитарных правил СП 2.4.3648-20 «Санитарно-эпидемиологические требованиям к организациям воспитания и обучения, отдыха и оздоровления детей и молодежи»;

6. Паспорт федерального проекта «Успех каждого ребенка» (утвержден на заседании проектного комитета по национальному проекту «Образование» 07 декабря 2018 г., протокол №3);

7. Приказ Министерства просвещения Российской Федерации от 03.09.2019 г. №467 «Об утверждении целевой модели развития региональных систем дополнительного образования детей»;

8. Приказ Министерства образования и науки Российской Федерации от 23.08.2017 г. №816 «Об утверждении Порядка применения организациями, осуществляющими образовательную деятельность, электронного обучения, дистанционных образовательных технологий при реализации образовательных программ»;

9. Приказ Министерства труда и социальной защиты Российской Федерации от 05.05.2018 г. №298 «Об утверждении профессионального стандарта “Педагог дополнительного образования детей и взрослых”»;

10. Приказ Министерства образования и науки Российской Федерации и Министерства просвещения Российской Федерации от 05.08.2020 г. №882/391 «Об организации и осуществлении образовательной деятельности по сетевой форме реализации образовательных программ»;

11. Приказ Департамента образования Ярославской области от 07.08.2018 г. №19-нп «Об утверждении Правил персонифицированного финансирования детей в Ярославской области»;

12. Устав МОУ «Средняя школа №91 «ИнТех».

Математические олимпиады в настоящее время принято считать элитным направлением: в них вовлечено ограниченное число школьников, чаще всего из математических классов или профильных образовательных организаций. При этом мощный ресурс олимпиадной математики как эффективного инструмента интеллектуального и личностного развития детей в массовой школе используется недостаточно.

Олимпиадные задачи — это, как правило, нестандартные задачи, поэтому для их решения недостаточно просто применить приобретенные на уроках знания и умения. Решение любой олимпиадной задачи — это всегда пусть маленькое, но открытие, демонстрирующее красоту математической мысли и позволяющее пережить радость творчества и удовольствие от интеллектуальной деятельности. Решение олимпиадных задач развивает у каждого ребенка глубину и гибкость мышления, воображение, самостоятельность и трудолюбие, творческие способности, повышает интерес к математике и уровень математической подготовки. Поэтому вовлечение в олимпиадную математику важно для всех учеников: математически одаренные дети в творческой среде смогут полнее реализовать свой потенциал и вырастить свой математический талант, сохраняя физическое и психическое здоровье, а все остальные — развить свои математические способности и успешнее учиться, что пригодится в любом деле.

Актуальность программы определяется запросом со стороны детей и их родителей на программы развития логического мышления

Направленность программы: естественнонаучная

Цель: системная подготовка учащихся 5 классов к математическим олимпиадам, ориентированная на вовлечение школьников в математическую деятельность, развитие мотивации, мышления, творческих способностей и за счет этого — достижение более высокого уровня их олимпиадной и общей математической подготовки.

Задачи:

Обучающие

1. Обучение навыкам и приемам решения нестандартных математических задач, которые не рассматриваются на уроках математики

2. Знакомство с исследовательской деятельностью, способами проведения экспериментов и обобщения;

Развивающие

1. Развитие математического, логического мышления

2. Развитие творческих способностей

3. Развитие нестандартного мышления

Воспитательные

1. Воспитание чувства товарищества

2. Расширение и углубление представлений учащихся о культурно-исторической ценности математики, о роли ведущих учёных- математиков в развитии мировой науки;

Новизна, отличительные особенности программы

1. мотивация и вовлечение учащихся в самостоятельную математическую деятельность на основе системно-деятельностного подхода;

2. выращивание общеучебных интеллектуальных умений, необходимых для решения олимпиадных задач: умения эффективно преодолевать трудности, владения общими подходами к решению нестандартных задач, умения работать в команде и др.;

3. создание творческой, эмоционально окрашенной образовательной среды, где каждый ученик имеет возможность добиться успеха;

Категория обучающихся: 11-12 лет

Количество обучающихся: 7 - 15 детей

Продолжительность обучения: 9 месяцев

Место реализации образовательной программы: Центр дополнительного образования МОУ «Средняя школа №91 «ИнТех», расположенный по адресу: Дядьковский проезд, здание 8.

Условия реализации программы

Организационные условия:

Материально-технические условия реализации программы: учебный кабинет, раздаточный материал, презентации

Кадровые:

Карташова Наталья Сергеевна, учитель математики, высшая квалификационная категория

Методическое обеспечение программы:

1. Раздаточный материал

2.Презентации

II. Учебный план

Занятия проводятся 1 раз в неделю в течение 2024-2025 учебного года. Продолжительность одного занятия 40 минут, что составляет 1 академический час. Всего занятий 34. Всего часов 34 .

№	Тема раздела	Всего часов	Из них
			Теория	Практика
	Магический квадрат	2	1	1
	Переправы	2	1	1
	Остров рыцарей и лжецов	2	1	1
	Метод перебора	2	1	1
	Буквенные ребусы	2	1	1
	Дни недели	2	1	1
	Эффект «плюс-минус один»	2	1	1
	Площадь на клетчатой бумаге	2	1	1
	Малые случаи	2	1	1
	Разрезания по диагоналям клеток	2	1	1
	Четность суммы чисел	2	1	1
	Чередование	2	1	1
	По прямой — кратчайший путь!	2	1	1
	Учти лишнее	2	1	1
	Шахматная доска	2	1	1
	Изобрази множество	2	1	1
	Нарисовать одним росчерком	2	1	1
	Итого	34	17	17

Календарно-тематический график

№	Тема занятия	Кол-во часов
	Магический квадрат	1
	Подсчет двумя способами в арифметических задачах, конструкции с натуральными числами	1
	Переправы	1
	Конструирование арифметических алгоритмов, алгоритмы с наименьшим количеством действий	1
	Остров рыцарей и лжецов	1
	Остров рыцарей и лжецов. Решение задач	1
	Метод перебора	1
	Метод перебора в логических задачах, использование отрицаний простейших высказываний	1
	Буквенные ребусы	1
	Метод перебора в арифметических задачах, доказательство отсутствия решения (с помощью оценок, перебора вариантов, четности)	1
	Дни недели	1
	Недельная и годовая цикличность, день недели как остаток от деления на 7	1
	Эффект «плюс-минус один»	1
	Методы преодоления эффекта «плюс-минус один» (графический, раз биение на пары)	1
	Площадь на клетчатой бумаге	1
	Разбиения фигур на клетчатой бумаге на элементарные части для вычисления их площади	1
	Малые случаи	1
	Разделение задачи на эквивалентные подзадачи, метод проверки ответа (закономерности, формулы) на малых случаях	1
	Разрезания по диагоналям клеток	1
	Вспомогательный подсчет площади в задачах на разрезание не по линиям сетки, метод перебора	1
	Четность суммы чисел	1
	Критерий четности суммы ряда чисел, четность произведения двух чисел	1
	Чередование	1
	Чередование объектов в ряду, по кругу. Относительное количество чередующихся объектов. Четность суммы чисел в промежутке. Связь чередования и разбиения на пары	1
	По прямой — кратчайший путь!	1
	Приближенное вычисление длин ломаных и кривых, кратчайшие пути на развертках	1
	Учти лишнее	1
	Метод «учти лишнее» при решении арифметических задач	1
	Шахматная доска	1
	Конструкции с шахматной доской, идея доказательства невозможности разрезания	1
	Изобрази множество	1
	Действия с множествами с неизвестным количеством элементов, методы решения задач про множества с процентами, долями и дробями	1
	Нарисовать одним росчерком	1
	Использование степеней вершин в графе для проверки, можно ли на рисовать фигуру одним росчерком, и нахождения концов росчерка	1

III.Содержание образовательной программы

Раздел 1 «Магический квадрат»

Теория:

-история появления магических квадратов

-виды магических квадратов

Практика:

-построение магических квадратов

-подсчет двумя способами в арифметических задачах

-конструкции с натуральными числами

Раздел 2 «Переправы»

Теория:

-Историческая справка

-Пути решения задач на переправы, переезды

Практика:

-конструирование арифметических алгоритмов

-построение алгоритмов с наименьшим количеством действий

Раздел 3 «Остров рыцарей и лжецов»

Теория:

-Справка о типах задач «Рыцари и лжецы»

-алгоритмы, применяемые при решении задач о «Рыцарях и лжецах»

Практика:

-применение метода перебора в логических задачах

-использование отрицания в простейших высказываниях

Раздел 4 «Метод перебора»

Теория:

-метод перебора

Практика:

-сравнение перебора в текстовых задачах к перебору малого числа вариантов

-доказательство нахождения всех решений

Раздел 5 «Буквенные ребусы»

Теория:

-Понятие буквенного ребуса

-правила разгадывания ребусов

Практика:

-применение метода перебора при решении буквенного ребуса

Раздел 6 «Дни недели»

Теория:

-недельная и годовая цикличность

-день недели как остаток от деления на 7

Практика:

-решение задач на цикличность

-решение задач на деление с остатком

Раздел 7 «Эффект «плюс-минус один»»

Теория:

- Справка Эффект «плюс-минус один»

- когда применять Эффект «плюс-минус один»

-методы преодоления эффекта «плюс-минус один»

-графический метод

-метод разбиения на пары

Практика:

-решение задач

- построение графиков и схем

-разбиение на пары

Раздел 8 «Площадь на клетчатой бумаге»

Теория:

-Справка. Почему задачи так назвали?

-приемы и методы решения задач на клетчатой бумаге

Практика:

-использование разбиения фигур на клетчатой бумаге на элементарные части для вычисления их площади

Раздел 9 «Малые случаи»

Теория:

-виды задач

-что такое малый случай в математике

Практика:

-разделение задачи на эквивалентные подзадачи

-метод проверки ответа на малых случаях

Раздел 10 «Разрезание по диагоналям клеток»

Теория:

-справка: задачи на разрезание

-приемы решения задач на разрезания

-метод перебора

Практика:

-решение задач путем разрезания фигуры

Раздел 11 «Четность суммы»

Теория:

-критерии четности суммы ряда чисел

-четность произведения двух чисел

Практика:

-решение задач на четность

Раздел 12 «Чередование»

Теория:

-чередование в математике

-виды чередований: по кругу, в ряду

-связь чередования и разбиение на пары

Практика:

-применение метода чередования при решении математических задач

Раздел 13 «По прямой- кратчайший путь!»

Теория:

-понятие ломанной, кривой

-кратчайший путь на развертках

Практика:

-решение задач с развертками

-вычисление длин ломанных и кривых

Раздел 14 «Учти лишнее»

Теория:

-метод «учти лишнее»

-метод дополнения

Практика:

-применение методов при решении арифметических задач

Раздел 15 «Шахматная доска»

Теория:

-идеи доказательства и решения задач с шахматной доской

Практика:

-работа с конструкциями на шахматной доске

-применение новых идей и доказательств

Раздел 16 «Изобрази множество»

Теория:

-понятие множества

-историческая справка

-символы, обозначения и операции над множествами

Практика:

-изображение множеств на языке математики

Раздел 17 «Нарисовать одним росчерком»

Теория:

-понятие графа

-что такое росчерк

-степень вершины в графе

-способы проверки возможности нарисовать фигуру одним росчерком

Практика:

-построение «рисунка» одним росчерком

IV. Ожидаемые результаты освоения программы

  Личностными результатами изучения курса является формирование следующих умений:

Определять и высказывать самые простые общие для всех людей правила поведения при сотрудничестве (этические нормы).

В предложенных педагогом ситуациях общения и сотрудничества, опираясь на общие для всех простые правила поведения, делать выбор, при поддержке других участников группы и педагога, как поступить. Для оценки формирования и развития личностных характеристик воспитанников (ценности, интересы, склонности, деловые качества воспитанника) используется простое наблюдение, проведение математических игр.

        Метапредметными результатами изучения курса в 5-м классе является формирование универсальных учебных действий (УУД).

        Для отслеживания уровня усвоения программы и своевременного внесения коррекции целесообразно использовать следующие формы контроля: занятия-конкурсы на повторение практических умений, занятия на повторение и обобщение (после прохождения основных разделов программы), самопрезентация (просмотр работ с их одновременной защитой), участие в математических олимпиадах и конкурсах различного уровня.

        Кроме того, необходимо систематическое наблюдение за обучающимися в течение учебного года, включающее: результативность и самостоятельную деятельность ребенка, активность, аккуратность, творческий подход к знаниям, степень самостоятельности в их решении и выполнении и т.д.

        Предметными результатами изучения курса является формирование следующих умений:

 - описывать признаки предметов и узнавать предметы по их признакам;

 - выделять существенные признаки предметов;

 - сравнивать между собой предметы, явления; - обобщать, делать несложные выводы;

- классифицировать явления, предметы;

- определять последовательность событий;

- судить о противоположных явлениях;

- давать определения тем или иным понятиям;

 - выявлять функциональные отношения между понятиями; - выявлять закономерности и проводить аналогии;

- создавать условия, способствующие наиболее полной реализации потенциальных познавательных возможностей всех детей в целом и каждого ребенка в отдельности, принимая во внимание особенности их развития;

- осуществлять принцип индивидуального и дифференцированного подхода в обучении учащихся с разными образовательными возможностями.

V. Контрольно-измерительные материалы

        Проверка результатов проходит в форме: игровых занятий на повторение теоретических понятий, собеседования (индивидуальное и групповое), тестирования, проведения самостоятельных работ и др.

        Занятия рассчитаны на групповую и индивидуальную работу. Они построены таким образом, что один вид деятельности сменяется другим. Это позволяет сделать работу динамичной, насыщенной и менее утомительной, при этом принимать во внимание способности каждого ученика в отдельности, включая его по мере возможности в групповую работу, моделировать и воспроизводить ситуации, трудные для ученика, но возможные в обыденной жизни; их анализ и проигрывание могут стать основой для позитивных сдвигов в развитии личности ребёнка.

Оценивание результатов в курсе «Олимпиадная математика» происходит в логике достижений — не только математических, но и личностных, «относительно себя». При этом для каждого следующего шага ребенку необходимо предпринять определенные усилия, проявить терпение, трудолюбие, но трудность должна быть преодолимой. Обсуждаются

вопросы: «Что получилось?», «Что вызвало затруднение?», «Чему научился, решая (разбирая) задачу?», «Что пожелаю себе?»,

«За что могу похвалить себя, других?». Учитель организует в классе ситуацию взаимной поддержки и совместного переживания радости победы.

Текущий контроль по данному курсу осуществляется в течение всего учебного года. При оценивании работ следует исходить из того, что основной целью подведения итогов в рамках курса «Олимпиадная математика» является формирование положительной мотивации учащихся к решению математических задач. Поэтому обязательным является

соблюдение следующих требований:

1)фиксируются только достижения, а относительно неудач проводится рефлексия и намечается план коррекции;

2)акцент в оценивании смещается на самооценку детьми своих достижений

3)при подведении итогов следует учитывать не только результат, но и вложенные учеником усилия, а также динамику результатов «относительно себя»;

4)по результатам отметки не выставляются.

Основными показателями результативности проводимой работы по курсу «Олимпиадная математика» является возрастание познавательной мотивации учащихся, их участие и результаты в математических олимпиадах разного уровня (в том числе, в обучающей «Олимпиаде Петерсон»), повышение глубины и качества знаний по математике.

Пример самостоятельной работы с последующей самопроверкой по образцу

к разделу «Нарисовать одним росчерком»

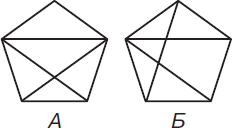
№1 Домики

Какую фигуру, А или Б, можно нарисовать одним росчерком? Ответ объясни.

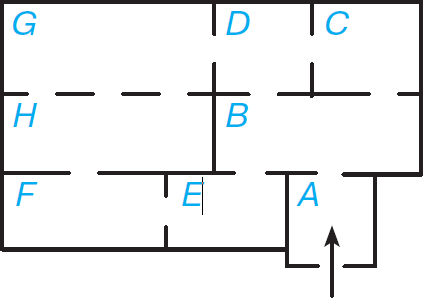
№2. План музея

Перед тобой план музея. Турист обошел все залы и понял, что через каждую дверь он прошел ровно один раз. В каком зале он мог оказаться в конце пути, если зашел с улицы в зал A? Есть ли другие варианты?

№3. И начало, и конец

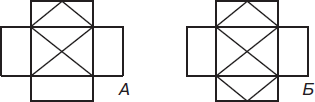Какую фигуру, А или Б, можно нарисовать одним росчерком так, чтобы его начало и конец совпадали?

№4 Богатырская задача

У Ильи Муромца есть стальной прут длиной 240 см. Он хочет похвастаться силушкой, согнув прут в нескольких местах так, чтобы получился каркас куба с ребром 20 см. Объясни, почему богатырь не сможет это сделать, хотя силы у него достаточно. Ломать прут нельзя.

Дополнительные задания

№5. Путь по кубику

Все грани куба с ребром 3 см разделены на квадратики 1 × 1 см. Нарисуй на поверхности этого куба замкнутый путь, проходящий через все маленькие квадратики (кроме самого первого) по одному разу и не пересекающий вершины квадратов.

Эталон для самопроверки

№. Домики

Какую фигуру, А или Б, можно нарисовать одним росчерком? Ответ объясни.

Решение

В фигуре А две нечетные вершины. Ее можно нарисовать одним росчерком, начав в одной из них и закончив в другой (см. рисунок).

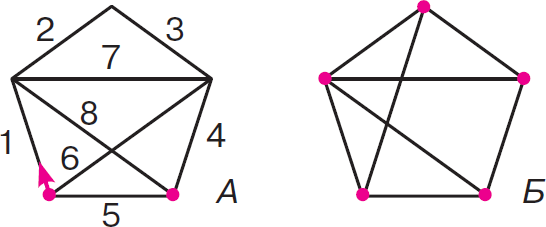В фигуре Б — 4 нечетные вершины, 4 2 ⇒ Фигуру Б нельзя нарисовать одним росчерком Ответ: только фигуру А.

№2. План музея

Перед тобой план музея. Турист обошел все залы и понял, что через каждую дверь он прошел ровно один раз. В каком зале он мог оказаться в конце пути, если зашел с улицы в зал A? Есть ли другие варианты?

Решение

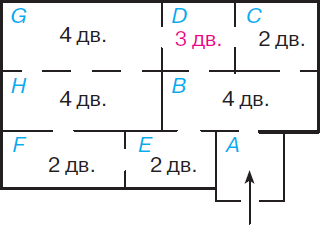При обходе залов турист входит в одну дверь и выходит в другую (парами). Нечетное число дверей (кроме зала А) ведет только из зала D ⇒ Турист мог закончить маршрут только в зале D.

Ответ: в зале D; нет.

№3. И начало, и конец

Какую фигуру, А или Б, можно нарисовать одним росчерком так, чтобы его начало и конец совпадали?

Решение

В фигуре А две нечетные вершины ⇒ Они должны быть началом и концом росчерка ⇒ Начало и конец росчерка не могут совпасть (см. рисунок).

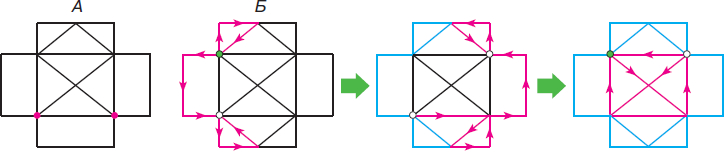Фигуру Б нарисовать можно (см. рисунок).

Ответ: только фигуру Б.

№4*. Богатырская задача

У Ильи Муромца есть стальной прут длиной 240 см. Он хочет похвастаться силушкой, согнув прут в нескольких местах так, чтобы получился каркас куба с ребром 20 см. Объясни, почему богатырь не сможет это сделать, хотя силы у него достаточно. Ломать прут нельзя.

Решение

Из всех вершин куба выходит по 3 линии ⇒ Все 8 вершин куба — нечетные, 8 2 ⇒ Нарисовать куб одним росчерком не получится ⇒ Согнуть такой каркас нельзя.

Дополнительные задания

№5. Путь по кубику

Все грани куба с ребром 3 см разделены на квадратики 1 × 1 см. Нарисуй на поверхности этого куба замкнутый путь, проходящий через все маленькие квадратики (кроме самого первого) по одному разу и не пересекающий вершины квадратов.

Подсказка

Удобно рисовать такой путь на развертке кубика (см. рисунок):

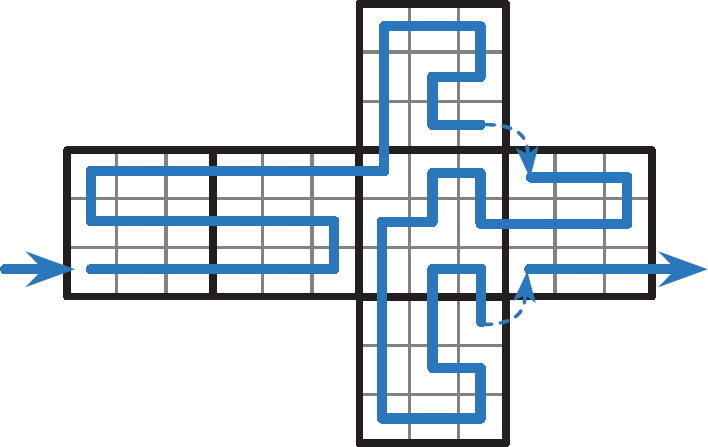
Решение

Возможный пример — на рисунке. Замечание

Существуют и другие примеры.

Список литературы

1.Рабочая концепция одаренности: Федеральная целевая программа «Одаренные дети» / Под ред. Д. Б. Богоявленской, В. Д. Шадрикова. — М.: Министерство образования РФ, 2003. (http://narfu.ru/school/deti_konchep.pdf)

2.Петерсон Л. Г. Система и структура учебной деятельности в контексте современной методологии. Монография / Л. Г. Петерсон, Ю. В. Агапов, М. А. Кубышева и др. — М.: Институт СДП, 2018.

3.Петерсон Л. Г. Деятельностный метод обучения: построение непрерывной сферы образования / Л. Г. Петерсон, М. А. Кубышева и др. — М.: АПК и ППРО; УМЦ «Школа 2000…», 2007.

Интернет-источники:

1. Infourok.ru

2. https://peterson.institute/