МБОУ «Санномыская средняя общеобразовательная школа»
Рассмотрено: Согласовано: Утверждено:
на методическом на педагогическом Приказом директора школы
объединении совете № 65 от 13.05. 2022 г.
Протокол № 8 Протокол № 7
От 06.05.2022 г. от 13.05.2022 г. ___________/Н.В.Рекунова/
Рабочая программа
по предмету
АЛГЕБРА
И НАЧАЛА МАТЕМАТИЧЕСКОГО
АНАЛИЗА
(базовый и профильный уровни)
10 КЛАСС
Учитель математики:
Рекунова Наталья Владимировна
с. Санномыск
2022 г.
Планируемые результаты освоения учебного
предмета Алгебра и начала математического анализа 10 класса
Рабочая программа ориентирована на использование учебника «Алгебра и начала математического анализа 10 класс»: учебник для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. – М.: Вентана – Граф, 2021.
В данной программе на изучение Алгебры и начала математического анализа в 10 классе отводится 4 часа в неделю, из расчета 34 учебных недели – 136 часов.
Результаты освоения программного материала по предмету «Алгебра и начала математического анализа» представлены соответственно личностными, метапреметными и предметными результатами.
Изучение математики в условиях реализации ФГОС дает возможность обучающимся достичь следующих результатов развития:
Личностные результаты:
воспитание российской гражданской идентичности: патриотизма, уважения к Отечеству, осознание вклада отечественных учёных в развитие мировой науки;
формирование мировоззрения, соответствующего современному уровню развития науки и общественной практики;
ответственное отношение к обучению, готовность и способность к саморазвитию и самообразованию на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности;
осознанный выбор будущей профессиональной деятельности на базе ориентировки в мире профессий и профессиональных предпочтений; отношение к профессиональной деятельности как к возможности участия в решении личных, общественных, государственных и общенациональных проблем; формирование уважительного отношения к труду, развитие опыта участия в социально значимом труде;
умение контролировать, оценивать и анализировать процесс и результат учебной и математической деятельности;
умение управлять своей познавательной деятельностью;
умение взаимодействовать с одноклассниками, детьми младшего возраста и взрослыми в образовательной, общественно полезной, учебно-исследовательской, проектной и других видах деятельности;
критичность мышления, инициатива, находчивость, активность при решении математических задач.
Метапредметные результаты:
умение самостоятельно определять цели своей деятельности, ставить и формулировать для себя новые задачи в учёбе;
умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией;
умение самостоятельно принимать решения, проводить анализ своей деятельности, применять различные методы познания;
владение навыками познавательной, учебно-исследовательской и проектной деятельности;
формирование понятийного аппарата, умения создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации;
умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и делать выводы;
формирование компетентности в области использования информационно-коммуникационных технологий;
умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
умение самостоятельно осуществлять поиск в различных источниках, отбор, анализ, систематизацию и классификацию информации, необходимой для решения математических проблем, представлять её в понятной форме; принимать решение в условиях неполной или избыточной, точной или вероятностной информации; критически оценивать и интерпретировать информацию, получаемую из различных источников;
умение использовать математические средства наглядности (графики, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;
умение выдвигать гипотезы при решении задачи, понимать необходимость их проверки;
понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.
Предметные результаты:
Числа и величины
Выпускник научится:
оперировать понятием «радианная мера угла», выполнять преобразования радианной меры в градусную и градусной меры в радианную;
оперировать понятием «комплексное число», выполнять арифметические операции с комплексными числами;
изображать комплексные числа на комплексной плоскости, находить комплексную координату числа.
Выпускник получит возможность научиться:
использовать различные меры измерения углов при решении геометрических задач, а также задач из смежных дисциплин;
применять комплексные числа для решения алгебраических уравнений.
Выражения
Выпускник научится:
оперировать понятиями корня n-й степени, степени с рациональным показателем, степени с действительным показателем, логарифма;
применять понятия корня n-й степени, степени с рациональным показателем, степени с действительным показателем, логарифма и их свойства в вычислениях и при решении задач;
выполнять тождественные преобразования выражений, содержащих корень n-й степени, степени с рациональным показателем, степени с действительным показателем, логарифм;
оперировать понятиями: косинус, синус, тангенс, котангенс угла поворота, арккосинус, арксинус, арктангенс и арккотангенс;
выполнять тождественные преобразования тригонометрических выражений.
Выпускник получит возможность научиться:
выполнять многошаговые преобразования выражений, применяя широкий набор способов и приёмов;
применять тождественные преобразования выражений для решения задач из различных разделов курса
Уравнения и неравенства
Выпускник научится:
решать иррациональные, тригонометрические, показательные и логарифмические уравнения, неравенства и их системы;
решать алгебраические уравнения на множестве комплексных чисел;
понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных реальных ситуаций, решать текстовые задачи алгебраическим методом;
применять графические представления для исследования уравнений.
Выпускник получит возможность научиться:
овладеть приёмами решения уравнений, неравенств и систем уравнений; применять аппарат уравнений для решения разнообразных задач из математики, смежных предметов, практики;
применять графические представления для исследования уравнений, неравенств, систем уравнений, содержащих параметр
Функции
Выпускник научится:
понимать и использовать функциональные понятия, язык (термины, символические обозначения);
выполнять построение графиков функций с помощью геометрических преобразований;
выполнять построение графиков вида y=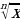 , степенных, тригонометрических, обратных тригонометрических, показательных и логарифмических функций;
, степенных, тригонометрических, обратных тригонометрических, показательных и логарифмических функций;
исследовать свойства функций;
понимать функцию как важнейшую математическую модель для описания процессов и явлений окружающего мира, применять функциональный язык для описания и исследования зависимостей между физическими величинами.
Выпускник получит возможность научиться:
проводить исследования, связанные с изучением свойств функций, в том числе с использованием компьютера;
использовать функциональные представления и свойства функций для рения задач из различных разделов курса математики.
Элементы математического анализа
Выпускник научится:
понимать терминологию и символику, связанную с понятиями производной, первообразной и интеграла;
решать неравенства методом интервалов
вычислять производную и первообразную функции;
использовать производную для исследования и построения графиков функций; понимать геометрический смысл производной и определённого интеграла;
вычислять определённый интеграл.
Выпускник получит возможность научиться:
сформировать представление о пределе функции в точке;
сформировать представление о применении геометрического смысла производной и интеграла в курсе математики, в смежных дисциплинах;
формировать и углубить знания об интеграле.
Вероятность и статистика. Работа с данными
Выпускник научится
решать комбинаторные задачи на нахождение количества объектов или комбинаций;
применять формулу бинома Ньютона для преобразования выражений;
использовать метод математической индукции для доказательства теорем и решения задач;
использовать способы представления и анализа статистических данных;
выполнять операции над событиями и вероятностями.
Выпускник получит возможность научиться:
научиться специальным приёмам решения комбинаторных задач;
характеризовать процессы и явления, имеющие вероятностный характер.
Содержание учебного предмета
Отбор содержания обучения осуществляется на основе следующих дидактических принципов: систематизация знаний, полученных учащимися в основной школе; соответствие обязательному минимуму содержания образования в основной школе; усиление общекультурной направленности материала; учёт психолого-педагогических особенностей, актуальных для этого возрастного периода; создание условий для понимания и осознания воспринимаемого материала. В предлагаемом курсе математики выделяются несколько разделов.
1. Повторение и расширение сведений о функции
Наибольшее и наименьшее значения функции. Чётные и нечётные функции. Свойства графиков чётной и нечётной функций. Построение графиков функций с помощью геометрических преобразований (параллельных переносов, сжатий, растяжений, симметрий). Обратимые функции. Связь возрастания и убывания функции с её обратимостью. Взаимно обратные функции. Свойства графиков взаимно обратных функций.
2. Степенная функция
Степенная функция. Степенная функция с натуральным (целым) показателем. Свойства степенной функции с натуральным (целым) показателем. График степенной функции с натуральным (целым) показателем. Функция y=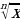 . Взаимообратность функций y=
. Взаимообратность функций y=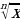 и степенной функции с натуральным показателем. Свойства функции y=
и степенной функции с натуральным показателем. Свойства функции y=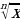 и её график. Иррациональные уравнения (неравенства). Метод равносильных преобразований для решения иррациональных уравнений (неравенств). Метод следствий для решения иррациональных уравнений.
и её график. Иррациональные уравнения (неравенства). Метод равносильных преобразований для решения иррациональных уравнений (неравенств). Метод следствий для решения иррациональных уравнений.
3. Тригонометрические функции
Радианная мера угла. Связь радианной меры угла с градусной мерой.
Тригонометрические функции: косинус, синус, тангенс, котангенс. Знаки значений тригонометрических функций. Чётность и нечётность тригонометрических функций. Периодичность тригонометрических функций. Свойства тригонометрических функций. Графики тригонометрических функций. Обратные тригонометрические функции. Свойства обратных тригонометрических функций и их графики
Косинус, синус, тангенс, котангенс угла поворота. Основные соотношения между косинусом, синусом, тангенсом и котангенсом одного и того же аргумента. Формулы сложения. Формулы приведения. Формулы двойного и половинного углов. Формулы суммы и разности синусов (косинусов). Формулы преобразования произведения в сумму. Тождественные преобразования выражений, содержащих косинусы, синусы, тангенсы и котангенсы.
4. Тригонометрические уравнения и неравенства
Арккосинус, арксинус, арктангенс, арккотангенс. Простейшие свойства арккосинуса, арксинуса, арктангенса, арккотангенса. Тригонометрические уравнения (неравенства). Основные тригонометрические уравнения (неравенства) и методы их решения. Тригонометрические уравнения, сводящиеся к алгебраическим. Однородные уравнения первой и второй степеней. Решение тригонометрических уравнений методом разложения на множители.
5. Производная и её применение
Предел функции в точке. Непрерывность. Промежутки знакопостоянства непрерывной функции. Непрерывность рациональной функции. Метод интервалов. Задачи, приводящие к понятию производной. Производная функции в точке. Таблица производных. Правила вычисления производных. Механический и геометрический смысл производной. Уравнение касательной к графику функции. Признаки возрастания и убывания функции. Точки экстремума функции. Метод нахождения наибольшего и наименьшего значений функции. Построение графиков функций.
6. Повторение и систематизация учебного материала за курс алгебры 10 класса
3. Календарно-тематическое планирование
| № П/п | Тема урока | Дата |
Повторение алгебры 7 – 9 классов 4 часа |
| Алгебраические выражения. |
|
| Уравнения. Системы уравнений |
|
| Функции. Неравенства. |
|
| Входная контрольная работа |
|
| Глава 1. Повторение и расширение сведений о функции. 14 часов |
| Наибольшее и наименьшее значение функции. Четные и нечетные функции. |
|
| Наибольшее и наименьшее значение функции. Четные и нечетные функции. |
|
| Наибольшее и наименьшее значение функции. Четные и нечетные функции. |
|
| Построение графиков функций с помощью геометрических преобразований. |
|
| Обратная функция |
|
| Обратная функция |
|
| Обратная функция |
|
| Равносильные уравнения и неравенства. |
|
| Равносильные уравнения и неравенства. |
|
| Равносильные уравнения и неравенства. |
|
| Метод интервалов. |
|
| Метод интервалов. |
|
| Метод интервалов. |
|
| Контрольная работа №1 по теме «Повторение и расширение сведений о функции» |
|
| Глава 2. Степенная функция 23 часа |
| Степенная функция с натуральным показателем. |
|
| Степенная функция с целым показателем. |
|
| Степенная функция с целым показателем. |
|
| Определение корня n-ой степени. Функция y=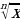 |
|
| Определение корня n-ой степени. Функция y=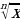 |
|
| Свойства корня n-ой степени. |
|
| Свойства корня n-ой степени. |
|
| Свойства корня n-ой степени. |
|
| Свойства корня n-ой степени. |
|
| Контрольная работа № 2 по теме «Степенная функция. Корень n-ой степени и его свойства» |
|
| Определение и свойства степени с рациональным показателем. |
|
| Определение и свойства степени с рациональным показателем. |
|
| Иррациональные уравнения. |
|
| Иррациональные уравнения. |
|
| Иррациональные уравнения. |
|
| Иррациональные уравнения. |
|
| Метод равносильных преобразований при решении иррациональных уравнений |
|
| Метод равносильных преобразований при решении иррациональных уравнений |
|
| Метод равносильных преобразований при решении иррациональных уравнений |
|
| Иррациональные неравенства. |
|
| Иррациональные неравенства. |
|
| Иррациональные неравенства. |
|
| Контрольная работа №3 по теме «Степень с рациональным показателем и её свойства. Иррациональные уравнения и неравенства» |
|
|
| Глава 3. Тригонометрические функции. 35 часов |
|
| Радианная мера угла. |
|
| Радианная мера угла. |
|
| Тригонометрические функции числового аргумента. |
|
| Тригонометрические функции числового аргумента. |
|
| Знаки значений тригонометрических функций. Четность и нечетность тригонометрических функций. |
|
| Знаки значений тригонометрических функций. Четность и нечетность тригонометрических функций. |
|
| Периодические функции. |
|
| Свойства и графики функций y = sin x, y = cos x |
|
| Свойства и графики функций y = sin x, y = cos x |
|
| Свойства и графики функций y = sin x, y = cos x |
|
| Свойства и графики функций y = tg x, y = ctg x |
|
| Свойства и графики функций y = tg x, y = ctg x |
|
| Свойства и графики функций y = tg x, y = ctg x |
|
| Контрольная работа № 4 по теме «Тригонометрические функции и их свойства» |
|
| Основные отношения между тригонометрическими функциями одного и того же аргумента. |
|
| Основные отношения между тригонометрическими функциями одного и того же аргумента. |
|
| Основные отношения между тригонометрическими функциями одного и того же аргумента. |
|
| Основные отношения между тригонометрическими функциями одного и того же аргумента. |
|
| Формулы сложения. |
|
| Формулы сложения. |
|
| Формулы сложения. |
|
| Формулы приведения. |
|
| Формулы приведения. |
|
| Формулы двойного и половинного углов. |
|
| Формулы двойного и половинного углов. |
|
| Формулы двойного и половинного углов. |
|
| Формулы двойного и половинного углов. |
|
| Формулы двойного и половинного углов. |
|
| Сумма и разность синусов (косинусов ) |
|
| Сумма и разность синусов (косинусов ) |
|
| Сумма и разность синусов (косинусов ) |
|
| Формула преобразования произведения тригонометрических функций в сумму. |
|
| Формула преобразования произведения тригонометрических функций в сумму. |
|
| Формула преобразования произведения тригонометрических функций в сумму. |
|
| Контрольная работа № 5 «Соотношение между тригонометрическими функциями одного и того же аргумента. Формулы сложения и их следствия» |
|
|
| Глава 4. Тригонометрические уравнения и неравенства. 22 часа |
|
| Уравнение cos x = b |
|
| Уравнение cos x = b |
|
| Уравнение cos x = b |
|
| Уравнение sin x = b |
|
| Уравнение sin x = b |
|
| Уравнение sin x = b |
|
| Уравнение tg x = b, ctg x = b |
|
| Уравнение tg x = b, ctg x = b |
|
| Уравнение tg x = b, ctg x = b |
|
| Функции y= arcos x, y = arcsin x, y = arctg x, y = arcctg x |
|
| Функции y= arcos x, y = arcsin x, y = arctg x, y = arcctg x |
|
| Функции y= arcos x, y = arcsin x, y = arctg x, y = arcctg x |
|
| Тригонометрические уравнения, сводящиеся к алгебраическим. |
|
| Тригонометрические уравнения, сводящиеся к алгебраическим. |
|
| Тригонометрические уравнения, сводящиеся к алгебраическим. |
|
| Решение тригонометрических уравнений методом разложения на множители. |
|
| Решение тригонометрических уравнений методом разложения на множители. |
|
| Решение тригонометрических уравнений методом разложения на множители. |
|
| Решение простейших тригонометрических неравенств. |
|
| Решение простейших тригонометрических неравенств. |
|
| Решение простейших тригонометрических неравенств. |
|
| Контрольная работа № 6 по теме «Тригонометрические уравнения и неравенства» |
|
|
| Глава 5. Производная и её применение 32 часа |
|
| Представление о пределе функции в точке и о непрерывности функции в точке |
|
| Представление о пределе функции в точке и о непрерывности функции в точке |
|
| Представление о пределе функции в точке и о непрерывности функции в точке |
|
| Задачи о мгновенной скорости и касательной к графику функции |
|
| Понятие производной |
|
| Понятие производной |
|
| Понятие производной |
|
| Правила вычисления производных |
|
| Правила вычисления производных |
|
| Правила вычисления производных |
|
| Уравнение касательной |
|
| Уравнение касательной |
|
| Уравнение касательной |
|
| Уравнение касательной |
|
| Контрольная работа № 7 «Производная. Уравнение касательной» |
|
| Признаки возрастания и убывания функции |
|
| Признаки возрастания и убывания функции |
|
| Признаки возрастания и убывания функции |
|
| Точки экстремума функции |
|
| Точки экстремума функции |
|
| Точки экстремума функции |
|
| Точки экстремума функции |
|
| Применение производной при нахождении наибольшего и наименьшего значений функции |
|
| Применение производной при нахождении наибольшего и наименьшего значений функции |
|
| Применение производной при нахождении наибольшего и наименьшего значений функции |
|
| Применение производной при нахождении наибольшего и наименьшего значений функции |
|
| Построение графиков функций |
|
| Построение графиков функций |
|
| Построение графиков функций |
|
| Построение графиков функций |
|
| Построение графиков функций |
|
| Контрольная работа № 8 «Применение производной» |
|
|
Повторение курса Алгебры и НМА 10 класса, 6 часов |
| 131-133 | Обобщение по пройденному материалу | 3 |
| 134-135 | Итоговая контрольная работа | 2 |
| 136 | Анализ контрольной работы | 1 |







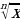 , степенных, тригонометрических, обратных тригонометрических, показательных и логарифмических функций;
, степенных, тригонометрических, обратных тригонометрических, показательных и логарифмических функций;









