

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока


Рабочая программа по геометрии 7-9 класс
Просмотр содержимого документа
«Рабочая программа по геометрии 7-9 класс»
Пояснительная записка
Рабочая программа составлена к УМК Л.А. Атанасян и др. « Геометрия 7-9" на основе федерального компонента государственного стандарта общего образования, утвержденного приказом Министерства образования и науки РФ от 17.12.2010 г. №1897 с изменениями, программы для общеобразовательных учреждений по геометрии 7–9 классы, к учебному комплексу для 7-9 классов (авторы Л.С. Атанасян, В.Ф. Бутузов, С.В. Кадомцев и др., составитель Т.А. Бурмистрова – М: «Просвещение», 2016), ООП ООО МБОУ «Степная СОШ»,учебного плана МБОУ «Степная СОШ» , положения о рабочей программе МБОУ " Степная СОШ"
Геометрия 7 - 9: Учеб.для общеобразоват. учреждений/ JI.C. Атансян,В.Ф.Бутузов, С.Б. Кадомцев и др. -2-е изд.- М.: Просвещение, 2017-383 с.
Н.Б.Мельникова.Г.БЛудина, Н.М.Лепихова. Геометрия. Дидактические материалы для 7-9 классов. - М.: Мнемозина, 2017.
С.М. Саакян. В.Ф. Бутузов. Изучение геометрии в 7-9 классах: Методические рекомендации к учебнику. Книга для учителя. - М.: Просвещение, 2016.
Тесты по геометрии: 7 класс: к учебнику Л.С. Атанасяна и др. «Геометрия 7 – 9 классы» / А.В. Фарков. – М.: Издательство «Экзамен», 2016
Основные цели курса:
1) в направлении личностного развития
развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;
формирование у уч-ся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
• воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
• формирование качеств мышления, необходимых для адаптации в современном информационном обществе;
• развитие интереса к математическому творчеству и математических способностей;
2) в метапредметном направлении
• формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;
• развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
• формирование способов интеллектуальной деят-ти, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деят-ти;
3) в предметном направлении
• овладение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных учреждениях, изучения смежных дисциплин, применения в повседневной жизни;
• создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.
Задачи обучения:
-ввести основные геометрические понятия, научить различать их взаимное расположение;
-научить распознавать геометрические фигуры и изображать их;
-ввести понятия: теорема, доказательство, признак, свойство;
-изучить все о треугольниках (элементы, признаки равенства);
-изучить признаки параллельности прямых и научить применять их при решении задач и доказательстве теорем;
-научить решать геометрические задачи на доказательства и вычисления;
-подготовить к дальнейшему изучению геометрии в последующих классах.
Место предмета в учебном плане.
Согласно базисному учебному плану для образовательных учреждений рабочая программа в 7 и 8 классах рассчитана на 70 часов(2 ч в неделю) в каждом классе, в 9 классах- на 68часов (2 ч в неделю).В рабочую программу внесены изменения: в 7 классе на изучение геометрии отводится 50 часов(II, III ,IV- четверти по 2часа в неделю)
Планируемые результаты изучения курса геометрии в 7-9 классах.
Наглядная геометрия
Выпускник научится:
1) распознавать на чертежах, рисунках, моделях и в окружающем мире плоские и пространственные геометрические фигуры;
2) распознавать развертки куба, прямоугольного параллелепипеда, правильной пирамиды, цилиндра и конуса;
3) определять по линейным размерам развертки фигуры линейные размеры самой фигуры и наоборот;
4) вычислять объем прямоугольного параллелепипеда;
Выпускник получит возможность:
5) вычислять объемы пространственных геометрических фигур, составленных их прямоугольных параллелепипедов;
6) применять понятие развертки для выполнения практических расчетов.
Геометрические фигуры
Выпускник научится:
1) пользоваться языком геометрии для описания предметов окружающего мира и их взаимного расположения;
2) распознавать и изображать на чертежах и рисунках геометрические фигуры;
3) находить значения длин линейных элементов фигур и их отношения, градусную меру углов от 00 до 1800, применяя определения, св-ва и признаки фигур и их элементов, отношения фигур (равенство, подобие, симметрии, поворота, параллельный перенос);
4) оперировать с начальными понятиями тригонометрии и выполнять элементарные операции над функциями углов;
5) решать задачи на доказательство, опираясь на изученные св-ва фигур и отношений между ними и применяя изученные методы доказательств;
6) решать несложные задачи на построение, применяя основные алгоритмы построения с помощью циркуля и линейки;
7) решать простейшие планиметрические задачи в пространстве.
Измерение геометрических величин
Выпускник научится:
1)использовать свойства измерения длин, площадей и углов при решении задач на нахождение длины отрезка, длины окружности, длины дуги окружности, градусной меры угла;
2)вычислять длины линейных элементов фигур и их углы, используя формулы длины окружности и длины дуги окружности, формулы площадей фигур;
3)вычислять площади треугольников, прямоугольников, параллелограммов, трапеций, кругов и секторов;
4)вычислять длину окружности, длину дуги окружности;
5)решать задачи на док-во с использованием формул длины окружности и длины дуги окружности, формул площадей фигур;
6)решать задачи, связанные с нахождением геометрических величин (используя при необходимости справочники и технические средства);
Координаты
Выпускник научится:
1) вычислять длину отрезка по координатам его концов; вычислять координаты середины отрезка;
2) использовать координатный метод для изучения св-ств прямых и окружностей;
Векторы
Выпускник научится:
1) оперировать с векторами: находить сумму и разность двух векторов, заданных геометрически, находить вектор, равный произведению заданного вектора на число;
2) находить для векторов, заданных координатами: длину вектора, координаты суммы и разности двух и более векторов, координаты произведения вектора на число;
3) вычислять скалярное произведение векторов, находить угол между векторами, устанавливать перпендикулярность прямых.
Личностные, метапредметные и предметные результаты освоения содержания курса
Программа обеспечивает достижение следующих результатов освоения образовательной
программы основного общего образования:
личностные:
формирование ответственного отношения к учению, готовности и способности обуч-хся к саморазвитию и самообразованию на основе мотивации к обучению и по знанию, выбору дальнейшего образования на базе ориентировки в мире профессий, осознанному построению индивидуальной образовательной траектории с учётом устойчивых познавательных интересов;
формирование целостного мировоззрения, соответствующего современному уровню развития науки;
формирование коммуникативной компетентности в общении и сотрудничестве в образовательной, общественно полезной, учебно - исследовательской, творческой и других видах деят-ти;
умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, приводить примеры и контрпримеры;
критичность мышления, умение отличать гипотезу от факта;
креативность мышления, инициатива, находчивость, активность при решении геометрических задач;
умение контролировать процесс и результат учебной математической деят-ти;
метапредметные:
умение самост-но планировать альтернативные пути достижения целей, выбирать наиболее эффективные способы решения учебных и познавательных задач;
умение осуществлять контроль по результату действия на уровне произвольного внимания и вносить необходимые коррективы;
умение устанавливать причинно -следственные связи, строить логическое рассуждение, умозаключение и выводы;
умение создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач;
умение организовывать учебное сотрудничество и совместную деят-ть с учителем и сверстниками: определять цели, распределять функции и роли участников, общие способы работы; умение работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов; формулировать, аргументировать и отстаивать своё мнение;
формирование и развитие учебной компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентности);
умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
умение находить инф-ию, необходимую для решения математических проблем, и представлять её в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной инф-ии;
умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
умение самост-но ставить цели, выбирать и создавать алгоритмы для решения учебных мат-ких проблем;
умение планировать и осуществлять дея-ть, направленную на решение задач исследовательского хар-ра; предметные:
овладение базовым понятийным аппаратом по основным разделам содержания; представление об основных изучаемых понятиях (число, геометрическая фигура) как важнейших мат-их моделях, позволяющих описывать и изучать реальные процессы и явления;
умение работать с геометрическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, проводить классификации, логические обоснования, доказательства математических утверждений;
овладение навыками устных, письменных, инструментальных вычислений;
овладение геометрическим языком, умение использовать его для описания предметов окружающего мира, развитие пространственных представлений и изобразительных умений, приобретение навыков геометрических построений;
усвоение знаний о плоских фигурах и их св-ах, а также на наглядном уровне — о простейших пространственных телах, умение применять знания о них для решения геометрических и практических задач;
умение измерять длины отрезков, величины углов, использовать формулы для нахождения периметров, площадей и объёмов геометрических фигур;
умение применять изученные понятия, рез-ты, методы для решения задач практического хар-ра и задач из смежных дисциплин с использованием при необходимости справочных материалов, калькулятора, компьютера.
Учебно- тематический план
7 класс
| № главы | Тема раздела (модуль) | Кол-во часов |
| I | Начальные геометрические сведения | 7 |
| II | Треугольники | 14 |
| III | Параллельные прямые | 9 |
| IV. | Соотношения между сторонами и углами треугольника | 16 |
|
| Повторение. Решение задач | 4 |
|
| Итого | 50 |
8 класс
| № главы | Тема раздела (модуль ) | Кол-во часов |
|
|
|
|
| V | Четырехугольники | 14 |
| VI | Площадь | 14 |
| VII | Подобные треугольники | 19 |
| VIII | Окружность | 17 |
|
| Повторение | 6 |
|
| Итого | 70 |
9 класс
| № главы | Тема раздела (модуль ) | Кол-во часов |
|
|
|
|
| IX | Векторы. | 12 |
| X | Метод координат | 10 |
| XI | Соотношения между сторонами и углами треугольника. Скалярное произведение векторов. | 17 |
| XII | Длина окружности и площадь круга. | 11 |
| XIII. | Движения. | 7 |
| XIV | Начальные сведения из стереометрии | 9
|
|
| Об аксиомах планиметрии | |
|
| Повторение. Решение задач. | 2 |
|
| Итого | 68 |
СОДЕРЖАНИЕ УЧЕБНОГО ПРЕДМЕТА
7класс.
Глава 1.Начальные геометрические сведения (7 часов)
Прямая и отрезок. Луч и угол. Сравнение отрезков и углов. Измерение отрезков. Измерение углов. Перпендикулярные прямые. Решение задач.
Глава 2. Треугольники (14 часов)
Первый признак равенства треугольников. Медианы, биссектрисы и высоты треугольника. Второй и третий признаки равенства треугольников. Задачи на построение. Решение задач.
Глава 3. Параллельные прямые (9 часов)
Признаки параллельности двух прямых. Аксиома параллельности прямых. Решение задач.
Глава 4. Соотношения между сторонами и углами треугольника (16 часов)
Сумма углов треугольника. Теорема о соотношениях между сторонами и углами треугольника. Некоторые свойства прямоугольных треугольников. Построение треугольника по трем элементам.
Повторение. Решение задач. (4 часа)
8 класс.
Глава 5.Четырехугольники (14 часов)
Многоугольник. Параллелограмм и трапеция. Прямоугольник, ромб, квадрат. Решение задач.
Глава 6.Площадь (14 часов)
Понятие площади многоугольника. Площади прямоугольника, параллелограмма, треугольника, трапеции. Теорема Пифагора.
Глава7. Подобные треугольники (19 часов)
Подобные треугольники. Признаки подобия треугольников. Применение подобия к доказательству теорем и решению задач. Синус, косинус и тангенс острого угла прямоугольного треугольника.
Глава 8. Окружность (17 часов)
Взаимное расположение прямой и окружности. Касательная к окружности, ее свойство и признак. Центральные и вписанные углы. Четыре замечательные точки треугольника. Вписанная и описанная окружности.
Повторение. Решение задач. (6 часов)
9 класс.
Глава 9. Векторы. (12 часов)
Понятие вектора. Равенство векторов. Сложение и вычитание векторов. Умножение вектора на число. Разложение вектора по двум неколлинеарным векторам.
Глава 10. Метод координат. (10 часов)
Координаты вектора. Простейшие задачи в координатах. Уравнения окружности и прямой. Применение векторов и координат при решении задач.
Глава 11. Соотношения между сторонами и углами треугольника. Скалярное произведение векторов. (17 часов)
Синус, косинус и тангенс угла. Теоремы синусов и косинусов. Решение треугольников. Скалярное произведение векторов и его применение в геометрических задачах.
Глава 12. Длина окружности и площадь круга. (11 часов)
Правильные многоугольники. Окружности, описанная около правильного многоугольника и вписанная в него. Построение правильных многоугольников. Длина окружности. Площадь круга.
Глава 13. Движения. (7часов)
Отображение плоскости на себя. Понятие движения. Осевая и центральная симметрии. Параллельный перенос. Поворот. Наложения и движения.
Глава 14. Начальные сведения из стереометрии. (7 часов)
Предмет стереометрии. Призма. Параллелепипед. Пирамида. Цилиндр.
Об аксиомах геометрии. (2 часа)
Беседа об аксиомах геометрии.
Повторение. Решение задач. (2часа)
Повторение, обобщение и систематизация знаний, умений и навыков за курс геометрии 9 класса. Подготовка к экзамену..
Требования к уровню подготовки учащихся 7 класса
Должны знать/понимать: определение точки, прямой. отрезка, луча, угла; ед-цы измерения отрезка, угла, определение вертикальных и смежных углов, их свойства; определение перпендикулярных прямых; определение треуг-ка, виды треугольников, признаки равенства треуг-ов, св-ва равнобедренного треугольника, определение медианы, биссектрисы, высоты; определение параллельных прямых, их свойства и признаки; соотношение между сторонами и углами треуг-ка, теорему о сумме углов треуг-ка; определение прямоугольного треуг-ка, его свойства и признаки.
Должны уметь: обозначать точки, отрезки и прямые на рисунке, сравнивать отрезки и углы, с помощью транспортира проводить биссектрису угла; изображать прямой, острый, тупой и развернутый углы; изображать треугольники и находить их периметр; строить биссектрису, высоту и медиану треугольника; доказывать признаки равенства треугольников; показывать на рисунке пары накрест лежащих, соответственных, односторонних углов, доказывать признаки параллельности двух прямых; доказывать теорему о сумме углов треугольника; знать , какой угол называется внешним углом треугольника; применять признаки прямоугольных треугольников к решению задач; строить треугольники по трем элементам.
Должны владеть компетенциями: познавательной, коммуникативной, информационной и рефлексивной.
Способы решать следующие жизненно-практические задачи: самостоятельно приобретать и применять знания в различных ситуациях, работать в группах, аргументировать и отстаивать свою точку зрения, уметь слушать других, извлекать учебную информацию на основе сопоставительного анализа объектов, пользоваться предметным указателем, энциклопедией и справочником для нахождения информации, самостоятельно действовать в ситуациях неопределенности при решении актуальных для них проблем.
Требования к уровню подготовки учащихся 8 класса Должны знать/понимать:
Начальные понятия и теоремы геометрии.
Многоуг-ки. окружность и круг. Наглядные представления о пространственных телах: кубе, параллелепипеде, призме, пирамиде, шаре, сфере, конусе, цилиндре. Примеры сечений. Примеры разверток.
Треуг-ик. теорема Фалеса. Подобие треуг-ов; коэффициент подобия. Признаки подобия треуг-ов.
Теорема Пифагора. Признаки равенства прямоугольных треугольников. Синус, косинус, тангенс и котангенс острого угла прямоугольного треугольника и углов от 0 до 180 ; приведение к острому углу.
Замечательные точки треуг-ка: точки пересечения серединных перпендикуляров, биссектрис, медиан.
Четырехугольник. Параллелограмм, его свойства и признаки. Прямоугольник, квадрат, ромб, их свойства и признаки. Трапеция, равнобедренная трапеция.
Многоугольники. Выпуклые многоугольники. Сумма углов выпуклого многоугольника. Вписанные и описанные многоугольники. Правильные многоугольники.
Окружность и круг. Центр, радиус, диаметр. Дуга, хорда. Центральный, вписанный угол; величина вписанного угла. Взаимное расположение прямой и окружности, двух окружностей. Касательная и секущая к окружности, равенство касательных, проведенных из одной точки. Метрические соотношения в окружности: свойства секущих, касательных, хорд.
Окружность, вписанная в треугольник, и окружность, описанная около треугольника. Вписанные и описанные четырехугольники. Вписанные и описанные окружности правильного многоугольника.
Измерение геометрических величин. Длина ломаной, периметр прямоугольника. Понятие о площади плоских фигур. Равносоставленные и равновеликие фигуры. Площадь прямоугольника. Площадь параллелограмма, треугольника и трапеции.Связь между площадями подобных фигур.
Геометрические преобразования. Симметрия фигур. Осевая и центральная симметрии. Должны уметь: пользоваться геометрическим языком для описания предметов окружающего мира; распознавать геометрические фигуры, различать их взаимное расположение; изображать геометрические фигуры, выполнять чертежи по условию задачи; осуществлять преобразования фигур. Вычислять значения геометр-их величин (длин, углов, площадей); определять значения тригонометр-их ф-ий по заданным значениям углов; находить стороны, углы и пл-ди треуг-ов, длины дуг окружности, площадей основных геометр-их фигур и фигур, составленных из них.
Решать геометрические задачи, опираясь на изученные св-ва фигур и отношений между ними, применяя дополнительные построения, алгебраический аппарат, соображения симметрии. Проводить доказательные рассуждения при решении задач, используя известные теоремы. Решать простейшие планиметрические задачи в пространстве.
Должны владеть компетенциями: учебно-познавательной, рефлексивной, коммуникативной, информационной, социально-трудовой.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни: для описания реальных ситуаций на языке геометрии; расчетов, включающих простейшие тригонометрические формулы; решения геометрических задач с использованием тригонометрии. Решения практических задач, связанных с нахождением геометрических величин; построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).
Требования к уровню подготовки учащихся 9 класса Должны знать/понимать:
Следующие понятия : вектор, сумма и разность векторов; произведение вектора на число, скалярное произведение векторов; синус, косинус, тангенс, котангенс; теорема синусов и косинусов; решение треугольников; соотношение между сторонами и углами треугольника. Определение многоугольника; формулы длины окружности, площади круга; свойства вписанной и описанной окружности около правильного многоугольника; понятие движения на плоскости: симметрия, параллельный перенос, поворот.
Должны уметь: пользоваться геометрическим языком для описания предметов окружающего мира; распознавать геометрические фигуры, различать их взаимное расположение; изображать геометрические фигуры; выполнять чертежи по условию задачи. Распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их; в простейших случаях строить сечения и развертки пространственных тел. Проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами. Вычислять значения геометрических величин (длин, углов, площадей, объемов); находить стороны, углы и площади треугольников, длины дуг окружности, площадей основных геометрических фигур и фигур, составленных из них. решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, симметрию. Проводить доказательные рассуждения при решении задач, используя известные теоремы; решать простейшие планиметрические задачи в пространстве.
Должны владеть компетенциями:
информационной;коммуникативной;
математической, подразумевающей, что уч-ся умеют использовать математические знания, для описания и решения проблем реальной жизни, грамотно пользоваться математическими формулами , применять приобретенные алгебраические преобразования и функционально-графические представления для описания и анализа закономерностей, существующих в окружающем мире и в смежных предметах;
социально-личностной, подразумевающей, что уч-ся владеют стилем мышления, характерным для математики, доказательностью, умеют приводить аргументированные рассуждения, делать логические обоснованные выводы, проводить обобщения, выдвигать гипотезы, ясно и точно выражать свои мысли в устной и письменной речи;
предметно-мировоззренческой, подразумевающей, что уч-ся понимают законы математической логики, владеют приемами построения и исследования моделей при решении прикладных задач.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни: для описания реальных ситуаций на языке геометрии; для расчетов, включающих простейшие тригонометрические формулы; при решении геометрических задач с использованием тригонометрии; для решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства); при построении геометрическими инструментами (линейка, угольник, циркуль, транспортир).
Содержание
| Разделы программы (часы) | Темы входящие в данный раздел | Кол-во часов | Основные виды деятельности обучающихся (на уровне универсальных учебных действий) |
| 7 класс | |||
| Начальные геометрические сведения (7 часов)
| Прямая и отрезок. Луч и угол. Сравнение отрезков и углов. Измерение отрезков. Измерение углов. Перпендикулярные прямые. К. работа №1 | 1
1
1 1 2 1 | Объяснять, что такое отрезок, луч, угол, какие фигуры называются равными, как сравниваются и измеряются отрезки и углы, что такое градус и градусная мера угла, какой угол называется прямым, тупым, острым, развёрнутым, что такое середина отрезка и биссектриса угла, какие углы называются смежными и какие вертикальными; формулировать и обосновывать утверждения о свойствах смежных и вертикальных углов; объяснять, какие прямые называются перпендикулярными; формулировать и обосновывать утверждение о свойстве двух прямых, перпендикулярных к третьей; изображать и распознавать указанные простейшие фигуры на чертежах; решать задачи, связанные с этими простейшими фигурами. |
| Треугольники (14 часов)
| Первый признак равенства треугольников. Медианы, биссектрисы и высоты треугольника. Второй и третий признаки равенства треугольников. Задачи на построение. Решение задач. К. работа №2
| 2
2
4
3 2 1 | Объяснять, какая фигура называется треугольником, что такое вершины, стороны, углы и периметр треугольника, какой треугольник называется равнобедренным и какой равносторонним, какие треугольники называются равными; изображать и распознавать на чертежах треугольники и их элементы; формулировать и доказывать теоремы о признаках равенства треугольников; объяснять, что называется перпендикуляром, проведённым из данной точки к данной прямой; формулировать и доказывать теорему о перпендикуляре к прямой; объяснять, какие отрезки называются медианой, биссектрисой и высотой треугольника; формулировать и доказывать теоремы о свойствах равнобедренного треугольника; решать задачи, связанные с признаками равенства треугольников и свойствами равнобедренного треугольника; 'формулировать определение окружности; объяснять, что такое центр, радиус, хорда и диаметр окружности; решать простейшие задачи на построение (построение угла, равного данному, построение биссектрисы угла, построение перпендикулярных прямых, построение середины отрезка) и более сложные задачи, использующие указанные простейшие; сопоставлять полученный результат с условием задачи; анализировать возможные случаи. |
| Параллельные прямые (9 часов)
| Признаки параллельности двух прямых. Аксиома параллельности прямых. Решение задач. К. работа №3 | 2 2
4 1 | Формулировать определение параллельных прямых; объяснять с помощью рисунка, какие углы, образованные при пересечении двух прямых секущей, называются накрест лежащими, какие односторонними и какие соответственными; формулировать и доказывать теоремы,выражающие признаки параллельности двух прямых; объяснять, что такое аксиомы геометрии и какие аксиомы уже использовались ранее; формулировать аксиому параллельных прямых и выводить следствия из неё; формулировать и доказывать теоремы о свойствах параллельных прямых, обратные теоремам о признаках параллельности, связанных с накрест лежащими, соответственными и односторонними углами, в связи с этим объяснять, что такое условие и заключение теоремы, какая теорема называется обратной по отношению к данной теореме; объяснять, в чём заключается метод доказательства от противного: формулировать и доказывать теоремы об углах с соответственно параллельными и перпендикулярными сторонами; приводить примеры использования этого метода; решать задачи на вычисление, доказательство и построение, связанные с параллельными прямыми. |
| Соотношения между сторонами и углами треугольника (16 часов)
| Сумма углов треугольника. Теорема о соотношениях между сторонами и углами треугольника. К. работа №4 Некоторые свойства прямоугольных треугольников. Построение треугольника по трем элементам. Решение задач. К. работа №5
| 2
3
1 3
3
3 1 | Формулировать и доказывать теорему о сумме углов треугольника и её следствие о внешнем угле треугольника, проводить классификацию треугольников по углам; формулировать и доказывать теорему о соотношениях между сторонами и углами треуг-ка (прямое и обратное утверждения) и следствия из неё, теорему о неравенстве треуг-ка; формулировать и доказывать теоремы о свойствах прямоугольных треуг-ников (прямоугольный треугольник с углом 30°, признаки равенства прямоугольных треугольников); формулировать определения расстояния от точки до прямой, расстояния между параллельными прямыми; решать задачи на вычисления, доказательство и построение, связанные с соотношениями между сторонами и углами треугольника и расстоянием между параллельными прямыми, при необходимости проводить по ходу решения дополнительные построения, сопоставлять полученный результат с условием задачи, в задачах на построение исследовать возможные случаи. |
| Повт. Решение задач. (4часа) |
| 4 |
|
| 8 класс | |||
| Четырехугольники (14 часов) | Многоугольник. Параллелограмм и трапеция. Прямоугольник, ромб, квадрат. Решение задач. К. работа №1 | 2 6
4 1 1
| Показывать элементы многоугольника, его внутреннюю и внешнюю области; формулировать определение выпуклого многоугольника; изображать и распознавать выпуклые и невыпуклые многоугольники. Формулировать и доказывать утверждение о сумме углов выпуклого многоугольника. Объяснять, какие стороны(вершины) называются противоположными. Формулировать определения параллелограмма, трапеции, равнобедренной и прямоугольной трапеций, прямоугольника, ромба, квадрата; распознавать и изображать эти четырехугольники. Формулировать и доказывать утверждения о свойствах и признаках указанных четырехугольников. Решать задачи на вычисление, доказательство и построение, связанные с этими видами четырехугольников. Объяснять, какие две точки называются симметричными относительно прямой(точки), в каком случае фигура называется симметричной относительно прямой(точки) и что такое ось(центр) симметрии фигуры. Приводить примеры фигур, обладающих осевой(центральной) симметрией, а также приводить примеры осевой и центральной симметрии в окружающей нас обстановке. |
| Площадь (14 часов) | Понятие площади многоугольника. Площади прямоугольника, параллелограмма, треугольника, трапеции. Теорема Пифагора. Решение задач. К. работа №2 | 2
6
3 2 1 | формулировать основные свойства площадей. Выводить формулы площадей параллелограмма, треугольника, трапеции, с помощью формул площадей прямоугольника и квадрата. Формулировать и доказывать теорему об отношении площадей треуг-ов, имеющих по равному углу. Формулировать и доказывать теорему Пифагора и обратную ей. Выводить формулу Герона для площади треуг-ка. Решать задачи на вычисление, док-во и построение, связанные с формулами площадей и теоремой Пифагора. |
| Подобные треугольники (19часов) | Подобные треугольники. Признаки подобия треугольников. К. работа №3 Применение подобия к доказательству теорем и решению задач. Синус, косинус и тангенс острого угла прямоугольного треугольника. К. работа №4 | 2 5
1
6
4
1 | Формулировать определения подобных треуг-ов и коэффициента подобия. Формулировать и доказывать теоремы: об отношении площадей подобных треугольников, о признаках подобия треугольников, о средней линии треугольника, о пересечении медиан треугольника, о пропорциональных отрезках в прямоугольном треугольнике. Объяснять, что такое метод подобия в задачах на построение, и приводить примеры этого метода. Формулировать определения и иллюстрировать понятия синуса, косинуса и тангенса острого угла прямоугольного треугольника. Выводить основное тригонометрическое тождество и значения синуса, косинуса, тангенса углов 30,45,60 градусов. Решать задачи, связанные с подобием треугольников и нахождением неизвестных элементов прямоугольного треугольника. |
| Окружность (17 часов) | Касательная к окружности. Центральные и вписанные углы. Четыре замечательные точки треугольника. Вписанная и описанная окружности. Решение задач. К. работа №5
| 3 4
3
4 2
1 | Формулировать определение касательной к окружности. Формулировать и доказывать теоремы: о св-ве касательной, об отрезках касательных, проведенных из одной точки. Формулировать понятия центрального угла и градусной меры дуги окр-ти. Формулировать и доказывать теоремы: о вписанном угле, о произведении отрезков хорд,. Формулировать и доказывать теоремы, связанные с замечательными точками треугольника: о биссектрисе угла и, как следствие, о пересечении биссектрис треугольника; о серединном перпендикуляре к отрезку и, как следствие, о пересечении серединных перпендикулярах к сторонам треугольника; о пересечении высот треугольника. Формулировать определения окружностей, вписанной в многоугольник и описанной около многоугольника. Формулировать и доказывать теоремы: об окружности, вписанной в треугольник, об окружности, описанной около треугольника, об окружности, описанной около треугольника, о свойстве сторон описанного четырехугольника, о свойстве углов вписанного четырехугольника. Решать задачи на вычисление, доказательство, построение, связанные с окружностью, вписанными и описанными треугольниками и четырехугольниками. |
| Повт. Решение задач. (6часов) |
| 6 | Повт., обобщение и систематизация знаний, умений и навыков за курс геометрии 8 класса. |
| 9класс | |||
| Векторы. (12часов) | Понятие вектора. Сложение и вычитание векторов. Умножение вектора на число. Применение векторов и координат при решении задач. К. работа №1 | 2 4
5
1 | Формулировать определения и иллюстрировать понятия вектора, его длины, коллинеарных и равных векторов. Выполнять построение вектора, равного сумме и разности двух векторов, используя при этом правила треуг-ка и параллелограмма. Применять правило многоуг-ка при нахождении суммы нескольких векторов. Выполнять построение вектора, равного произведению вектора на число. Применять векторы и действия над ними при решении геометрических задач. |
| Метод координат. (10 часов) | Координаты вектора. Простейшие задачи в координатах. Ур-ие окр-ти и прямой. Решение задач. К. работа №2 | 2 2
3 2 1 | Объяснять и иллюстрировать понятия прямоугольной системы координат, координат точки и координат вектора. Выводить и использовать при решении задач формулы координат середины отрезка, длины вектора, расстояния между двумя точками, уравнения окружности и прямой. |
| Соотношения между сторонами и углами треугольника. Скалярное произведение векторов. (17 часов) | Синус, косинус и тангенс угла. Теорема о пл-ди треугольника Теоремы синусов и косинусов. Решение треугольников. Скалярное произведение векторов. Решение задач. К. работа №3
| 3
3
5
3
2 1 | Формулировать и иллюстрировать определения синуса, косинуса и тангенса углов от 0 до 180. Выводить основное тригонометрическое тождество и формулы приведения. Формулировать и доказывать теоремы синусов и косинусов, применять их при решении треугольников. Объяснять как используются тригонометрические формулы в измерительных работах на местности. Формулировать определения угла между векторами и скалярного произведения векторов. Выводить формулу скалярного произведения векторов через координаты векторов. Формулировать и обосновывать утверждение о свойствах скалярного произведения. Использовать скалярное произведение при решении задач. |
| Длина окружности и площадь круга. (11 часов)
| Правильные многоугольники. Длина окружности и площадь круга. Решение задач. К. работа №3
| 3 4 3 1 | Формулировать определение
|
| Движения. (7часов)
| Понятие движения. Параллельный перенос. Поворот. Решение задач. К. работа №4
| 2 3 1
1 | Объяснять, что такое отображение плоскости на себя, и в каком случае оно называется движением плоскости. Объяснять, что такое осевая симметрия, центральная симметрия, параллельный перенос и поворот. Обосновывать, что эти отображения плоскости на себя являются движениями. |
| Об аксиомах геометрии. (2 часа) | Беседа об аксиомах геометрии.
| 2 | В данной теме рассказывается о различных системах аксиом геометрии, в частности о различных способах введения понятия равенства фигур. |
| Начальные сведения из стереометрии. (7 часов) | Многогранники. Тела и поверхности вращения. | 3
4 | Объяснять, что такое многогранник, его грани, ребра, вершины, диагонали. Какой многогр-к называется выпуклы. Что такое n- угольная призма, ее основания, боковые грани и боковые ребра. Какая призма называется прямой, и какая наклонной, что такое высота призмы, какая призма называется параллелепипедом и какой параллелепипед называется прямоугольным. Объяснять, что такое объем многогр-ка. Какой многогр-к называется пирамидой, что такое основание, вершина, боковые грани, боковые ребра, и высота пирамиды. Какая пирамида называется правильной, что такое апофема правильной пирамиды. Знать формулу объема пирамиды. Объяснять, какое тело называется цилиндром. Знать, что такое его ось, высота, основания, радиус, боковая поверхность, образующие, развертка боковой поверхности. Какими формулами выражается объем и площадь боковой поверхности цилиндра. Объяснять, какое тело называется конусом. Знать, что такое его ось, высота, основание, радиус, боковая поверхность, образующие, развертка боковой поверхности. Какими формулами выражается объем и площадь боковой поверхности конуса Объяснять, какая поверхность называется сферой и какое тело называется шаром. Что такое радиус и диаметр сферы(шара). Какими формулами выражаются объем шара и площадь сферы. Изображать и распознавать на рисунках призму, параллелепипед, пирамиду, цилиндр, конус, шар. |
| Повторение. Решение задач. (2часа) |
| 2 | Повт., обобщение и систематизация знаний, умений и навыков за курс геометрии 9 класса. Подготовка к ГИА |
Перечень Интернет ресурсов, цифровые образовательных ресурсов и других электронных информационных источников:
.Цифровые образовательные ресурсы (ЦОР) к учебникам издательства "Мнемозина" представлены на сайте http://school-collection.edu.ru/
www.math.ru. Интернет - поддержка учителей математики, материалы для уроков, официальные документы Министерства образования и науки, необходимые в работе.
www.it-n.ru. Сеть творческих учителей.
www.etudes.ru. Математические этюды. На сайте представлены этюды, выполненные с использованием современной компьютерной 3D-графики, увлекательно и интересно рассказывающие о математике и ее приложениях.
www.problems.ru. База данных задач по всем темам школьной математики. Задачи разбиты по рубрикам и степени сложности. Ко всем задачам приведены решения.
www.golovolomka.hobby.ru. Головоломки для умных людей. На сайте можно найти много задач (логических, на взвешивания и др.), вариации на тему кубика Рубика, электронные версии книг Р. Смаллиана, М. Гарднера, Л. Кэрролла, ведения занятий, приемах работы на уроках.
www.college.ru/mathematics. Математика на портале «Открытый колледж ». Можно найти учебный материал по различным разделам математики.
www.int-edu.ru. Институт новых технологий. На сайте можно ознакомиться с продукцией, предлагаемой Институтом, например, программами «Живая статистика», «АвтоГраф», развивающе-обучающей настольной игрой «Доли и дроби» и др.
school-collection.edu. Единая коллекция цифровых образовательных ресурсов.
http://www.prosv.ru. Сайт издательства «Просвещение» (рубрика «Математика»)
http:/www.drofa.ru. Сайт издательства Дрофа (рубрика «Математика»)
http://www.center.fio.ru/som. Методические рекомендации учителю- предметнику (представлены все школьные предметы). Материалы для самостоятельной разработки профильных проб и активизации процесса обучения в старшей школе.
http://www.edu.ru. Центральный образовательный портал, содержит нормативные документы а.
http://www.legion.ru. Сайт издательства «Легион».
http://www.intellectcentre.ru. Сайт издательства «Интеллект-Центр», где можно найти учебнотренировочные материалы, демонстрационные версии, банк тренировочных заданий с ответами, методические рекомендации и образцы решений
Приложение 1
Нормы оценки знаний, умений и навыков учащихся по математике.
Оценка письменных контрольных работ обучающихся по математике.
Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два - три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущено более одной ошибки или более двух - трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что обучающийся не обладает обя- зательными умениями по данной теме в полной мере.
Оценка устных ответов обучающихся по математике.
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков; отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна - две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если:
удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков: в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа; допущены один - два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных во - просов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к мат-ой подготовке уч-ся» в настоящей программе по математике);
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учи теля;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теорет-го материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях: не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
3.Общая классификация ошибок.
При оценке знаний, умений и навыков уч-ся следует учитывать все ошибки (грубые и негрубые) и недочёты.
Грубыми считаются ошибки: незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения; незнание наименований единиц измерения; неумение выделить в ответе главное; неумение применять знания, алгоритмы для решения задач; неумение делать выводы и обобщения; неумение читать и строить графики; неумение пользоваться первоисточниками, учебником и справочниками; потеря корня или сохранение постороннего корня; отбрасывание без объяснений одного из них; равнозначные им ошибки; вычислительные ошибки, если они не являются опиской; логические ошибки.
К негрубым ошибкам следует отнести: неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными; неточность графика; нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными); нерациональные методы работы со справочной и другой литературой; неумение решать задачи, выполнять задания в общем виде.
Недочетами являются: нерац-ные приемы вычислений и преобразований; небрежное выполнение записей, чертежей, схем, графиков.
Приложение 2
Контрольно – измерительный материал
Контрольные работы – 7 класс
Контрольная работа №1
Начальные геометрические сведения
Вариант 1
1. Три точки В,С и D лежат на одной прямой. Известно, что ВD = 17 см, DС = 25 см. Какой может быть длина отрезка ВС?
2. Сумма вертикальных углов МОЕ и DОС, образованных при пересечении прямых МС и DЕ, равна 204о. Найдите угол МОD.
3. С помощью транспортира начертите угол, равный 78о, и проведите биссектрису смежного с ним угла.
Вариант 2
1. Три точки M, N, K лежат на одной прямой. Известно, что MN = 15 см, NK = 18 см. Какой может быть длина отрезка MK?
2. Сумма вертикальных углов AOB и COD, образованных при пересечении прямых AD и BC, равна 108о. Найдите угол BОD.
3. С помощью транспортира начертите угол, равный 132о, и проведите биссектрису одного из смежных с ним углов.
Контрольная работа №2
Вариант 1
1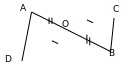 . На рисунке отрезки АВ и СD имеют общую середину О. Докажите, что
. На рисунке отрезки АВ и СD имеют общую середину О. Докажите, что 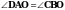 .
.
2. Луч АD – биссектриса угла А. на сторонах угла А отмечены точки В и С так, что 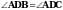 . Докажите, что АВ = АС.
. Докажите, что АВ = АС.
3. Начертите равнобедренный треугольник АВС с основанием ВС. С помощью циркуля и линейки проведите медиану ВВ1 к боковой стороне АС.
Вариант 2
1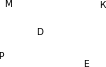 . На рисунке отрезки МЕ и РК точкой D делятся пополам . Докажите, что
. На рисунке отрезки МЕ и РК точкой D делятся пополам . Докажите, что 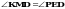 .
.
2.
На сторонах угла D отмечены точки М и К так, что DМ = DК. Точка Р лежит внутри угла D, и РК = РМ. Докажите, что луч DР – биссектриса угла МDК.
3. Начертите равнобедренный треугольник АВС с основанием АС и острым углом В. С помощью циркуля и линейки проведите высоту из вершины угла А.
Контрольная работа №3
Параллельные прямые
Вариант 1
1. Отрезки EF и PQ пересекаются в их середине М. Докажите, что РЕ║QF.
2. Отрезок DM – биссектриса треугольника СDЕ. Через точку М проведена прямая, параллельная стороне СD и пересекающая сторону DЕ в точке N. Найдите углы треугольника DMN, если 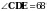 .
.
Вариант 2
1. Отрезки MN и EF пересекаются в их середине Р. Докажите, что ЕN║МF.
2. Отрезок АD – биссектриса треугольника АВС. Через точку D проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F. Найдите углы треугольника АDF, если 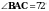 .
.
Контрольная работа №4
Соотношения между сторонами и углами треугольника.
Вариант 1
1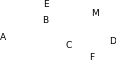 . На рисунке
. На рисунке 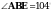 ,
, 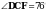 , АC = 12 см. Найдите сторону АВ треугольника АВС.
, АC = 12 см. Найдите сторону АВ треугольника АВС.
2. В треугольнике СDЕ точка М лежит на стороне СЕ, причем угол СМD острый. Докажите, что DЕ DМ.
3. Периметр равнобедренного тупоугольного треугольника равен 45 см, а одна из его сторон больше другой на 9 см. Найдите стороны треугольника.
Вариант 2
1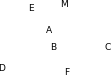 . На рисунке
. На рисунке 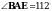 ,
, 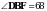 , BC = 9 см. Найдите сторону АC треугольника АВС.
, BC = 9 см. Найдите сторону АC треугольника АВС.
2. В треугольнике MNP точка K лежит на стороне MN, причем угол NKP острый. Докажите, что KPP.
3.Одна из сторон тупоугольного равнобедренного треугольника на 17 см меньше другой. Найдите стороны этого треугольника, если его периметр равен 77 см.
Контрольная работа №5
Прямоугольные треугольники.
Вариант 1
1. В остроугольном треугольнике MNP биссектриса угла М пересекает высоту NK в точке О, причем ОК = 9 см. Найдите расстояние от точки О до прямой МN.
2. Постройте прямоугольный треугольник по гипотенузе и острому углу.
3. С помощью циркуля и линейки постройте угол, равный 150о.
Вариант 2
1. В прямоугольном треугольнике DCEc прямым углом С проведена биссектриса EF, причем FC = 13 см. Найдите расстояние от точки F до прямой DE.
2. Постройте прямоугольный треугольник по катету и прилежащему к нему острому углу.
3. С помощью циркуля и линейки постройте угол, равный 105о.
Итоговая контрольная работа
Вариант 1
1. В равнобедренном треугольнике АВС с основанием АС на медиане ВD отмечена точка К, а на сторонах АВ и ВС – точки М и N соответственно. Известно, что 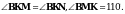
а) Найдите угол BNK.
б) Докажите, что прямые MN и ВК взаимно перпендикулярны.
2. На сторонах АВ, ВС и СА треугольника АВС отмечены точки D, E и F соответственно. Известно, что 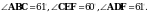
а) Найдите угол DFE.
б) Докажите, что прямые АВ и ЕF пересекаются.
3. В прямоугольном треугольнике АВС катет АВ равен 3 см, угол С равен 150. На катете АС отмечена точка D так, что 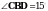 .
.
а) Найдите длину отрезка ВD.
б) Докажите, что ВCcм.
Вариант 2
1. В треугольнике АВС угол А равен 55о. Внутри треугольника отмечена точка О так, что 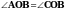 и АО = ОС.
и АО = ОС.
а) Найдите угол АСВ.
б) Докажите, что прямая ВО является серединным перпендикуляром к стороне АС.
2. На прямой последовательно отложены отрезки АВ, ВС и СD.Точки Е и F расположены по разные стороны от этой прямой, причем 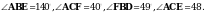
Докажите, что:
а) прямые ВЕ и CF параллельны;
б) прямые ВF и СЕ пересекаются.
3. В треугольнике АВС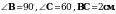 На стороне FС отмечена точка D так, что
На стороне FС отмечена точка D так, что 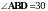 .
.
а) Найдите длину отрезка АD.
б) Докажите, что периметр треугольника АВС меньше 10 см.
Контрольные работы – 8 класс
Контрольная работа №1
Четырехугольники
Вариант 1
1. Диагонали прямоугольника ABCDпересекаются в точке О. Найдите угол между диагоналями, если 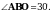
2. В параллелограмме KMNP проведена биссектриса угла MKP, которая пересекает сторону MN в точке Е.
а) Докажите, что треугольник КМЕ равнобедренный.
б) Найдите сторону КР, если МЕ = 10 см, а периметр параллелограмма равен 52 см.
Вариант 2
1. Диагонали ромба КМNP пересекаются в точке О. Найдите углы треугольника КМО, если 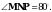
2. На стороне ВС параллелограмма ABCD взята точка M так, что АВ = ВМ.
а) Докажите, что АМ – биссектриса угла ВАD.
б) Найдите периметр параллелограмма, если CD = 8 см, СМ = 4 см.
Контрольная работа №2
Площадь
Вариант 1
1. Смежные стороны параллелограмма равны 32 см и 26 см, а один из его углов равен 150°. Найдите площадь параллелограмма.
2. Площадь прямоугольной трапеции равна 120 см2, а ее высота равна 8 см. Найдите все стороны трапеции, если одно из оснований больше другого на 6 см.
3. Найдите площадь ромба, если его сторона равна 20 см, а диагонали относятся как 3:4.
Вариант 2
1. Одна из диагоналей параллелограмма является его высотой и равна 9 см. Найдите стороны этого параллелограмма, если его площадь равна 108 см2.
2. Найдите площадь трапеции АВСD с основаниями АD и ВС, если АВ = 12 см, ВС = 14 см, АD = 30 см, ![]() В = 150°.
В = 150°.
3. Одна из диагоналей ромба на 4 см больше другой, а площадь ромба равна 96 см2. Найти стороны ромба.
Контрольная работа №3
Подобные треугольники
Вариант 1
1. На рисунке: АВ‖CD.
а) Докажите, чтоА О ОС = ВО OD.
б) Найдите АВ, если ВС = 24 см, ОВ =9 см,CD= 25 см.
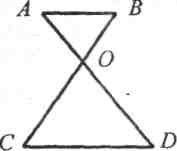
2. Найдите отношение площадей треугольников АВС и KMN, если АВ = 8 см, ВС = 12 см, АС = 16 см, КМ = 10 см, МN = 15 см, NK = 20 см.
Вариант 2
1
В
. На рисунке MN║АС.

М
N
А
а) Докажите, что АВ . BN = CВ .BM.
б) Найдите MN, если AM = 6 см, ВM = 8 см, AС = 21 см.
2. Даны стороны треугольников PQR и АВС: PQ = 16 см, QR = 20 см, PR = 28 см, АВ = 12 см, ВС = 15 см, АС = 21 см. Найдите отношение площадей этих треугольников.
Контрольная работа №4
Соотношения между сторонами и углами в прямоугольном треугольнике
Вариант 1
1. В прямоугольном треугольнике АВС 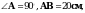 высота АD равна 12 см. Найдите АС и cosC.
высота АD равна 12 см. Найдите АС и cosC.
2. Диагональ ВD параллелограмма АВСD перпендикулярна к стороне АD. Найдите площадь параллелограмма АВСD, если АВ = 12 см, угол А равен 60 градусов.
Вариант 2
1. Высота ВD прямоугольного треугольника АВС равна 24 см и отсекает от гипотенузы АС отрезок DC, равный 18 см. Найдите АВ и cosA.
2. Диагональ АС прямоугольника АВСD равна 3 см и составляет со стороной АD угол 45о. Найдите площадь прямоугольника АВСD.
КОНТРОЛЬНАЯ РАБОТА № 5
Окружность
Вариант I
1. Через точкуА окружности проведены диаметр АС и две хорды АВ и АD, равные радиусу этой окружности. Найдите углы четырехугольника АВСD и градусные меры дуг АВ, ВС, СD, АD.
2. Основание равнобедренного треугольника равно 18 см, а боковая сторона равна 15 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.
Вариант II
1. Отрезок ВD – диаметр окружности с центром О. Хорда АС делит пополам радиус ОВ и перпендикулярна к нему. Найдите углы четырехугольника АВСD и градусные меры дуг АВ, ВС, СD, АD.
2. Высота, проведенная к основанию равнобедренного треугольника, равна 9 см, а само основание равно 24 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.
Итоговая контрольная работа
Вариант 1
1. В трапеции АВСD точка М – середина большего основания АD, МD = ВС, 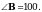 Найдите углы АМС и ВСМ.
Найдите углы АМС и ВСМ.
2. На стороне АD параллелограмма АВСD отмечена точка К так, что АК = 4 см, КD = 5 см, ВК = 12 см. Диагональ ВD равна 13 см.
а) Докажите, что треугольник ВКD прямоугольный.
б) Найдите площади треугольника АВК и параллелограмма АВСD.
3. Отрезки АС и ВD пересекаются в точке О, причем АО = 15 см, ВО = 6 см, СО = 5 см, DO = 18 см. Найдите отношение площадей треугольников АОD и ВОС.
4. Около остроугольного треугольника АВС описана окружность с центром О. Расстояние от точки О до прямой АВ равно 6 см, 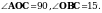 Найдите: а) угол АВО; б) радиус окружности.
Найдите: а) угол АВО; б) радиус окружности.
Вариант 2
1. В трапеции АВСD на большем основании АD отмечена точка М так, что АМ = 3 см, СМ =- 2 см, ,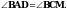 Найдите длины сторон АВ и ВС.
Найдите длины сторон АВ и ВС.
2. В трапеции АВСD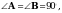 АВ = 8 см, ВC = 4 см, АD = 10 см. Найдите площадь трапеции АВСD.
АВ = 8 см, ВC = 4 см, АD = 10 см. Найдите площадь трапеции АВСD.
3. Через точку М стороны АВ треугольника АВС проведена прямая, перпендикулярная высоте ВD треугольника и пересекающая сторону ВС в точке К. Известно, что ВМ = 7 см, ВК = 9 см, ВС = 27 см. Найдите:
а) длину стороны АВ;
б) отношение площадей треугольников АВС и МВК.
4. В треугольник АВС с прямым углом С вписана окружность с центром О, касающаяся сторон АВ, ВC и СА в точках D, Е и F соответственно. Известно, что 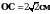 . Найдите: а) радиус окружности; б) угол ЕОF.
. Найдите: а) радиус окружности; б) угол ЕОF.
Геометрия 8 класс. Контрольная работа № 1 по теме: «Четырехугольники»
1 вариант.
Найдите стороны параллелограмма АВСD, если периметр равен 20 см., а сторона АВ меньше ВС на 2 см.?
Найдите углы параллелограмма АСВD, если известно, что угол А меньше угла В в 2 раза?
Найдите углы равнобедренной трапеции, если один из них равен 100º.
Найдите диагональ прямоугольника АВСD, если D = 30º, СD = 4 см.
2 вариант.
Найдите стороны параллелограмма АВСD, если его периметр равен 21 см., а сторона АВ меньше ВС в 2 раза?
Найдите углы параллелограмма АВСD, если известно, что угол А меньше угла В на 20º.
Найдите углы прямоугольной трапеции, если больший из них равен 100º.
Найдите диагональ прямоугольника АВСD, если
Геометрия 8 класс. Контрольная работа № 2 по теме: «Площадь»
1 вариант.
Найдите высоту треугольника, если площадь этого треугольника равна 39,6 дм2, а его основание равно 18 дм.
АВСD – трапеция, АВ и DC – основания, длины которых соответственно равны 19 см и 41 см. АО – высота, АО = 22 см. Найти площадь.
Найти площадь параллелограмма АВСD, если АВ = 15 см, АD = 38 см,
Найти периметр прямоугольника EFKT, еслиKT = 8 см, EK = 17 см
В равнобедренной трапеции АВСD боковая сторона равна 60 мм, а основания равны 90 мм и 18 мм. Найдите высоту трапеции.
В равнобедренном треугольнике АВС, основание АВ = 16 см, боковая сторона 34 см. Найти биссектрису, проведенную к основанию.
2 вариант.
Диагонали ромба равны 16 мм и 24 мм. Найти периметр ромба.
В прямоугольной трапеции АВСD основания равны 17 дм и 40 дм, а высота СD равна 25 дм. Найти площадь.
Найти площадь параллелограмма АВСD, если СВ = 18 см, СD = 5 см,
Найти основание треугольника, если его площадь равна 73,5 дм2, а его высота равна 35 дм.
Найти площадь трапеции АВСD, основания которой 28 см и 46 см, а высота 15 см.
АО – биссектриса в равнобедренном треугольнике АВС равна 36 дм, боковая сторона 45 дм. Найти основание треугольника.
Геометрия 8 класс. Контрольная работа № 3 по теме: «Признаки подобия треугольников»
1 вариант.
∠АСВ=∠СКМ. Найти х 2) Найти FK.
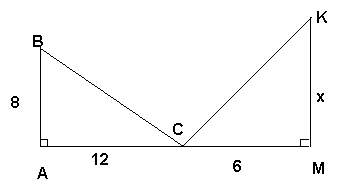
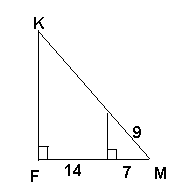
Найти у.
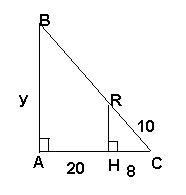
Диагонали трапеции АВСД с основаниями АВ и СД пересекаются в точке О. Найдите АВ, если ОВ=4 см, ОД=10 см, ДС=25 см.
* Докажите, что два равносторонних треугольника подобны.
II-вариант.
∠DAN=∠ARW. Найти RW 2) найти у
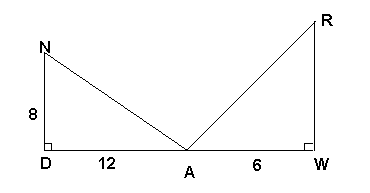
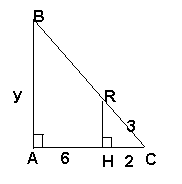
3) Найти FK.

Диагонали трапеции АВСД с основаниями АВ и СД пересекаются в точке О. Найдите АО, если АВ=9,6 дм, ДС=24 см, АС=15 см.
* Докажите, что два равносторонних треугольника подобны.
Геометрия 8 класс. Контрольная работа № 4 по теме: «Применение подобия к решению задач»
1 вариант.
Найти среднюю линий NM треугольника АВС.
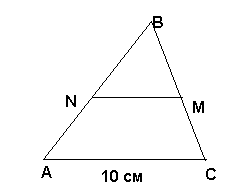
Построить треугольник по данным двум углам и биссектрисе при вершине третьего угла.
Длина тени дерева равна 10 м, а длина тени человека, рост которого 1,8 м равна 3 м. Найти высоту дерева.
Постройте треугольник АВС по двум углам и высоте, проведенной из вершины третьего угла.
Постройте прямоугольный треугольник по гипотенузе и отношению катетов.
II-вариант.
Найти среднюю линий NM треугольника АВС.
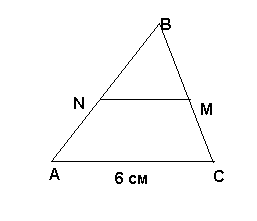
Построить треугольник по данным двум углам и биссектрисе при вершине третьего угла.
Длина тени дерева равна 12 м, а длина тени человека, рост которого 1,6 м равна 2,5 м. Найти высоту дерева.
Постройте треугольник АВС по двум углам и высоте, проведенной из вершины третьего угла.
Постройте прямоугольный треугольник по гипотенузе и отношению катетов.
Геометрия 8 класс. Контрольная работа № 5 по теме: «Окружность»
I-вариант.
Радиус окружности равен 10 см, а расстояние от одного конца диаметра до точки окружности равно 16 см. Найдите расстояние от другого конца диаметра до этой точки.
Из точки А к окружности с центром О проведены касательные АВ и АС (В и С - точки касания). Найдите периметр треугольника АВС, если ОА=12 см, а угол ВОС=600.
Из точки А к окружности с центром О проведена касательная АВ. Найдите АО, если радиус окружности 12, а угол АОВ=450.
Высота, проведенная к основанию равнобедренного треугольника, равно 9см, а само основание равно 24см. Найти радиусы вписанной в треугольник и описанной около треугольника окружностей.
Центр описанной окружности лежит на высоте равнобедренного треугольника и делит высоту на отрезки, равные 5см и 13см. Найти площадь этого треугольника.
II-вариант.
Радиус окружности равен 5 см, а расстояние от одного конца диаметра до точки окружности равно 10 см. Найдите расстояние от другого конца диаметра до этой точки.
Из точки А к окружности с центром О проведены касательные АВ и АС (В и С - точки касания). Найдите периметр треугольника АВС, если ОА=10 см, а угол ВОС=600.
Из точки А к окружности с центром О проведена касательная АВ. Найдите АО, если радиус окружности 12, а угол АОВ=450.
Высота, проведенная к основанию равнобедренного треугольника, равно 9см, а само основание равно 24см. Найти радиусы вписанной в треугольник и описанной около треугольника окружностей.
Основание равнобедренного треугольника равно 18см, а боковая сторона равна 15см. Найти радиусы вписанной в треугольник и описанной около треугольника окружностей.
| Контрольная работа № 1 | |
| 1 вариант.
1). Начертите два неколлинеарных вектора а). 2). На стороне ВС ромба АВСD лежит точкаК такая, что ВК = КС, О – точка пересечения диагоналей. Выразите векторы 3). В равнобедренной трапеции высота делит большее основание на отрезки, равные 5 и 12 см. Найдите среднюю линию трапеции. 4). * В треугольнике АВС О – точка пересечения медиан. Выразите вектор
| 2 вариант
1). Начертите два неколлинеарных вектора а). 2). На стороне СD квадрата АВСD лежит точка Р такая, что СР = РD , О – точка пересечения диагоналей. Выразите векторы 3). В равнобедренной трапеции один из углов равен 600, боковая сторона равна 8 см, а меньшее основание 7 см. Найдите среднюю линию трапеции. 4). * В треугольнике МNK О – точка пересечения медиан, |
| Контрольная работа № 2 | |
| 1 вариант.
1). Найдите координаты и длину вектора 2). Напишите уравнение окружности с центром в точкеА (- 3;2), проходящей через точку В (0; - 2).
3). Треугольник МNK задан координатами своих вершин: М ( - 6; 1 ), N (2; 4 ), К ( 2; - 2 ). а). Докажите, что Δ б). Найдите высоту, проведённую из вершины М.
4). * Найдите координаты точки N, лежащей на оси абсцисс и равноудалённой от точекР и К, если Р( - 1; 3 ) и К( 0; 2 ).
| 2 вариант.
1). Найдите координаты и длину вектора 2). Напишите уравнение окружности с центром в точке С ( 2; 1 ), проходящей через точку D ( 5; 5 ).
3). Треугольник СDЕ задан координатами своих вершин: С ( 2; 2 ), D (6; 5 ), Е ( 5; - 2 ). а). Докажите, что Δ б). Найдите биссектрису, проведённую из вершины С.
4). * Найдите координаты точки А, лежащей на оси ординат и равноудалённой от точекВ и С, если В( 1; - 3 ) и С( 2; 0 ).
|
| Контрольная работа № 3 | |
| 1 вариант
1). В треугольнике АВС
2). Две стороны треугольника равны 7 см и 8 см, а угол между ними равен 1200. Найдите третью сторону треугольника.
3). Определите вид треугольника АВС, если А ( 3;9 ), В ( 0; 6 ), С ( 4; 2 ).
4). * В ΔАВС АВ = ВС,
| 2 вариант
1). В треугольнике СDE
2). Две стороны треугольника равны 5 см и 7 см, а угол между ними равен 600. Найдите третью сторону треугольника.
3). Определите вид треугольника АВС, если А ( 3;9 ), В ( 0; 6 ), С ( 4; 2 ).
4). * В ромбе АВСD АК – биссектриса угла САВ, |
| Контрольная работа № 4 | |
| 1 вариант
1). Найдите площадь круга и длину ограничивающей его окружности, если сторона правильного треугольника, вписанного в него, равна 2). Вычислите длину дуги окружности с радиусом 4 см, если её градусная мера равна 1200. Чему равна площадь соответствующего данной дуге кругового сектора? 3). Периметр правильного треугольника, вписанного в окружность, равен
| 2 вариант
1). Найдите площадь круга и длину ограничивающей его окружности, если сторона квадрата, описанного около него, равна 6 см. 2). Вычислите длину дуги окружности с радиусом 10 см, если её градусная мера равна 1500. Чему равна площадь соответствующего данной дуге кругового сектора? 3). Периметр квадрата, описанного около окружности, равен 16 дм. Найдите периметр правильного пятиугольника, вписанного в эту же окружность.
|
| Контрольная работа № 5 | |
| 1 вариант
1). Начертите ромб АВСD. Постройте образ этого ромба: а). при симметрии относительно точкиС; б).при симметрии относительно прямой АВ; в). При параллельном переносе на вектор г). При повороте вокруг точки D на 600 по часовой стрелке.
2). Докажите, что прямая, содержащая середины двух параллельных хорд окружности, проходит через её центр.
3). * Начертите два параллельных отрезка, длины которых равны.начертите точку, являющуюся центром симметрии, при котором один отрезок отображается на другой.
| 2 вариант
1). Начертите параллелограмм АВСD. Постройте образ этого параллелограмма: а).при симметрии относительно точки D; б).при симметрии относительно прямой CD; в). При параллельном переносе на вектор г). При повороте вокруг точкиА на 450 против часовой стрелки.
2). Докажите, что прямая, содержащая середины противоположных сторон параллелограмма, проходит через точку пересечения его диагоналей.
3).* Начертите два параллельных отрезка, длины которых равны. Постройте центр поворота, при котором один отрезок отображается на другой.
|
30


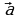 и
и 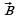 . Постройте векторы, равные:
. Постройте векторы, равные: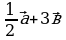 ; б).
; б). 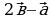
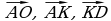 через векторы
через векторы 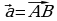 и
и 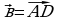 .
.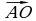 через векторы
через векторы 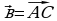 .
.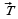 и
и 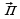 . Постройте векторы, равные:
. Постройте векторы, равные: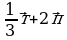 ; б).
; б). 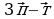
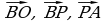 через векторы
через векторы 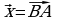 и
и 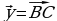 .
.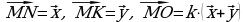 . Найдите число k.
. Найдите число k.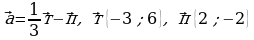 .
.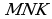 - равнобедренный;
- равнобедренный;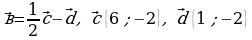 .
.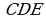 - равнобедренный;
- равнобедренный;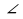 А = 450,
А = 450, 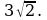 Найдите АС.
Найдите АС.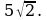 Найдите DE.
Найдите DE.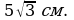
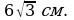 Найдите периметр правильного шестиугольника, описанного около той же окружности.
Найдите периметр правильного шестиугольника, описанного около той же окружности.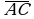 ;
;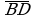 ;
;









