Пояснительная записка
Рабочая программа по геометрии 8 класса составлена на основе:
1.Федеральный закон от 29.12.2012 № 273-ФЗ (ред. От 29.07.2017) «Об образовании в Российской Федерации»;
2.Федеральный государственный стандарт основного общего образования, утвержденного приказом Министерства образования и науки РФ от 17 декабря 2017=0 года № 18979 с послед. Изменениями.
3.Постановление Главного государственного санитарного-эпидемиологические требования к условиям и организации обучения в общеобразовательных учреждениях ( с изменениями)
4.Рекомендации Федеральной службы по надзору в сфере защиты прав потребителей и благополучия человека от 8 мая 2020г № 02/8900-2020-24 « О направлении рекомендаций по организации работы образовательных организаций»
5.Программы общеобразовательных учреждений геометрия 7-9 классы. Составитель Л.С Атанасян.
6.Федеральный перечень учебников, утвержденных, рекомендованных(допущенных) к использованию в образовательном процессе в образовательных учреждениях на 2020-2021 учебный год, реализующих программы общего образования ( с последними изменениями)
7.Основная образовательная программа основного общего образования МАОУ « СОШ № 38 г. Улан-Удэ»
8.Учебный план МАОУ « СОШ № 38 г. Улан-Удэ»
9.Положение о рабочей программе.
Программа рассчитана на 68 часов, 2 часа в неделю.
Цель изучения:
Цели обучения
1.В направлении личностного развития:
Развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;
Формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
Воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
Формирование качеств мышления, необходимых для адаптации в современном информационном обществе;
2.В метапредметном направлении:
Формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;
Развитие представлений о математике как о форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
Формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности.
3.В предметном направлении:
Овладение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных учреждений, изучения смежных дисциплин, применения в повседневной жизни;
Создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.
На протяжении изучения материала предполагается закрепление и отработка основных умений и навыков, их совершенствование, а также систематизация полученных ранее знание, таким образом, решаются следующие задачи:
введение терминологии и отработка умения ее грамотно использования;
развитие навыков изображения планиметрических фигур и простейших геометрических конфигураций;
совершенствование навыков применения свойств геометрических фигур как опоры при решении задач;
формирования умения решения задач на вычисление геометрических величин с применением изученных свойств фигур и формул;
совершенствование навыков решения задач на доказательство;
отработка навыков решения задач на построение с помощью циркуля и линейки;
расширение знаний учащихся о треугольниках, четырёхугольниках и окружности.
Примерная программа конкретизирует содержание предметных тем образовательного стандарта и даёт примерное распределение учебных часов по разделам курса.
Планируемые результаты
В ходе преподавания геометрии в 8 классе, работы над формированием у обучающихся перечисленных в программе знаний и умений следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
ОСНОВНОЕ СОДЕРЖАНИЕ
Четырехугольники (14 часов)
Многоугольник, выпуклый многоугольник, четырехугольник. Параллелограмм, его свойства и признаки. Трапеция. Прямоугольник, ромб, квадрат, их свойства. Осевая и центральная симметрии.
Цель: изучить наиболее важные виды четырехугольников — параллелограмм, прямоугольник, ромб, квадрат, трапецию; дать представление о фигурах, обладающих осевой или центральной симметрией.
Доказательства большинства теорем данной темы и решения многих задач проводятся с помощью признаков равенства треугольников, поэтому полезно их повторить, в начале изучения темы.
Осевая и центральная симметрии вводятся не как преобразование плоскости, а как свойства геометрических фигур, в частности четырехугольников. Рассмотрение этих понятий как движений плоскости состоится в 9 классе.
Площадь (14 часов)
Понятие площади многоугольника. Площади прямоугольника, параллелограмма, треугольника, трапеции. Теорема Пифагора.
Цель: расширить и углубить полученные в 5—6 классах представления обучающихся об измерении и вычислении площадей; вывести формулы площадей прямоугольника, параллелограмма, треугольника, трапеции; доказать одну из главных теорем геометрии — теорему Пифагора.
Вывод формул для вычисления площадей прямоугольника, параллелограмма, треугольника, трапеции основывается на двух основных свойствах площадей, которые принимаются исходя из наглядных представлений, а также на формуле площади квадрата, обоснование которой не является обязательным для обучающихся.
Нетрадиционной для школьного курса является теорема об отношении площадей треугольников, имеющих по равному углу. Она позволяет в дальнейшем дать простое доказательство признаков подобия треугольников. В этом состоит одно из преимуществ, обусловленных ранним введением понятия площади. Доказательство теоремы Пифагора основывается на свойствах площадей и формулах для площадей квадрата и прямоугольника. Доказывается также теорема, обратная теореме Пифагора.
Подобные треугольники (19 часов)
Подобные треугольники. Признаки подобия треугольников. Применение подобия к доказательству теорем и решению задач. Синус, косинус и тангенс острого угла прямоугольного треугольника.
Цель: ввести понятие подобных треугольников; рассмотреть признаки подобия треугольников и их применения; сделать первый шаг в освоении учащимися тригонометрического аппарата геометрии.
Определение подобных треугольников дается не на основе преобразования подобия, а через равенство углов и пропорциональность сходственных сторон.
Признаки подобия треугольников доказываются с помощью теоремы об отношении площадей треугольников, имеющих по равному углу.
На основе признаков подобия доказывается теорема о средней линии треугольника, утверждение о точке пересечения медиан треугольника, а также два утверждения о пропорциональных отрезках в прямоугольном треугольнике. Дается представление о методе подобия в задачах на построение.
В заключение темы вводятся элементы тригонометрии — синус, косинус и тангенс острого угла прямоугольного треугольника.
Окружность (17 часов)
Взаимное расположение прямой и окружности. Касательная к окружности, ее свойство и признак. Центральные и вписанные углы. Четыре замечательные точки треугольника. Вписанная и описанная окружности.
Цель: расширить сведения об окружности, полученные учащимися в 7 классе; изучить новые факты, связанные с окружностью; познакомить обучающихся с четырьмя замечательными точками треугольника.
В данной теме вводится много новых понятий и рассматривается много утверждений, связанных с окружностью. Для их усвоения следует уделить большое внимание решению задач.
Утверждения о точке пересечения биссектрис треугольника и точке пересечения серединных перпендикуляров к сторонам треугольника выводятся как следствия из теорем о свойствах биссектрисы угла и серединного перпендикуляра к отрезку. Теорема о точке пересечения высот треугольника (или их продолжений) доказывается с помощью утверждения о точке пересечения серединных перпендикуляров.
Наряду с теоремами об окружностях, вписанной в треугольник и описанной около него, рассматриваются свойство сторон описанного четырехугольника и свойство углов вписанного четырехугольника.
Решение задач. (4 часа)
Цель: Повторение, обобщение и систематизация знаний, умений и навыков за курс геометрии 8 класса.
При переходе образовательного учреждения на дистанционное обучение по Федеральному закону от 8 июня 2020 г. № 164-ФЗ “О внесении изменений в статьи 71.1 и 108 Федерального закона «Об образовании в Российской Федерации» будут применены следующие онлайн-платформы и средства для учебных коммуникаций.
| Наименование | Ссылки | Классы, предметы | Аннотация |
| Moodle | https://moodle.org/
| Математика 5-9 | система управления знаниями, позволяющая организовать процесс электронного обучения от разработки онлайн курса до его реализации. Свободно распространяется по лицензии GNU GPL
|
| Google Класс
| https://classro om.google.co m/
| Математика 5-11 | Класс – это бесплатный набор инструментов для работы с электронной почтой, документами и хранилищем. Сервис разработан для преподавателей с целью организации занятия.
|
| Российская электронная школа
| http://resh.edu .ru/
| Алгебра (7-9 кл.) Алгебра и начала математического анализа (10-11 кл.) Геометрия (7-11кл.) | «Российская электронная школа» – это полный школьный курс уроков от лучших учителей России; это информационно образовательная среда, объединяющая ученика, учителя, родителя и открывающая равный доступ к качественному общему образованию независимо от социокультурных условий.
|
| Мобильное электронное образование
| https://mobedu.ru/
| Математика 5-6 | МЭО это - создание безопасной образовательной среды; обеспечение условий для организации персонифицированного обучения учащихся в соответствии с их потребностями, а также с запросами региональной экономики; обеспечение доступности качественного образования для различных категорий учащихся, в том числе учащихся с ОВЗ, высокомотивированных и одаренных |
| Учи.ру
| https://uchi.ru/
| Математика 1 – 6кл. Алгебра 7 – 11кл. | Учи.ру — российская онлайн-платформа, где учащиеся из всех регионов России изучают школьные предметы в интерактивной форме. Интерактивные курсы на Учи.ру полностью соответствуют ФГОС. Содержит более 30 000 заданий в игровой форме, разработанных профессиональными методистами и специалистами по детскому интерфейсу. Платформа Учи.ру учитывает скорость и правильность выполнения заданий, количество ошибок и поведение ученика. Для каждого ребенка система автоматически подбирает персональные задания, их последовательность и уровень
|
| Яндекс.Учебник
|
| Математика 5 | Доступно более 35 000 заданий разного уровня сложности. Все задания разработаны опытными методистами с учётом ФГОС НОО. Можно реализовать индивидуальные траектории внутри одного класса. Учитель может назначить задания всему классу или индивидуально, сэкономить время на проверке заданий и подготовке к урокам Задания распределены по темам, и учитель легко ориентируется независимо от того, по какой программе работает. Есть подробная статистика успеваемости |
| Онлайн щкола Фоксфорд
| https://foxford.ru/
| Математика
| Онлайн-подготовка школьников 5 — 11 классов к ЕГЭ, ОГЭ и олимпиадам, а также углубленное изучение школьных предметов в группах и индивидуально
|
| ЯКласс
| http://www.yaklass.ru/ | Алгебра (7-9кл.) Геометрия (7-9кл.) Математика (1-6 кл.)
| Ресурс ориентирован на педагогов, учащихся и родителей. ЯКласс интегрирован с электронными журналами, сотрудничает с популярными издательствами. Содержит 1,6 трлн заданий школьной программы и 1500 видеоуроков. Все материалы соответствуют ФГОС.
|
| Домашняя школа InternetUrok.ru
| https://interneturok.ru/
| Математика 5-11 | Полное среднее образование дистанционно. Для семейного обучения, для тех, кто часто пропускает школу, для проживающих вне России. Возможность официального зачисления в любое время года. Бесплатный доступ открыт.
|
| «Московская электронная школа»
| https://uchebn ik.mos.ru/cata logue | Математика 5-11 | это широкий набор электронных учебников и тестов, интерактивные сценарии уроков в электронной библиотеке. Решения МЭШ доступны для всех и уже получили высокие оценки учителей, родителей и детей ряда. Проверка ошибок, общение с учителями, домашние задания, материалы для подготовки к уроку, варианты контрольных и тестов — всё это доступно родителям, учителям и школьникам с любых устройств. В библиотеку МЭШ
|
| Урок цифры
| https://datalesson.ru/ | Математика 5-11 | «Урок цифры» дает хорошую теоретическую базу и наглядную практическую подготовку в вопросах безопасного использования и развития навыков в онлайн среде. Данные уроки будут полезны и интересны как самим школьникам, так и их родителям |
| Онлайн платформа «Мои достижения»
.
| https://myskills.ru/
| Математика 5-11 | Широкий выбор диагностик для учеников с 1 по 11 класс по школьным предметам и различным тематикам. Материалы для подготовки к диагностикам от Московского центра качества образования |
| Видеоуроки на видеохостинге youtube.com
| https://www.y outube.com
| Математика 5-11 | На видеохостинге youtube.com размещено огромное количество видеоуроков, найти которые можно по названию школьного предмета (ввести название в строку поиска) |
| Видеоуроки.net |
| Математика 5-11 | В этом разделе вы можете эффективно и комфортно проверять знания ваших учеников по различным предметам школьной программы. Больше не надо тратить время на подготовку к практической части урока. С помощью тетради вы легко проведёте практическую часть, закрепите материал и мгновенно проверите решения. |
| Интерактивная тетрадь | Skusmart.ru | Математика 5-11 | Учитель отправляет ученикам
ссылку на задания — прямо на уроке или как домашнюю работу. Они могут заниматься с любого устройства — компьютера, планшета или смартфона. Интерактивная рабочая тетрадь Скайсмарт оценивает выполнение заданий, учитель сразу получает |
|
|
|
| результаты и экономит до 2 часов в день на проверке. Вы видите статистику по всему классу и баллы конкретных учеников |
| Мессенджеры | Skype, Viber, WhatsApp |
| Lkz j,hfnyjq cdzp |
Календарно- тематическое планирование
| № урока
| Название раздела, темы урока | Кол-во часов | дата | Характеристика основных видов деятельности ученика |
Домашнее задание |
| 1 | Вводное повторение | 1 |
| Повторяют наиболее важные вопросы 7 класса. Совершенствует навыки решения задач | Повторить главы 2,№ 22,23.38 |
| 2 | Вводное повторение | 1 |
| Повторяют наиболее важные вопросы 7 класса. Совершенствует навыки решения задач | Задачи по готовым чертежам |
| Глава | Четырехугольники | 14 |
|
|
|
| 3 | Многоугольники | 1 |
| Знакомятся с понятием многоугольника, выпуклого многоугольника, выводят формулу суммы углов многоугольника и учатся находить их | П 40-41-42 №364(а,б)365(а,б,г),368 |
| 4 | Многоугольники | 1 |
| Знакомятся с понятием многоугольника, выпуклого многоугольника, выводят формулу суммы углов многоугольника и учатся находить их | № 366,369,370 |
| 5 | Параллелограмм и трапеция | 1 |
| Знакомятся с понятием параллелограмма и трапеции и их элементами и свойствами и признаками
| П 42 № 371а,372в,376в,г |
| 6 | Параллелограмм и трапеция | 1 |
| Знакомятся с понятием параллелограмма и трапеции и их элементами и свойствами и признаками
| П 44 №383,373,378 |
| 7 | Параллелограмм и трапеция | 1 |
| Знакомятся с понятием параллелограмма и трапеции и их элементами и свойствами и признаками
| № 375,380,384П |
| 8 | Параллелограмм и трапеция | 1 |
| Знакомятся с понятием трапеция и ее элементами, видами трапеции, свойства равнобедренной трапеции | п 45 3386,387,390 |
| 9 | Параллелограмм и трапеция | 1 |
| Рассматривают теорему Фалеса и применяют при решении задач. | №391,392 |
| 10 | Параллелограмм и трапеция | 1 |
| Рассматривают теорему Фалеса и применяют при решении задач | № 396,393,394,398, |
| 11 | Прямоугольник. Ромб. Квадрат | 1 |
| Знакомятся с понятием прямоугольника и его элементами, свойствами прямоугольника | П 45 № 399,401,404 |
| 12 | Прямоугольник. Ромб. Квадрат | 1 |
| Знакомятся с понятием прямоугольника и его элементами, свойствами прямоугольника | П 46 № 405,409.411 |
| 13 | Прямоугольник. Ромб. Квадрат | 1 |
| Знакомятся с ромбом и его свойствами и применяют при решении задач | П 47 № 415,413,410 |
| 14 | Прямоугольник. Ромб. Квадрат | 1 |
| Знакомятся с понятием квадрата и его свойствами ,при меняют при решении задач | Задачи в тетради |
| 15 | Прямоугольник. Ромб. Квадрат | 1 |
| Знакомятся с понятием осевой и центральной симметрии | Задачи по готовым чертежам |
| 16 | Контрольная работа № 1 | 1 |
| Применяют полученные знания по данной теме | Повторить |
| Глава | Площадь | 14 |
|
|
|
| 17 | Площадь многоугольника | 1 |
| Знакомятся с понятием площади многоугольника, рассматривают свойства площадей, выводят формулу для вычисления площади квадрата | П 48,49 № 448 449 450 446 |
| 18 | Площадь прямоугольника | 1 |
| Выводят формулу для вычисления площади прямоугольника. | П 50 № 454 455 456 |
| 19 | Площадь параллелограмма | 1 |
| Выводят формулу для вычисления площади параллелограмма и применяют при нахождении площади данного параллелограмма | П 51 № 459 460 464 462 |
| 20 | Площадь треугольника | 1 |
| Выводят формулу для вычисления площади треугольника и показывают их применение в процессе решения задач. | П 52 № 468 473 469 |
| 21 | Площадь треугольника | 1 |
|
| П 52 №479 476 477 |
| 22 | Площадь трапеции | 1 |
| Выводят формулу для вычисления площади трапеции и их применение при решении задач. | П53 № 480 481 478 476 |
| 23 | Решение задач на вычисление площадей фигур | 1 |
| Решают задачи на вычисление площадей фигур | Дополнительные задачи |
| 24 | Решение задач на нахождение площадей | 1 |
| Решают задачи на вычисление площадей фигур | Дополнительные задачи |
| 25 | Теорема Пифагора | 1 |
| Рассматривают теорему Пифагора, показывают применение данной теоремы при решении задач. | П 54 № 483 484 486 |
| 26 | Теорема, обратная теореме Пифагора | 1 |
| Доказывают теорему, обратную теореме Пифагора. | П55 № 498 499 488 |
| 27 | Решение задач по теме « Теорема Пифагора» | 1 |
| Применяют теорему Пифагора при решении задач | № 489 491 493 |
| 28 | Решение задач по теме « Теорема Пифагора | 1 |
| Применяют теорему Пифагора при решении задач | № 495 494 490 |
| 29 | Решение задач по теме « Теорема Пифагора | 1 |
| Применяют теорему Пифагора при решении задач | № 490 497 503 518 |
| 30 | Контрольная работа №2 по теме « Площадь» | 1 |
| Применяют полученные знания | Повторить |
| Глава | Подобные треугольники | 20 |
|
|
|
| 31 | Определение подобных треугольников | 1 |
| Знакомятся с понятием пропорциональных отрезков и подобных треугольников, свойство биссектрисы треугольника и применяют при решении задач | П 56 57 №534 535 536 538 542 |
| 32 | Отношение площадей подобных треугольников | 1 |
| Рассматривают отношение площадей подобных треугольников и показывают их применение при решении задач | П 58 №544 543 546 549 |
| 33 | Первый признак подобия треугольников | 1 |
| Рассматривают первый признак подобия треугольников их доказательство и применяют данный признак при решении задач. | № 550 551 553 555 |
| 34 | Решение задач на применение первого признака подобия треугольников | 1 |
| Решают задачи с применением первого признака подобия треугольников | П59 №552 557 558 556 |
| 35 | Второй и третий признаки подобия треугольников | 1 |
| Доказывают второй и третий признаки подобия треугольников при решении задач | П 60 61 №559 560 561 |
| 36 | Решение задач на применение признаков подобия | 1 |
| Решают задачи на применение признаков подобия треуольников | №562 563 604 605 |
| 37 | Решение задач на применение признаков подобия | 1 |
| Решают задачи на применение признаков подобия треуольников | Дополнительные задачи |
| 38 | Контрольная работа №3 по теме « Признаки подобия треугольников» | 1 |
| Применяют полученные знания | Повторить |
| 39 | Средняя линия треугольников | 1 |
| Знакомятся и доказывают теорему о средней линии треугольника и учатся решать задачи на нахождение средней линии треугольника | П62 №556 570 571 |
| 40 | Средняя линия треугольников.
| 1 |
| Знакомятся и доказывают теорему о средней линии треугольника и учатся решать задачи на нахождение средней линии треугольника | № 568 569 |
| 41 | Пропорциональные отрезки | 1 |
| Вводят понятие среднего пропорционального двух отрезков, | П63 №572 573 574 |
| 42 | Пропорциональные отрезки в прямоугольном треугольнике | 1 |
| Вводят понятие пропорциональных отрезков в прямоугольном треугольнике, свойств высоты прямоугольного треугольника | №575 577 579 578 |
| 43 | Измерительные работы на местности | 1 |
| Решают задачи на местности, применяя подобия треугольников | П 64 №580 581 |
| 44 | Задачи на построение методом подобия | 1 |
| Решают задачи на построение методом подобия | № 585 587 588 590 |
| 45 | Решение задач на построение методом подобных треугольников | 1 |
| Решают задачи на построение методом подобия | № 606 606 628 629 |
| 46 | Синус, косинус и тангенс острого угла прямоугольного треугольника | 1 |
| Вводят понятие синуса, косинуса, тангенса острого угла в прямоугольном треугольнике, знакомятся с основным тригонометрическим тождеством и применяют при решении задач | П67 591 592 593 |
| 47 | Значения синуса, косинуса и тангенса для углов 30,45 и 60 градусов | 1 |
| Учатся вычислять значения синуса, косинуса и тангенса острых углов в 30,45.60 градусов и применяют при решении задач | П 68№595 597 598 |
| 48 | Соотношения между сторонами и углами прямоугольного треугольника | 1 |
| Учатся решать задачи на нахождении неизвестных элементов в прямоугольном треугольнике | № 559 601 602 |
| 49 | Подготовка к контрольной работе | 1 |
|
| № 620 622 623 625 630 |
| 50 | Контрольная работа № 4 по теме « Применение подобия треугольников» | 1 |
| Применяют полученные знания | Повторить |
| Глава | Окружность | 16 |
|
|
|
| 51 | Взаимное расположение прямой и окружности | 1 |
| Рассматривают различные случаи взаимного расположения прямой и окружности | П 70 № 631 632 633 |
| 52 | Касательная к окружности | 1 |
| Знакомятся с понятием касательной к окружности, точки касания, отрезков касательных, проведенных из одной точки. | П71 № 634 636 639 |
| 53 | Касательная к окружности | 1 |
|
| № 641 643 645 648 |
| 54 | Градусная мера дуги окружности | 1 |
| Знакомятся с градусной мерой дуги окружности, центрального угла, учатся решать задачи на нахождение градусной меры дуги окружности. | П 72 №649 650 651 652 |
| 55 | Теорема о вписанном угле | 1 |
| Знакомятся с понятием вписанного угла, теоремой вписанного угла и их следствиями. | П73 №654 655 657 659 |
| 56 | Теорема об отрезке пересекающихся хорд | 1 |
| Доказывают теорему об отрезках пересекающихся хорд и применяют при решении задач | №666 671 660 668 |
| 57 | Решение задач по теме « Центральные и вписанные углы» | 1 |
|
| № 661 663 672 673 |
| 58 | Свойство биссектрисы угла | 1 |
| Рассматривают свойство биссектрисы угла и применяют при решении задач | № 675 676 678 677 |
| 59 | Серединный перпендикуляр | 1 |
| Вводят понятие серединного перпендикуляра, доказывают теорему о серединном перпендикуляре и их применение при решении задач | № 679 680 681 |
| 60 | Теорема о точке пересечения высот треугольника | 1 |
| Рассматривают доказательство теоремы о точке пересечения высот треугольника и их применение при решении задач | Домашняя проверочная работа |
| 61 | Вписанная окружность | 1 |
| Рассматривают понятие вписанной окружности, доказывают теорему вписанной в треугольник вписанной окружности | № 689 692 693 694 |
| 62 | Свойство описанного четырехугольника | 1 |
| Рассматривают свойство описанного четырехугольника и их применение при решении задач | № 695 699 700 701 |
| 63 | Описанная окружность | 1 |
| Вводят понятие описанной окружности около многоугольника, рассматривают и доказывают теорему об окружности, описанной около треугольника и их применение при решении задач | № 702 705 707 711 |
| 64 | Свойство вписанного четырехугольника | 1 |
| Доказывают свойство вписанного четырехугольника и показывают их применение при решении задач | №708 |
| 65 | Решение задач по теме «Окружность» | 1 |
|
| № 709 710 731 735 |
| 66 | Контрольная работа № 5 по теме « Окружность» | 1 |
| Применяют полученные знания | повтрить |
|
| Повторение | 2 |
|
|
|
| 67 | Четырехугольники. Площади | 1 |
| Повторить и систематизировать понятия четырехугольника и нахождение площадей фигур. | Вопросы к главе |
| 68 | Подобные треугольники. Окружность | 1 |
|
| Вопросы к главе |
ЛИТЕРАТУРА
Геометрия. 8 кл: поурочные планы по учебнику Л.С.Атанасяна, В.Б.Бутузова, С.Б.Кадомцева и др. / авт.-сост. Т.Л.Афонасьева, Л.А.Тапилина. - Волгоград: Учитель, 2006.
Л.С. Атанасян, В.Б.Бутузов, С.Б.Кадомцев и др. «Геометрия 7-9 кл.» - М.: Просвещение, 2018
Оценка качества подготовки выпускников основной школы по математике / Г.В.Дорофеев, Л.В.Кузнецова, Г.М.Кузнецова и др. – М.: Дрофа, 2000
Изучение геометрии в 7-9 классах: Метод. Рекомендации к учеб.: Кн. для учителя / Л.С. Атанасян, В.Б.Бутузов, Ю.А.Глазков и др. – М.: Просвещение, 1999
Программы для общеобразоват. школ, гимназий, лицеев: Математика. 5-11 кл. / Сост. Г.М.Кузнецова, Н.Г. Миндюк. – М.: Дрофа, 2002
Рабинович Е.М. Задачи и упражнения на готовых чертежах. 7-9 классы. Геометрия. – М.: Илекса, Харьков: Гимназия, 1999
Федеральный компонент государственного стандарта общего образования. Математика / Министерство образования РФ. – М., 2004
Геометрия: Разрезные карточки для тестового контроля к учебнику Л.С. Атанасяна. 8 класс /сост. Т.В.Коломиец. – Волгоград: Учитель, 2005
Г.Г. Левитас. Карточки для коррекции знаний по математике для 8-9 классов. – М.: Илекса, 1999
Г.Г. Левитас. Карточки для коррекции знаний по геометрии для 8-9 классов. – М.: Илекса, 2003
| Контрольная работа № 1. Г-8. Вариант-1 № 1. Диагонали прямоугольника ABCD пересекаются в точке О, ∟АВО=360. Найдите угол AOD. № 2. Найдите углы прямоугольной трапеции, если один из его углов равен 200. № 3. Стороны параллелограмма относятся как 1:2, а его периметр равен 30 см. Найдите стороны параллелограмма. № 4. В равнобедренной трапеции сумма углов при большем основании равна 960. Найдите углы трапеции. № 5*. Высота ВМ, проведенная из вершины угла ромба ABCD образует со стороной АВ угол 300, АМ = 4 см. Найдите длину диагонали АD. | Контрольная работа № 1. Г-8. Вариант-2. № 1. Диагонали прямоугольника MNKP пересекаются в точке О, ∟MОN=640. Найдите угол OMP. № 2. Найдите углы равнобедренной трапеции, если один из его углов на 300 больше другого. № 3. Стороны параллелограмма относятся как 3:1, а его периметр равен 40 см. Найдите стороны параллелограмма. № 4. В прямоугольной трапеции разность углов при одной из боковых сторон равна 480. Найдите углы трапеции. № 5*. Высота ВМ, проведенная из вершины угла ромба ABCD образует со стороной АВ угол 300, длина диагонали АС равна 6 см. Найдите AМ, если точка М лежит на продолжении стороны AD. |
| Контрольная работа № 1. Г-8. Вариант-3. № 1. Периметр параллелограмма 50 см. Одна из его сторон на 5 см больше другой. Найдите длины сторон параллелограмма. № 2. Найдите угол между диагоналями прямоугольника, если каждая из них делит угол прямоугольника в отношении 4: 5. № 3. Найдите углы параллелограмма, если одна из его диагоналей является высотой и равна одной из его сторон. № 4. В трапеции ABCD диагональ BD перпендикулярна боковой стороне AB, ∟ADB = ∟BDC = 300. Найдите длину АD, если периметр трапеции равен 60 см. № 5*. В параллелограмме ABCD биссектрисы углов АВС и ВСD пересекаются в точке М. На прямых АВ и СD взяты точки К и Р так, что А –В – К, D – C – P. Биссектрисы углов КВС и ВСР пересекаются в точке М2, М 1М2 = 8см. Найдите AD. | Контрольная работа № 1. Г – 8. Вариант – 4. 1. Периметр параллелограмма 60 см. Одна из его сторон на 6 см меньше другой. Найдите длины сторон параллелограмма. № 2. Угол между диагоналями прямоугольника равен 800. Найдите угол между диагональю и меньшей стороной прямоугольника. № 3. Найдите углы параллелограмма, если одна из его диагоналей является высотой и равна половине неперпендикулярной к ней стороны параллелограмма. № 4. В трапеции ABCD диагональ AС перпендикулярна боковой стороне CD и является биссектрисой угла А. Найдите длину АВ, если периметр трапеции равен 35 см, ∟D = 600. № 5*. В параллелограмме ABCD AD = 6 см. Биссектрисы углов АВС и ВСD пересекаются в точке М. На прямых АВ и СD взяты точки К и Р так, что А –В – К, D – C – P. Биссектрисы углов КВС и ВСР пересекаются в точке М 2. Найдите М1М2.
|
|
|
|
| Контрольная работа № 2. Г-8 Вариант-1. № 1. Сторона треугольника равна 5 см, а высота, проведенная к ней, в два раза больше стороны. Найдите площадь треугольника. № 2. Катеты прямоугольного треугольника равны 6 и 8 см. Найдите гипотенузу и площадь этого треугольника. № 3. Найдите площадь и периметр ромба, если его диагонали равны 8 и 10 см. № 4*. В прямоугольной трапеции АВСК большая боковая сторона равна 3√2 см, угол К равен 450, а высота СН делит основание АК пополам. Найдите площадь трапеции.
| Контрольная работа № 2. Г-8 Вариант-2. № 1. Сторона треугольника равна 12 см, а высота, проведенная к ней, в три раза меньше стороны. Найдите площадь треугольника. № 2. Один из катетов прямоугольного треугольника равен 12 см, а гипотенуза 13 см. Найдите второй катет и площадь этого треугольника. № 3. Диагонали ромба равны 10 и 12 см. Найдите его площадь и периметр. № 4*. В прямоугольной трапеции АВСD большая боковая сторона равна 8 см, угол А равен 600, а высота ВН делит основание АD пополам. Найдите площадь трапеции. |
| Контрольная работа № 2. Г-8 Вариант-3. № 1. Смежные стороны параллелограмма равны 52 см и 30 см, а острый угол равен 300. Найдите площадь параллелограмма. № 2. Вычислите площадь трапеции АВСD с основаниями АD и ВС, если А= 24 см, ВС = 16 см, ∟А= 45, ∟D=90 0. № 3. Дан треугольник АВС. На стороне АС отмечена точка К так, что АК = 6 см, КС = 9 см. Найдите площади треугольников АВК и СВК, если АВ = 13 см, ВС = 14 см. № 4*. Высота равностороннего треугольника равна 6 см. Найдите сумму расстояний от произвольной точки, взятой внутри этого треугольника, до его сторон. | Контрольная работа № 2. Г-8 Вариант-4. № 1.Высота ВК, проведенная к стороне АD параллелограмма АВСD, делит эту сторону на два отрезка АК = 7 см, КD = 15 см. Найдите площадь параллелограмма, если ∟А =450. № 2. Вычислите площадь трапеции АВСD с основаниями АD и ВС, если ВС = 13 см, АD = 27 см, СD = 10см, ∟D = 300. № 3. Дан треугольник МКР. На стороне МК отмечена точка Т так, что МТ= 5 см, КТ = 10 см. Найдите площади треугольников МРТ и КРТ, если МР = 12 см, КР = 9 см. № 4*. В равностороннем треугольнике большая сторона составляет 75% суммы двух других. Точка М, принадлежащая этой стороне, является концом биссектрисы треугольника. Найдите расстояние от точки М до меньшей стороны треугольника, если меньшая высота треугольника равна 4 см.
|
|
|
|
| Контрольная работа № 3. Г-8.  Вариант-1. B Вариант-1. B № 1. Рисунок 1 Дано: ∟А = ∟В, СО = 4, DО = 6, АО = 5. С Найти: а) ОВ; б) АС : ВD; в) SAOC : SBOD. А О D
№ 2. В треугольнике АВС АВ = 4 см, ВС= 7 см, АС = 6 см, а в треугольнике МNК МК = 8 см, МN =12 см, КN = 14 см. Найдите углы треугольника МNК, если ∟А = 80, ∟В = 600. № 3. Прямая пересекает стороны треугольника АВС в точках М и К соответственно так, что МК ║АС, ВМ : АМ = 1: 4. Найдите периметр треугольника ВМК, если периметр треугольника АВС равен 25 см. № 4*. В трапеции АВСD (АD и ВС основания) диагонали пересекаются в точке О, А = 12 см, ВС = 4 см. Найдите площадь треугольника ВОС, если площадь треугольника АОD равна 45 см2.
| Контрольная работа №3. Г-8. Вариант-2. N №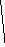 1. Рисунок 1. P 1. Рисунок 1. P Д![]() ано: РЕ ║NК, МР = 8, МN = 12, МЕ = 6. ано: РЕ ║NК, МР = 8, МN = 12, МЕ = 6. Найти: а) МК; б) РЕ : NК; в) SМЕР : SMKN.
M E K № 2. В ∆АВС АВ = 12 см, ВС = 18 см, ∟В = 700,а в ∆ МNК MN = 6 cм, NК = 9 см, ∟N= 700. Найдите сторону АС и угол С треугольника АВС, если МК = 7 см, ∟К = 600. № 3. Отрезки АВ и СD пересекаются в точке О так, что ∟АСО = =∟ВDО, АО : ОВ = 2 : 3. Найдите периметр треугольника АСО, если периметр треугольника ВОD равен 21 см. № 4*. В трапеции АВСD (АD и ВС основания) диагонали пересекаются в точке О, SAOD= 32 см2, S BOC = 8 см2. Найдите меньшее основание трапеции, если большее из них равно 10 см.
|
| Контрольная работа № 3. Г-8. Вариант-3. № 1. Рисунок 1. D B Д   ано: АО = 6,8 см, СО = 8,4 см, ано: АО = 6,8 см, СО = 8,4 см, ОВ = 5,1 см, ОD = 6,3 см. O Доказать: АС ║ВD. Н айти: а) DВ : АС; б) РАОС : РDBO ; айти: а) DВ : АС; б) РАОС : РDBO ; в) SDBO : SAOC A C № 2. Диагонали ромба АВСD пересекаются в точке О, ВD = 16 см. На стороне АВ взята точка К так, что ОК ┴ АВ и ОК = 4√3 см. Найдите сторону ромба и второю диагональ. № 3. В выпуклом четырехугольнике АВСD АВ = 9 см, ВС = 8 см, СD = 16 см, АD = 6 см, ВD = 12 см. Докажите, что АВСD – трапеция. № 4*. В равнобедренном треугольнике МNК с основанием МК, равным 10 см, МN= NК = 20 см. На стороне NК лежит точка А так, что АК : АN= 1 : 3. Найдите АМ. | Контрольная работа № 3. Г-8. Вариант-4. № 1. Рисунок 1. B 1. Рисунок 1. B Дано: ВD = 3,1 см, ВЕ = 4,2 см, ВА = 9,3 см, ВС = 12,6 см. D E Д оказать: DЕ ║АС. оказать: DЕ ║АС. Н![]() айти: а) DЕ : АС; б) РABC : РDBE ; айти: а) DЕ : АС; б) РABC : РDBE ; в) SDBE : SABC. A C № 2. Диагонали ромба АВСD пересекаются в точке О. На стороне АВ взята точка К так, что ОК ┴ АВ, АК = 2 см, ВК = 8 см. Найдите диагонали ромба. № 3. АВСD – выпуклый четырёхугольник, АВ = 6 см, ВС = 9 см, СD = 10 см, DА = 25 см, АС = 15 см. Докажите, что АВСD – трапеция. № 4*. В равнобедренном треугольнике АВС АВ = ВС = 40 см, АС = 20 см. На стороне ВС отмечена точка Н так, что ВН : НС = 3 : 1. Найдите АН.
|
|
Контрольная работа № 4. Г-8. Вариант-1. № 1. Средние линии треугольника относятся как 2: 2: 4, а периметр треугольника равен 45 см. Найдите стороны треугольника. № 2. Медианы треугольника АВС пересекаются в точке О. Через точку О проведена прямая, параллельная стороне АС пересекающая стороны АВ и ВС в точках Е и F соответственно. Найдите ЕF, если сторона АС равна 15 см. № 3. В прямоугольном треугольнике АВС (∟С= 900) АС = 5 см, ВС = 5√3 см. Найдите угол В и гипотенузу АВ. № 4. В треугольнике АВС ∟А =α, ∟С =β, сторона ВС = 7 см, ВН-высота. Найдите АН. № 5. В трапеции АВСD продолжения боковых сторон пересекаются в точке К, причем точка В-середина отрезка АК. Найдите сумму оснований трапеции, если АD = 12 см. |
Контрольная работа №4. Г-8. Вариант-2. № 1. Средние линии треугольника относятся как 4: 5: 6, а периметр треугольника, образованного средними линиями, равен 30 см. Найдите средние линии треугольника. № 2. Медианы треугольника MNK пересекаются в точке О. Через точку О проведена прямая, параллельная стороне MK пересекающая стороны MN и NK в точках A и B соответственно. Найдите MK, если длина отрезка АB равна 12 см. №3. В прямоугольном треугольнике РКТ (∟Т= 900), РТ = 7√3 см, КТ= 7 см. Найдите угол К и гипотенузу КР. № 4. В треугольнике АВС ∟А =α, ∟С =β , высота ВН равна 4 см. Найдите АС. № 5. В трапеции MNKP продолжения боковых сторон пересекаются в точке E, причем EK=KP. Найдите разность оснований трапеции, если NK = 7 см. |
| Контрольная работа № 4. Г-8. Вариант-3. № 1. На стороне ВС треугольника АВС выбрана точка D так, что ВD: DС = 3:2, точка К – середина отрезка АВ, точка F–середина отрезка АD, КF =6 см, ∟АDС=1000. Найдите ВС и ∟АFК. № 2. В прямоугольном треугольнике АВС ∟С= 900, АС = 4 см, СВ = 4√3 см, СМ –медиана. Найдите угол ВСМ. № 3. В равнобедренной трапеции основания равны 8 см и 12 см, меньший угол равен α . Найдите периметр и площадь трапеции. № 4.В равнобедренном треугольнике АВС с основанием АС медианы пересекаются в точке О. Найдите площадь треугольника АВС, если ОА =13 см, ОВ = 10 см. № 5. В трапеции АВС (ВС ║АD) АВ ┴ ВD, ВD =2√5 , AD =2√10, СЕ – высота треугольника ВСD, а tg∟ECD= 3. Найдите ВЕ. | Контрольная работа № 4. Г-8. Вариант-4. № 1. На стороне АМ треугольника АВМ отмечена точка Н так, что АН: НЬ = 4:7; точка С – середина стороны АВ, точка О –середина стороны отрезка ВН, АМ = 22 см, ∟ВОС = 1050. Найдите СО и угол ВНМ. № 2. В прямоугольном треугольнике MNK ∟K= 90, KM = 6см, NК =6√3 см, КD- медиана. Найдите угол КDN. № 3. В равнобедренной трапеции боковая сторона равна 6 см, меньшее основание 10 см, а меньший угол α . Найдите площадь трапеции. № 4. В прямоугольном треугольнике АВС (∟С =900) медианы пересекаются в точке О, ОВ = 10 см, ВС = 12 см. Найдите гипотенузу треугольника. № 5. В трапеции АВСD ∟А =90, АС= 6√2, ВС=6, DЕ –высота треугольника АСD, tg∟ACD= 2. Найдите СЕ. |
| Контрольная работа № 5. Г-8. Вариант-1. № 1. АВ и АС- отрезки касательных, проведенных к окружности радиуса 9 см. Найдите длины отрезков АС и АО, если АВ = 12 см. № 2. Рисунок 1. Дано: ᵕАВ : ᵕВС = 11 : 12. Н айдите ∟ВСА, ∟ВАС. айдите ∟ВСА, ∟ВАС. ![]()  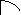 B A B A ![]()

130O C № 3. Хорды MN и PK пересекаются точке E так, что ME =12 см, NE =3 см, PE=KE. Найдите PK. № 4.Окружность с центром в точке О радиусом 16 см описана около треугольника ABC так, что ∟OAB=300, ∟OCB=450. Найдите стороны AB и BC треугольника. | Контрольная работа № 5. Г-8. Вариант-2. № 1. MN и MK-отрезки касательных, проведенных к окружности радиуса 5 см. Найдите MN и MK, если МО= 13 см. № 2. Рисунок 1. Дано: ᵕАВ : ᵕАС = 5 : 3. Н айдите ∟ВОС, ∟АВС. айдите ∟ВОС, ∟АВС. 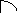 A B A B ![]() 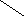  ![]()  60O 60O
C O № 3. Хорды АВ и СD пересекаются точке F так, что АF =4 см, ВF =16 см, СF=DF. Найдите CD. № 4.Окружность с центром в точке О радиусом 12 см описана около треугольника MNK так, что ∟MON=1200, ∟NOK=900. Найдите стороны MN и NK треугольника. |
| Контрольная работа № 5. Г-8. Вариант-3. № 1. В треугольник вписана окружность так, что три из шести получившихся отрезков касательных равны 3 см,4 см,5 см. Определите вид треугольника № 2. Точки А и В делят окружность с центром О на дуги АВМ и АСВ так, что дуга АСВ на 600 меньше дуги АМВ. АМ- диаметр окружности. Найдите углы АМВ, АВМ, АСВ. № 3. Хорды АВ и СD пересекаются в точке Е так, что АЕ=3 см, ВЕ=36 см, СЕ: DЕ =3:4. Найдите СD и наименьшее значение радиуса этой окружности. № 4. В равнобедренном треугольнике боковая сторона равна 10 см, а биссектриса, проведенная к основанию 8 см. Найдите радиус окружности, вписанной в этот треугольник, и радиус окружности, описанной около этого треугольника.
| Контрольная работа № 5. Г-8. Вариант-4. № 1. В прямоугольный треугольник вписана окружность радиусом 2 см так, что один из получившихся отрезков касательных равен 4 см. Найдите стороны треугольника, если его периметр равен 24 см. № 2.Точки Е и Н делят окружность с центром О на дуги ЕАН и ЕКН так, что дуга ЕКН на 900 меньше дуги ЕАН, ЕА- диаметр окружности. Найдите углы ЕКА, ЕАН, ЕКН. № 3. Хорды МN и РК пересекаются в точке А так, что МА= 3 см, NА= 16 см, РА: КА= 1: 3. Найдите РК и наименьшее значение радиуса этой окружности. № 4. В равнобедренном треугольнике основание равно 10 см, а высота, Проведенная к ней, 12 см. Найдите радиус окружности, вписанной в этот треугольник, и радиус окружности, описанной около этого треугольника. |







 Вариант-1. B
Вариант-1. B 1. Рисунок 1. P
1. Рисунок 1. P

 ано: АО = 6,8 см, СО = 8,4 см,
ано: АО = 6,8 см, СО = 8,4 см,  1. Рисунок 1. B
1. Рисунок 1. B оказать: DЕ ║АС.
оказать: DЕ ║АС. айдите ∟ВСА, ∟ВАС.
айдите ∟ВСА, ∟ВАС.
 B A
B A
 A B
A B

 60O
60O









