РАБОЧАЯ ПРОГРАММА
ПО УЧЕБНОМУ ПРЕДМЕТУ
«математика»
5-9 класс, Основное общее образование(ФГОС)
Асташенко Светлана Анатольевна, учитель математики,
учитель высшей квалификационной категории
Составлена на основании: Примерные программы по учебным предметам.
Математика 5 – 9 классы.руководитель А.А. Кузнецов Серия: стандарты второго поколения,
Личностные, предметные и метапредметные результаты изучения математики
В направлении личностного развития:
умение ясно, точно, грамотно излагать свои мысли в устной и письменной
речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации;
креативность мышления, инициатива, находчивость, активность при решении математических задач;
умение контролировать процесс и результат учебной математической деятельности;
способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
формирование представлений о математике, как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;
развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;
формирование интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
формирование качеств мышления, необходимых для адаптации в современном информационном обществе;
развитие интереса к математическому творчеству и математических способностей;
В предметном направлении:
овладение базовым понятийным аппаратом по основным разделам содержания, представление об основных изучаемых понятиях (число, геометрическая фигура, уравнение, функция, вероятность) как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления;
умение работать с математическим текстом (анализировать, извлекать необходимую информацию), грамотно применять математическую терминологию и символику, использовать различные языки математики;
умение проводить классификации, логические обоснования, доказательства математических утверждений;
умение распознавать виды математических утверждений (аксиомы, определения, теоремы и др.), прямые и обратные теоремы;
развитие представлений о числе и числовых системах от натуральных до действительных чисел, овладение навыками устных, письменных, инструментальных вычислений;
овладение символьным языком алгебры, приемами выполнения тождественных преобразований рациональных выражений, решения уравнений, систем уравнений, неравенств и систем неравенств, умение использовать идею координат на плоскости для интерпретации уравнений, неравенств, систем, умение применять алгебраические преобразования, аппарат уравнений и неравенств для решения задач из различных разделов курса;
овладение системой функциональных понятий, функциональным языком и символикой, умение на основе функционально-графических представлений описывать и анализировать реальные зависимости;
овладение основными способами представления и анализа статистических данных; наличие представлений о статистических закономерностях в реальном мире и о различных способах их изучения, о вероятностных моделях;
овладение геометрическим языком, умение использовать его для описания предметов окружающего мира, развитие пространственных представлений и изобразительных умений, приобретение навыков геометрических построений;
усвоение систематических знаний о плоских фигурах и их свойствах, а также на наглядном уровне — о простейших пространственных телах, умение применять систематические знания о них для решения геометрических и практических задач;
умения измерять длины отрезков, величины углов, использовать формулы для нахождения периметров, площадей и объемов геометрических фигур;
умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочных материалов, калькулятора, компьютера.
• овладение математическими знаниями и умениями, необходимыми для продолжения образования, изучения смежных дисциплин, применения в повседневной жизни;
• создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.
Задачи:
овладеть системой математических знаний и умений, необходимых для применения в практической деятельности, изучении смежных дисциплин;
способствовать интеллектуальному развитию, формировать качества, необходимые человеку для полноценной жизни в современном обществе, свойственные математической деятельности: ясности и точности мысли, интуиции, логического мышления, пространственных представлений, способности к преодолению трудностей;
формировать представления об идеях и методах математики как универсального языка науки и техники, средствах моделирования явлений и процессов;
воспитывать культуру личности, отношение кматематики как части общечеловеческой культуры, играющей особую роль в общественном развитии.
В метапредметном направлении:
развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;
первоначальные представления об идеях и о методах математики как универсальном языке науки и техники, средстве моделирования явлений и процессов;
умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
умение находить в различных источниках информацию, необходимую для решения математических проблем, представлять ее в понятной форме, принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
умение понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;
умение выдвигать гипотезы при решении учебных задач, понимать необходимость их проверки;
умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
Содержание учебного предмета
Содержание математического образования в основной школе формируется на основе фундаментального ядра школьного математического образования. Оно в основной школе включает следующие разделы: арифметика, алгебра, функции, вероятность и статистика, геометрия. Наряду с этим в него включены два дополнительных раздела: логика и множества, математика в историческом развитии, что связано с реализацией целей общеинтеллектуального и общекультурного развития учащихся. Содержание каждого из этих разделов разворачивается в содержательно-методическую линию, пронизывающую все основные разделы содержания математического образования на данной ступени обучения.
Содержание раздела «Арифметика» служит базой для дальнейшего изучения учащимися математики, способствует развитию их логического мышления, формированию умения пользоваться алгоритмами, а также приобретению практических навыков, необходимых в повседневной жизни. Развитие понятия о числе в основной школе связано с рациональными и иррациональными числами, формированием первичных представлений о действительном числе. Завершение числовой линии (систематизация сведений о действительных числах, о комплексных числах), так же как и более сложные вопросы арифметики (алгоритм Евклида, основная теорема арифметики), отнесено к ступени общего среднего (полного) образования.
Содержание раздела «Алгебра» направлено на формирование у учащихся математического аппарата для решения задач из разных разделов математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей процессов и явлений реального мира. В задачи изучения алгебры входят также развитие алгоритмического мышления, необходимого, в частности, для усвоения курса информатики, овладения навыками дедуктивных рассуждений. Преобразование символьных форм вносит специфический вклад в развитие воображения учащихся, их способностей к математическому творчеству. В основной школе материал группируется вокруг рациональных выражений, а вопросы, связанные с иррациональными выражениями, с тригонометрическими функциями и преобразованиями, входят в содержание курса математики на старшей ступени обучения в школе.
Содержание раздела «Функции» нацелено на получение школьниками конкретных знаний о функции как важнейшей математической модели для описания и исследования разнообразных процессов. Изучение этого материала способствует развитию у учащихся умения использовать различные языки математики (словесный, символический, графический), вносит вклад в формирование представлений о роли математики в развитии цивилизации и культуры.
Раздел «Вероятность и статистика» — обязательный компонент школьного образования, усиливающий его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования у учащихся функциональной грамотности - умений воспринимать и критически анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, проводить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит учащимся рассматривать случаи, осуществлять перебор и подсчет числа вариантов, в том числе в простейших прикладных задачах.
При изучении статистики и вероятности расширяются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации, и закладываются основы вероятностного мышления.
Цель содержания раздела «Геометрия» — развить у учащихся пространственное воображение и логическое мышление путем систематического изучения свойств геометрических фигур на плоскости и в пространстве и применения этих свойств при решении задач вычислительного и конструктивного характера. Существенная роль при этом отводится развитию геометрической интуиции. Сочетание наглядности со строгостью является неотъемлемой частью геометрических знаний. Материал, относящийся к блокам «Координаты» и «Векторы», в значительной степени несет в себе межпредметные знания, которые находят применение, как в различных математических дисциплинах, так и в смежных предметах.
Особенностью раздела «Логика и множества» является то, что представленный в нем материал преимущественно изучается и используется в ходе рассмотрения различных вопросов курса. Соответствующий материал нацелен на математическое развитие учащихся, формирование у них умения точно, сжато и ясно излагать мысли в устной и письменной речи.
Раздел «Математика в историческом развитии» предназначен для формирования представлений о математике как части человеческой культуры, для общего развития школьников, для создания культурно-исторической среды обучения. На него не выделяется специальных уроков, усвоение его не контролируется, но содержание этого раздела органично присутствует в учебном процессе как своего рода гуманитарный фон при рассмотрении проблематики основного содержания математического образования.
Арифметика (240час)
Натуральные числа.
Натуральный ряд. Десятичная система счисления. Арифметические действия с натуральными числами. Свойства арифметических действий.
Степень с натуральным показателем.
Числовые выражения, значение числового выражения. Порядок действий в числовых выражениях, использование скобок. Решение текстовых задач арифметическими способами.
Делители и кратные. Свойства и признаки делимости. Простые и составные числа. Разложение натурального числа на простые множители. Деление с остатком.
Дроби.
Обыкновенные дроби. Основное свойство дроби. Сравнение обыкновенных дробей. Арифметические действия с обыкновенными дробями. Нахождение части от целого и целого по его части.
Десятичные дроби. Сравнение десятичных дробей. Арифметические действия с десятичными дробями. Представление десятичной дроби в виде обыкновенной дроби и обыкновенной в виде десятичной.
Проценты; нахождение процентов от величины и величины по ее процентам. Отношение; выражение отношения в процентах. Пропорция; основное свойство пропорции.
Решение текстовых задач арифметическими способами.
Рациональные числа.
Положительные и отрицательные числа, модуль числа. Множество целых чисел. Множество рациональных чисел; рациональное число как отношение m/n, где т — целое число, п— натуральное число. Сравнение рациональных чисел. Арифметические действия с рациональными числами. Свойства арифметических действий. Степень с целым показателем.
Действительные числа.
Квадратный корень из числа. Корень третьей степени.
Понятие об иррациональном числе. Иррациональность числа ��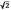
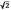 и несоизмеримость стороны и диагонали квадрата. Десятичные приближения иррациональных чисел.
и несоизмеримость стороны и диагонали квадрата. Десятичные приближения иррациональных чисел.
Множество действительных чисел; представление действительных чисел в виде бесконечных десятичных дробей. Сравнение действительных чисел.
Координатная прямая. Изображение чисел точками координатной прямой. Числовые промежутки.
Измерения, приближения, оценки.
Размеры объектов окружающего мира (от элементарных частиц до Вселенной), длительность процессов в окружающем мире. Выделение множителя степени 10 в записи числа.
Приближенное значение величины, точность приближения. Округление натуральных чисел и десятичных дробей. Прикидка и оценка результатов вычислений.
Алгебра(200час)
Алгебраические выражения.
Буквенные выражения (выражения с переменными). Числовое значение буквенного выражения. Допустимые значения переменных. Подстановка
выражений вместо переменных. Преобразование буквенных выражений на основе свойств арифметических действий. Равенство буквенных выражений. Тождество.
Степень с натуральным показателем и ее свойства. Одночлены и многочлены. Степень многочлена. Сложение, вычитание, умножение многочленов. Формулы сокращенного умножения: квадрат суммы и квадрат разности. Формула разности квадратов. Преобразование целого выражения в многочлен. Разложение многочленов на множители. Многочлены с одной переменной. Корень многочлена. Квадратный трехчлен; разложение квадратного трехчлена на множители.
Алгебраическая дробь. Основное свойство алгебраической дроби. Сложение, вычитание, умножение, деление алгебраических дробей. Степень с целым показателем и ее свойства.
Рациональные выражения и их преобразования. Доказательство тождеств.
Квадратные корни. Свойства арифметических квадратных корней и их применение к преобразованию числовых выражений и вычислениям.
Уравнения.
Уравнение с одной переменной. Корень уравнения. Свойства числовых равенств. Равносильность уравнений.
Линейное уравнение. Квадратное уравнение: формула корней квадратного уравнения. Теорема Виета. Решение уравнений, сводящихся к линейным и квадратным. Примеры решения уравнений третьей и четвертой степени. Решение дробно-рациональных уравнений.
Уравнение с двумя переменными. Линейное уравнение с двумя переменными, примеры решения уравнений в целых числах.
Система уравнений с двумя переменными. Равносильность систем. Системы двух линейных уравнений с двумя переменными; решение подстановкой и сложением. Примеры решения систем нелинейных уравнений с двумя переменными.
Решение текстовых задач алгебраическим способом.
Декартовы координаты на плоскости. Графическая интерпретация уравнения с двумя переменными. График линейного уравнения с двумя переменными; угловой коэффициент прямой; условие параллельности прямых. Графики простейших нелинейных уравнений: парабола, гипербола, окружность. Графическая интерпретация систем уравнений с двумя переменными.
Неравенства.
Числовые неравенства и их свойства. Неравенство с одной переменной. Равносильность неравенств. Линейные неравенства с одной переменной. Квадратные неравенства. Системы неравенств с одной переменной.
Функции(65час)
Основные понятия.
Зависимости между величинами. Понятие функции. Область определения и множество значений функции. Способы задания функции. График функции. Свойства функций, их отображение на графике. Примеры графиков зависимостей, отражающих реальные процессы.
Числовые функции.
Функции, описывающие прямую и обратную пропорциональные зависимости, их графики и свойства. Линейная функция, ее график и свойства. Квадратичная функция, ее график и свойства. Степенные функции с натуральными показателями 2 и 3, их графики и свойства. Графики функции у = IxI
Числовые последовательности.
Понятие числовой последовательности. Задание последовательности рекуррентной формулой и формулой л-го члена.
Арифметическая и геометрическая прогрессии. Формулы л-го члена арифметической и геометрической прогрессий, суммы первых пчленов. Изображение членов арифметической и геометрической прогрессий точками координатной плоскости. Линейный и экспоненциальный рост. Сложные проценты.
Вероятность и статистика(50час)
Описательная статистика.
Представление данных в виде таблиц, диаграмм, графиков. Случайная изменчивость. Статистические характеристики набора данных: среднее арифметическое, медиана, наибольшее и наименьшее значения, размах. Представление о выборочном исследовании.
Случайные события и вероятность.
Понятие о случайном опыте и случайном событии. Частота случайного события. Статистический подход к понятию вероятности. Вероятности противоположных событий. Достоверные и невозможные события. Равновозможность событий. Классическое определение вероятности.
Комбинаторика.
Решение комбинаторных задач перебором вариантов. Комбинаторное правило умножения. Перестановки и факториал.
Геометрия(255час)
Основные свойства простейших геометрических фигур
Начальные понятия планиметрии. Геометрические фигуры. Точка и прямая. Отрезок, длина отрезка и её свойства. Полуплоскость. Полупрямая. Угол, величина угла и её свойства. Треугольник. Равенство отрезков, углов, треугольников. Параллельные прямые. Теоремы и доказательства. Аксиомы.
Смежные и вертикальные углы Смежные и вертикальные углы и их свойства. Перпендикулярные прямые. Биссектриса угла и её свойства.
Признаки равенства треугольников Признаки равенства треугольников. Медианы, биссектрисы и высоты треугольника. Равнобедренный треугольник и его свойства.
Сумма углов треугольника Параллельные прямые. Основное свойство параллельных прямых. Признаки параллельности прямых. Сумма углов треугольника. Внешний угол треугольника. Признаки равенства прямоугольных треугольников. Расстояние от точки до прямой. Расстояние между параллельными прямыми.
Геометрические построения
Окружность. Касательная к окружности и её свойства. Окружность, описанная около треугольника. Окружность, вписанная в треугольник. Свойство серединного перпендикуляра к отрезку. Основные задачи на построение с помощью циркуля и линейки.
Четырехугольники
Определение четырехугольника. Параллелограмм и его свойства. Признаки параллелограмма. Прямоугольник, ромб, квадрат и их свойства. Теорема Фалеса. Средняя линия треугольника. Трапеция. Средняя линия трапеция. Пропорциональные отрезки. Основная цель – дать учащимся систематизированные сведения о четырехугольниках и их свойствах.
Теорема Пифагора
Синус, косинус и тангенс острого угла прямоугольного треугольника. Теорема Пифагора. Неравенство треугольника. Перпендикуляр и наклонная. Соотношение между сторонами и углами в прямоугольном треугольнике. Значения синуса, косинуса и тангенса некоторых углов.
Декартовы координаты на плоскости
Прямоугольная система координат на плоскости. Координаты середины отрезка. Расстояние между точками. Уравнения прямой и окружности. Координаты пересечения прямых. График линейной функции. Пересечение прямых с окружностью. Синус, косинус, тангенс углов от 0° до 180°.
Движение
Движение и его свойства. Симметрия относительно точки и прямой. Поворот. Параллельный перенос и его свойства. Понятие о равенстве фигур.
Векторы
Вектор. Абсолютная величина и направление вектора. Равенство векторов. Координаты вектора. Сложение векторов и его свойства. Умножение вектора на число [Коллинеарные векторы] Скалярное произведение векторов. Угол между векторами. [Проекция на ось.Разложение вектора по координатным осям.]
Движения.
Отображение плоскости на себя. Понятие движения. Осевая и центральная симметрии. Параллельный перенос. Поворот. Наложения и движения.
Об аксиомах геометрии.
Беседа об аксиомах геометрии.
Начальные сведения из стереометрии.
Предмет стереометрии. Геометрические тела и поверхности. Многогранники: призма, параллелепипед, пирамида» формулы для вычисления их объемов. Тела и поверхности вращения: цилиндр, конус, сфера, шар, формулы для вычисления их площадей поверхностей и объемов.
Логика и множества (10час)
Теоретико-множественные понятия.
Множество, элемент множества. Задание множеств перечислением элементов, характеристическим свойством. Стандартные обозначения числовых множеств. Пустое множество и его обозначение. Подмножество. Объединение и пересечение множеств.
Иллюстрация отношений между множествами с помощью диаграмм Эйлера — Венна.
Элементы логики.
Определение. Аксиомы и теоремы. Доказательство. Доказательство от противного. Теорема, обратная данной. Пример и контрпример.
Понятие о равносильности, следовании, употребление логических связок, если то в том и только в том случае, логические связки и, или.
Математика в историческом развитии
История формирования понятия числа: натуральные числа, дроби, недостаточность рациональных чисел для геометрических измерений, иррациональные числа. Старинные системы записи чисел. Дроби в Вавилоне, Египте, Риме. Открытие десятичных дробей. Старинные системы мер. Десятичные дроби и метрическая система мер. Появление отрицательных чисел и нуля. Л. Магницкий. Л. Эйлер.
Зарождение алгебры в недрах арифметики. Ал-Хорезми. Рождение буквенной символики. П. Ферма, Ф. Виет, Р. Декарт. История вопроса о нахождении формул корней алгебраических уравнений, неразрешимость в радикалах уравнений степени, большей четырех. Н. Тарталья, Дж. Кардано, Н. X. Абель, Э. Галуа.
Изобретение метода координат, позволяющего переводить геометрические объекты на язык алгебры. Р. Декарт и П. Ферма. Примеры различных систем координат на плоскости.
Задача Леонардо Пизанского (Фибоначчи) о кроликах, числа Фибоначчи. Задача о шахматной доске.
Истоки теории вероятностей: страховое дело, азартные игры. П. Ферма и Б. Паскаль. Я. Бернулли. А. Н. Колмогоров.
От землемерия к геометрии. Пифагор и его школа. Фалес. Архимед. Построение правильных многоугольников. Трисекция угла. Квадратура круга. Удвоение куба. История числа л. Золотое сечение. «Начала» Евклида. Л. Эйлер. Н. И. Лобачевский. История пятого постулата.
Софизмы, парадоксы.Резерв времени 20час
| Год обучения | Количество часов в неделю | Количество учебных недель | Всего часов за учебный год |
| 5 класс | 5 | 34 | 170 |
| 6 класс | 5 | 34 | 170 |
| 7класс | 5 | 34 | 170 |
| 8класс | 5 | 34 | 170 |
| 9 класс | 5 | 34 | 170 |
Тематическое планирование
МАТЕМАТИКА
5—6 классы (340ч)
| Натуральные числа.50часов Натуральный ряд. Десятичная система счисления. Арифметические действия с натуральными числами. Свойства арифметических действий. Понятие о степени с натуральным показателем. Квадрат и куб числа. Числовые выражения, значение числового выражения. Порядок действий в числовых выражениях, использование скобок. Решение текстовых задач арифметическими способами. Делители и кратные. Наибольший общий делитель; наименьшее общее кратное. Свойства делимости. Признаки делимости на 2, 3, 5, 9, 10. Простые и составные числа. Разложение натурального числа на простые множители. Деление с остатком |
| Дроби.120часов Обыкновенные дроби. Основное свойство дроби. Сравнение обыкновенных дробей. Арифметические действия с обыкновенными дробями. Нахождение части от целого и целого по его части. Десятичные дроби. Сравнение десятичных дробей. Арифметические действия с десятичными дробями. Представление десятичной дроби в виде обыкновенной дроби и обыкновенной в виде десятичной. Отношение. Пропорция; основное свойство пропорции. Проценты; нахождение процентов от величины и величины по ее процентам; выражение отношения в процентах. Решение текстовых задач арифметическими способами |
| Рациональные числа. 40часов Положительные и отрицательные числа, модуль числа. Изображение чисел точками координатной прямой; геометрическая интерпретация модуля числа. Множество целых чисел. Множество рациональных чисел. Сравнение рациональных чисел. Арифметические действия с рациональными числами. Свойства арифметических действий |
| Измерения, приближения, оценки 20часов Примеры зависимостей между величинами скорость, время, расстояние; производительность, время, работа; цена, количество, стоимость и др. Представление зависимостей в виде формул. Вычисления по формулам. Решение текстовых задач арифметическими способами |
| Элементы алгебры 25часов. Использование букв для обозначения чисел, для записи свойств арифметических действий. Буквенные выражения (выражения с переменными). Числовое значение буквенного выражения. Уравнение, корень уравнения. Нахождение неизвестных компонентов арифметических действий. Декартовы координаты на плоскости. Построение точки по ее координатам, определение координат точки на плоскости |
| Вероятность 15часов Представление данных в виде таблиц, диаграмм. Понятие о случайном опыте и событии. Достоверное и невозможное события. Сравнение шансов. Решение комбинаторных задач перебором вариантов |
| Наглядная геометрия 40часов Наглядные представления о фигурах на плоскости: прямая, отрезок, луч, угол, ломаная, многоугольник, правильный многоугольник, окружность, круг. Четырехугольник, прямоугольник, квадрат. Треугольник, виды треугольников. Изображение геометрических фигур. Взаимное расположение двух прямых, двух окружностей, прямой и окружности. Длина отрезка, ломаной. Периметр многоугольника. Единицы измерения длины. Измерение длины отрезка, построение отрезка заданной длины. Угол. Виды углов. Градусная мера угла. Измерение и построение углов с помощью транспортира. Понятие площади фигуры; единицы измерения площади. Площадь прямоугольника и площадь квадрата. Равновеликие фигуры. Наглядные представления о пространственных фигурах: куб, параллелепипед, призма, пирамида, шар, сфера, конус, цилиндр. Изображение пространственных фигур. Примеры сечений. Многогранники, правильные многогранники. Примеры разверток многогранников, цилиндра и конуса. Понятие объема; единицы объема. Объем прямоугольного параллелепипеда и объем куба. Понятие о равенстве фигур. Центральная, осевая и зеркальная симметрии. Изображение симметричных фигур
|
Математика 7-9 классы ( 510ч)
| Действителные числа 15 часов Расширение множества натуральных чисел до множества целых, множества целых чисел до множества рациональных. Рациональное число как отношение т/п, где т — целое число, а п — натуральное число. Степень с целым показателем. Квадратный корень из числа. Корень третьей степени. Понятие об иррациональном числе. Иррациональность числа��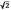 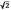 и несоизмеримость стороны и диагонали квадрата. Десятичные приближения иррациональных чисел. и несоизмеримость стороны и диагонали квадрата. Десятичные приближения иррациональных чисел. Множество действительных чисел; представление действительных чисел в виде бесконечных десятичных дробей. Сравнение действительных чисел. Взаимно однозначное соответствие между действительными числами и точками координатной прямой. Числовые промежутки: интервал, отрезок, луч |
| Измерения, приближения, оценки 10часов Приближенное значение величины, точность приближения. Размеры объектов окружающего мира (от элементарных частиц до Вселенной), длительность процессов в окружающем мире. Выделение множителя — степени 10 в записи числа. Прикидка и оценка результатов вычислений |
| Введение в алгебру 8часов Буквенные выражения (выражения с переменными). Числовое значение буквенного выражения. Допустимые значения переменных. Подстановка выражений вместо переменных. Преобразование буквенных выражений на основе свойств арифметических действий. Равенство буквенных выражений. Тождество |
| Многочлены 45 часов Степень с натуральным показателем и ее свойства. Одночлены и многочлены. Степень многочлена. Сложение, вычитание, умножение многочленов. Формулы сокращенного умножения: квадрат суммы и квадрат разности. Формула разности квадратов. Преобразование целого выражения в многочлен. Разложение многочлена на множители: вынесение общего множителя за скобки, группировка, применение формул сокращенного умножения. Многочлены с одной переменной. Корень многочлена. Квадратный трехчлен, разложение квадратного трехчлена на множители
|
| Алгебраические дроби. 22 часа Алгебраическая дробь. Основное свойство алгебраической дроби. Сокращение дробей. Сложение, вычитание, умножение, деление алгебраических дробей. Степень с целым показателем и ее свойства. Рациональные выражения и их преобразования. Доказательство тождеств |
| Квадратные корни 12 часов Понятия квадратного корня, арифметического квадратного корня. Уравнение вида х2=а. Свойства арифметических квадратных корней: корень из произведения, частного, степени; тождества. Применение свойств арифметических квадратных корней для преобразования числовых выражений и вычислений |
| Уравнение с одной переменной 38 часов Уравнение с одной переменной. Корень уравнения. Свойства числовых равенств. Равносильность уравнений. Линейное уравнение. Решение уравнений, сводящихся к линейным. Квадратное уравнение. Неполные квадратные уравнения. Формула корней квадратного уравнения. Теорема Виета. Решение уравнений, сводящихся к квадратным. Биквадратное уравнение. Примеры решения уравнений третьей и четвертой степени разложением на множители. Решение дробно-рациональных уравнений. Решение текстовых задач алгебраическим способом |
| Системы уравнений 30 часов Уравнение с двумя переменными. Линейное уравнение с двумя переменными. Примеры решения уравнений в целых числах. Система уравнений с двумя переменными. Равносильность систем уравнений. Система двух линейных уравнений с двумя переменными; решение подстановкой и сложением. Решение систем двух уравнений, одно из которых линейное, а другое второй степени. Примеры решения систем нелинейных уравнений. Решение текстовых задач алгебраическим способом. Декартовы координаты на плоскости. Графическая интерпретация уравнения с двумя переменными. График линейного уравнения с двумя переменными, угловой коэффициент прямой; условие параллельности прямых. Графики простейших нелинейных уравнений (парабола, гипербола, окружность). Графическая интерпретация системы уравнений с двумя переменными |
| Неравенства 20 часов Числовые неравенства и их свойства. Неравенство с одной переменной. Равносильность неравенств. Линейные неравенства с одной переменной. Квадратные неравенства. Системы линейных неравенств с одной переменной |
| Зависимость между величинами.15 часов Зависимость между величинами. Представление зависимостей между величинами в виде формул. Вычисления по формулам. Прямая пропорциональная зависимость: задание формулой, коэффициент пропорциональности; свойства. Примеры прямо пропорциональных зависимостей. Обратная пропорциональная зависимость: задание формулой, коэффициент обратной пропорциональности; свойства. Примеры обратных пропорциональных зависимостей. Решение задач на прямую пропорциональность и обратную пропорциональную зависимости |
| Числовые функции 35 часов Понятие функции. Область определения и множество значений функции. Способы задания функции. График функции. Свойства функции, их отображение на графике: возрастание и убывание функции, нули функции, сохранение знака. Чтение и построение графиков функций. Примеры графиков зависимостей, отражающих реальные процессы. Функции, описывающие прямую и обратную пропорциональные зависимости, их графики. Линейная функция, ее график и свойства. Квадратичная функция, ее график и свойства. Степенные функции с натуральными показателями 2и3, их графики и свойства. Графики функций �� |
| Арифметическая, геометрическая прогрессии 15 часов Понятие числовой последовательности. Задание последовательности рекуррентной формулой и формулой n-го члена. Арифметическая и геометрическая прогрессии. Формулы n-го члена арифметической и геометрической прогрессий, суммы первых п членов. Изображение членов арифметической и геометрической прогрессий точками координатной плоскости. Линейный и экспоненциальный рост. Сложные проценты |
| Описательная статистика 10 часов Представление данных в виде таблиц, диаграмм, графиков. Случайная изменчивость. Статистические характеристики набора данных: среднее арифметическое, медиана, наибольшее и наименьшее значения, размах. Представление о выборочном исследовании |
| Элементы комбинаторики 10 часов ешение комбинаторных задач перебором вариантов. Комбинаторное правило умножения. Перестановки и факториал
|
| Элементы логики 5 часов Множество, элемент множества. Задание множеств перечислением элементов, характеристическим свойством. Стандартные обозначения числовых множеств. Пустое множество и его обозначение. Подмножество. Объединение и пересечение множеств, разность множеств. Иллюстрация отношений между множествами с помощью диаграмм Эйлера — Венна. Понятия о равносильности, следовании, употребление логических связок если то, в том и только том случае. Логические связкии, или |
| Прямые углы 15 часов Геометрические фигуры. Точка, прямая, плоскость. Отрезок, луч. Угол. Прямой угол, острый и тупой углы, развернутый угол. Вертикальные и смежные углы. Биссектриса угла и ее свойство. Свойства углов с параллельными и перпендикулярными сторонами. Взаимное расположение прямых на плоскости: параллельные и пересекающиеся прямые. Перпендикулярные прямые. Теоремы о параллельности и перпендикулярности прямых. Перпендикуляр и наклонная к прямой. Серединный перпендикуляр к отрезку. Свойства биссектрисы угла и серединного перпендикуляра к отрезку.
|
| Треугольники 65 часов Треугольники. Прямоугольные, остроугольные и тупоугольные треугольники. Высота, медиана, биссектриса, средняя линия треугольника. Равнобедренные и равносторонние треугольники; свойства и признаки равнобедренного треугольника. Признаки равенства треугольников. Признаки равенства прямоугольных треугольников. Неравенство треугольника. Соотношения между сторонами и углами треугольника. Сумма углов треугольника. Внешние углы треугольника, теорема о внешнем угле треугольника. Теорема Фалеса. Подобие треугольников; коэффициент подобия. Признаки подобия треугольников. Теорема Пифагора. Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника и углов от 0 до 180°; приведение к острому углу. Решение прямоугольных треугольников. Основное тригонометрическое тождество. Формулы, связывающие синус, косинус, тангенс, котангенс одного и того же угла. Решение треугольников: теорема косинусов и теорема синусов. Замечательные точки треугольника: точки пересечения серединных перпендикуляров, биссектрис, медиан, высот и их продолжений |
| Четырехугольники 20 часов Четырехугольник. Параллелограмм, теоремы о свойствах сторон, углов и диагоналей параллелограмма и его признаки. Прямоугольник, теорема о равенстве диагоналей прямоугольника. Ромб, теорема о свойстве диагоналей. Квадрат. Трапеция, средняя линия трапеции; равнобедренная трапеция |
| Многоугольник 10 часов Многоугольник. Выпуклые многоугольники. Правильные многоугольники. Теорема о сумме углов выпуклого многоугольника. Теорема о сумме внешних углов выпуклого многоугольника |
| Окружность и круг 20 часов Окружность и круг. Центр, радиус, диаметр. Дуга, хорда. Сектор, сегмент. Центральный, вписанный угол, величина вписанного угла. Взаимное расположение прямой и окружности, двух окружностей. Касательная и секущая к окружности, их свойства. Вписанные и описанные многоугольники. Окружность, вписанная в треугольник, и окружность, описанная около треугольника. Теоремы о существовании окружности, вписанной в треугольник, и окружности, описанной около треугольника. Вписанные и описанные окружности правильного многоугольника. Формулы для вычисления стороны правильного многоугольника; радиуса окружности, вписанной в правильный многоугольник; радиуса окружности, описанной около правильного многоугольника |
| Геометрические преобразования 10 часов Понятие о равенстве фигур. Понятие движения: осевая и центральная симметрии, параллельный перенос, поворот. Понятие о подобии фигур и гомотетии |
| Построения с помощью циркуля и линейки 5 часов Построения с помощью циркуля и линейки. Основные задачи на построение: деление отрезка пополам; построение угла, равного данному; построение треугольника по трем сторонам; построение перпендикуляра к прямой; построение биссектрисы угла; деление отрезка на правных частей |
| Измерение геометрических величин 25 часов Длина отрезка. Длина ломаной. Периметр многоугольника. Расстояние от точки до прямой. Расстояние между параллельными прямыми. Длина окружности, число л; длина дуги окружности. Градусная мера угла, соответствие между величиной центрального угла и длиной дуги окружности. Понятие площади плоских фигур. Равносоставленные и равновеликие фигуры. Площадь прямоугольника. Площади параллелограмма, треугольника и трапеции (основные формулы). Формулы, выражающие площадь треугольника через две стороны и угол между ними, через периметр и радиус вписанной окружности; формула Герона. Площадь многоугольника. Площадь круга и площадь сектора. Соотношение между площадями подобных фигур |
| Координаты 10 часов Декартовы координаты на плоскости. Уравнение прямой. Координаты середины отрезка. Формула расстояния между двумя точками плоскости. Уравнение окружности |
| Векторы 10 часов Вектор. Длина (модуль) вектора. Равенство векторов. Коллинеарные векторы. Координаты вектора. Умножение вектора на число, сумма векторов, разложение вектора по двум неколлинеарным векторам. Угол между векторами. Скалярное произведение вектор |
| Элементы логики 5 часов Определение. Аксиомы и теоремы. Доказательство. Доказательство от противного. Теорема, обратная данной. Пример и контрпример |
Оценочные материалы для достижения обучающимися предметных результатов
| тема | Формы контроля | источник |
| 5класс |
| М.К. Потапов, А.В. Шевкин.Математика. Дидактические материалы. 5 класс. Москва, Просвещение, 2017г |
| Глава 1. Натуральные числа и нуль. | Самостоятельные работы: 1 - 6 Контрольная работа №1 - 2 |
| Глава 2. Измерение величин. | Самостоятельные работы:7 - 11 Контрольная работа №3 - 4. |
| Глава 3. Делимость натуральных чисел. | Самостоятельные работы:12 Контрольная работа №5. |
| Глава 4. Обыкновенные дроби. | Самостоятельные работы:13-23 Контрольная работа №6 - 8. |
| 6класс |
| М.К. Потапов, А.В. Шевкин.Математика. Дидактические материалы. 6 класс. Москва, Просвещение, 2017г |
| Глава 1. Отношения, пропорции, проценты | Самостоятельные работы:1-7 Контрольная работа №1. |
| Глава 2. Целые числа. | Самостоятельные работы:8-12 Контрольная работа №2-3 |
| Глава 3. Рациональные числа. | Самостоятельные работы:13-25 Контрольная работа №4-5 |
| Глава 4. Десятичные дроби. | Самостоятельные работы:26-34 Контрольная работа №6-7 |
|
| Глава 5. Обыкновенные и десятичные дроби. | Самостоятельные работы:35-39 Контрольная работа №8-9 |
|
| 7класс. алгебра Глава1.Выражения, Глава тождества, уравнения.
|
Самостоятельные работы 1-6, контрольная работа №1,2
| Л.И. Звавич, Л.В. Кузнецова,С.Б. Суворова «Дидактические материалы .Алгебра 7 класс» Издательство «Просвещение», М, 2012
|
| Глава2.Функции. | Самостоятельные работы 7-17, контрольная работа №3
|
| Глава3. Степень с натуральным показателем | Самостоятельные работы 18-24, контрольная работа №4
|
| Глава 4 Многочлены | Самостоятельные работы 37-44, контрольная работа №5-7
|
| Глава5 Формулы сокращенного умножения
| Самостоятельные работы 25-35, контрольная работа №8
|
| Глава 6 Системы линейных уравнений | Самостоятельные работы 45-50, контрольная работа №9
|
| 7класс. Геометрия Глава1. Начальные геометрические сведения | Самостоятельные работы 1-6, контрольная работа №1
| М.А. Иченская «Геометрия. Контрольные и самостоятельные работы » Издательство «Просвещение», М, 2017 |
| Глава2. Треугольники | Самостоятельные работы 7-10, контрольная работа №2,3
|
| Глава3. Параллельные прямые | Самостоятельные работы 11-12, контрольная работа №4
|
| Глава 4. Соотношение между сторонами и углами треугольника | Самостоятельные работы 13-16, контрольная работа №5
|
| 8класс алгебра Глава1. Рациональные дроби | Самостоятельные работы 1-12, контрольная работа №1,2
| В.И. Жохов,Ю.Н.Макарычев, Н.Г. Миндюк, «Дидактические материалы .Алгебра 8 класс» Издательство «Просвещение», М, 2012 |
| Глава2 Квадратные корни | Самостоятельные работы 13-22, контрольная работа №3,4
|
| Глава3.Квадратные уравнения | Самостоятельные работы 23-31, контрольная работа №5,6
|
| Глава4. Неравенства | Самостоятельные работы 32-45, контрольная работа №7,8
|
| Глава5. Степень с целым показателем. Элементы статистики | Самостоятельные работы 47-57, контрольная работа №9 контрольная работа №10-итоговая
|
| 8класс геометрия Глава 5.Четырехугольники | Самостоятельные работы1-4, контрольная работа №1
| М.А. Иченская «Геометрия. Контрольные и самостоятельные работы » Издательство «Просвещение», М, 2017 |
| Глава6. Площадь | Самостоятельные работы 5-7, контрольная работа №2
|
| Глава7. Подобные треугольники | Самостоятельные работы 8-10, контрольная работа №3
|
| Глава4 Окружность. | Самостоятельные работы 11-15, контрольная работа №4-5
|
| 9класс алгебра глава 1Квадратичная функция.
| Самостоятельные работы1-11, контрольная работа №1,2
| Ю.Н.Макарычев, Н.Г. Миндюк, Л.Б. Крайнева «Дидактические материалы .Алгебра 9 класс» Издательство «Просвещение», М, 2012 |
| Глава 2 Уравнения и неравенства с одной переменной. | Самостоятельные работы 12-18, контрольная работа №3,4
|
| Глава3 Уравнения и неравенства с двумя переменными. | Самостоятельные работы 19-24, контрольная работа №5,6
|
| Глава4. Арифметическая и геометрическая прогрессии. | Самостоятельные работы 25-29, контрольная работа №7,8
|
| Глава5. Элементы комбинаторики и теории вероятностей. | Самостоятельные работы 30-32, контрольная работа №9 контрольная работа №10-итоговая
|
| 9класс геометрия Глава1. Векторы | Самостоятельные работы 1-, контрольная работа №1
| М.А. Иченская «Геометрия. Контрольные и самостоятельные работы » Издательство «Просвещение», М, 2017 |
| Глава2. Метод координат | Самостоятельные работы 2-3, контрольная работа №1
|
| Глава3. Соотношения между сторонами и углами треугольника | Самостоятельные работы 4-6, контрольная работа №2
|
| Глава4 Длина окружности, площадь круга | Самостоятельные работы 7-10, контрольная работа №3
|
| Глава 5. Движение | Самостоятельные работы 11-13, контрольная работа №4
|
| Глава 6. Начальные сведения из стереометрии | Ознакомительно Итоговая контрольная работа №5
|
19