А дминистрация г. Улан-Удэ
дминистрация г. Улан-Удэ
Комитет по образованию
МАОУ «Средняя общеобразовательная школа № 57 г.Улан-Удэ имени А. Цыденжапова»
РАБОЧАЯ ПРОГРАММА
| Предмет (курс, дисциплина) | Алгебра |
| Класс | 8б 8в |
| Уровень образования | Основное общее |
| Количество часов в неделю | 3 |
| ФИО учителя | Прушенова Светлана Александровна |
| Должность учителя | Учитель математики |
| Квалификационная категория | Первая |
| Срок действия программы | 1 год |
Пояснительная записка
Рабочая программа по алгебре для 8 класса составлена в соответствии с правовыми и нормативными документами:
Федеральный Закон «Об образовании в Российской Федерации» (от 29.12. 2012 г. № 273-ФЗ) (с изменениями);
Федеральный государственный образовательный стандарт основного общего образования, утвержденным приказом Министерства образования и науки Российской Федерации от 17.12.2010 №1897 (далее – ФГОС основного общего образования) (в ред. Приказов Минобрнауки России от 29.12.2014 N 1644, от 31.12.2015 N 1577);
Приказ Министерства просвещения Российской Федерации от 08.05.2019 г. № 233 «О внесении изменений в федеральный перечень учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования, утвержденный приказом Министерства просвещения Российской Федерации от 28.12.2018 г. № 345.
Рабочая программа по предмету «Алгебра», 8 класс составлена на основе Федерального Государственного Образовательного Стандарта основного общего образования, примерной программы: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир, Е.В. Буцко Математика: программы: 5 – 9 классы – 2 изд., доработано. – М.: Вентана - Граф, 2013. – 112 с.
УМК: «Алгебра 8 класс» авторов А.Г. Мерзляка, В.Б. Полонского, М.С. Якира.
Программа рассчитана на 3 часа в неделю, всего 102 часа (34 недели) и соответствует федеральному государственному образовательному стандарту основного общего образования.
Цели и задачи изучения учебного предмета
- овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
- интеллектуальное развитие, формирования качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
- формирование представлений об идеях и методах математики как средства моделирования явлений и процессов;
- воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
Планируемые результаты изучения предмета
Программа обеспечивает достижения следующих результатов освоения образовательной программы основного общего образования:
Личностные результаты:
воспитание российской гражданской идентичности: патриотизма, уважения к Отечеству, осознания вклада отечественных учёных в развитие мировой науки;
ответственное отношение к учению, готовность и способность обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию;
осознанный выбор и построение дальнейшей индивидуальной траектории образования на базе ориентировки в мире профессий и профессиональных предпочтений с учётом устойчивых познавательных интересов, а также на основе формирования уважительного отношения к труду, развитие опыта участия в социально значимом труде;
умение контролировать процесс и результат учебной и математической деятельности;
критичность мышления, инициатива, находчивость, активность при решении математических задач.
Метапредметные результаты:
умение самостоятельно определять цели своего обучения, ставить и формулировать для себя новые задачи в учёбе, развивать мотивы и интересы своей познавательной деятельности;
умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией;
умение определять понятия, создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации;
умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и делать выводы;
развитие компетентности в области использования информационно-коммуникационных технологий;
первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
умение находить в различных источниках информацию, необходимую для решения математических задач, и представлять её в понятной форме, принимать решение в условиях неполной или избыточной, точной или вероятностной информации;
умение понимать и использовать математические средства наглядности (графики, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;
умение выдвигать гипотезы при решении задачи, понимать необходимость их проверки;
понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.
Предметные результаты:
осознание значения математики для повседневной жизни человека;
представление о математической науке как сфере математической деятельности, об этапах её развития, о её значимости для развития цивилизации;
развитие умений работать с учебным математическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли с применением математической терминологии и символики, проводить классификации, логические обоснования;
владение базовым понятийным аппаратом по основным разделам содержания;
систематические знания о функциях и их свойствах;
практически значимые математические умения и навыки, их применение к решению математических и нематематических задач предполагающее умения:
выполнять вычисления с действительными числами;
решать уравнения, неравенства, системы уравнений и неравенств;
решать текстовые задачи арифметическим способом, с помощью составления и решения уравнений, систем уравнений и неравенств;
использовать алгебраический язык для описания предметов окружающего мира и создания соответствующих математических моделей;
проверить практические расчёты: вычисления с процентами, вычисления с числовыми последовательностями, вычисления статистических характеристик, выполнение приближённых вычислений;
выполнять тождественные преобразования рациональных выражений;
выполнять операции над множествами;
исследовать функции и строить их графики;
читать и использовать информацию, представленную в виде таблицы, диаграммы (столбчатой или круговой);
решать простейшие комбинаторные задачи.
Тематическое планирование
| № п/п | Раздел | Кол-во часов | Контроль |
| 1 | Рациональные выражения. | 44 | Контрольная работа №1 Контрольная работа №2 Контрольная работа №3 Самостоятельная работа - 14 |
| 2 | Квадратные корни. Действительные числа | 25 | Контрольная работа №4 Самостоятельная работа - 9 |
| 3 | Квадратные уравнения | 26 | Контрольная работа №5 Контрольная работа №6 Самостоятельная работа - 9 |
| 4 | Повторение и систематизация учебного материала | 7 | Итоговая контрольная работа № 7 |
|
| Всего: | 102 |
|
Содержание учебного предмета
| № п/п | Раздел | Кол-во часов | Содержание | Планируемые результаты обучения |
| 1 | Рациональные выражения. | 44 | Рациональные дроби. Основное свойство рациональной дроби. Сложение и вычитание рациональных дробей с одинаковыми знаменателями. Сложение и вычитание рациональных дробей с разными знаменателями. Умножение и деление рациональных дробей. Возведение рациональной дроби в степень. Тождественные преобразования рациональных выражений. Равносильные уравнения. Рациональные уравнения. Степени с целым отрицательным показателем. Свойства степени с целым показателем. Функция 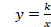 и её график. и её график. | Ученик научится: • осуществлять в рациональных выражениях числовые подстановки и выполнять соответствующие вычисления; • выполнять преобразования дробно-рациональных выражений: сокращение дробей, приведение алгебраических дробей к общему знаменателю, сложение, умножение, деление алгебраических дробей, возведение алгебраической дроби в натуральную и целую отрицательную степень; • выполнять разложение многочлена на множители применением формул сокращенного умножения; • выполнять несложные преобразования дробно-линейных выражений; оперировать понятием степень с целым отрицательным показателем; • выполнять преобразования выражений, содержащих степени с целыми отрицательными показателями, переходить от записи в виде степени с целым отрицательным показателем к записи в виде дроби; • решать простейшие рациональные уравнения; • понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных реальных ситуаций, решать текстовые задачи алгебраическим методом; • устанавливать, при каких значениях переменной алгебраическая дробь не имеет смысла и равна 0. Ученик получит возможность научиться: • выполнять многошаговые преобразования рациональных выражений, применяя широкий набор способов и приёмов; • выбирать рациональный способ решения; • давать определения алгебраическим понятиям; • работать с заданными алгоритмами; • работать с текстами научного стиля, составлять конспект; • осуществлять сравнение, самостоятельно выбирая основания и критерии для указанных логических операций; • формулировать собственное мнение и позицию, аргументировать и координировать её с позициями партнёров в сотрудничестве при выработке общего решения в совместной деятельности; • работать в группе — устанавливать рабочие отношения, эффективно сотрудничать и способствовать продуктивной кооперации. |
| 2 | Квадратные корни. Действительные числа | 25 | Функция 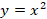 и её график. Квадратные корни. и её график. Квадратные корни. Арифметический квадратный корень. Множество и его элементы. Подмножество. Операции над множествами. Числовые множества. Свойства арифметического квадратного корня. Тождественные преобразования выражений, содержащих арифметические квадратные корни. Функция 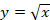 и её график. и её график. | Ученик научится: • оперировать на базовом уровне понятиями: натуральное число, целое число, обыкновенная дробь, десятичная дробь, смешанная дробь, рациональное число, иррациональное число, действительные числа; • округлять числа, записывать их в стандартном виде; • использовать начальные представления о множестве действительных чисел; • распознавать рациональные и иррациональные числа; • использовать в ходе решения задач элементарные представления, связанные с приближёнными значениями величин; • упрощать выражения, используя определение степени с отрицательным показателем и свойства степени, выполнять преобразования выражений, содержащих степень с отрицательным показателем; • оперировать понятиями «тождество», «тождественное преобразование»; доказывать тождества; • находить область определения и область значений функции, читать график функции; • строить графики функций 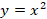 , функции , функции 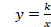 , проверять, является ли данный график графиком заданной функции (линейной, квадратичной, обратной пропорциональности); , проверять, является ли данный график графиком заданной функции (линейной, квадратичной, обратной пропорциональности); • выполнять простейшие преобразования графиков функций; • строить график квадратичной функции, по графику находить область определения, множество значений, нули функции, промежутки знакопостоянства, промежутки возрастания и убывания, наибольшее и наименьшее значения функции; • графически решать уравнения и системы уравнений; • графически определять число решений системы уравнений; • понимать функцию как важнейшую математическую модель для описания процессов и явлений окружающего мира, применять функциональный язык для описания и исследования зависимостей между физическими величинами; • упрощать функциональные выражения; • строить графики кусочно-заданных функций; • работать с чертёжными инструментами. В повседневной жизни и при изучении других предметов: • использовать графики реальных процессов и зависимостей для определения их свойств (наибольшие и наименьшие значения, промежутки возрастания и убывания, области положительных и отрицательных значений и т.п.); • строить график функции 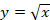 , описывать её свойства; , описывать её свойства; • освобождаться от иррациональности в знаменателе; • раскладывать выражения на множители, способом группировки, используя определение и свойства квадратного корня, формулы квадратов суммы и разности; • оценивать не извлекаемые корни, находить их приближенные значения; • выполняют преобразования иррациональных выражений: сокращать дроби, раскладывая выражения на множители. Ученик получит возможность научиться: • развить представление о числе и числовых системах от натуральных до действительных чисел; о роли вычислений в практике; • развить и углубить знания о десятичной записи действительных чисел (периодические и непериодические дроби); • понять, что числовые данные, которые используются для характеристики объектов окружающего мира, являются преимущественно приближёнными, что по записи приближённых значений, содержащихся в информационных источниках, можно судить о погрешности приближения; • понять, что погрешность результата вычислений должна быть соизмерима с погрешностью исходных данных; • самостоятельно задумывать, планировать и выполнять учебное исследование. • выполнять многошаговые преобразования рациональных выражений, применяя широкий набор способов и приёмов; • выбирать рациональный способ решения; • давать определения алгебраическим понятиям; • работать с заданными алгоритмами; • работать с текстами научного стиля, составлять конспект; • осуществлять сравнение, самостоятельно выбирая основания и критерии для указанных логических операций; • формулировать собственное мнение и позицию, аргументировать и координировать её с позициями партнёров в сотрудничестве при выработке общего решения в совместной деятельности; • работать в группе — устанавливать рабочие отношения, эффективно сотрудничать и способствовать продуктивной кооперации; • проводить исследования, связанные с изучением свойств функций, в том числе с использованием компьютера; на основе графиков изученных функций строить более сложные графики (кусочно-заданные, с «выколотыми» точками и т. п.); • использовать функциональные представления и свойства функций для решения математических задач из различных разделов курса; • строить графики с использованием возможностей специальных компьютерных инструментов и программ; • задавать вопросы, необходимые для организации собственной деятельности и сотрудничества с партнёром; • осуществлять взаимный контроль и оказывать в сотрудничестве необходимую взаимопомощь; • на основе комбинирования ранее изученных алгоритмов и способов действия решать нетиповые задачи, выполняя продуктивные действия эвристического типа. В повседневной жизни и при изучении других предметов: • иллюстрировать с помощью графика реальную зависимость или процесс по их характеристикам; • использовать свойства и график квадратичной функции при решении задач из других учебных предметов. • свободно работать с текстами научного стиля; • делать умозаключения (индуктивное и по аналогии) и выводы на основе аргументации, формулировать выводы; • участвовать в диалоге, аргументировано отстаивать свою точку зрения; • понимать точку зрения собеседника, признавать право на иное мнение; • осуществлять проверку выводов, положений, закономерностей, теорем; • осуществлять контроль, коррекцию, оценку действий партнёра, уметь убеждать; • развить представление о числе и числовых системах от натуральных до действительных чисел; о роли вычислений в практике; • составлять план и последовательность действий в связи прогнозируемым результатом; • осуществлять контроль, коррекцию, оценку действий партнер.
|
| 3 | Квадратные уравнения | 26 | Квадратные уравнения. Решение неполных квадратных уравнений. Формула корней квадратного уравнения. Теорема Виета. Квадратный трёхчлен. Решение уравнений, сводящихся к квадратным уравнениям. Рациональные уравнения как математические модели реальных ситуаций. | Ученик научится: • оперировать на базовом уровне понятиями: равенство, числовое равенство, уравнение, корень уравнения, решение уравнения; • решать квадратные уравнения по формуле корней квадратного уравнения; • решать разными способами основные виды квадратных уравнений с одной переменной; • понимать уравнение как важнейшую модель для описания и изучения разнообразных реальных ситуаций; • решать задачи разных типов, связывающих три величины, выделять эти величины и отношения между ними; • строить модель условия задачи (в виде таблицы, схемы, рисунка), с целью поиска решения задачи; • осуществлять способ поиска решения задачи, в котором рассуждение строится от условия к требованию или от требования к условию; • составлять план решения задачи; • выделять этапы решения задачи; • интерпретировать вычислительные результаты в задаче, исследовать полученное решение задачи; • знать различие скоростей объекта в стоячей воде, против течения и по течению реки. В повседневной жизни и при изучении других предметов: • составлять и решать квадратные уравнения при решении задач, возникающих в других учебных предметах; • выдвигать гипотезы о возможных предельных значениях искомых в задаче величин (делать прикидку). • решать квадратные уравнения, корнями которых являются иррациональные числа; • решать простейшие иррациональные уравнения; оперировать понятиями: неполные квадратные уравнения, квадратные уравнения • решать неполные квадратные уравнения; • решать квадратные уравнения по формуле корней квадратного уравнения; • решать задачи с помощью квадратных уравнений; решать задачи разных типов (на работу, на покупки, на движение), связывающих три величины, выделять эти величины и отношения между ними; осознавать и объяснять идентичность задач разных типов, связывающих три величины (на работу, на покупки, на движение), выделять эти величины и отношения между ними, применять их при решении задач, конструировать собственные задач указанных типов; • формулировать и применять теорему Виета и обратную ей теорему; • раскладывать на множители квадратный трёхчлен; • решать дробно - рациональные и рациональные уравнения; • решать задачи с помощью рациональных уравнений, выделяя три этапа математического моделирования; • решать рациональные уравнения, используя метод введения новой переменной; • решать биквадратные уравнения; • решать простейшие иррациональные уравнения. Ученик получит возможность научиться: • выбирать рациональный способ решения; • давать определения алгебраическим понятиям; • работать с заданными алгоритмами; • работать с текстами научного стиля, составлять конспект; • осуществлять сравнение, самостоятельно выбирая основания и критерии для указанных логических операций; • формулировать собственное мнение и позицию, аргументировать и координировать её с позициями партнёров в сотрудничестве при выработке общего решения в совместной деятельности; • работать в группе — устанавливать рабочие отношения, эффективно сотрудничать и способствовать продуктивной кооперации; • задавать вопросы, необходимые для организации собственной деятельности и сотрудничества с партнёром; • осуществлять взаимный контроль и оказывать в сотрудничестве необходимую взаимопомощь; • на основе комбинирования ранее изученных алгоритмов и способов действия решать нетиповые задачи, выполняя продуктивные действия эвристического типа. В повседневной жизни и при изучении других предметов: • делать умозаключения (индуктивное и по аналогии) и выводы на основе аргументации, формулировать выводы; • участвовать в диалоге, аргументировано отстаивать свою точку зрения; • понимать точку зрения собеседника, признавать право на иное мнение; • осуществлять проверку выводов, положений, закономерностей, теорем; • осуществлять контроль, коррекцию, оценку действий партнёра, уметь убеждать; • решать квадратные уравнения выделением квадрата двучлена; • решать квадратные уравнения с параметрами и проводить исследование всех корней квадратного уравнения; • выполнять равносильные переходы при решении иррациональных уравнений разной степени трудности; • овладеть специальными приёмами решения уравнений и систем уравнений; уверенно применять аппарат уравнений для решения разнообразных задач из математики, смежных предметов, практики; • применять графические представления для исследования уравнений, систем уравнений, содержащих параметр; • составлять план и последовательность действий в связи прогнозируемым результатом; • осуществлять контроль, коррекцию, оценку действий партнер.
|
| 4 | Повторение и систематизация учебного материала | 7 | Повторение и систематизация учебного материала за курс алгебры 8 класса. | Обобщить приобретенные знания, навыки и умения за 8 класс. Ученик получит возможность применять приобретенные знания, умения, навыки, в конкретной деятельности. Проводить исследования связанные с изучением свойств функций, в том числе с использованием компьютера; осознавать значение математики для повседневной жизни человека. |
|
| ИТОГО | 102 |
|
|
Материально-техническое обеспечение образовательного процесса
Литература:
1. Учебники:
Алгебра : 8 класс : учебник для учащихся общеобразовательных организаций / А. Г. Мерзляк, В. Б. Полонский, М. С. Якир. – 2-е изд., дораб. – М. : Вентана-Граф, 2018. – 272 с. : ил.
2. Методическая литература:
Алгебра : 8 класс : методическое пособие / Е. В. Буцко, А. Г. Мерзляк, В. Б. Полонский, М. С. Якир. – М. : Вентана-Граф, 2018. – 189 с. : ил.
Система оценки планируемых результатов
Одним из направлений оценочной деятельности в соответствии с требованиями Стандарта является оценка образовательных достижений учащихся.
Система оценки достижения планируемых результатов по алгебре направлена на обеспечение качества математического образования. Она должна позволять отслеживать индивидуальную динамику развития учащихся, обеспечивать обратную связь для учителей и, учащихся и родителей.
Формирование личностных результатов обеспечивается в ходе реализации всех компонентов образовательного процесса, включая внеурочную деятельность, реализуемую семьёй и школой.
Основным объектом оценки личностных результатов служит сформированность универсальных учебных действий, включаемых в следующие три основных блока:
Сформированность основ гражданской идентичности личности;
Готовность к переходу к самообразованию на основе учебно-познавательной мотивации, в том числе готовность к выбору направления профильного образования;
Сформированность социальных компетенций, включая ценностно-смысловые установки и моральные нормы, опыт социальных и межличностных отношений, правосознание.
Основным объектом оценки метапредметных результатов является:
Способность и готовность к освоению систематических знаний по алгебре, их самостоятельному пополнению, переносу и интеграции;
Способность к сотрудничеству и коммуникации в ходе учебной и внеучебной деятельности;
Способность и готовность к использованию ИКТ в целях обучения и развития;
Способность к самоорганизации, саморегуляции и рефлексии.
Основным объектом оценки предметных результатов по алгебре в соответствии с требованиями Стандарта является способность к решению учебно-познавательных и учебно-практических задач, основанных на изучаемом учебном материале, с использованием способов действий, релевантных содержанию учебных предметов, в том числе метапредметных (познавательных, регулятивных, коммуникативных) действий.
Основными видами оценивания образовательных достижений по математике являются стартовое. Текущее и итоговое.
Стартовое оценивание позволяет спланировать личностно-ориентированное обучение, индивидуализировать образовательный процесс.
Текущее оценивание позволяет определить уровень усвоения нового материала. Степень самостоятельности учащихся при решении задач, характер применения рациональных способов решения задач и др. Для текущего оценивания используются следующие методы контроля.
Устный контроль: фронтальный опрос, индивидуальный опрос;
Письменный контроль: математический диктант, самостоятельная работа, контрольная работа, реферат, тест;
Практический контроль: фронтальная или индивидуальная практическая работа, домашняя контрольная работа, исследовательская работа, проектная работа.
Итоговое оценивание может проводиться после завершения темы, раздела, учебного курса основной или старшей школы (в частности, в виде итоговой аттестации). Итоговая оценка результатов освоения учащимися основной образовательной программы выставляется по результатам промежуточной и итоговой аттестации и формируется на основе:
Результатов внутришкольного мониторинга образовательных достижений по алгебре, зафиксированных в оценочных листах, в том числе за промежуточные и итоговые работы на мепредметной основе;
Оценок за выполнение итоговых работ по алгебре;
Оценки за выполнение и защиту индивидуального проекта;
Оценок за работы, выносимые на государственную итоговую аттестацию (ГИА) и единый государственный экзамен (ЕГЭ).
Особенности оценки предметных результатов
Оценка предметных результатов представляет собой оценку достижения обучающимся планируемых результатов по отдельным предметам.
Формирование этих результатов обеспечивается за счёт основных компонентов образовательного процесса — учебных предметов.
Основным объектом оценки предметных результатов в соответствии с требованиями Стандарта является способность к решению учебно-познавательных и учебно-практических задач, основанных на изучаемом учебном материале, с использованием способов действий, релевантных содержанию учебных предметов, в том числе метапредметных (познавательных, регулятивных, коммуникативных) действий.
Система оценки предметных результатов освоения учебных программ с учётом уровневого подхода, принятого в Стандарте, предполагает выделение базового уровня достижений как точки отсчёта при построении всей системы оценки и организации индивидуальной работы с обучающимися.
Реальные достижения обучающихся могут соответствовать базовому уровню, а могут отличаться от него как в сторону превышения, так и в сторону недостижения.
Практика показывает, что для описания достижений обучающихся целесообразно установить следующие пять уровней.
Базовый уровень достижений — уровень, который демонстрирует освоение учебных действий с опорной системой знаний в рамках диапазона (круга) выделенных задач. Овладение базовым уровнем является достаточным для продолжения обучения на следующей ступени образования, но не по профильному направлению. Достижению базового уровня соответствует отметка «удовлетворительно» (или отметка «3», отметка «зачтено»).
Превышение базового уровня свидетельствует об усвоении опорной системы знаний на уровне осознанного произвольного овладения учебными действиями, а также о кругозоре, широте (или избирательности) интересов. Целесообразно выделить следующие два уровня, превышающие базовый:
повышенный уровень достижения планируемых результатов, оценка «хорошо» (отметка «4»);
высокий уровень достижения планируемых результатов, оценка «отлично» (отметка «5»).
Повышенный и высокий уровни достижения отличаются по полноте освоения планируемых результатов, уровню овладения учебными действиями и сформированностью интересов к данной предметной области.
Индивидуальные траектории обучения обучающихся, демонстрирующих повышенный и высокий уровни достижений, целесообразно формировать с учётом интересов этих обучающихся и их планов на будущее. При наличии устойчивых интересов к учебному предмету и основательной подготовки по нему такие обучающиеся могут быть вовлечены в проектную деятельность по предмету и сориентированы на продолжение обучения в старших классах по данному профилю.
Для описания подготовки учащихся, уровень достижений которых ниже базового, целесообразно выделить также два уровня:
пониженный уровень достижений, оценка «неудовлетворительно» (отметка «2»);
низкий уровень достижений, оценка «плохо» (отметка «1»).
Недостижение базового уровня (пониженный и низкий уровни достижений) фиксируется в зависимости от объёма и уровня освоенного и неосвоенного содержания предмета.
Как правило, пониженный уровень достижений свидетельствует об отсутствии систематической базовой подготовки, о том, что обучающимся не освоено даже и половины планируемых результатов, которые осваивает большинство обучающихся, о том, что имеются значительные пробелы в знаниях, дальнейшее обучение затруднено. При этом обучающийся может выполнять отдельные задания повышенного уровня. Данная группа обучающихся (в среднем в ходе обучения составляющая около 10%) требует специальной диагностики затруднений в обучении, пробелов в системе знаний и оказании целенаправленной помощи в достижении базового уровня.
Низкий уровень освоения планируемых результатов свидетельствует о наличии только отдельных фрагментарных знаний по предмету, дальнейшее обучение практически невозможно. Обучающимся, которые демонстрируют низкий уровень достижений, требуется специальная помощь не только по учебному предмету, но и по формированию мотивации к обучению, развитию интереса к изучаемой предметной области, пониманию значимости предмета для жизни и др. Только наличие положительной мотивации может стать основой ликвидации пробелов в обучении для данной группы обучающихся.
Критерии и нормы оценки знаний, умений и навыков обучающихся по математике.
1. Оценка письменных контрольных работ обучающихся по математике.
Отметка «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Отметка «1» ставится, если:
работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2. Оценка устных ответов обучающихся по математике
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Отметка «1» ставится, если:
ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу.
Общая классификация ошибок
При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
Грубыми считаются ошибки:
незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
незнание наименований единиц измерения;
неумение выделить в ответе главное;
неумение применять знания, алгоритмы для решения задач;
неумение делать выводы и обобщения;
неумение читать и строить графики;
неумение пользоваться первоисточниками, учебником и справочниками;
потеря корня или сохранение постороннего корня;
отбрасывание без объяснений одного из них;
равнозначные им ошибки;
вычислительные ошибки, если они не являются опиской;
логические ошибки.
К негрубым ошибкам следует отнести:
неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного — двух из этих признаков второстепенными;
неточность графика;
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
нерациональные методы работы со справочной и другой литературой;
неумение решать задачи, выполнять задания в общем виде.
Недочетами являются:
нерациональные приемы вычислений и преобразований;
небрежное выполнение записей, чертежей, схем, графиков.
Контроль ЗУН предлагается при проведении математических диктантов, практических работ, самостоятельных работ обучающего и контролирующего вида, контрольных работ.
Контрольно-измерительные материалы «Алгебра -8» КОНТРОЛЬНАЯ РАБОТА ПО АЛГЕБРЕ № 1 ПО ТЕМЕ: «ОСНОВНОЕ СВОЙСТВО РАЦИОНАЛЬНОЙ ДРОБИ.СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ» 8 КЛАСС ВАРИАНТ 1
|
Отметка | «3» | «4» | «5» |
| 7 заданий | 9 заданий | 12-14 заданий |

КОНТРОЛЬНАЯ РАБОТА ПО АЛГЕБРЕ № 1 ПО ТЕМЕ: «ОСНОВНОЕ СВОЙСТВО РАЦИОНАЛЬНОЙ ДРОБИ.СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ». 8 КЛАСС. ВАРИАНТ 2
|
Отметка | «3» | «4» | «5» |
| 7 заданий | 9 заданий | 12-14 заданий |

Контрольная работа по алгебре № 2
по теме: «Умножение и деление рациональных дробей. Тождественные преобразования рациональных выражений »8 класс.
|
Отметка | «3» | «4» | «5» |
| 7 заданий | 9 заданий | 11-12 заданий |
В а р и а нт I

Контрольная работа по алгебре № 2
по теме: «Умножение и деление рациональных дробей. Тождественные преобразования рациональных выражений »8 класс
|
Отметка | «3» | «4» | «5» |
| 7 заданий | 9 заданий | 11-12 заданий |
Вариант 2

Контрольная работа № 3 по алгебре в 8 классе
по теме «Равносильные уравнения. Рациональные уравнения. Степень с целым отрицательным показателем. Функция у=к/х и ее график»
|
Отметка | «3» | «4» | «5» |
| 6 заданий | 9 заданий | 12-15 заданий |
Вариант I

Контрольная работа № 3 по алгебре в 8 классе
по теме «Равносильные уравнения. Рациональные уравнения. Степень с целым отрицательным показателем. Функция у=к/х и ее график»
|
Отметка | «3» | «4» | «5» |
| 6 заданий | 9 заданий | 12-15 заданий |
Вариант 2

Контрольная работа по алгебре № 4 ПО ТЕМЕ: «КВАДРАТНЫЕ КОРНИ. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА» в 8 классе
|
Отметка | «3» | «4» | «5» |
| 7 заданий | 9 заданий | 12-14 заданий |
Вариант I

Контрольная работа по алгебре № 4 ПО ТЕМЕ: «КВАДРАТНЫЕ КОРНИ. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА» в 8 классе
|
Отметка | «3» | «4» | «5» |
| 7 заданий | 9 заданий | 12-14 заданий |
Вариант 2.

Контрольная работа по алгебре №5
по теме: "Квадратные уравнения. Теорема Виета". 8кл.
|
Отметка | «3» | «4» | «5» |
| 7 заданий | 8-9 заданий | 10-11 заданий |
Вариант I

Контрольная работа по алгебре №5
по теме: "Квадратные уравнения. Теорема Виета". 8кл.
|
Отметка | «3» | «4» | «5» |
| 7 заданий | 8-9 заданий | 10-11 заданий |
 Вариант 2
Вариант 2
Контрольная работа по алгебре № 6
по теме: "Квадратный трехчлен. Решение уравнений, сводящихся к квадратным.
Рациональные уравнения как математические модели реальных ситуаций.
Деление многочленов".8кл.
|
Отметка | «3» | «4» | «5» |
| 3 задания | 4-5заданий | 6-7 заданий |
Вариант I

Контрольная работа по алгебре № 6
по теме: "Квадратный трехчлен. Решение уравнений, сводящихся к квадратным.
Рациональные уравнения как математические модели реальных ситуаций.
Деление многочленов".8кл.
|
Отметка | «3» | «4» | «5» |
| 3 задания | 4-5заданий | 6-7 заданий |
 Вариант 2
Вариант 2
Контрольная работа по алгебре №7
по теме: "Обобщение и систематизация знаний учащихся".8кл.
|
Отметка | «3» | «4» | «5» |
| 3 задания | 4-5 заданий | 6-7 заданий |
Вариант I

Контрольная работа по алгебре №7
по теме: "Обобщение и систематизация знаний учащихся".8кл.
|
Отметка | «3» | «4» | «5» |
| 3 задания | 4-5 заданий | 6-7 заданий |
 Вариант 2
Вариант 2






 дминистрация г. Улан-Удэ
дминистрация г. Улан-Удэ








 Вариант 2
Вариант 2
 Вариант 2
Вариант 2
 Вариант 2
Вариант 2









