Дополнительная общеразвивающая
общеобразовательная программа
с профориентационным модулем
естественно-научной направленности
кружка по математике
«ТРИОЗ: Теория решения исследовательских
и олимпиадных заданий»
I. Пояснительная записка
Дополнительная общеобразовательная (развивающая) программа кружка «ТРИОЗ» разработана в соответствии с идеей реализации методов формирования у учащихся 9 класса умений и навыков для решения исследовательских и олимпиадных заданий, усвоения дополнительных сведений, идей и подходов в этой области, а также содержит профориентационный профиль.
Актуальность:
Состояние математической подготовки учащихся характеризуется в первую очередь умением решать задачи. С другой стороны, задачи – это основное средство формирования системы основных математических знаний, умений и навыков, развития математического мышления и ведущей формой учебной деятельности учащихся в процессе обучения математике.
«Между работой ученика, решающего задачу по алгебре или геометрии, и изобретательской работой разница лишь в уровне, в качестве, так как обе работы аналогичного характера» − сказал однажды Ж. Адамар. А один из самых замечательных советских математиков – Б.Н. Делоне, − считал, что научное открытие отличается от хорошей олимпиадной задачи только тем, что для решения олимпиадной задачи требуется 5 часов, а для получения крупного научного результата требует затраты 5000 часов.
Каждому человеку природой даровано стремление к познанию и исследованию окружающего мира. Чтобы это стремление со временем не угасало, а, напротив, приобретало характер устойчивого желания, нужно упражняться в выполнении специальных заданий поисково-исследовательского характера.
Формирование у учащихся исследовательских умений является необходимым условием достижения развивающих и воспитательных целей математического образования. Исследовательская деятельность учащихся, индивидуальная или групповая, предусматривает не просто достижение того или иного результата, а организацию процесса достижения этого результата.
Профориентационный модуль программы «ТРИОЗ» связан с выбором профессии в рамках освоения программы, для формирования перспективных навыков и самоопределения в мире специальностей и направлений дальнейшего обучения учителя, программиста, финансиста, экономиста, аналитика, штурмана, инженера и др.
Профессиональное самоопределение личности - сложный и длительный процесс, охватывающий значительный период жизни. Его эффективность, как правило, определяется степенью согласованности психологических возможностей человека с содержанием и требованиями профессиональной деятельности, в связи с устройством своей профессиональной карьеры.
Результатом процесса профессионального самоопределения в старшем школьном возрасте является выбор будущей профессии. Помощь учащимся в правильном выборе профессии предполагает необходимость получение знаний о себе и о мире профессионального труда.
Целью исследовательской деятельности учащихся является не просто усвоение содержания, а решение определенной проблемы на основе этого содержания, т.е. активное применение получаемых знаний либо для получения нового знания, либо для получения практического результата на основе применения полученного знания. Математическая задача, являясь важнейшим средством формирования у школьников умения мыслить самостоятельно, развивает творческие способности учащихся, а значит, создает предпосылки для математического творчества – созидания математического знания.
Одной из форм творческой деятельности является исследовательская деятельность, поэтому ее следует рассматривать в качестве составной части проблемы развития творческих способностей учащихся.
Эффективность исследовательской деятельности учащихся зависит не только от меры увлеченности ею, но и от умения ее выполнять. Чтобы вкус к исследованиям не угасал, а лишь усиливался целесообразно придавать поисковой деятельности индуктивный характер, повторяя при этом путь естественного создания математического знания, наиболее соответствующий психике ребенка и подростка. Важно так вести учебное познание, чтобы вместе с маленькими находками или большими открытиями усваивалась бы и сама процедура исследования, как результат последовательного прохождения всех основных его этапов:
● мотивации исследовательской деятельности;
● постановки проблемы;
● сбора фактического материала;
● систематизации и анализа полученного материала;
● выдвижения гипотез;
● проверки гипотез;
● доказательства или опровержение гипотез.
Для практической реализации каждого из названных этапов нужны простые, доступные и удобные средства.
Мотивация исследовательской деятельности. Мотивирующая (исходная) задача должна обеспечить «видение» более общей проблемы, нежели та, которая отражена в ее условии.
Постановка проблемы. На первых порах для учащихся это весьма затруднительно, поэтому необходим контроль за выполнением задания, в дальнейшем учащиеся должны формулировать проблему самостоятельно.
Сбор фактического материала. Пробы (испытания) не должны быть лишены какой-либо логики. На первых порах необходимо задавать их направление посредством указаний, чертежей, пояснений и т.п. Число испытаний не следует строго ограничивать, оно должно быть достаточным для получения необходимого фактического материала.
Систематизацию и анализ полученного материала полезно осуществлять с помощью удобных таблиц, диаграмм, схем, графиков и т.п., они позволят визуально определить необходимые свойства, связи, соотношения, закономерности.
Выдвижение гипотез. Очень важно научиться записывать гипотезы на математическом языке, это придает им точность и лаконичность, не следует ограничивать число возможных гипотез.
Проверка гипотез. Чаше всего проверку гипотез целесообразно осуществлять посредством проведения еще одного испытания. При этом результат новой пробы сопоставляется со значениями, полученными на основе гипотез.
На последнем этапе проводится доказательство истинности гипотез, получивших ранее подтверждение или уточнение; ложность же их может быть определена с помощью контрпримеров. В начале работы с учащимися важно уметь пользоваться эвристиками (подсказками): это может быть схематическое изображение проблемной ситуации, чертеж с особыми пометками, подсказывающими идею доказательства и др. Идея доказательства может зародиться в процессе выполнения испытаний, может возникнуть и при анализе систематизированного фактического материала, и на ней следует акцентировать свое внимание. Важно отметить также, что в ряде случаев бывает проще установить равносильность двух или более гипотез и доказать одну из них, нежели искать доказательства для каждой гипотезы в отдельности.
Данная схема подтвердила свою эффективность при использовании ее в исследовательских картах по математике М.И. Зайкина и Е.В. Барановой.
Программа математического кружка предусматривает изучение отдельных вопросов, непосредственно примыкающих к основному курсу и углубляющих его через включение более сложных задач исследовательского характера при минимальном расширении теоретического материала. Программа предусматривает доступность излагаемого материала для учащихся и планомерное развитие их интереса к предмету. Учебно-тематический план включает теоретические и практические задания.
Изучение математики на ступени основного общего образования направлено на достижение следующих целей:
● овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
● интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
● формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
● воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
Основной целью работы кружка является создание системы интеллектуального развития лицеистов средствами математики.
Достижение этой цели возможно при решении следующих задач:
● углубление и расширение знаний обучающихся по математике;
● развитие математического кругозора, мышления, исследовательских умений учащихся;
● формирование у обучающихся опыта творческой деятельности;
● воспитание у школьников настойчивости, инициативы, самостоятельности.
● формировать особые качества ума (критичность, гибкость, доказательность и др.) через систему развивающих игр и творческих заданий по математике;
● создавать условия для формирования и развития практических умений учащихся решать нестандартные задачи, используя различные методы и приемы.
Целью профориентационного модуля является актуализация процесса профессионального самоопределения учащихся за счет специальной организации их деятельности, включающей получение знаний о себе, о мире профессионального труда.
Достижение этой цели возможно при решении следующих задач:
повышение уровня психологической компетенции учащихся за счет вооружения их соответствующими знаниями и умениями
формирование положительного отношения к самому себе, создание своей индивидуальности, уверенность в своих силах применительно к реализации себя в будущей профессии;
обеспечение возможности соотносить свои склонности и способности с требованиями профессиональной деятельности с помощью включения их в систему специально организованных профессиональных проб.
Возраст детей, участвующих
в реализации данной программы
В математический кружок «ТРИОЗ» принимаются обучающиеся 14−15 лет (9 класс), интересующиеся математикой. Наполняемость кружка – 12 человек. Занятия проводятся еженедельно в классных комнатах. Результаты обучения оцениваются через математические олимпиады, математические соревнования и игры. Срок реализации программы – 1 год.
Формы и методы организации занятий
Основными формами образовательного процесса являются:
● решение нестандартных и олимпиадных задач исследовательского характера;
● математические тренинги;
● математические конкурсы, игры, соревнования;
● математические олимпиады.
На занятиях предусматриваются следующие формы организации учебной деятельности:
● индивидуальная (воспитаннику даётся самостоятельное задание с учетом его возможностей);
● фронтальная (работа в коллективе при объяснении нового материала или отработке определенной темы);
● групповая (разделение на минигруппы для выполнения определённой работы);
● коллективная (выполнение работы для подготовки к олимпиадам, конкурсам).
Методической основой программы является математическое содержание и математические знания развивающего характера. В его основу положен продуктивно - деятельностный подход (М.И. Зайкин) к обучению математике обучающихся, способствующий формированию исследовательских и творческих умений учащихся.
Обучающихся ориентируют на участие во всевозможных математических конкурсах (Интернет-карусель, Авангард, Познание и творчество), Всероссийской олимпиаде школьников по математике и в Международном математическом конкурсе «Кенгуру».
Основные виды продуктивной
математической деятельности учащихся:
● знакомство с научно-популярной литературой, связанной с математикой;
● решение нестандартных и олимпиадных математических задач, исследовательского характера;
● решение задач несколькими способами;
● составление (видоизменение) математических задач;
● участие в математических конкурсах и олимпиадах, международной конкурсе «Кенгуру»;
● самостоятельная работа учащихся;
● творческие математические работы.
Требования к уровню подготовки обучающихся
В результате изучения программы кружка ученик должен:
знать/понимать
● существо понятия алгоритма; примеры алгоритмов;
● как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
● как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
● как потребности практики привели математическую науку к необходимости расширения понятия числа;
● смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
уметь
● составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
● выполнять основные действия с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
● применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
● решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;
● решать линейные и квадратные неравенства с одной переменной и их системы;
● определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
● находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
● определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
● описывать свойства изученных функций, строить их графики;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
● выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
● моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;
● описания зависимостей между физическими величинами, соответствующими формулами при исследовании несложных практических ситуаций;
● интерпретации графиков реальных зависимостей между величинами.
Критерии оценок результатов итоговой
(промежуточной аттестации)
Критерии оценки уровня теоретической подготовки обучающихся:
● соответствие уровня теоретических знаний программным требованиям;
● широта кругозора;
● осмысленность и свобода использования специальной терминологии;
Критерии оценки уровня практической подготовки обучающихся:
● соответствие уровня развития практических умений и навыков программным требованиям;
● качество выполнения практического задания;
● технологичность практической деятельности;
Критерии оценки уровня развития и воспитанности обучающихся:
● культура поведения;
● творческое отношение к выполнению практического задания;
● аккуратность и ответственность в работе;
● развитость математических способностей.
Оценка аттестации
Для оценки усвоения обучающимися содержания образовательной программы кружка применяется следующая система оценивания:
минимальный уровень − учащийся решает типовые задачи по алгоритму, знает и понимает существо понятия алгоритма; примеры алгоритмов; как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
базовый уровень − учащийся решает типовые (алгоритмические) задачи и задачи повышенной трудности (выход из алгоритма решения задачи), знает и понимает основные методы решения олимпиадных математических и практических задач;
повышенный уровень − знает и понимает основные методы решения олимпиадных математических и практических задач, решает задачи повышенной трудности и нестандартные задачи; умеет объяснять, как получен результат данного выражения; понимает и применяет на практике математическую информацию из области содержания; использует приобретенные знания и умения в практической деятельности и повседневной жизни.
Аттестация обучающихся проводится два раза в год: промежуточная в декабре – январе, итоговая в мае.
Форма проведения итоговой аттестации: самостоятельные учебно-исследовательские работы учащихся, математическое домино.
II. Содержание рабочей программы
Последовательности (8 часов)
Понятие числовых последовательностей, многообразие числовых последовательностей. последовательность Фиббоначи. Закономерности в числовых последовательностях. Способы задания числовых последовательностей (словесное задание, по формуле 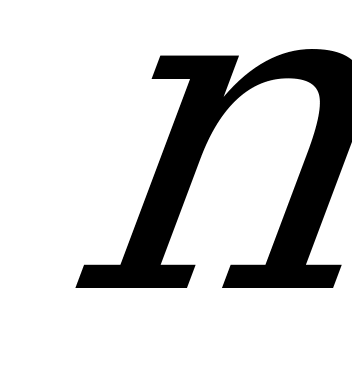 -ого члена, рекуррентное задание). Арифметическая прогрессия, формула нахождения суммы
-ого члена, рекуррентное задание). Арифметическая прогрессия, формула нахождения суммы 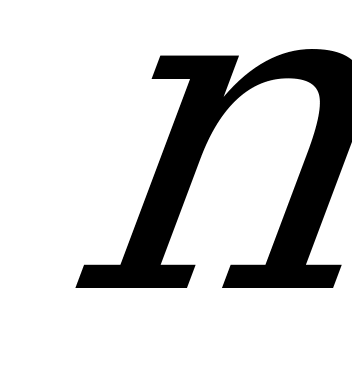 членов арифметической прогрессии. Решение олимпиадных задач, связанных с арифметической прогрессией.
членов арифметической прогрессии. Решение олимпиадных задач, связанных с арифметической прогрессией.
Индуктивные исследования (13 часов)
Рассмотрение индуктивных исследований, предполагающих обобщение частных случаев. В данном разделе учащиеся совместно с педагогом исследуют зависимости между количеством геометрических элементов, изображенных на плоскости и числом частей плоскости, получаемых в результате. Также исследуется зависимость между количеством диагоналей выпуклого многоугольника и числа его вершин. В завершении раздела рассматриваются олимпиадные задачи, которые решаются сведению к рассмотрению частных случаев и последующему обобщению результатов.
Алгебраические исследования (9 часов)
В данном разделе рассматриваются различные алгебраические задания и примеры, которые обобщаются и доказываются. В частности, при сокращении обыкновенных дробей пользуются известным свойством: если числитель и знаменатель дроби разделить на их общий делитель, то получится равная ей дробь. однако в некоторых случаях сокращение можно выполнять не по этому правилу, а иначе, просто зачеркивая у них дробные части, оставляя неизменными целые части, или иногда даже вычеркиванием одной или нескольких цифр из числа. такие частные случаи сокращения "не по правилам" предлагается исследовать учащимся.
Исследование иррациональностей (8 часов)
Извлечение корня из числа называют седьмой операцией над числами (после счета (нумерации), сложения, вычитания, умножения, деления и возведения в степень). От всех остальных операций она отличается одной важной характеристикой , не всегда выполняется. Рассматривается выведенная И. Ньютоном формула преобразования сложных радикалов. Учащиеся совместно с педагогом исследуют применение формулы сложных радикалов для преобразования иррационального выражения в натуральное число, или сумму (разность) натурального числа и корня. В данном разделе рассматривается также случай обобщения и оценки бесконечного числа цепных квадратных корней.
III. Учебно-тематический план
| № | Тема | Количество часов |
| теория | практика |
| 1 | Последовательности | 2 | 5 |
| 2 | Индуктивные исследования | 6 | 7 |
| 3 | Алгебраические исследования | 4 | 5 |
| 4 | Исследование иррациональностей | 5 | 3 |
|
| Итого: | 18 | 20 |
|
| Всего: | 38 |
IV. Календарно-тематическое планирование
Кружок «ТРИОЗ», 9 класс
| № | Дата прове-дения |
Тема | Теория | Пракика |
| Последовательности (8 часов) |
| 1 |
| Применение навыков решения исследовательских и олимпиадных задач при выборе престижных и востребованных профессий. Числовые последовательности | 1 | 1 |
| 2 |
| Способы записи числовых последовательностей | 0 | 1 |
| 3 |
| Арифметическая прогрессия | 1 | 1 |
| 4 |
| Сумма 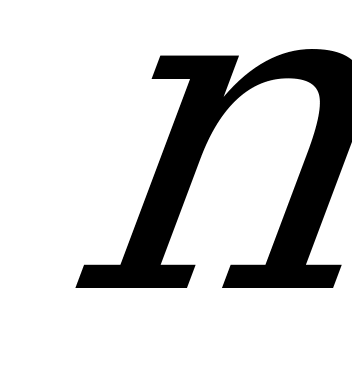 членов арифметической прогрессии членов арифметической прогрессии | 1 | 1 |
| 5 |
| Математический тренинг по изученным темам | 0 | 1 |
| итого | 3 | 5 |
| Индуктивные исследования (13 часов) |
| 36 |
| Разбиение прямой точками на отрезки | 1 | 1 |
| 7 |
| Разбиение угла лучами | 1 | 1 |
| 8 |
| Диагонали выпуклого четырехугольника | 1 | 1 |
| 9 |
| Разбиение плоскости на части прямыми. Практикум по решению задач. | 1 | 1 |
| 10 |
| Разбиение плоскости на части окружностями | 1 | 1 |
| 11 |
| Разбиение плоскости на части углами | 1 | 1 |
| 12 |
| Промежуточная аттестация. Практикум по решению олимпиадных задач. | 0 | 1 |
| итого | 6 | 7 |
| Алгебраические исследования (9 часов) |
| 13 |
| Возможности получения образования по инженерным специальностям. "Счастливый" билет | 1 | 0 |
| 14 |
| Признаки делимости на 9, 99, 999, ... | 1 | 1 |
| 15 |
| Признаки делимости на 2, 4, 8, ..., 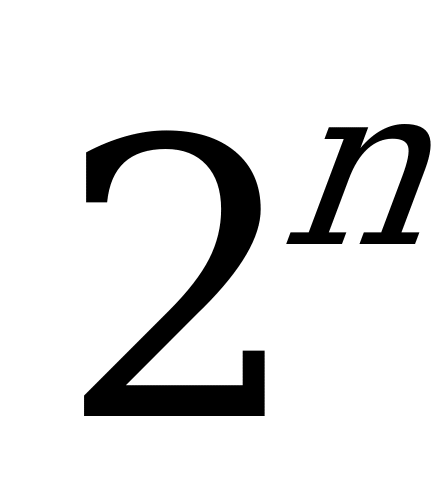 | 1 | 1 |
| 16 |
| Признаки делимости на 5, 25, ..., 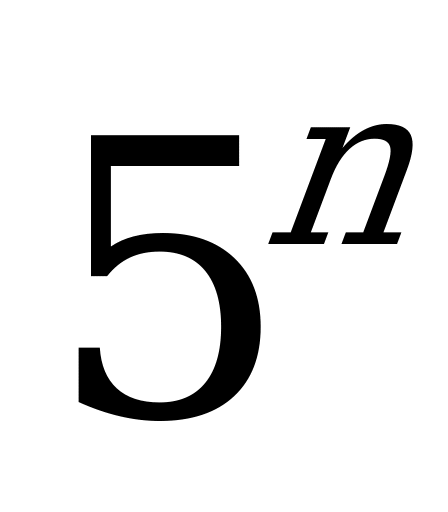 | 1 | 1 |
| 17 |
| Решение олимпиадных задач | 0 | 1 |
| 18 |
| Сокращения не по правилам | 0 | 1 |
| итого | 4 | 5 |
| Исследование иррациональностей (8 часов) |
| 19 |
| Из истории формулы сложных радикалов | 1 | 0 |
| 20 |
| Преобразование сложных радикалов в натуральное число | 0 | 1 |
| 21 |
| Преобразование суммы (разности) сопряженных сложных радикалов в натуральное число | 1 | 1 |
| 22 |
| Индуктивное обобщение | 1 | 0 |
| 23 |
| Творческие отчеты учащихся | 1 | 0 |
| 24 |
| Итоговая аттестация. Математическое домино | 0 | 1 |
| 25 |
| Развитие первоначальных профессиональных навыков в программировании при решении исследовательских и олимпиадных задач | 1 | 0 |
| итого | 5 | 3 |
|
| Всего за год | 18 | 20 |
| Всего за год | 38 |
V. Методическое обеспечение программы
Для успешной реализации данной программы используются современные методы и формы занятий, которые помогают сформировать у обучающихся устойчивый интерес к данному виду деятельности:
Словесные методы: рассказ, беседа, объяснение, работа с книгой, метод примера.
Наглядные методы: просмотр журналов, схем, плакатов, рисунков.
Практические методы: работа в группах, индивидуальная работа, практикумы, исследовательская работа, игры.
Методы стимулирования и мотивации: формирование опыта эмоционально-ценностных отношений у обучающихся; интереса к деятельности и позитивному поведению, долга и ответственности.
Методы создания положительной мотивации обучаемых:
Эмоциональные: ситуация успеха, поощрение и порицание, познавательная игра, свободный выбор задания, удовлетворение желание быть значимой личностью.
Волевые: предъявление образовательных требований, формирование ответственного отношения к получению знаний; информирование о прогнозируемых результатах образования.
Социальные: развитие желания быть полезным обществу, создание ситуации взаимопомощи и в результатах коллективной работы.
Познавательные: опора на субъективный опыт ребёнка, решение творческих задач, создание проблемной ситуации.
В основу всех форм учебных занятий заложены общие характеристики:
каждое занятие имеет цель, конкретное содержание, определённые методы организации учебно-педагогической деятельности;
любое занятие имеет определённую структуру, т. е. состоит из отдельных взаимосвязанных этапов;
построение учебного занятия осуществляется по определённой логике, когда тип занятия соответствует его цели и задачам.
Основная форма обучения – комплексное учебное занятие, включающее в себя вопросы теории и практики.
Подготовка по тематическому принципу, соблюдая «правила спирали» от простых типов заданий до заданий более сложных. Работа с такими видами заданий, выстроенными в виде логически взаимосвязанной системы, где из одного вытекает другое, т.е. правильно решенное предыдущее задание готовит понимание смысла следующего; выполненное сегодня задание готовит к пониманию и правильному выполнению завтрашнего и т. д.
Максимальное использование наличного запаса знаний, применяя различные «хитрости» и «правдоподобные рассуждения», для получения ответа простым и быстрым способом.
Для реализации данной программы необходимы следующие комплексы:
Методические комплексы, состоящие из информационного материала и конспектов; технологических и инструкционных карт; методических разработок и планов конспектов занятий.
Дидактические материалы: таблицы, схемы, плакаты, дидактические карточки, памятки, научная и специальная литература, раздаточный материал, мультимедийные материалы, компьютерные программные средств (продукция компаний «Кирилл и Мефодий», "Просвещение - МЕДИА", «Физикон», «Новый Диск», по мере необходимости.
Техническое и материальное оснащение. компьютер, мультимедийный проектор с экраном, справочные пособия (энциклопедии, словари, сборники основных формул и т.п.).
10
















