Муниципальное автономное общеобразовательное учреждение
«Средняя общеобразовательная школа № 1»
города Покачи Ханты-Мансийского автономного округа-Югры
| Рекомендовано: Предметной комиссией
протокол от _________ №__
__________ _____________ Подпись ФИО
| Согласовано: Заместитель директора по УР ______________________ дата
_________ _____________ Подпись ФИО | Утверждено: Приказ от __________ № ___
Директор МАОУ СОШ №1
_________ _____________ Подпись ФИО
|
РАБОЧАЯ ПРОГРАММА
учебного предмета «Математика (профильный уровень)»
для 11 «А», «Б» классов
210 часов (6 часа в неделю)
| Составитель рабочей программы: _Кузнецова Ольга Федоровна ФИО Квалификационная категория первая |
2019 – 2020 учебный год
Рабочая программа профильного уровня составлена на основе:
Федеральный закон Российской Федерации от 29 декабря 2012 г. N 273-ФЗ «Об образовании в Российской Федерации»;
Постановление Главного санитарного врача РФ от 29.12. 2010г. № 189 «Об утверждении СанПиН 2.4.2.2821-10 «Санитарно-эпидемиологические требования к условиям и организации обучения в общеобразовательных учреждениях»; Приказ Министерства образования и науки РФ от 06.10.2009 г. № 373 «Об утверждении и введении в действие федерального государственного образовательного стандарта начального общего образования»; Приказ Министерства образования и науки РФ от 17.12.2010 г. № 1897 «Об утверждении и введении в действие федерального государственного образовательного стандарта основного общего образования»; Приказ Минобразования России от 05.03.2004 №1089 "Об утверждении федерального компонента государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования"; - Приказ Минобрнауки России от 31.03.2014 № 253 "Об утверждении федерального перечня учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования"; Приказ Минобрнауки России от 30.08.2013 № 1015 «Об утверждении Порядка организации и осуществления образовательной деятельности по основным общеобразовательным программам – образовательным программам начального общего, основного общего и среднего общего образования»; Устав МАОУ СОШ №1; Приказ МАОУ СОШ № 1 от 31 .05.2019 г. № 321/1-О «Об внесении изменений основной образовательной программы НОО, ООО, СОО муниципального автономного общеобразовательного учреждения «Средняя общеобразовательная школа №1» на 2019-2020 учебный год»;
Приказ МАОУ СОШ № 1 от 12 мая 2016 г. № 276-О «Об утверждении положения о рабочей программе учебного предмета, курса муниципального автономного общеобразовательного учреждения «Средняя общеобразовательная школа №1». сборник программ основной общеобразовательной школы ( автор – составитель Т.А. Бурмистрова) М.: Просвещение, 2016; рабочая программа по предмету «Геометрия»: (авторы: Л.С. Атанасян, С.М.Кадамцев и др ). Москва. Просвещение, 2016г.;
В соответствие с учебным планом школы на изучение математики на профильном уровне в 11 классе отводится не менее 204 часов, из расчёта 6 часов в неделю. Курс математики 11 класса состоит из следующих предметов: «Алгебра и начала анализа», «Геометрия», которые изучаются блоками. В соответствии с этим составлено тематическое планирование: алгебра и начала анализа из расчета 4 часа в неделю, геометрия – 2 часа в неделю. Контрольных работ за год – 12.
Содержание курса полностью соответствует примерной программе, на основании которой составлена рабочая программа. Внесены изменения: тема «Векторы» была изучена в 10 классе, поэтому освободившиеся часы распределены по темам курса геометрии: добавлено по 3 часа на темы: «Цилиндр, конус, шар», «Объемы тел».
Рабочая программа ориентирована на преподавание алгебраического материала по учебнику «Алгебра и начала математического анализа» 11класс под редакцией С.М. Никольского серии «МГУ-школе», Москва «Просвещение», 2009; геометрического материала по учебнику «Геометрия» 10-11 кл. под редакцией Л.С.Атанасяна, В.Ф. Бутузова, С.Б. Кадомцева и др. – М.: Просвещение, 2011, входящих в федеральный перечень учебников, рекомендованных (допущенных) к использованию в образовательном процессе Министерством образования и науки РФ на 2013/2014 учебный год.
УМК по алгебре и началам математического анализа включает:
Алгебра и начала математического анализа. 11 класс: учебник/С.М.Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин. М.: Просвещение, 2009
Алгебра и начала математического анализа. Дидактические материалы. 11 класс/ М. К. Потапов, А.В. Шевкин. М.: Просвещение, 2010.
Алгебра и начала математического анализа. Тематические тесты. 11 класс/П.В. Чулков, Т.С. Струков. М.: Просвещение, 2010.
УМК по геометрии включает:
1. Геометрия.10-11 класс: учебник/Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Л.С. Киселев, Э.Г. Позняк. М.: Просвещение, 2011
2. Геометрия. Дидактические материалы. 11 класс./Б.Г. Зив. М.: Просвещение,2011
3. Зив Б.Г. и др. Задачи по геометрии для 7-11 классов / М.: Просвещение, 2009.
4. Бутузов В.Ф., Глазков Ю.А., Юдина И.И. Рабочая тетрадь по геометрии для 11 класса / М.:Просвещение,2013.
1.1.Основная цель математики 11 класса в системе общего образования
формирование представлений об идеях и методах математики; о математике как универсальном языке науки, средстве моделирования явлений и процессов;
овладение устным и письменным математическим языком, математическими знаниями и умениями, необходимыми для изучения школьных естественно - научных дисциплин, для продолжения образования и освоения избранной специальности на современном уровне;
развитие логического мышления, алгоритмической культуры, пространственного воображения, развитие математического мышления и интуиции, творческих способностей на уровне, необходимом для продолжения образования и для самостоятельной деятельности в области математики и ее приложений в будущей профессиональной деятельности;
воспитание средствами математики культуры личности: знакомство с историей развития математики, эволюцией математических идей, понимание значимости математики для общественного прогресса.
1.2. Изучение математики 11 класса в основной школе должно обеспечить:
уровневую дифференциацию в ходе обучения;
базу математических знаний, достаточную для изучения алгебры и геометрии, а также для продолжения образования;
сформировать устойчивый интерес учащихся к предмету;
выявить и развить математические и творческие способности;
Владеть компетенциями:
1.3. Общая характеристика учебного предмета:
Специфика целей и содержания изучения алгебры и начал анализа на профильном уровне существенно повышает требования к рефлексивной деятельности учащихся: к объективному оцениванию своих учебных достижений, поведения, черт своей личности, способности и готовности учитывать мнения других людей при определении собственной позиции и самооценке, понимать ценность образования как средства развития культуры личности. В течение года возможны коррективы рабочей программы, связанные с объективными причинами. В современных условиях образование призвано обеспечить функциональную грамотность и социальную адаптацию обучающихся на основе приобретения ими компетентностного опыта в сфере учения, познания, профессионально-трудового выбора, личностного развития, ценностных ориентаций и смыслотворчества. Это предопределяет направленность целей обучения на формирование компетентной личности, способной к жизнедеятельности и самоопределению в информационном обществе, ясно представляющей свои потенциальные возможности, ресурсы и способы реализации выбранного жизненного пути.
Результаты обучения математике 11 класс
Личностными результатами обучения
Формирование ответственного отношения к учению, готовности и способности к саморазвитию и самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего образования на базе ориентировки в мире профессий и профессиональных предпочтений, осознанному построению индивидуальной образовательной траектории с учетом устойчивых познавательных интересов.
Формирование целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики.
Формирование коммуникативной компетентности в общении и сотрудничестве со сверстниками, старшими и младшими в образовательной, общественно полезной, учебно-исследовательской, творческой и других видах деятельности.
Умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры.
Критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
Креативность мышления, инициатива, находчивость, активность при решении геометрических задач.
Умение контролировать процесс и результат учебной математической деятельности.
Способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
Метапредметные результаты
Умение самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
Умение осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необхлдимые коррективы;
Умение адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения;
Осознанное владение логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев;
Умение устанавливать причинно-следственные связи, строить логические рассуждения, умозаключения, выводы;
Умение создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач;
Умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников, общие способы работы; умение работать в группе; слушать партнера; формулировать, аргументировать и отстаивать свое мнение;
Формирование и развитие учебной и общепользовательской компетентности в области использования информационно коммуникационных технологий;
Первоначальные представления об идеях и методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
Умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей среде;
Умение находить в различных источниках информацию, необходимую для решения математических проблем , представлять ее в понятной форме, принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
Умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы) для иллюстрации, интерпретации, аргументации;
Умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
Понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
Умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения проблем;
Умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
Предметные результаты
овладение базовым понятийным аппаратом по основным разделам содержания; представление об основных изучаемых понятиях как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления;
умение работать с геометрическим текстом, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, проводить классификации, логические обоснования, доказательства математических утверждений;
овладение навыками устных, письменных, инструментальных вычислений;
овладение геометрическим языком, умение использовать его для описания предметов окружающего мира, развитие пространственных представлений;
усвоение систематических знаний о плоских фигурах, а также на наглядном уровне – о простейших пространственных телах, умение применять систематические знания о них для решения геометрических и практических задач;
умение измерять длины отрезков, величины углов, использовать формулы для нахождения периметров, площадей и объемов геометрических фигур;
умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием справочных материалов, калькулятора, компьютера.
Содержание разделов курса
Алгебра
11 класс
Функции и их графики.
Элементарные функции. Исследование функций и построение их графиков элементарными методами. Основные способы преобразования графиков. Графики функций, содержащих модули. Графики сложных функций.
О с н о в н а я ц е л ь – овладеть методами исследования функций и построения графиков.
Сначала вводятся понятия элементарной функции и суперпозиции функций (сложной функции). Затем исследуются вопросы об области определения и области изменения функции, об ограниченности, четности ( или нечетности) и периодичности функции, о промежутках возрастания ( убывания) знакопостоянства функции. Результаты исследования функции применяются для построения ее графика. Далее рассматриваются основные способы преобразования графиков функций – симметрия относительно осей координат, сдвиг вдоль осей, растяжение графиков.. Все эти способы применяются к построению графиков функции  по графику функции
по графику функции  .
.
Рассматривается симметрия графиков функций  и
и  относительно прямой
относительно прямой  . По графику функции
. По графику функции  строятся графики функций
строятся графики функций  и
и 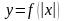 . Затем строятся графики функций, являющихся суперпозицией, суммой, произведением. функций.
. Затем строятся графики функций, являющихся суперпозицией, суммой, произведением. функций.
Предел функции и непрерывность.
Понятие предела функции. Односторонние пределы, свойства пределов. Непрерывность функций в точке, на интервале, на отрезке. Непрерывность элементарных функций. Разрывные функции.
О с н о в н а я ц е л ь – усвоить понятия предела функции и непрерывности функции в точке и на интервале.
На интуитивной основе вводятся понятия предела функции сначала при  ,
,  , затем в точке. Рассматриваются односторонние пределы и свойства пределов функций. Вводится функций. Вводится понятие непрерывности функции в точке и на интервале. Выясняются промежутки непрерывности элементарных функций.
, затем в точке. Рассматриваются односторонние пределы и свойства пределов функций. Вводится функций. Вводится понятие непрерывности функции в точке и на интервале. Выясняются промежутки непрерывности элементарных функций.
Вводится понятие непрерывности функции справа ( слева ) в точке  и непрерывности функции на отрезке. Приводится также определение предела функции в точке «на языке
и непрерывности функции на отрезке. Приводится также определение предела функции в точке «на языке » и «на языке последовательностей». Вводится понятие разрывной функции и рассматриваются примеры разрывных функций.
» и «на языке последовательностей». Вводится понятие разрывной функции и рассматриваются примеры разрывных функций.
Обратные функции.
Понятие обратной функции. Взаимно обратные функции. Обратные тригонометрические функции.
О с н о в н а я ц е л ь – усвоить понятие функции, обратной к данной, и научить находить функцию, обратную к данной.
Сначала на простом примере вводится понятие функции, обратной к данной. Затем определяется функция, обратная к данной строго монотонной функции. Приводится способ построения графика обратной функции.
Вводится понятие взаимно обратных функций, устанавливается свойство графиков взаимно обратных функций, построенных в одной системе координат. Исследуются основные обратные тригонометрические функции и строятся их графики.
Производная.
Понятие производной. Производная суммы, разности, произведения и частного двух функций. Непрерывность функций, имеющих производную, дифференциал. Производные элементарных функций. Производная сложной функции. Производная обратной функции.
О с н о в н а я ц е л ь – научить находить производную любой элементарной функции.
Сначала вводится новая операция: дифференцирование функции и ее результат – производная функции. Затем выясняется механический и геометрический смысл производной, после чего находятся производные суммы, разности, произведения, честного и суперпозиции двух функций, а так же производные всех элементарных функций. Доказывается непрерывность функции в точке, в которой она имеет производную. Вводится понятие дифференциала функции, доказывается теорема о производной обратной функции и находятся производные для обратных тригонометрических функций.
Применение производной.
Максимум и минимум функции. Уравнение касательной. Приближенные вычисления. Теоремы о среднем. Возрастание и убывание функций. Производные высших порядков. Выпуклость графика функции. Экстремум функции с единственной критической точкой. Задачи на максимум и минимум. Асимптоты. Дробно-линейная функция. Построение графиков функций с применением производной. Формула и ряд Тейлора..
О с н о в н а я ц е л ь – научить применять производную при исследовании функций и решении практических задач.
Сначала вводятся понятия локальных максимума и минимума функции, ее критических точек, а затем рассматривается метод нахождения максимума и минимума функции на отрезке. Выводится уравнение касательной к графику функции, исследуется возрастание и убывание функции с помощью производных. Рассматриваются экстремум функции с единственной критической точкой и задачи на максимум и минимум. Проводится исследование функций с помощью производной, строятся их графики.
Доказываются теоремы Роля и Лагранжа. Обсуждается вопрос о выпуклости вверх ( или вниз) графика функции, имеющей вторую производную, т.е. вопрос о геометрическом смысле второй производной. Вводится понятие асимптоты графика функции. Исследуется дробно-линейная функция. Вводятся понятия формулы и ряда Тейлора, показывается их применение при приближенных вычислениях.
Первообразная и интеграл.
Понятие первообразной. Замена переменной и интегрирование по частям. Площадь криволинейной трапеции. Определенный интеграл. Приближенное вычисление определенного интеграла. Формула Ньютона-Лейбница. Свойства определенных интегралов. Применение определенных интегралов в геометрических и физических задачах. Понятие дифференциального уравнения. Задачи, приводящие к дифференциальным уравнениям.
О с н о в н а я ц е л ь – знать таблицу первообразных ( неопределенных интегралов ) основных функций и уметь применять формулу Ньютона-Лейбница при вычислении определенных интегралов и площадей фигур.
Сначала вводится понятие первообразной для функции, непрерывной на интервале, затем понятие неопределенного интеграла, приводятся основные свойства неопределенных интегралов и таблица неопределенных интегралов. Определяется площадь криволинейной трапеции как предел интегральной суммы для неотрицательной функции. Определенный интеграл также вводится как предел интегральной
Равносильность уравнений и неравенств.
Равносильные преобразования уравнений и неравенств.
О с н о в н а я ц е л ь – научить применять равносильные преобразования при решении уравнений инеравенств.
Сначала перечисляются равносильные преобразования уравнений. Подчеркивается, что при таких преобразованиях множество корней преобразованного уравнения совпадает с множеством корней исходного уравнения. Рассматриваются примеры применения таких преобразований при решении уравнений.
Затем аналогичным образом рассматриваются равносильные преобразования неравенств и их применение при решении неравенств.
Уравнения - следствия.
Понятие уравнения-следствия. Возведение уравнения в четную степень. Потенцирование логарифмических уравнений. Приведение подобных членов уравнения. Освобождение уравнения от знаменателя. Применение логарифмических, тригонометрических и других формул.
О с н о в н а я ц е л ь – научить применять преобразования, приводимые к уравнению-следствию.
Сначала вводится понятие уравнения-следствия, перечисляются преобразования, приводимые к уравнению-следствию. Подчеркивается, что при таком способе решения уравнения проверка корней уравнения-следствия является обязательным этапом решения исходного уравнения. Затем рассматриваются многочисленные примеры применения каждого из этих преобразований в отдельности и нескольких таких преобразований.
Равносильность уравнений и неравенств системам.
Решение уравнений с помощью систем. Уравнения вида  Решение неравенств с помощью систем. Неравенства вида
Решение неравенств с помощью систем. Неравенства вида 
О с н о в н а я ц е л ь – научить применять переход от уравнения ( или неравенства ) к равносильной системе.
Сначала вводится понятие системы, равносильности систем, равносильности уравнения ( неравенства ) системе или совокупности систем.
Затем перечисляются некоторые уравнения ( неравенства ) и равносильные им системы. Формулируются утверждения об их равносильности. Приводятся примеры применения этих утверждений.
Для уравнения вида  и неравенства вида
и неравенства вида  формулируются утверждения об их равносильности соответствующим системам.
формулируются утверждения об их равносильности соответствующим системам.
Равносильность уравнений на множествах.
Возведение уравнения в четную степень. Умножение уравнения на функцию. Логарифмирование и потенцирование уравнений, приведение подобных членов, применение некоторых формул.
О с н о в н а я ц е л ь – научить применять переход к уравнению, равносильному на некотором множестве исходному уравнению.
Сначала вводится понятие равносильности двух уравнений на множестве, описываются те множества чисел, на каждом из которых получается уравнение, равносильное на этом множестве исходному уравнению при возведении уравнения в четную степень, при умножении уравнения на функцию, при логарифмировании, при потенцировании, при приведении подобных членов уравнения, при применении некоторых формул. Для каждого преобразования уравнения формулируется соответствующие утверждения о равносильности и приводятся примеры их применения.
Равносильность неравенств на множествах.
Возведение неравенства в четную степень и умножение неравенства на функцию, потенцирование логарифмических неравенств, приведение подобных членов, применение некоторых формул. Нестрогие неравенства.
О с н о в н а я ц е л ь – научить применять переход к неравенству, равносильному на некотором множестве исхожному неравенству.
Вводится понятие равносильности двух неравенств на множестве, описываются те множества чисел, на каждом из которых получается неравенство, равносильное на этом множестве исходному неравенству при возведении уравнения в четную степень, при умножении уравнения на функцию, при потенцировании логарифмического неравенства, при приведении подобных членов неравенства, при применении некоторых формул. Для каждого преобразования неравенства формулируются соответствующие утверждения о равносильности и приводятся примеры их применения. Рассматриваются нестрогие неравенства.
Метод промежутков для уравнений и неравенств.
Уравнения и неравенства с модулями. Метод интервалов для непрерывных функций.
О с н о в н а я ц е л ь – научить решать уравнения и неравенства с модулями и применять метод интервалов для решения неравенств.
Сначала рассматриваются уравнения с модулями и описывается способ решения таких уравнений переходом к уравнениям, равносильным исходному на некотором множестве и не содержащем модулей. Затем аналогично рассматриваются неравенства с модулями. Наконец, для функций  , непрерывных на некоторых интервалах, рассматривается способ решения неравенств
, непрерывных на некоторых интервалах, рассматривается способ решения неравенств  и
и  , называемый методом интервалов.
, называемый методом интервалов.
При обучении на профильном уровне рассматриваются более сложные уравнения и неравенства.
Использование свойств функций при решении уравнений и неравенств.
Использование областей существования, неотрицательности, ограниченности, монотонности и экстремумом функции, свойств синуса и косинуса при решении уравнений и неравенств.
О с н о в н а я ц е л ь – научить применять свойства функций при решении уравнений и неравенств.
Приводятся примеры решения уравнений и неравенств с использованием свойств функций.
Системы уравнений с несколькими неизвестными.
Равносильность систем. Система-следствие. Метод замены неизвестных. Рассуждения с числовыми значениями при решении систем уравнений.
О с н о в н а я ц е л ь – освоить разные способы решения систем уравнений с несколькими неизвестными.
Вводятся понятия системы уравнений, равносильности систем, приводятся утверждения о равносильности систем при тех или иных преобразованиях, рассматриваются основные методы решения систем уравнений: метод подстановки, метод линейных преобразований, метод перехода к системе-следствию, метод замены неизвестных.
Рассматриваются решение систем уравнений при помощи рассуждений с числовыми значениями.
Повторение курса алгебры и начал математического анализа за 10-11 классы.
Геометрия
11 класс
( 2 часа в неделю, всего 68 часов)
Метод координат в пространстве.
Координаты точки и координаты вектора . Скалярное произведение векторов. Движение..
О с н о в н а я ц е л ь – сформировать умения применять координатный и векторный методы к решению задач на нахождение длин отрезков и углов между прямыми и векторами в пространстве.
В ходе изучения темы целесообразно использовать аналогию между рассматриваемыми понятиями на плоскости и в пространстве. Это поможет учащимся более глубоко о осознанно усвоить изучаемый материал, уяснить содержание и место векторного и координатного методов в курсе геометрии.
Цилиндр, конус, шар.
Цилиндр. Площадь поверхности цилиндра. Конус. Площадь поверхности конуса. Усеченный конус. Сфера. Шар. Взаимное расположение сферы и плоскости. Касательная плоскость к сфере. Площадь сферы.
О с н о в н а я ц е л ь – дать учащимся систематические сведения об основных видах тел вращения.
Изучение круглых тел (цилиндра, конуса, шара ) завершает изучение системы основных пространственных геометрических тел.
В ходе знакомства с теоретическим материалом темы значительно развиваются пространственные представления учащихся: круглые тела рассматриваются на примере конкретных геометрических тел, изучается взаимное расположение круглых тел и плоскостей ( касательные и секущие плоскости), происходит знакомство с понятиями описанных и вписанных призм и пирамид.
Решается большое количество задач, что позволяет продолжить формирование логических и графических умений.
Объемы тел.
Объем прямоугольного параллелепипеда. Объемы прямой призмы и цилиндра. Объемы наклонной призмы, пирамиды и конуса. Объемы шара и площадь сферы. Объемы шарового сегмента, шарового слоя и шарового сектора.
О с н о в н а я ц е л ь – продолжить систематическое изучение многогранников и тел вращения в ходе решения задач на вычисление объемов.
В курсе стереометрии понятие объема вводится по аналогии с понятием площади плоской фигуры и формулируются основные свойства объемов.
Существование и единственность объема тела в школьном курсе математики приходится принимать без доказательства, так как вопрос об объемах принадлежит, по существу, к трудным разделам высшей математики. Поэтому нужные результаты устанавливаются, руководствуясь больше наглядными соображениями.
Учебный материал главы в основном должен усваиваться в процессе решения задач.
Обобщающее повторение. Решение задач
Требования к уровню подготовки обучающихся в 11 классе
В результате изучения математики 11 класса ученик должен знать:
значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки;
идеи расширения числовых множеств как способа построения нового математического аппарата для решения практических задач математики;
значение идей, методов и результатов алгебры и математического анализа для построения моделей реальных процессов и ситуаций;
возможности геометрии для описания свойств реальных предметов и их взаимного расположения;
универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
различие требований, предъявляемых к доказательствам в математике, естественных, социально-экономических и гуманитарных науках, на практике;
роль аксиоматики в математике; возможность построения математических теорий на аксиоматической основе; значение аксиоматики для других областей знания и для практики;
вероятностный характер различных процессов окружающего мира;
Числовые и буквенные выражения
уметь
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
применять понятия, связанные с делимостью целых чисел, при решении математических задач;
находить корни многочленов с одной переменной, раскладывать многочлен на множители;
проводить преобразования числовых и буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства;
Функции и графики
уметь
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функций, выполнять преобразования графиков;
описывать по графику и по формуле поведение и свойства функций;
решать уравнения, простейшие системы уравнений, неравенства, используя свойства функций и их графические представления;
использовать приобретенные знания и умения в практической деятельности и повседневной жизнидля:
описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков реальных процессов;
Начала математического анализа
уметь
решать рациональные, показательные и логарифмические уравнения и неравенства, иррациональные и тригонометрические уравнения, их системы;
доказывать неравенства;
решать тестовые задачи с помощью составления уравнений и неравенств, интерпретируя результат с учетом ограничений условий задачи;
изображать на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем; находить приближенные решения уравнений и их систем, используя графический метод;
решать уравнения, неравенства и системы с применением графических представлений, свойств функций;
использовать приобретенные знания и умения в практической деятельности и повседневной жизнидля:
Элементы комбинаторики, статистики и теорий вероятностей
уметь
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул, треугольника Паскаля; вычислять коэффициенты бинома Ньютона по формуле и с использованием треугольника Паскаля;
вычислять вероятности событий на основе подсчета числа исходов (простейшие случаи);
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
анализа реальных числовых данных, представленных в виде диаграмм, графиков; анализа информации статистического характера.
Геометрия
уметь
соотносить плоские геометрические фигуры и трехмерные объекты с их описанием. Чертежами, изображениями; различать и анализировать взаимное расположение фигур;
изображать геометрические фигуры и тела, выполнять чертеж по условию задачи;
решать геометрические задачи, опираясь на изученные свойства планиметрических и стереометрических фигур и отношений между ними. Применяя алгебраический и тригонометрический аппарат;
проводить доказательные рассуждения при решении задач. Доказывать основные теоремы курса;
вычислять линейные элементы и углы в пространственных конфигурациях, объемы и площади поверхностей пространственных тел и их простейших комбинаций;
применять координатно-векторный метод для вычисления отношений, расстояний и углов;
строить сечения многогранников и изображать сечения тел вращения.
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;
вычисление длин, площадей и объемов реальных объектов при решении практических задач, используя при необходимости справочники и вычислительные устройства.
Используемые педагогические технологии: здоровьесберегающая, ИКТ технологии, технология проектной деятельности, дифференцированного обучения.
Календарно-тематический план
| № урока | Название темы | Кол-во часов | Дата |
| 1-3 | Повторение | 3 |
|
|
| Гл. 1. Функции. Производные. Интегралы |
|
|
|
| Функции и их графики | 8 |
|
| 4 | Элементарные функции. | 1 |
|
| 5 | Область определения и область изменения функции. Ограниченность функций. | 1 |
|
| 6-7 | Четность, нечетность, периодичность. | 2 |
|
| 8-9 | Промежутки возрастания, убывания, знакопостоянства и нули функции. | 2 |
|
| 10-11 | Исследование функций и построение их графиков элементарными методами. | 2 |
|
|
| Предел функции и непрерывность | 5 |
|
| 12 | Понятие предела функции | 1 |
|
| 13 | Односторонние пределы. | 1 |
|
| 14 | Свойства пределов функций. | 1 |
|
| 15 | Понятие непрерывности функций | 1 |
|
| 16 | Непрерывность элементарных функций. | 1 |
|
|
| Обратные функции | 6 |
|
| 17 | Взаимно обратные функции | 1 |
|
| 18 | Обратные тригонометрические функции. | 1 |
|
| 19-20 | Примеры использования обратных тригонометрических функций. | 2 |
|
| 21 | Контрольная работа № 1 | 1 |
|
|
| Метод координат в пространстве | 18 |
|
| 22-23 | Прямоугольная система координат Координаты точки и координаты вектора | 2 |
|
| 24-26 | Простейшие задачи в координатах | 3 |
|
| 27-29 | Скалярное произведение векторов | 3 |
|
| 30-31 | Решение задач | 2 |
|
| 32-34 | Движения | 3 |
|
| 35-37 | Решение задач. Тестирование | 3 |
|
| 38 | Повторительно-обобщающий урок | 1 |
|
| 39 | Контрольная работа № 2 | 1 |
|
|
| Производная |
|
|
| 40-41 | Понятие производной | 2 |
|
| 42-43 | Производная суммы и разности | 2 |
|
| 44 | Непрерывность функции, имеющей производную | 1 |
|
| 45-46 | Производная произведения, частного | 2 |
|
| 47 | Производная элементарных функций | 1 |
|
| 48-49 | Производная сложной функции | 2 |
|
| 50 | Контрольная работа №3 | 1 |
|
| 51-54 | Диагностическая работа | 4 |
|
|
| Цилиндр, конус, шар | 20 |
|
| 55-56 | Цилиндр | 2 |
|
| 57-58 | Решение задач | 2 |
|
| 59-62 | Конус. Усеченный конус | 4 |
|
| 63-65 | Решение задач по теме «Конус» | 3 |
|
| 66-68 | Сфера и шар | 3 |
|
| 69-70 | Решение тестовых задач на тела вращения. | 2 |
|
| 71 | Контрольная работа № 3 | 1 |
|
|
| Применение производной | 16 |
|
| 72-73 | Максимум и минимум функции | 2 |
|
| 74-76 | Уравнение касательной | 3 |
|
| 77 | Приближенные вычисления. | 1 |
|
| 78-79 | Возрастание и убывание функции | 2 |
|
| 80 | Производные высших порядков | 1 |
|
| 81-82 | Экстремум функции с единственной критической точкой | 2 |
|
| 83-84 | Задачи на максимум и минимум | 2 |
|
| 85-86 | Построение графиков функций с применением производной. | 2 |
|
| 87 | Контрольная работа № 5 | 1 |
|
|
| Объемы тел | 19 |
|
| 88 | Объем прямоугольного параллелепипеда | 1 |
|
| 89 | Объем прямой призмы и цилиндра | 1 |
|
| 90-92 | Решение задач. Тестирование | 3 |
|
| 93-95 | Объем наклонной призмы, пирамиды, конуса | 3 |
|
| 96-98 | Решение задач. Тестирование | 3 |
|
| 99-100 | Объем шара и площадь сферы | 2 |
|
| 101-104 | Решение задач. тестирование | 4 |
|
| 105 | Повторительно-обобщающий урок | 1 |
|
| 106 | Контрольная работа № 6 | 1 |
|
|
| Первообразная и интеграл | 13 |
|
| 107-109 | Понятие первообразной | 3 |
|
| 110 | Площадь криволинейной трапеции | 1 |
|
| 111-112 | Определенный интеграл | 2 |
|
| 113 | Приближенное вычисление определенного интеграла | 1 |
|
| 114-116 | Формула Ньютона-Лейбница | 3 |
|
| 117 | Свойства определенных интегралов | 1 |
|
| 118 | Применение определенных интегралов в геометрических и физических задачах
|
1 |
|
| 119 | Контрольная работа № 7 | 1 |
|
|
| Обобщающее повторение | 11 |
|
| 120-126 | Решение задач. Тестирование | 7 |
|
| 127-131 | Решение геометрических задач ЕГЭ | 5 |
|
|
| Равносильность уравнений и неравенств | 4 |
|
| 132-133 | Равносильные преобразования уравнений | 2 |
|
| 134-135 | Равносильные преобразования неравенств | 2 |
|
|
| Уравнения-следствия | 8 |
|
| 136 | Понятие уравнения-следствия. | 1 |
|
| 137 | Возведение уравнения в четную степень. | 1 |
|
| 138-139 | Потенцирование логарифмических уравнений | 2 |
|
| 140-141 | Другие преобразования, приводящие к уравнению-следствию | 2 |
|
| 142-143 | Применение нескольких преобразований, приводящих к уравнению-следствию | 2 |
|
|
| Равносильность уравнений и неравенств системам | 13 |
|
| 144 | Основные понятия. | 1 |
|
| 145-147 | Решение уравнений с помощью систем | 3 |
|
| 148-150 | Уравнения вида f(α(x))=f(β(x)) | 3 |
|
| 151-153 | Решение неравенств с помощью систем | 3 |
|
| 154-156 | Неравенства вида f(α(x))f(β(x)) | 3 |
|
|
| Равносильность уравнений на множествах | 10 |
|
| 157-159 | Возведение уравнения в четную степень | 3 |
|
| 160-161 | Умножение уравнения на функцию | 2 |
|
| 162-163 | Другие преобразования уравнений | 2 |
|
| 164-165 | Применение нескольких преобразований | 2 |
|
| 166 | Контрольная работа № 8 | 1 |
|
|
| Равносильность неравенств на множествах | 7 |
|
| 167-168 | Возведение неравенства в четную степень | 2 |
|
| 169-170 | Умножение неравенств на функцию | 2 |
|
| 171 | Другие преобразования неравенств | 1 |
|
| 172 | Применение нескольких преобразований | 1 |
|
| 173 | Нестрогие неравенства | 1 |
|
|
| Метод промежутков для уравнений и неравенств | 4 |
|
| 174 | Уравнения с модулями | 1 |
|
| 175 | Неравенства с модулями | 1 |
|
| 176 | Метод интервалов для непрерывных функций | 1 |
|
| 177 | Контрольная работа № 9 | 1 |
|
|
| Использование свойств функций при решении уравнений и неравенств | 5 |
|
| 178 | Использование областей существования функций | 1 |
|
| 179 | Использование неотрицательности функций | 1 |
|
| 180 | Использование ограниченности функций | 1 |
|
| 181 | Использование монотонности и экстремумов функций | 1 |
|
| 182 | Использование свойств синуса и косинуса | 1 |
|
|
| Системы уравнений с несколькими неизвестными | 7 |
|
| 183 | Равносильность систем | 1 |
|
| 184 | Система-следствие | 1 |
|
| 185-187 | Метод замены неизвестных | 3 |
|
| 188-189 | Рассуждения с числовыми значениями при решении систем уравнений | 2 |
|
|
| Повторение | 21 |
|
| 190-193 | Решение тестовых заданий с выбором ответа. | 4 |
|
| 194-197 | Решение тестовых заданий с числовым ответом | 4 |
|
| 198-201 | Решение тестовых заданий с полным ответом | 4 |
|
| 202-206 | Решение типовых тестовых заданий ЕГЭ | 5 |
|
| 207-210 | Решение типовых тестовых заданий ЕГЭ | 4 |
|
Учебно –методическое и материально техническое обеспечение
Алгебра и начала математического анализа. Дидактические материалы. 11 класс/ М. К. Потапов, А.В. Шевкин. М.: Просвещение, 2010.
Алгебра и начала математического анализа Тематические тесты. 11 класс/П.В. Чулков, Т.С. Струков. М.: Просвещение, 2010.
Л.С. Атанасян, В.Ф. Бутузов Геометрия: учебник для 10 – 11 кл. общеобразовательных учреждений / М.: Просвещение, 2009.
Б.Г. Зив Дидактические материалы по геометрии для 11 кл. / М.: Просвещение, 2009.
С.М. Саакян, В.Ф. Бутузов Изучение геометрии в 10 – 11 кл.: методические рекомендации к учебнику. Книга для учителя / М.: Просвещение, 2009.
А.П. Ершова Алгебра и начала математического анализа. 11 класс: учебник/С.М.Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин, В.В. Голобородько Самостоятельные и контрольные работы по геометрии для 11 кл. (разноуровневые дидактические материалы) / М.: Илекса, 2003.
Б.Г. Зив и др. Задачи по геометрии для 7 – 11 классов / М.: Просвещение, 2009.
Е.М. Рабинович Задачи и упражнения на готовых чертежах. Геометрия / М.: Илекса, 2001.
14. http://karmanform.ucoz.ru/load/3-6-2 презентации по математике
15. http //karmanform.ucoz.ru/index/0-10 материалы по математике 10 класс







 по графику функции
по графику функции  .
. относительно прямой
относительно прямой  . По графику функции
. По графику функции  и
и 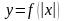 . Затем строятся графики функций, являющихся суперпозицией, суммой, произведением. функций.
. Затем строятся графики функций, являющихся суперпозицией, суммой, произведением. функций.  ,
,  , затем в точке. Рассматриваются односторонние пределы и свойства пределов функций. Вводится функций. Вводится понятие непрерывности функции в точке и на интервале. Выясняются промежутки непрерывности элементарных функций.
, затем в точке. Рассматриваются односторонние пределы и свойства пределов функций. Вводится функций. Вводится понятие непрерывности функции в точке и на интервале. Выясняются промежутки непрерывности элементарных функций. и непрерывности функции на отрезке. Приводится также определение предела функции в точке «на языке
и непрерывности функции на отрезке. Приводится также определение предела функции в точке «на языке » и «на языке последовательностей». Вводится понятие разрывной функции и рассматриваются примеры разрывных функций.
» и «на языке последовательностей». Вводится понятие разрывной функции и рассматриваются примеры разрывных функций. Решение неравенств с помощью систем. Неравенства вида
Решение неравенств с помощью систем. Неравенства вида 
 , непрерывных на некоторых интервалах, рассматривается способ решения неравенств
, непрерывных на некоторых интервалах, рассматривается способ решения неравенств  и
и  , называемый методом интервалов.
, называемый методом интервалов.









