МИНИСТЕРСТВО ПРОСВЕЩЕНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Муниципальное общеобразовательное автономное учреждение
"Лицей № 5 имени Героя РФ А.Ж. Зеленко"
| РАССМОТРЕНО Руководитель МО ________________________ Левина Ю.М. ____ от «___»____ 2024 г.
| СОГЛАСОВАНО Зам по УВР ________________________ Растемешина С.М. ____ от «___»____ 2024 г.
| УТВЕРЖДЕНО Директор ________________________ Иванова Е.В. ____ от «___»____ 2024 г.
|
РАБОЧАЯ ПРОГРАММА
(ID 4631055)
учебного предмета «Наглядная геометрия»
для обучающихся 5-6 классов
на 2024-2026 учебные годы
Составитель: Мокшина Екатерина Александровна,
учитель математики
первой квалификационной категории
г. Оренбург, 2024
Пояснительная записка
Результаты ГИА и ЕГЭ по математике показывают, что основная проблема геометрической подготовки учащихся связана с недостаточно развитыми геометрическими представлениями, неумением представлять и изображать геометрические фигуры, проводить дополнительные построения. Задачи, в которых требуется понимание геометрической конструкции, решаются гораздо хуже, чем те, в которых требуется просто найти ту или иную геометрическую величину, подставляя данные в соответствующую формулу.
Выучивание формул не является основной целью обучения геометрии. В некотором смысле геометрические представления учащихся важнее знания конкретных формул. Формулы забываются, а геометрические представления остаются. Формулы можно посмотреть в справочной литературе, а геометрические представления нет. Начинать развивать геометрические представления школьников нужно как можно раньше. К сожалению, в действующих учебниках по математике для 5-6 классов больше внимания уделяется вопросам нахождения геометрических величин (длина, угол, площадь, объём) и гораздо меньше – развитию геометрических представлений учащихся. Изучение наглядной геометрии в 5-6 классе, позволит развить геометрические представления учащихся, лучше подготовить их к изучению систематического курса геометрии 7-11 классов, повысить качество обучения геометрии.
Содержание линии предметного курса «Наглядная геометрия» способствует формированию у учащихся первичных представлений о геометрических абстракциях реального мира, закладывает основы формирования правильной геометрической речи, развивает образное мышление и пространственные представления.
В программе предметного курса «Наглядная геометрия» учитываются основные идеи и положения программы развития и формирования универсальных учебных действий.
Рабочая программа по предметному курсу составлена на основе учебно-методического комплекта:
Смирнов В. А., Смирнова И. В., Ященко И. В. Наглядная геометрия. - М.: МЦНМО. 2013. - 272 с.
Смирнов В. А., Смирнова И. В., Ященко И. В. Наглядная геометрия. Рабочая тетрадь №1.- М.: МЦНМО. 2012. - 88 с.
Смирнов В. А., Смирнова И. В., Ященко И. В. Наглядная геометрия. Рабочая тетрадь №2.- М.: МЦНМО. 2012. - 88 с.
Смирнов В. А., Смирнова И. В., Ященко И. В. Наглядная геометрия. Рабочая тетрадь №3.- М.: МЦНМО. 2012. - 88 с.
Смирнов В. А., Смирнова И. В., Ященко И. В. Наглядная геометрия. Рабочая тетрадь №4.- М.: МЦНМО. 2012. - 88 с.
Данный курс предназначен для обучающихся 5-6 классов и имеет практико-ориентированную направленность. Курс включает в себя задания, как углубляющего, так и развивающего характера. На изучение курса отводится 136 часов: в 5 классе - 68 часов (2 часа в неделю, 34 учебные недели), в 6 классе - 68 часов (2 часа в неделю, 34 учебные недели).
Цели курса “Наглядная геометрия”: через систему задач организовать интеллектуально-практическую и исследовательскую деятельность обучающихся, направленную на:
- развитие пространственных представлений, образного мышления, изобразительно графических умений, приемов конструктивной деятельности, умений преодолевать трудности при решении математических задач, геометрической интуиции, познавательного интереса обучающихся, развитие глазомера, памяти, обучение правильной геометрической речи;
- формирование логического и абстрактного мышления, формирование качеств личности (ответственность, добросовестность, дисциплинированность, аккуратность, усидчивость).
Задачи курса “Наглядная геометрия”:
- Вооружить обучающихся определенным объемом геометрических знаний и умений, необходимых им для нормального восприятия окружающей деятельности. Познакомить учеников с геометрическими фигурами и понятиями на уровне представлений, изучение свойств на уровне практических исследований, применение полученных знаний при решении различных задач. Основными приемами решения задач являются: наблюдение, конструирование, эксперимент.
- Развитие логического мышления обучающихся через решение соответствующих задач, как правило, “в картинках”.
- На занятиях наглядной геометрии предусмотрено решение интересных головоломок, занимательных задач, бумажных геометрических игр и т.п. Этот курс поможет развить у ребят смекалку и находчивость при решении задач.
- Приобретение новых знаний обучающимися осуществляется в основном в ходе их самостоятельной деятельности. Среди задачного и теоретического материала акцент делается на упражнения, развивающие “геометрическую зоркость”, интуицию и воображение обучающихся. Уровень сложности задач таков, чтобы их решения были доступны большинству учеников.
Содержание обучения
Основные понятия геометрии
Точки, прямые, плоскости. Лучи и отрезки. Взаимное расположение точек и прямых на плоскости. Параллельные и перпендикулярные прямые.
Отрезки и углы
Сравнение отрезков. Равенство отрезков. Измерение длин отрезков. Единицы измерения длины.
Полуплоскость и угол. Виды углов: острые, прямые, тупые углы, развёрнутый угол. Смежные и вертикальные углы. Сравнение углов. Равенство углов. Биссектриса угла. Градусная величина угла. Измерение величин углов.
Ломаные и многоугольники
Ломаная. Простые и замкнутые ломаные. Длина ломаной. Многоугольник. Диагонали многоугольника. Выпуклые и невыпуклые многоугольники. Правильные многоугольники. Звёздчатые многоугольники. Периметр многоугольника.
Треугольники и четырёхугольники
Остроугольные, прямоугольные, тупоугольные, равнобедренные, равносторонние треугольники. Гипотенуза и катеты прямоугольного треугольника. Высота, медиана и биссектриса треугольника. Построение треугольников по двум сторонам и углу между ними. Построение треугольников по стороне и двум прилежащим к ней углам, по трем сторонам.
Четырёхугольник. Выпуклые и невыпуклые четырёхугольники. Прямоугольник, квадрат, параллелограмм, ромб, трапеция. Равнобедренная и прямоугольная трапеции.
Многогранники
Понятие многогранника. Вершины, рёбра и грани многогранника. Выпуклые и невыпуклые многогранники. Куб, параллелепипед, призма, пирамида. Правильные, полуправильные и звёздчатые многогранники. Развёртки. Моделирование многогранников. Конструкции из кубиков.
Окружность. Геометрические места точек
Окружность и круг. Центр и радиус окружности. Хорда и диаметр окружности. Взаимное расположение двух окружностей. Длина окружности.
Геометрическое место точек. Примеры.
Графы. Кривые
Графы. Вершины и рёбра графов. Примеры графов. Уникурсальные графы. Задача Эйлера о кёнигсбергских мостах. Задачи о раскрашивании карт. Задачи со спичками.
Кривые, как траектории движения точек: циклоида, кардиоида, астроида.
Симметрия
Центральная симметрия. Центрально - симметричные фигуры. Примеры.
Осевая симметрия. Примеры. Поворот. Симметрия n-го порядка. Примеры. Изображение симметричных фигур. Паркеты на плоскости. Правильные паркеты. Параллельный перенос. Линейные орнаменты (бордюры). Оригами.
Площадь и объём
Площадь и её свойства. Единицы измерения площади. Равновеликие фигуры. Площадь прямоугольника, параллелограмма, треугольника, многоугольника. Задачи на разрезание. Площадь поверхности многогранника. Объём и его свойства. Единицы измерения объёма. Объём прямоугольного параллелепипеда и прямой призмы. Геометрия клетчатой бумаги.
Координаты
Прямоугольная система координат на плоскости. Начало координат. Координатные прямые: оси абсцисс и ординат. Координаты точки. Метод координат. Построение фигур и рисунков в системе координат. Игры в координатах. Координаты точки на прямой, на плоскости и в пространстве.
Планируемые результаты
Личностные результаты освоения программы учебного курса «Наглядная геометрия» характеризуются:
1) патриотическое воспитание:
проявлением интереса к прошлому и настоящему российской математики, ценностным отношением к достижениям российских математиков и российской математической школы, к использованию этих достижений в других науках и прикладных сферах;
2) гражданское и духовно-нравственное воспитание:
готовностью к выполнению обязанностей гражданина и реализации его прав, представлением о математических основах функционирования различных структур, явлений, процедур гражданского общества (например, выборы, опросы), готовностью к обсуждению этических проблем, связанных с практическим применением достижений науки, осознанием важности морально-этических принципов в деятельности учёного;
3) трудовое воспитание:
установкой на активное участие в решении практических задач математической направленности, осознанием важности математического образования на протяжении всей жизни для успешной профессиональной деятельности и развитием необходимых умений, осознанным выбором и построением индивидуальной траектории образования и жизненных планов с учётом личных интересов и общественных потребностей;
4) эстетическое воспитание:
способностью к эмоциональному и эстетическому восприятию математических объектов, задач, решений, рассуждений, умению видеть математические закономерности в искусстве;
5) ценности научного познания:
ориентацией в деятельности на современную систему научных представлений об основных закономерностях развития человека, природы и общества, пониманием математической науки как сферы человеческой деятельности, этапов её развития и значимости для развития цивилизации, овладением языком математики и математической культурой как средством познания мира, овладением простейшими навыками исследовательской деятельности;
6) физическое воспитание, формирование культуры здоровья и эмоционального благополучия:
готовностью применять математические знания в интересах своего здоровья, ведения здорового образа жизни (здоровое питание, сбалансированный режим занятий и отдыха, регулярная физическая активность), сформированностью навыка рефлексии, признанием своего права на ошибку и такого же права другого человека;
7) экологическое воспитание:
ориентацией на применение математических знаний для решения задач в области сохранности окружающей среды, планирования поступков и оценки их возможных последствий для окружающей среды, осознанием глобального характера экологических проблем и путей их решения;
8) адаптация к изменяющимся условиям социальной и природной среды:
готовностью к действиям в условиях неопределённости, повышению уровня своей компетентности через практическую деятельность, в том числе умение учиться у других людей, приобретать в совместной деятельности новые знания, навыки и компетенции из опыта других;
необходимостью в формировании новых знаний, в том числе формулировать идеи, понятия, гипотезы об объектах и явлениях, в том числе ранее неизвестных, осознавать дефициты собственных знаний и компетентностей, планировать своё развитие;
способностью осознавать стрессовую ситуацию, воспринимать стрессовую ситуацию как вызов, требующий контрмер, корректировать принимаемые решения и действия, формулировать и оценивать риски и последствия, формировать опыт.
Метапредметные результаты
Познавательные универсальные учебные действия
Базовые логические действия:
выявлять и характеризовать существенные признаки математических объектов, понятий, отношений между понятиями, формулировать определения понятий, устанавливать существенный признак классификации, основания для обобщения и сравнения, критерии проводимого анализа;
воспринимать, формулировать и преобразовывать суждения: утвердительные и отрицательные, единичные, частные и общие, условные;
выявлять математические закономерности, взаимосвязи и противоречия в фактах, данных, наблюдениях и утверждениях, предлагать критерии для выявления закономерностей и противоречий;
делать выводы с использованием законов логики, дедуктивных и индуктивных умозаключений, умозаключений по аналогии;
разбирать доказательства математических утверждений (прямые и от противного), проводить самостоятельно несложные доказательства математических фактов, выстраивать аргументацию, приводить примеры и контрпримеры, обосновывать собственные рассуждения;
выбирать способ решения учебной задачи (сравнивать несколько вариантов решения, выбирать наиболее подходящий с учётом самостоятельно выделенных критериев).
Базовые исследовательские действия:
использовать вопросы как исследовательский инструмент познания, формулировать вопросы, фиксирующие противоречие, проблему, самостоятельно устанавливать искомое и данное, формировать гипотезу, аргументировать свою позицию, мнение;
проводить по самостоятельно составленному плану несложный эксперимент, небольшое исследование по установлению особенностей математического объекта, зависимостей объектов между собой;
самостоятельно формулировать обобщения и выводы по результатам проведённого наблюдения, исследования, оценивать достоверность полученных результатов, выводов и обобщений;
прогнозировать возможное развитие процесса, а также выдвигать предположения о его развитии в новых условиях.
Работа с информацией:
выявлять недостаточность и избыточность информации, данных, необходимых для решения задачи;
выбирать, анализировать, систематизировать и интерпретировать информацию различных видов и форм представления;
выбирать форму представления информации и иллюстрировать решаемые задачи схемами, диаграммами, иной графикой и их комбинациями;
оценивать надёжность информации по критериям, предложенным учителем или сформулированным самостоятельно.
Коммуникативные универсальные учебные действия:
воспринимать и формулировать суждения в соответствии с условиями и целями общения, ясно, точно, грамотно выражать свою точку зрения в устных и письменных текстах, давать пояснения по ходу решения задачи, комментировать полученный результат;
в ходе обсуждения задавать вопросы по существу обсуждаемой темы, проблемы, решаемой задачи, высказывать идеи, нацеленные на поиск решения, сопоставлять свои суждения с суждениями других участников диалога, обнаруживать различие и сходство позиций, в корректной форме формулировать разногласия, свои возражения;
представлять результаты решения задачи, эксперимента, исследования, проекта, самостоятельно выбирать формат выступления с учётом задач презентации и особенностей аудитории;
понимать и использовать преимущества командной и индивидуальной работы при решении учебных математических задач;
принимать цель совместной деятельности, планировать организацию совместной работы, распределять виды работ, договариваться, обсуждать процесс и результат работы, обобщать мнения нескольких людей;
участвовать в групповых формах работы (обсуждения, обмен мнениями, мозговые штурмы и другие), выполнять свою часть работы и координировать свои действия с другими членами команды, оценивать качество своего вклада в общий продукт по критериям, сформулированным участниками взаимодействия.
Регулятивные универсальные учебные действия
Самоорганизация:
самостоятельно составлять план, алгоритм решения задачи (или его часть), выбирать способ решения с учётом имеющихся ресурсов и собственных возможностей, аргументировать и корректировать варианты решений с учётом новой информации.
Самоконтроль, эмоциональный интеллект:
владеть способами самопроверки, самоконтроля процесса и результата решения математической задачи;
предвидеть трудности, которые могут возникнуть при решении задачи, вносить коррективы в деятельность на основе новых обстоятельств, найденных ошибок, выявленных трудностей;
оценивать соответствие результата деятельности поставленной цели и условиям, объяснять причины достижения или недостижения цели, находить ошибку, давать оценку приобретённому опыту.
Предметные результаты
К концу обучения в 5 классе обучающийся получит следующие предметные результаты по отдельным темам рабочей программы учебного курса «Наглядная геометрия»:
Основные понятия геометрии:
понимать, идеализацией каких реальных объектов являются точки, прямые и плоскости;
изображать, обозначать и называть точки, прямые, лучи, отрезки;
устанавливать взаимное расположение точек и прямых на плоскости;
решать задачи комбинаторного характера на взаимное расположение точек и прямых на плоскости.
Отрезки и углы:
сравнивать отрезки и устанавливать их равенство;
измерять длины отрезков с помощью линейки;
откладывать отрезки заданной длины;
изображать, обозначать и называть углы;
устанавливать виды углов;
сравнивать углы и устанавливать их равенство;
проводить биссектрису угла;
измерять градусные величины углов с помощью транспортира;
изображать углы заданных градусных величин;
решать задачи на нахождение длин отрезков и величин углов.
Ломаные и многоугольники:
изображать, обозначать и называть ломаные и многоугольники;
устанавливать вид многоугольников;
проводить дополнительные построения;
находить длину ломаной и периметр многоугольника.
Треугольники и четырёхугольники:
изображать, обозначать и называть треугольники и четырёхугольники;
устанавливать вид треугольников и четырёхугольников;
проводить дополнительные построения;
решать задачи на нахождение сторон и углов треугольников и четырёхугольников.
Многогранники:
изображать многогранники;
устанавливать выпуклость и невыпуклость многогранников;
находить число вершин, рёбер и граней многогранников;
изготавливать развёртки многогранников;
моделировать многогранники.
К концу обучения в 6 классе обучающийся получит следующие предметные результаты по отдельным темам рабочей программы учебного курса «Наглядная геометрия»:
Окружность. Геометрические места точек:
изображать окружности и круги;
отмечать центр окружности, проводить радиус, диаметр и хорды окружности;
устанавливать взаимное расположение окружностей;
находить приближённое значение длины окружности;
решать задачи на нахождение и изображение геометрических мест точек.
Графы. Кривые:
приводить примеры графов и изображать графы;
устанавливать уникурсальность графов;
решать задачи на раскрашивание карт;
изображать кривые, как траектории движения точек.
Симметрия:
изображать фигуру, центрально-симметричную данной;
устанавливать центральную симметричность фигур и находить их центр симметрии;
изображать фигуру, симметричную данной относительно заданной оси;
находить и изображать оси симметрии заданных фигур;
изображать фигуру, полученную поворотом данной фигуры на данный угол вокруг данной точки;
выяснять порядок симметрии данной фигуры и изображать центр симметрии;
изображать паркеты на плоскости, выяснять возможность построения паркетов из заданных многоугольников.
Площадь и объём:
находить площади фигур, используя формулы и свойства площади;
устанавливать равновеликость фигур;
решать задачи на разрезание;
находить площади поверхностей многогранников;
находить объёмы многогранников, используя формулы и свойства объёмов.
Координаты:
изображать прямоугольную систему координат на плоскости;
находить координаты точек и изображать точки с заданными координатами;
изображать отрезки, ломанные, многоугольники на координатной плоскости, заданные координатами центра и радиусом;
решать задачи на нахождение длин, углов, площадей фигур на координатной плоскости.
Тематическое планирование
5 класс
| № п/п
| Наименование разделов и тем программы
| Количество часов |
| 1 | Основные понятия геометрии | 9 |
| 2 | Отрезки и углы | 12 |
| 3 | Ломаные и многоугольники | 6 |
| 4 | Треугольники и четырёхугольники | 19 |
| 5 | Многогранники | 16 |
| 6 | Повторение и обобщение | 6 |
6 класс
| № п/п
| Наименование разделов и тем программы
| Количество часов |
| 1 | Окружность. Геометрические места точек | 4 |
| 2 | Графы. Кривые | 7 |
| 3 | Симметрия | 8 |
| 4 | Площадь и объём | 9 |
| 5 | Координаты | 3 |
| 6 | Повторение и обобщение | 3 |
Поурочное планирование
5 класс
| № п/п | Тематика занятий | Дата проведения |
| План | Факт |
| Вводное занятие. Возникновение геометрии из практики. | 2.09-07.09 |
|
| Стартовая диагностика | 2.09-07.09 |
|
|
| Основные понятия геометрии |
|
|
| Точки, прямые, плоскости | 09.09-14.09 |
|
| Лучи, отрезки | 09.09-14.09 |
|
| Простейшие геометрические фигуры: точки, прямые, плоскости, лучи, отрезки | 16.09-21.09 |
|
| Взаимное расположение точек и прямых на плоскости. | 16.09-21.09 |
|
| Параллельные прямые. | 23.09-28.09 |
|
| Перпендикулярные прямые | 23.09-28.09 |
|
| Параллельные и перпендикулярные прямые | 30.09-05.10 |
|
| Параллельные и перпендикулярные прямые | 30.09-05.10 |
|
|
| Отрезки и yглы |
|
|
| Сравнение отрезков. Равенство отрезков. | 07.10-12.10 |
|
| Измерение длин отрезков. Единицы измерения длины. | 07.10-12.10 |
|
| Измерение длин отрезков. | 14.10-19.10 |
|
| Полуплоскость и угол. Виды углов: острые, прямые, тупые углы, развёрнутый угол. | 14.10-19.10 |
|
| Смежные и вертикальные углы. | 21.10-25.10 |
|
| Смежные и вертикальные углы. | 21.10-25.10 |
|
| Сравнение углов. Равенство углов. | 05.11-09.11 |
|
| Биссектриса угла. Градусная величина угла. | 05.11-09.11 |
|
| Биссектриса угла. Градусная величина угла. | 11.11-16.11 |
|
| Измерение величин углов | 11.11-16.11 |
|
| Измерение величин углов | 18.11-23.11 |
|
| Контрольная работа № 1 «Отрезки и углы» | 18.11-23.11 |
|
|
| Ломаные и многоугольники |
|
|
| Ломаная. Простые и замкнутые ломаные. | 25.11-30.11 |
|
| Длина ломаной. Многоугольник. | 25.11-30.11 |
|
| Длина ломаной. Многоугольник. | 02.12-07.12 |
|
| Диагонали многоугольника. Выпуклые и невыпуклые многоугольники. | 02.12-07.12 |
|
| Звёздчатые многоугольники. Периметр многоугольника. | 09.12-14.12 |
|
| Периметр многоугольника. | 09.12-14.12 |
|
|
| Треугольники и четырехугольники |
|
|
| Остроугольные, прямоугольные, тупоугольные треугольники. | 16.12-21.12 |
|
| Равнобедренные, равносторонние треугольники | 16.12-21.12 |
|
| Гипотенуза и катеты прямоугольного треугольника. | 23.12-28.12 |
|
| Треугольники. Высота, медиана и биссектриса треугольника. | 23.12-28.12 |
|
| Треугольники. Высота, медиана и биссектриса треугольника. | 09.01-11.01 |
|
| Треугольник. Построение треугольников по двум сторонам и углу между ними. | 09.01-11.01 |
|
| Треугольник. Построение треугольников по стороне и двум прилежащим к ней углам. | 13.01-18.01 |
|
| Треугольник. Построение треугольников по трем сторонам. | 13.01-18.01 |
|
| Четырёхугольник. Выпуклые и невыпуклые четырёхугольники. | 20.01-25.01 |
|
| Четырёхугольник. Выпуклые и невыпуклые четырёхугольники. | 20.01-25.01 |
|
| Прямоугольник, квадрат. | 27.01-01.02 |
|
| Прямоугольник, квадрат. | 27.01-01.02 |
|
| Параллелограмм. | 03.02-08.02 |
|
| Ромб. | 03.02-08.02 |
|
| Ромб, трапеция | 10.02-15.02 |
|
| Равнобедренная и прямоугольная трапеции. | 10.02-15.02 |
|
| Равнобедренная и прямоугольная трапеции. | 17.02-22.02 |
|
| Треугольники и четырехугольники. | 17.02-22.02 |
|
| Контрольная работа № 2 «Многоугольники. Треугольники и четырёхугольники» | 24.02-01.03 |
|
|
| Многогранники |
|
|
| Понятие многогранника. Вершины, рёбра и грани многогранника. | 24.02-01.03 |
|
| Выпуклые и невыпуклые многогранники. | 03.03-07.03 |
|
| Моделирование многогранников | 03.03-07.03 |
|
| Моделирование многогранников | 10.03-15.03 |
|
| Куб. Развёртка. | 10.03-15.03 |
|
| Параллелепипед. Развертка. | 17.03-22.03 |
|
| Куб, параллелепипед | 17.03-22.03 |
|
| Призма. Развёртка. | 24.03-25.03 |
|
| Пирамида. Развёртка. | 24.03-25.03 |
|
| Призма, пирамида. | 04.04-05.04 |
|
| Правильные, полуправильные многогранники | 04.04-05.04 |
|
| 3вёздчатые многогранники | 07.04-12.04 |
|
| Многогранники | 07.04-12.04 |
|
| Многогранники. Конструкции из кубиков | 14.04-19.04 |
|
| Многогранники. Конструкции из кубиков | 14.04-19.04 |
|
| Контрольная работа № 3 «Многогранники» | 21.04-26.04 |
|
| Повторение. Отрезки, углы, ломаные. | 21.04-26.04 |
|
| Повторение. Многоугольники. | 27.04-03.05 |
|
| Повторение. Треугольники и четырехугольники | 05.05-10.05. |
|
| Повторение. Многогранники. | 12.05-17.05 |
|
| Промежуточная аттестация. Контрольная работа | май |
|
6 класс
| № п/п | Тематика занятий | Дата проведения |
| План | Факт |
| Повторение. Углы, Ломаные, многоугольники |
|
|
| Повторение. Многогранники |
|
|
| Входная контрольная работа |
|
|
|
| Окружность. Геометрические места точек |
|
|
| Окружность и круг. Центр и радиус окружности. |
|
|
| Окружность и круг. Хорда и диаметр окружности. |
|
|
| Взаимное расположение двух окружностей. |
|
|
| Длина окружности. |
|
|
| Площадь круга. |
|
|
| Длина окружности. Площадь круга. |
|
|
| Длина окружности. Площадь круга. |
|
|
| Геометрическое место точек. Примеры. |
|
|
|
| Графы. Кривые |
|
|
| Графы. Вершины и рёбра графов. Примеры графов. |
|
|
| Уникурсальные графы. Задача Эйлера о кёнигсбергских мостах. |
|
|
| Задачи о раскрашивании карт. |
|
|
| Кривые, как траектории движения точек: циклоида, кардиоида, астроида. |
|
|
| Задачи со спичками. |
|
|
| Контрольная работа № 1 «Окружность. Графы» |
|
|
|
| Симметрия |
|
|
| Центральная симметрия. Центрально - симметричные фигуры. Примеры. |
|
|
| Центральная симметрия. Центрально - симметричные фигуры. Примеры. |
|
|
| Осевая симметрия. Примеры. |
|
|
| Осевая симметрия. Примеры. |
|
|
| Изображение симметричных фигур. |
|
|
| Изображение симметричных фигур. |
|
|
| Поворот. Симметрия n-го порядка. Примеры. |
|
|
| Поворот. Симметрия n-го порядка. Примеры. |
|
|
| Параллельный перенос |
|
|
| Параллельный перенос |
|
|
| Паркеты на плоскости. Правильные паркеты. |
|
|
| Паркеты на плоскости. Правильные паркеты. |
|
|
| Линейные орнаменты (бордюры). |
|
|
| Линейные орнаменты (бордюры). |
|
|
| Оригами |
|
|
| Оригами |
|
|
| Контрольная работа № 2. «Симметрия» |
|
|
|
| Площадь и объём |
|
|
| Площадь и её свойства. Единицы измерения площади. |
|
|
| Равновеликие фигуры. Площадь прямоугольника. |
|
|
| Площадь параллелограмма |
|
|
| Площадь треугольника. |
|
|
| Площадь многоугольника. |
|
|
| Площадь треугольника и многоугольника |
|
|
| Задачи на разрезание. |
|
|
| Задачи на разрезание. |
|
|
| Геометрия клетчатой бумаги |
|
|
| Геометрия клетчатой бумаги |
|
|
| Площадь поверхности многогранника. |
|
|
| Площадь поверхности многогранника. |
|
|
| Площадь поверхности многогранника. |
|
|
| Объём и его свойства. Единицы измерения объёма. |
|
|
| Объём прямоугольного параллелепипеда. |
|
|
| Объём прямой призмы. |
|
|
| Объём прямоугольного параллелепипеда и прямой призмы |
|
|
| Объём прямоугольного параллелепипеда и прямой призмы |
|
|
| Контрольная работа № 3. «Площадь и объем» |
|
|
|
| Координаты |
|
|
| Прямоугольная система координат на плоскости. Начало координат. Координатные прямые: оси абсцисс и ординат. Координаты точки. |
|
|
| Координаты точки. Метод координат. |
|
|
| Координаты точки. Метод координат. |
|
|
| Координаты точки на прямой, на плоскости и в пространстве |
|
|
| Координаты точки на прямой, на плоскости и в пространстве |
|
|
| Построение фигур и рисунков в системе координат. |
|
|
| Построение фигур и рисунков в системе координат. |
|
|
| Игры в координатах. |
|
|
| Игры в координатах. |
|
|
| Контрольная работа № 4. «Координаты» |
|
|
| Повторение. Окружность. Геометрические места точек |
|
|
| Повторение. Симметрия. Графы. Кривые. |
|
|
| Повторение. Площадь. Объем |
|
|
| Повторение. Координаты |
|
|
| Промежуточная аттестация. Контрольная работа |
|
|
Оценочные материалы
5 класс
Стартовая диагностика
Вариант 1
Переведите.
125 см = …м …дм …см 847 дм = …м …дм
7 м 3 см = …см 700 см2 = …дм2
Начертите прямоугольник со сторонами 5 см и 3 см. Найдите его площадь и периметр.
Найти сторону квадрата, если его периметр 36 см
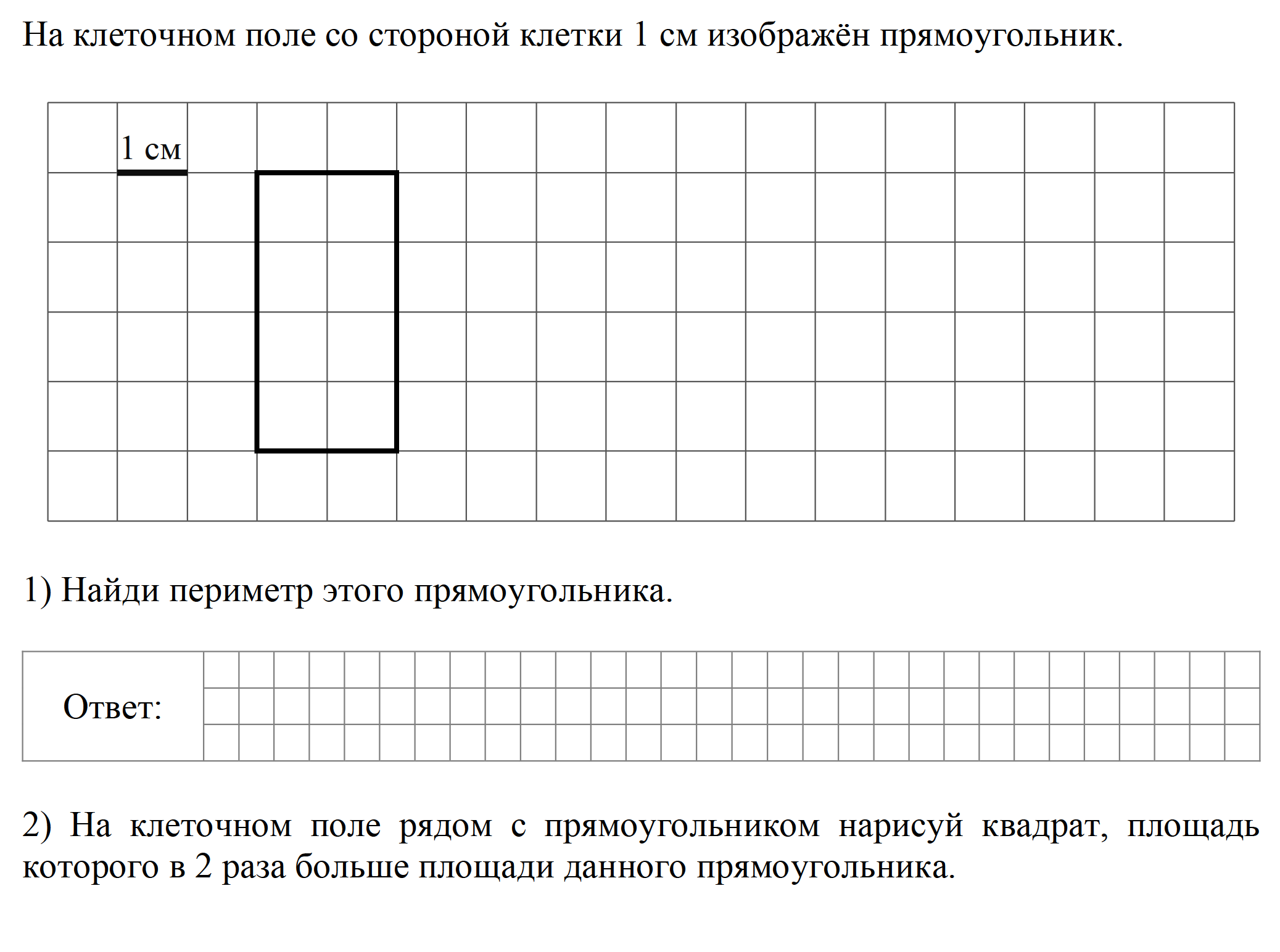

Вариант 2
Переведите.
8 м 4 см = …см 275 см = …м …дм …см
900 см2 = …дм2 631 дм = …м …дм
Начертите прямоугольник со сторонами 6 см и 2 см. Найдите площадь и периметр этого прямоугольника.
Найти сторону квадрата, если его периметр 24 см.
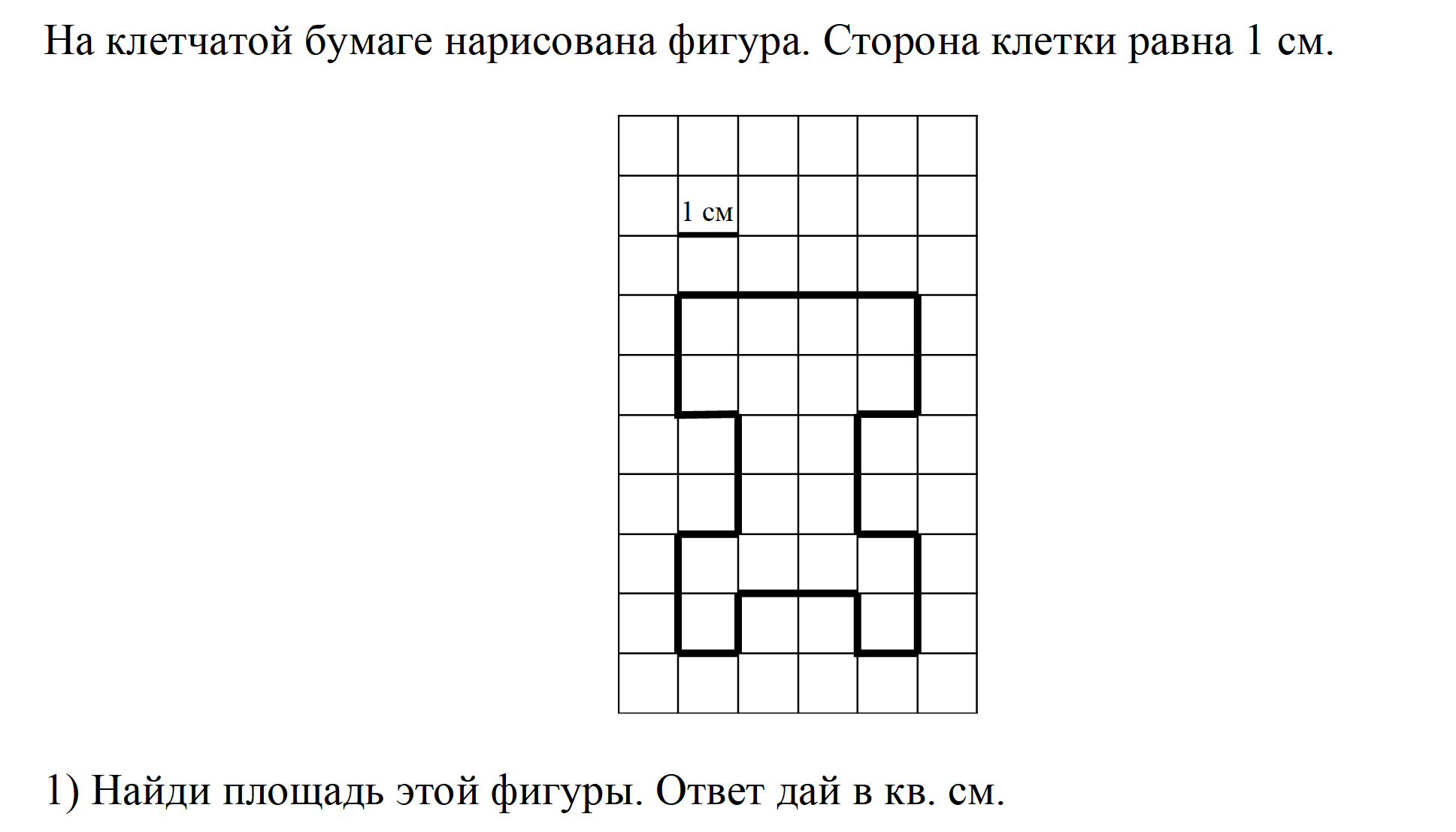
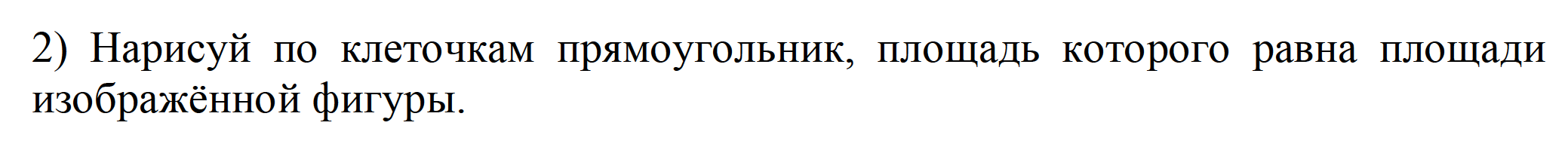
Контрольная работа «Отрезки и углы»
1 вариант
1. На прямой даны три точки А, В, С, причем АВ = 8 см, АС = 7см. Найдите длину отрезка ВС. (Задача имеет два решения)
2. Луч ОС делит развернутый угол АОВ на два смежных угла АОС и ВОС так, что угол АОС на 70° больше угла ВОС. Найдите углы АОС и ВОС.
3. При пересечении двух прямых образовались четыре угла. Определите величины этих углов, если один из них в 8 раз больше другого.
2 вариант
1. На прямой даны три точки А, В, С, причем АВ = 10см, АС = 6см. Найдите длину отрезка ВС. (Задача имеет два решения)
2. Луч ОС делит развернутый угол АОВ на два смежных угла АОС и ВОС так, что угол АОС в 2 раза больше угла ВОС. Найдите углы АОС и ВОС.
3. При пересечении двух прямых образовались четыре угла. Определите величины этих углов, если один из них на 60° больше другого.
Контрольная работа «Отрезки и углы»
1 вариант
1. На прямой даны три точки А, В, С, причем АВ = 8 см, АС = 7см. Найдите длину отрезка ВС. (Задача имеет два решения)
2. Луч ОС делит развернутый угол АОВ на два смежных угла АОС и ВОС так, что угол АОС на 70° больше угла ВОС. Найдите углы АОС и ВОС.
3. При пересечении двух прямых образовались четыре угла. Определите величины этих углов, если один из них в 8 раз больше другого.
2 вариант
1. На прямой даны три точки А, В, С, причем АВ = 10см, АС = 6см. Найдите длину отрезка ВС. (Задача имеет два решения)
2. Луч ОС делит развернутый угол АОВ на два смежных угла АОС и ВОС так, что угол АОС в 2 раза больше угла ВОС. Найдите углы АОС и ВОС.
3. При пересечении двух прямых образовались четыре угла. Определите величины этих углов, если один из них на 60° больше другого.
Контрольная работа «Многоугольники. Четырехугольники и треугольники»
Вариант 1
1. Построить прямоугольник со сторонами 4 см и 7 см и обозначьте его. Найти площадь и периметр прямоугольника.
2. Построить квадрат со стороной 5 см. Найти площадь и периметр квадрата.
3. Периметр прямоугольника 84 см, длина одной его стороны 16 см. Найти длины трех других его сторон.
4. Начертить произвольный треугольник и обозначить его. Измерить его стороны, вычислить периметр треугольника.
Пол в комнате имеет форму прямоугольника со сторонами 6 м и 4 м. Сколько квадратных паркетных досок со стороной 20см потребуется для покрытия пола?
6*.(дополнительно по желанию) Размеры оконного стекла – 100 см и 150 см. Сколько потребуется денег для установки 12 пластиковых окон, если 1 пластиковых окон стоит 6000 рублей?
Вариант 2
Построить прямоугольник со сторонами 5 см и 8 см и обозначьте его. Найти площадь и периметр прямоугольника.
2. Построить квадрат со стороной 3 см. Найти площадь и периметр квадрата.
3. Периметр прямоугольника 78 см, длина одной его стороны 12 см. Найти длины трех других его сторон.
4. Начертить произвольный треугольник и обозначить его. Измерить его стороны, вычислить периметр треугольника.
Пол в комнате имеет форму квадрата со стороной 4 м. Сколько надо паркетных дощечек прямоугольной формы со сторонами 5 см и 20 см, чтобы покрыть весь пол паркетом?
6*. (дополнительно по желанию) Размеры оконного стекла – 200 см и 250 см. Сколько потребуется денег для установки 8 пластиковых окон, если 1 пластиковых окон стоит 8000 рублей?
Контрольная работа «Многогранники»
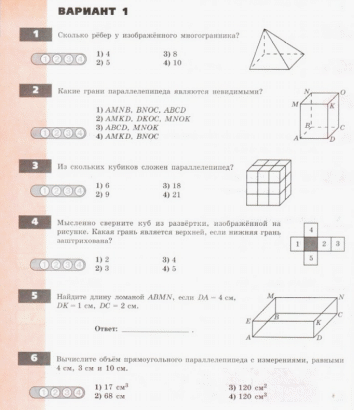

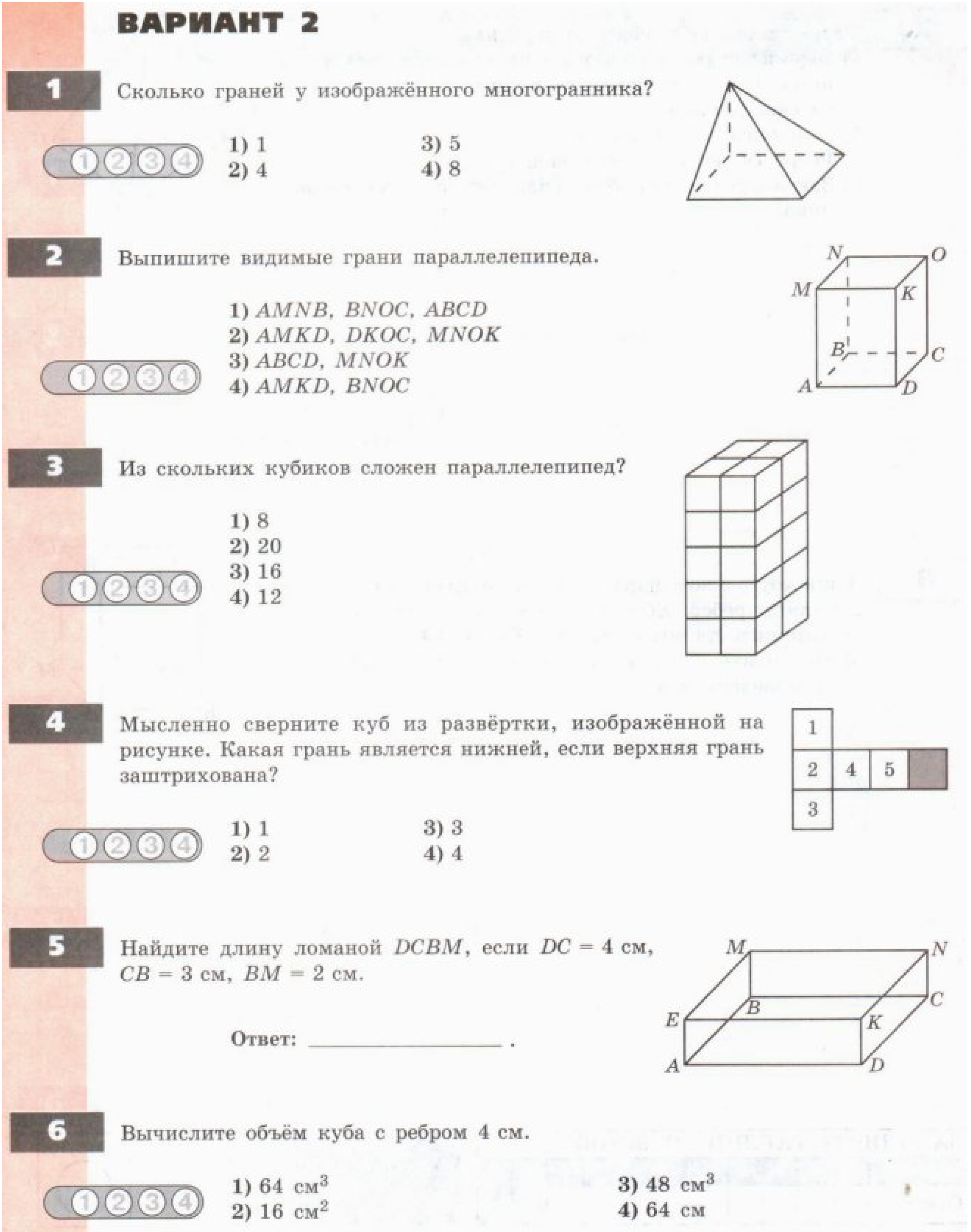

Промежуточная аттестация в 5 классе
Вариант 1.
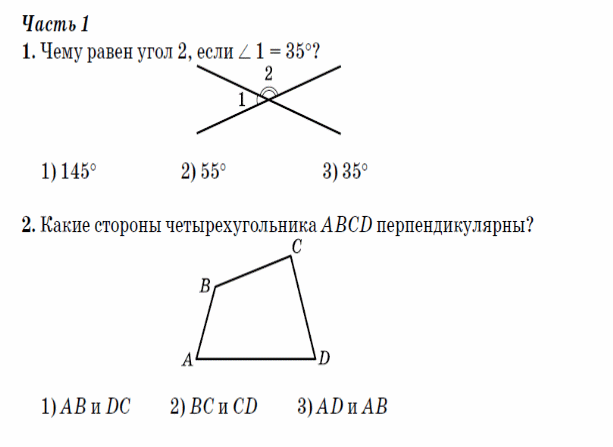

4.Исправьте в чертежах ошибки: Обведите сплошными линиями те ребра, которые должны быть видны.


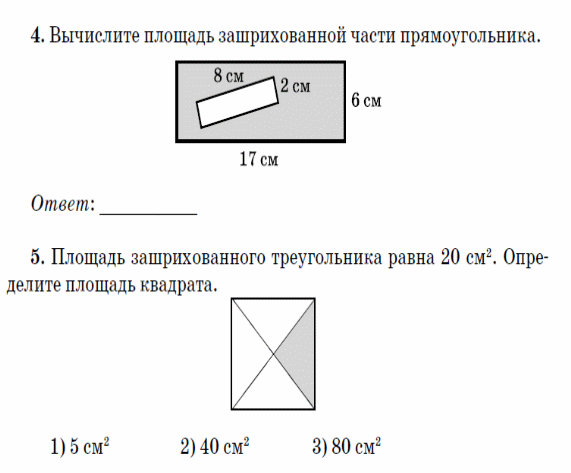
6. Постройте треугольник АРМ, у которого  А=105о,
А=105о,  В=42о. Вычислите величину третьего угла.
В=42о. Вычислите величину третьего угла.
Вариант 2.
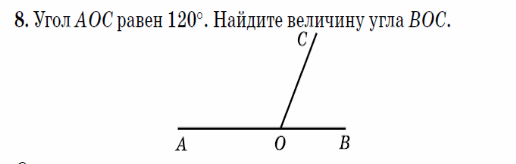
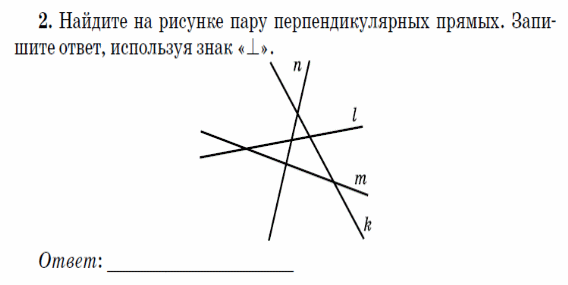
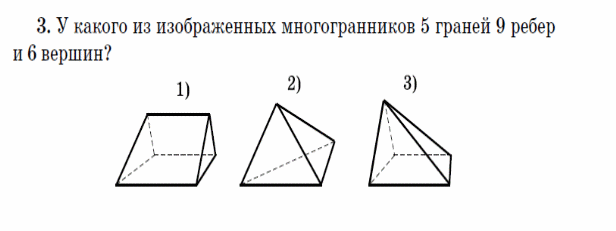
3. У какого из изображенных многогранников 5 граней 8 ребер и 5 вершин?
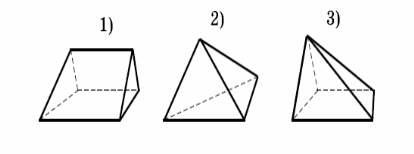
4.Исправьте в чертежах ошибки: Обведите сплошными линиями те ребра, которые должны быть видны.


Площадь квадрата равна 20 см2. Определите площадь заштрихованного треугольника.

Постройте треугольник АВМ, у которого 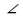 А=80о,
А=80о, 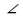 В=45о. Вычислите величину третьего угла.
В=45о. Вычислите величину третьего угла.
Оценочные материалы для 6 класса
Входная контрольная работа
Вариант 1.
Найдите площадь квадрата, сторона которого равна 9 см.
Постройте две прямые, пересекающиеся под углом 400. Найдите остальные углы.
Ширина прямоугольного участка земли 300 м, и она меньше длины на 120 м.
Найдите площадь участка и выразите её в арах.
Многогранник изображённый на рисунке , составлен из кубов. Объём каждого куба равен 10 дм3. Вычислите объём многогранника.
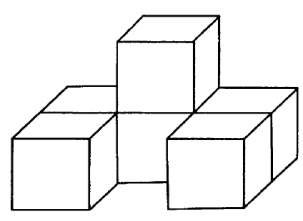
5. Из развёртки свернули куб. Нижняя грань куба заштрихована. Какая грань верхняя?
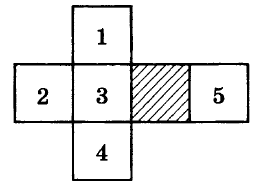
А. 1 ; Б. 2; В. 3; Г. 4; Д. 5.
6. Дан прямоугольный параллелепипед. Известны длины рёбер: АВ = 4см; AD = 5см, АК= 7см.
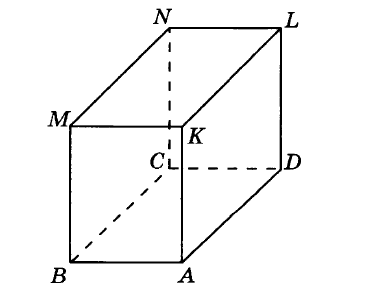
Запишите, чему равны длины рёбер:
А. ВМ = ______; Б. МК =______; В. МN = ______.
Вариант 2.
Найдите площадь квадрата, сторона которого равна 10 см.
Постройте две прямые, пересекающиеся под углом 600. Найдите остальные углы.
Длина прямоугольного участка земли 400 м, и она больше ширины на 140 м.
Найдите площадь участка и выразите её в арах.
Многогранник изображённый на рисунке, составлен из кубов. Объём каждого куба равен 5 дм3. Вычислите объём многогранника.

На каком из рисунков изображена развёртка данного кубика.
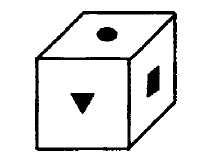
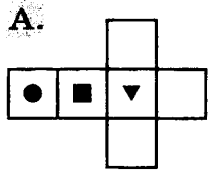
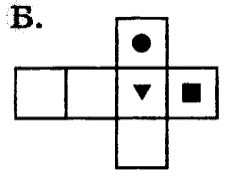
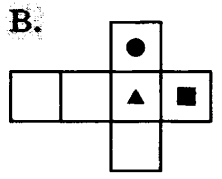
Дан прямоугольный параллелепипед. Известны длины рёбер: АВ = 3см; AD = 6см, АК= 4см. Запишите, чему равны длины рёбер:

А. ВМ = ______; Б. МК =______; В. МN = ______.
Контрольная работа «Окружность. Графы»
Вариант 1.
1. Вычислите длину окружности, радиус которой равен 6,5 дм.
2. Найдите площадь круга, радиус которого равен 4 см.
3. Длина окружности равна 31,4 см. Найдите площадь круга, радиус которого на 1 см больше радиуса данной окружности. (Число π ≈ 3,14).
4. Колесо на расстоянии 330 м сделало 100 оборотов. Найдите диаметр колеса. Результат округлите до сотых.
5. Вычислить площадь фигуры:
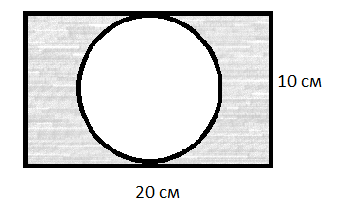
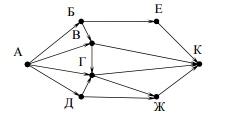
6.На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
Вариант 2.
1. Вычислите длину окружности, радиус которой равен 7,5 см.
2. Найдите площадь круга, радиус которого равен 8 дм.
3. Длина окружности равна 62,8 см. Найдите площадь круга, радиус которого в 2 раза меньше радиуса данной окружности. (Число π ≈ 3,14).
4. Колесо на расстоянии 380 м сделало 150 оборотов. Найдите диаметр колеса. Результат округлите до сотых.
5. Вычислить площадь фигуры:
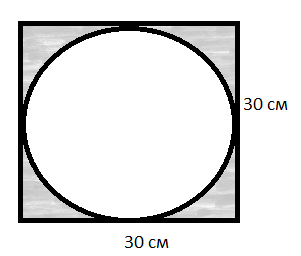
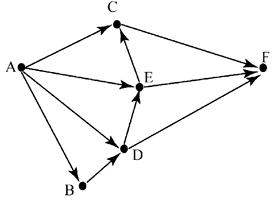
6.На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
Контрольная работа «Симметрия»
Вариант 1.
Нарисуйте паркет, используя фрагмент.
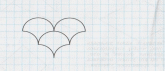
Лёня закрасил несколько клеточек на квадратном листке и сложил его по диагонали. Получился отпечаток.
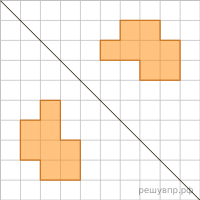
Затем на таком же листке Лёня закрасил несколько клеточек и тоже сложил листок по диагонали. Нарисуйте получившийся отпечаток.

Когда фигуру A повернули на 90° против часовой стрелки относительно точки О, получилась фигура В.
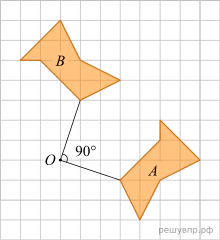
Нарисуйте фигуру, которая получится, если повернуть фигуру С на 90° против часовой стрелки относительно точки M.
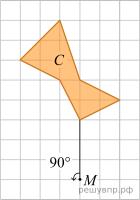
На рисунке 1 показаны фигуры, симметричные относительно точки О. На рисунке 2 показаны фигура и точка О. Нарисуйте фигуру, симметричную данной относительно точки О.


Рис. 1 Рис. 2
Вариант 2.
Задана часть бордюра и его оси симметрии. Продолжите бордюр.
Лёня закрасил несколько клеточек на квадратном листке и сложил его по диагонали. Получился отпечаток.

Затем на таком же листке Миша закрасил несколько клеточек и тоже сложил листок по диагонали. Нарисуйте получившийся отпечаток.

Когда фигуру A повернули на 90° против часовой стрелки относительно точки О, получилась фигура В.
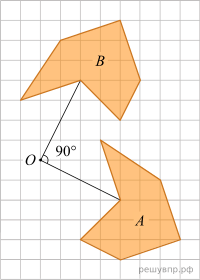
Нарисуйте фигуру, которая получится, если повернуть фигуру С на 90° против часовой стрелки относительно точки M.
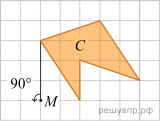
На рисунке 1 показаны фигуры, симметричные относительно точки О. На рисунке 2 показаны фигура и точка О. Нарисуйте фигуру, симметричную данной относительно точки О.


Рис. 1 Рис. 2
Контрольная работа «Площадь и объем»
Вариант 1.
Длина прямоугольного параллелепипеда 36 см, ширина в 4 раза меньше, а высота на 7 см больше ширины. Найдите объём прямоугольного параллелепипеда.
Объем прямоугольного параллелепипеда равен 420 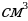 , длина – 12 см, ширина – 7 см. Найдите высоту данного параллелепипеда.
, длина – 12 см, ширина – 7 см. Найдите высоту данного параллелепипеда.
Постройте куб с ребром 2 см. Найдите площадь поверхности этого куба.
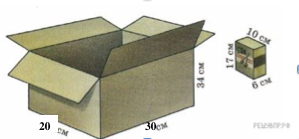
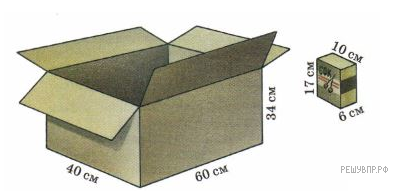
Сколько пакетов с соком войдёт в коробку, изображённую на рисунке?
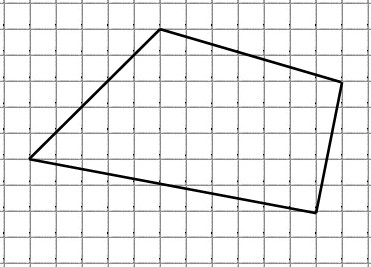
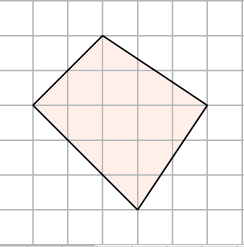
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Вариант 2.
Ширина прямоугольного параллелепипеда 24 см, длина в 4 раза больше, а высота на 5 см больше ширины. Найдите объём прямоугольного параллелепипеда.
Объем прямоугольного параллелепипеда равен 560 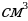 , длина – 14 см, ширина – 8 см. Найдите высоту данного параллелепипеда.
, длина – 14 см, ширина – 8 см. Найдите высоту данного параллелепипеда.
Постройте куб с ребром 3 см. Найдите площадь поверхности этого куба.
Сколько пакетов с соком войдёт в коробку, изображённую на рисунке?
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Контрольная работа «Координаты»
Вариант 1
Изобрази на координатной плоскости точки К(-2;4), М(4; 2), Е(2;-2), Р(-4;0). Соединив точки на чертеже, построй четырехугольник КМЕР. Найди координаты точки пересечения отрезков КЕ и МР.
Построй треугольник АВС, если А(0;3), В(-2;-3), С(4;0). Найди точки пересечения отрезка АВ с осью ОХ и отрезка ВС с осью ОУ.
Начерти треугольник КМР.
а) Измерь углы этого треугольника.
б) Проведи прямую, параллельную стороне КМ.
в) Проведи прямую, перпендикулярную стороне МР.
4. Начерти на координатной плоскости такую фигуру, абсцисса и ордината любой точки которой удовлетворяют условиям: 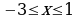 ,
, 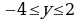 .
.
5. Чему равна площадь треугольника с вершинами А(2; 3), В(2; -2), С(-2; -2)?
Вариант 2
Изобрази на координатной плоскости точки А(2;4), В(5; 1), С(0;-4), К(-3;-1). Соединив точки на чертеже, построй четырехугольник АВСК. Найди координаты точки пересечения отрезков АС и ВК.
Построй треугольник МКР, если М(-3;5), К(3;0), Р(0;-5). Найди точки пересечения отрезка МР с осью ОХ и отрезка МК с осью ОУ.
Начерти треугольник АВС.
а) Измерь углы этого треугольника.
б) Проведи прямую, параллельную стороне АВ.
в) Проведи прямую, перпендикулярную стороне ВС.
Начерти на координатной плоскости такую фигуру, абсцисса и ордината любой точки которой удовлетворяют условиям: 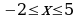 ,
, 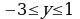 .
.
Найдите площадь прямоугольника с вершинами в точках А(-1; 1), В(3; 1), С(3; -2), D(-2; 1).
Промежуточная аттестация за 6 класс
Вариант 1.
Периметр прямоугольника 20 см, одна из его сторон 8 см. Найдите другую сторону прямоугольника, площадь и сторону квадрата, равновеликого данному прямоугольнику.
Найдите площадь фигуры.
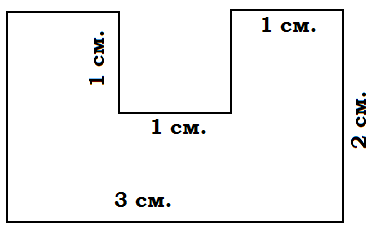


Найдите длину окружности с диаметром MN, если М(-2; 2), N(2; 2). Число 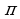 =3,14.
=3,14.
Вариант 2.
Периметр прямоугольника 40 см, одна из его сторон 18 см. Найдите другую сторону прямоугольника, площадь и сторону квадрата, равновеликого данному прямоугольнику.
Найдите площадь фигуры
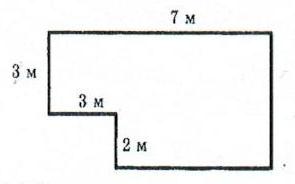

4.

5. Найдите длину окружности с диаметром MN, если М(-1; 2), N(3; 2). Число 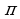 =3,14.
=3,14.
















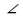 А=105о,
А=105о, 













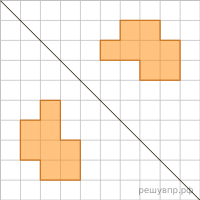










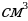 , длина – 12 см, ширина – 7 см. Найдите высоту данного параллелепипеда.
, длина – 12 см, ширина – 7 см. Найдите высоту данного параллелепипеда.



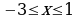 ,
, 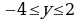 .
.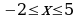 ,
, 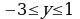 .
.


 =3,14.
=3,14.












