ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ИРКУТСКОЙ ОБЛАСТИ «ИРКУТСКИЙ КОЛЛЕДЖ АВТОМОБИЛЬНОГО ТРАНСПОРТА И ДОРОЖНОГО СТРОИТЕЛЬСТВА»
РАБОЧАЯ ТЕТРАДЬ
для выполнения практических работ
по дисциплине ОУД.05 Математика
для студентов 1 курса
Иркутск 2025г
Практическая работа № 1
| 1 вариант | 2 вариант |
| 1. Сократите дробь: а)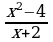 ; ;  б) б)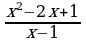 | 1. Сократите дробь: а)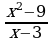 ; б) ; б)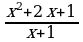 |
| 2. Упростите выражение: 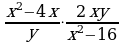 | 2. Упростите выражение: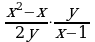 |
| 3. Решите уравнения: а)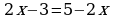 ; б) ; б)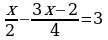 | 3. Решите уравнения: а)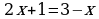 ; б) ; б)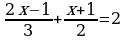 |
| 4. Решите систему линейных уравнений: а) 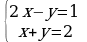 ; б) ; б)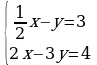 | 4. Решите систему линейных уравнений: а)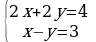 ; б) ; б)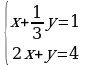 |
| 5. Решите уравнения: а)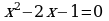 ; б) ; б) 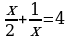 | 5. Решите уравнения: а)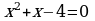 ; б) ; б)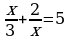 |
| 6. Решите неравенство: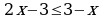 | 6. Решите неравенство: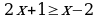 |
| 7. Решите систему неравенств: 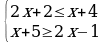
| 7. решите систему неравенств: 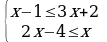
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Практическая работа № 2
| 1 вариант
| 2 вариант |
| 1. Решить уравнение: а)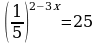 ; б) ; б)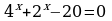 | 1. Решите уравнение: а)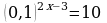 ; б) ; б)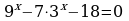 |
| 2. Решить неравенство: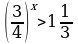 | 2. Решите неравенство: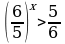 |
| 3. Решить систему уравнений: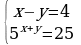 | 3. Решить систему уравнений: 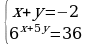
|
| _______________________________ | _______________________________ |
| 4. Решить неравенство: а)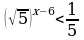 ; б) ; б)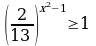 | 4. Решить неравенство: а)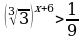 ; б) ; б)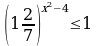  |
| 5. Решить уравнение: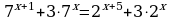 | 5. Решить уравнение: 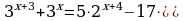 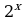
|
| 6. Решите уравнение: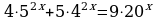 | 6. Решите уравнение: 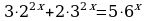
|
Практическая работа № 3
| 1 вариант
| 2 вариант |
| 1. Найдите значение выражения: а)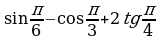 ; ; б)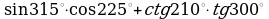 | 1. Найдите значение выражения: а)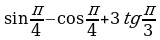 ; ; б)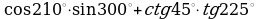 |
| 2. Вычислите: а)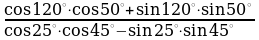 ; ; б)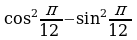 | 2. Вычислите: а)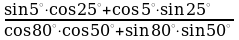 ; ; б)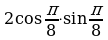 |
| 3. Упростите выражения: а)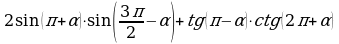 б) б)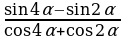 ; в) ; в)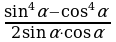 | 3. Упростите выражения: а)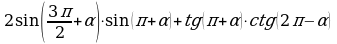 б) б)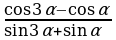 ; в) ; в) 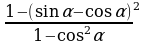  |
Доказать тождество: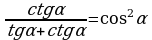 | 4. Доказать тождество: 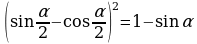
|
Практическая работа № 4
1 вариант
1. Найдите значение выражения: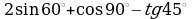
2. Сравните с нулем выражения: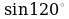 ;
; 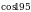 ;
; 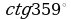 .
.
3. Вычислите: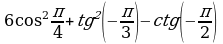
4. Упростите выражение: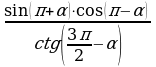
5. Упростите выражение: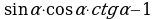
6. Упростите выражение: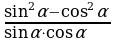
| 7. Вычислите: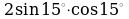 |
|
|
|
8. Вычислите: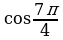
9. Представив 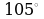 как
как 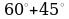 , вычислите
, вычислите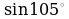
| 10. Дано: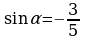 где где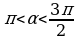 . Найдите . Найдите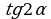 . . |
|
|
|
1. Найдите значение выражения: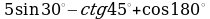
2. Сравните с нулем выражения: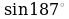 ;
; 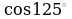 ;
; 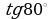
3. Вычислите: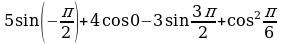
6. Упростите выражение: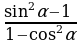
7. Вычислите: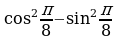
8. Вычислите: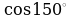
Практическая работа № 6
Тема: Тригонометрические уравнения.
1. Решите уравнения:
2. Решите уравнение, сделав подстановку:
| а)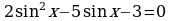 ; ; | б)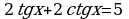 |
3. Решите уравнение методом разложения на множители:
| а)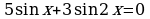 ; ; | б)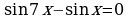
|
4. Решите уравнение, используя однородность:
| а)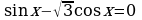 ; ; | б)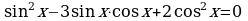 |
Решите уравнения:
2. Решите уравнение, сделав подстановку:
| а)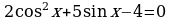 ; ; | б)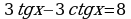 |
3. Решите уравнение, методом разложения на множители:
| а)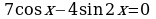 ; ; | б)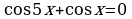 |
4. Решите уравнение, используя однородность:
| а)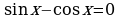 ; ; | б)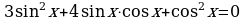 |
Практическая работа № 7
Тема: Производная.
1. Найдите производную функции:
| а)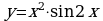 ; ; |
| в)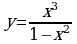 |
2. При движении тела по прямой, расстояние 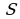 (в метрах) изменяется по закону
(в метрах) изменяется по закону 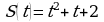 . Через сколько секунд после начала движения мгновенная скорость будет равна
. Через сколько секунд после начала движения мгновенная скорость будет равна 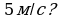
3. При каких значениях аргумента скорость изменения функции  равна скорости изменения функции
равна скорости изменения функции 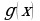 ?
?
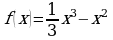 ;
; 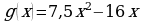
4. Построить график функции 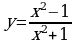 .
.
5. Найти наибольшее и наименьшее значения функции 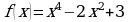 на отрезке
на отрезке 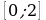 .
.
. Найдите производную функции
2. При движении тела по прямой, расстояние 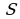 (в метрах) изменяется по закону
(в метрах) изменяется по закону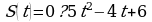 . Через сколько секунд после начала движения тело остановится?
. Через сколько секунд после начала движения тело остановится?
3. При каких значениях аргумента скорость изменения функции  равна скорости изменения функции
равна скорости изменения функции 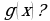
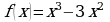 ;
; 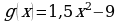
4. Построить график функции 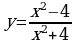 .
.
5.Найти наибольшее и наименьшее значения функции 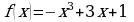 на отрезке
на отрезке 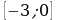 .
.
2. Тело движется по прямой по закону 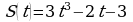 . В какой момент времени скорость тела будет равна
. В какой момент времени скорость тела будет равна 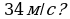
3. При каких значениях аргумента скорость изменения функции  равна скорости изменения функции
равна скорости изменения функции 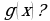
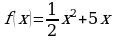 ;
; 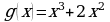
Практическая работа № 8
Тема: Первообразная и интеграл.
1. Определите функцию, для которой 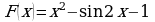 является первообразной:
является первообразной:
2. Для функции 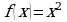 , найдите первообразную
, найдите первообразную 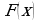 , принимающую заданное значение в заданной точке
, принимающую заданное значение в заданной точке 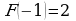 .
.
3. Точка движется по прямой так, что ее скорость в момент времени 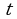 равна
равна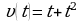 . Найдите путь, пройденный точкой за время от
. Найдите путь, пройденный точкой за время от 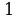 до
до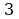 секунд, если скорость измеряется в
секунд, если скорость измеряется в 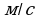 .
.
4. Вычислите: а)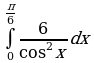 ; б)
; б)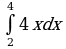
 .
.
5. Найдите площадь фигуры, ограниченной линиями:
1. Определите функцию, для которой 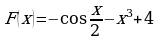 является первообразной:
является первообразной:
2. Для функции 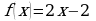 найдите первообразную
найдите первообразную 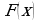 , график которой проходит через точку
, график которой проходит через точку 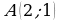 .
.
3. Точка движется по прямой так, что ее скорость в момент времени 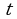 равна
равна 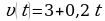 . Найдите путь, пройденный точкой за время от
. Найдите путь, пройденный точкой за время от 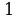 до
до 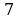 секунд, если измеряется в
секунд, если измеряется в 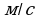 .
.
| 4. Вычислите: а)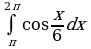 ; б) ; б)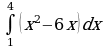 |
|
|
|
5. Найдите площадь фигуры, ограниченной линиями:
4. Вычислите: а)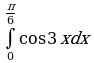 ; б)
; б)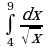
Практическая работа №9
Тема: Координаты вектора
1. Найти координаты, абсолютные величины векторов 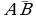 и
и 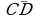 .
.
2. При каком значении 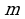 перпендикулярны векторы
перпендикулярны векторы 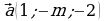 и
и 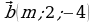 ?
?
3*. Проверьте, коллинеарные ли векторы 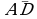 и
и 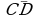 ?
?
4*. Образуют ли векторы 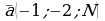 ,
, 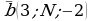 ,
, 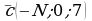 базис?
базис?
5**. Найти угол между векторами 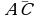 и
и 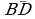 .
.
6**. Образуют ли векторы 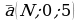 ,
, 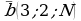 ,
, 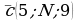 базис? Если да, то найти в нем координаты вектора
базис? Если да, то найти в нем координаты вектора 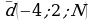 .
.
Практическая работа № 10
Тема: Многогранники.
Основанием прямой призмы ABCDA1B1C1D1 является параллелограмм ABCD со сторонами 6 см и 12 см и углом 60. Диагональ B1D призмы образует с плоскостью основания угол в 30. Найдите площадь полной поверхности призмы.
Сторона основания правильной треугольной пирамиды равна 3 см, а угол между боковой гранью и основанием равен 45. Найдите площадь полной поверхности пирамиды.
Сторона основания правильной треугольной пирамиды равна а, а боковая грань наклонена к плоскости основания под углом . Найдите площадь полной поверхности пирамиды.
Основанием прямой призмы ABCDA1B1C1D1 является параллелограмм ABCD со сторонами 4 см и 4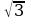 см и углом 30. Диагональ AC1 призмы образует с плоскостью основания угол в 60. Найдите площадь полной поверхности призмы.
см и углом 30. Диагональ AC1 призмы образует с плоскостью основания угол в 60. Найдите площадь полной поверхности призмы.
Высота основания правильной треугольной пирамиды равна 3 см, а угол между боковой гранью и основанием пирамиды равен 45. Найдите площадь полной поверхности пирамиды.
Основание пирамиды – квадрат со стороной а. Одна из боковых граней перпендикулярна основанию, а две смежные с ней грани составляют с плоскостью основания угол . Найдите площадь полной поверхности пирамиды.
Основанием прямой призмы ABCDA1B1C1D1 является параллелограмм ABCD со сторонами 6 см и 6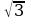 см и углом 150. Диагональ B1D призмы образует с плоскостью основания угол в 60. Найдите площадь полной поверхности призмы.
см и углом 150. Диагональ B1D призмы образует с плоскостью основания угол в 60. Найдите площадь полной поверхности призмы.
Сторона правильной треугольной пирамиды равна 4 см, а угол между боковым ребром и основанием равен 60. Найдите площадь полной поверхности пирамиды.
Высота правильной четырехугольной пирамиды равна H, а боковое ребро составляет с основанием угол . Найдите площадь полной поверхности пирамиды.
Практическая работа № 11
Тема: Тела вращения.
1. Осевое сечение цилиндра – квадрат, длина диагонали которого равна 20 см. Найдите радиус основания цилиндра.
2. Площадь осевого сечения цилиндра равна 6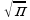 дм
дм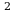 , а площадь основания цилиндра равна 25 дм
, а площадь основания цилиндра равна 25 дм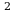 . Найдите высоту цилиндра.
. Найдите высоту цилиндра.
3. Длина образующей конуса равна 2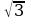 см, а угол при вершине осевого сечения конуса равен 120
см, а угол при вершине осевого сечения конуса равен 120 . Найдите площадь основания конуса.
. Найдите площадь основания конуса.
Радиус основания конуса 3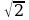 см. Найдите наибольшую возможную площадь осевого сечения данного конуса.
см. Найдите наибольшую возможную площадь осевого сечения данного конуса.
Стороны треугольника АВС касаются шара. Найдите радиус шара, если АВ =8 см, ВС=10 см, АС=12 см и расстояние от центра шара О до плоскости треугольника АВС равно 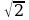 см.
см.
1. Осевое сечение цилиндра – квадрат, длина диагонали которого равна 36 см. Найдите радиус основания цилиндра.
2. Площадь осевого сечения цилиндра равна 12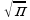 дм
дм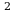 , а площадь основания равна 64дм
, а площадь основания равна 64дм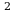 . Найдите высоту цилиндра.
. Найдите высоту цилиндра.
3. Высота конуса равна 4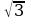 см, а угол при вершине осевого сечения конуса равен 120
см, а угол при вершине осевого сечения конуса равен 120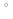 . Найдите площадь основания конуса.
. Найдите площадь основания конуса.
Радиус основания конуса равен 7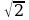 см. Найдите наибольшую возможную площадь осевого сечения данного конуса.
см. Найдите наибольшую возможную площадь осевого сечения данного конуса.
Стороны треугольника MKN касаются шара. Найдите радиус шара, если MK = 9 см, MN= 13 см, KN = 14 см и расстояние от центра шара О до плоскости MKN равно 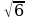 см.
см.







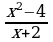 ;
;  б)
б)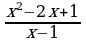
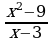 ; б)
; б)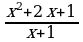
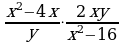
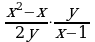
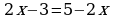 ; б)
; б)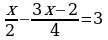
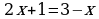 ; б)
; б)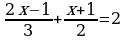
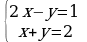 ; б)
; б)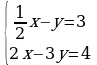
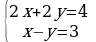 ; б)
; б)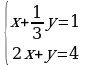
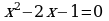 ; б)
; б) 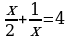
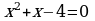 ; б)
; б)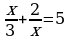
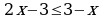
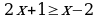
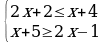
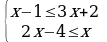
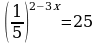 ; б)
; б)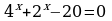
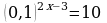 ; б)
; б)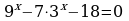
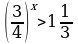
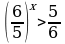
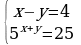
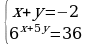
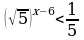 ; б)
; б)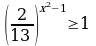
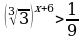 ; б)
; б)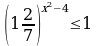
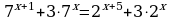
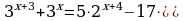
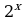
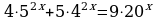
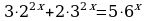
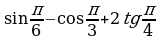 ;
; 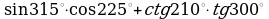
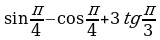 ;
;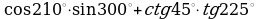
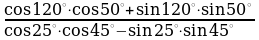 ;
;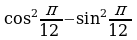
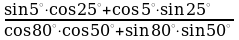 ;
;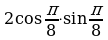
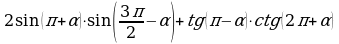 б)
б)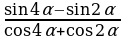 ; в)
; в)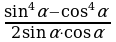
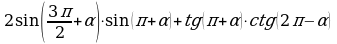 б)
б)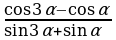 ; в)
; в)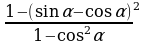
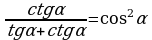
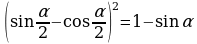
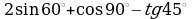
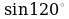 ;
; 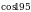 ;
; 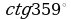 .
.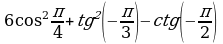
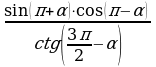
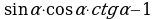
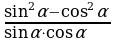
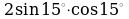
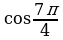
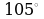 как
как 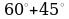 , вычислите
, вычислите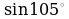
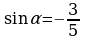 где
где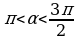 . Найдите
. Найдите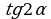 .
.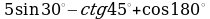
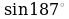 ;
; 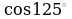 ;
; 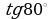
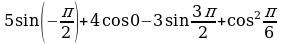
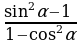
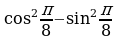
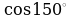
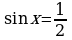 ;
;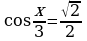 ;
;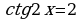 ;
;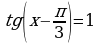
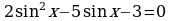 ;
;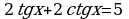
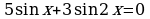 ;
;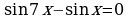
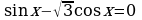 ;
;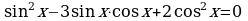
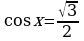 ;
;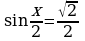 ;
; ;
;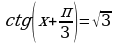
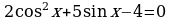 ;
;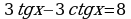
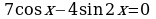 ;
;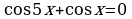
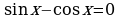 ;
;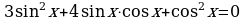
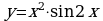 ;
;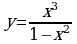
 (в метрах) изменяется по закону
(в метрах) изменяется по закону 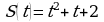 . Через сколько секунд после начала движения мгновенная скорость будет равна
. Через сколько секунд после начала движения мгновенная скорость будет равна 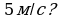
 равна скорости изменения функции
равна скорости изменения функции 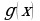 ?
?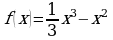 ;
; 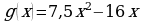
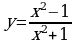 .
.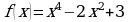 на отрезке
на отрезке 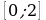 .
.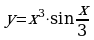 ;
;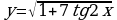 ;
;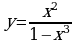
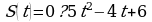 . Через сколько секунд после начала движения тело остановится?
. Через сколько секунд после начала движения тело остановится?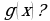
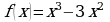 ;
; 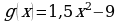
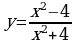 .
.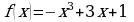 на отрезке
на отрезке 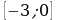 .
.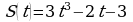 . В какой момент времени скорость тела будет равна
. В какой момент времени скорость тела будет равна 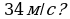
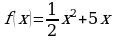 ;
; 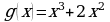
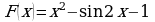 является первообразной:
является первообразной: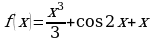 ;
;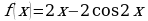 ;
;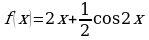 ;
;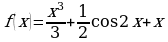
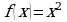 , найдите первообразную
, найдите первообразную 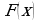 , принимающую заданное значение в заданной точке
, принимающую заданное значение в заданной точке 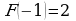 .
.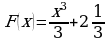 ;
;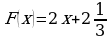 ;
;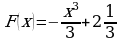 ;
;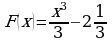
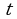 равна
равна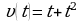 . Найдите путь, пройденный точкой за время от
. Найдите путь, пройденный точкой за время от 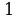 до
до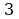 секунд, если скорость измеряется в
секунд, если скорость измеряется в 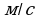 .
.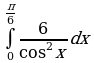 ; б)
; б)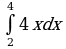
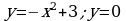
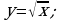
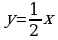
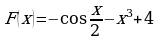 является первообразной:
является первообразной: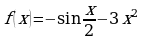 ;
;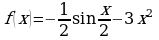 ;
;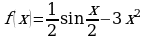 ;
;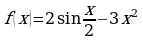 .
.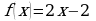 найдите первообразную
найдите первообразную 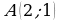 .
.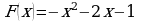
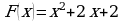 ;
;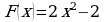
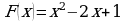
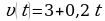 . Найдите путь, пройденный точкой за время от
. Найдите путь, пройденный точкой за время от 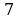 секунд, если измеряется в
секунд, если измеряется в 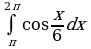 ; б)
; б)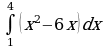
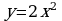 ;
; 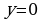 ;
; 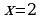
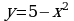 ;
; 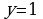 ;
; 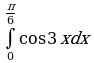 ; б)
; б)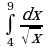
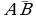 и
и 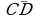 .
.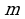 перпендикулярны векторы
перпендикулярны векторы 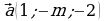 и
и 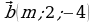 ?
? и
и 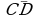 ?
?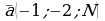 ,
, 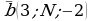 ,
, 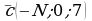 базис?
базис?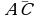 и
и 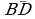 .
.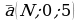 ,
, 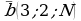 ,
, 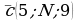 базис? Если да, то найти в нем координаты вектора
базис? Если да, то найти в нем координаты вектора 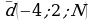 .
.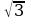 см и углом 30. Диагональ AC1 призмы образует с плоскостью основания угол в 60. Найдите площадь полной поверхности призмы.
см и углом 30. Диагональ AC1 призмы образует с плоскостью основания угол в 60. Найдите площадь полной поверхности призмы.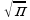 дм
дм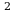 , а площадь основания цилиндра равна 25 дм
, а площадь основания цилиндра равна 25 дм . Найдите площадь основания конуса.
. Найдите площадь основания конуса.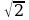 см. Найдите наибольшую возможную площадь осевого сечения данного конуса.
см. Найдите наибольшую возможную площадь осевого сечения данного конуса.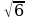 см.
см.









