муниципальное бюджетное образовательное учреждение
средняя общеобразовательная школа № 8
| Рассмотрено на МО учителей естественно- математического цикла, Протокол от 29. 08. 2019 г. №1 Руководитель МО __________ С.В.Казеева | Принято на заседании педагогического совета Протокол от 30.08.2019 г. №1 секретарь педсовета __________ Н. Е. Ефремова | Утверждаю Директор МБОУ СОШ №8 Приказ от 30.08.2019 г. №100 __________Е. А. Криницына |
РАБОЧАЯ УЧЕБНАЯ ПРОГРАММА
ПО АЛГЕБРЕ
ДЛЯ 8 КЛАССА
НА 2019-2020 УЧЕБНЫЙ ГОД
Программу составила: Бондарь Кира Евгеньевна
г. Красный Сулин
2019 г.
Пояснительная записка
Рабочая программа по алгебре в 8 классе составлена в соответствии со школьным Положением «О порядке разработки, рассмотрения и утверждения рабочих учебных программ, реализуемых школой», на основе Основной образовательной программы основного общего образования, примерной программы основного общего образования по алгебре для 7-9 классов (авторы: Ю. Н. Макарычев, К. И. Нешков, Н. Г. и др., составитель: Т. А. Бурмистрова).
Данная программа предполагает работу с учебником «Алгебра. 8 класс» (учеб. для учащихся общеобразоват. учреждений/ Ю. Н. Макарычев, К. И. Нешков, С. Б. Суворова; под редакцией С. А. Теляковского. 20-е изд., стер. – М.: Просвещение, 2011) и обеспечивает формирование всех типов мышления учащихся: логического, аналитического, конструктивного, алгоритмического и др.; развитие памяти, внимания, воображения; дает возможность пополнить запас историко-научных знаний школьников и сформировать у них представление о математике как части общечеловеческой культуры.
Курс алгебры 8 класса характеризуется повышением теоретического уровня обучения, постепенно усилением роли теоретических обобщений и дедуктивных заключений. Прикладная направленность курса обеспечивается систематическим обращением к примерам, раскрывающим возможности применения математики к изучению действительности и решению практических задач.
Цель курса: развитие вычислительных и формально – оперативных алгебраических умений до уровня, позволяющего уверенно использовать их при решении задач математики и смежных предметов; усвоение аппарата уравнений и неравенств как основного средства математического моделирования прикладных задач; осуществление функциональной подготовки школьников; овладение системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности каждому человеку в современном обществе, формирование и развитие средствами математики интеллектуальных качеств личности.
Цели обучения алгебре:
овладение базовым понятийным аппаратом по основным разделам содержания; представление об основных изучаемых понятиях как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления;
умение работать с математическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, проводить классификации, логические обоснования, доказательства математических утверждений;
овладение навыками устных, письменных, инструментальных вычислений;
овладение языком алгебры;
умение выразить на языке алгебры процессы, происходящие в окружающем мире.
умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочных материалов, калькулятора, компьютера.
овладение системой математических знаний и умений, необходимых в практической деятельности, продолжения образования; приобретение опыта планирования и осуществления алгоритмической деятельности;
Место предмета в учебном плане
Учебный план МБОУ СОШ №8 включает обязательное изучение алгебры в 8 классе из расчета 4 часа в неделю.
В соответствии с годовым учебным графиком, расписанием учебных занятий, с учетом государственных праздников, рабочая учебная программа составлена из расчета 4 часа в неделю, 135 часов в год.
Содержание программы
Повторение курса алгебры 7 класса.
Повторение основных понятий, определений, формул курса алгебры 7 класса.
Рациональные дроби.
Рациональная дробь. Основное свойство дроби, сокращение дробей. Сумма и разность дробей. Произведение и частное дробей. Преобразования рациональных выражений. Функция  и ее график.
и ее график.
Цель: выработать умение выполнять тождественные преобразования рациональных выражений.
Так как действия с рациональными дробями существенным образом опираются на действия с многочленами, то в начале темы необходимо повторить с учащимися преобразования целых выражений.
Главное место в данной теме занимают алгоритмы действий с дробями. Учащиеся должны понимать, что сумму, разность, произведение и частное дробей всегда можно представить в виде дроби. Приобретаемые в данной теме умения выполнять сложение, вычитание, умножение и деление дробей являются опорными в преобразованиях дробных выражений. Поэтому им следует уделить особое внимание. Нецелесообразно переходить к комбинированным заданиям на все действия с дробями прежде, чем будут усвоены основные алгоритмы. Задания на все действия с дробями не должны быть излишне громоздкими и трудоемкими.
При нахождении значений дробей даются задания на вычисления с помощью калькулятора. В данной теме расширяются сведения о статистических характеристиках. Вводится понятие среднего гармонического ряда положительных чисел.
Изучение темы завершается рассмотрением свойств графика функции  .
.
Квадратные корни.
Понятие об иррациональных числах. Общие сведения о действительных числах. Квадратный корень. Арифметический квадратный корень. Уравнение х2=а. Понятие о нахождении приближенного значения квадратного корня. Свойства квадратных корней. Преобразования выражений, содержащих квадратные корни. Функция  ее свойства и график.
ее свойства и график.
Цель: систематизировать сведения о рациональных числах и дать представление об иррациональных числах, расширив тем самым понятие о числе; выработать умение выполнять преобразования выражений, содержащих квадратные корни.
В данной теме учащиеся получают начальное представление о понятии действительного числа. С этой целью обобщаются известные учащимся сведения о рациональных числах. Для введения понятия иррационального числа используется интуитивное представление о том, что каждый отрезок имеет длину и потому каждой точке координатной прямой соответствует некоторое число.
При введении понятия корня полезно ознакомить учащихся с нахождением корней с помощью калькулятора.
Основное внимание уделяется понятию арифметического квадратного корня и свойствам арифметических квадратных корней. Доказываются теоремы о корне из произведения и дроби, а также тождество  , которые получают применение в преобразованиях выражений, содержащих квадратные корни. Специальное внимание уделяется освобождению от иррациональности в знаменателе дроби в выражениях вида
, которые получают применение в преобразованиях выражений, содержащих квадратные корни. Специальное внимание уделяется освобождению от иррациональности в знаменателе дроби в выражениях вида 
 . Умение преобразовывать выражения, содержащие корни, часто используется как в самом курсе алгебры, так и в курсах геометрии, алгебры и начал анализа.
. Умение преобразовывать выражения, содержащие корни, часто используется как в самом курсе алгебры, так и в курсах геометрии, алгебры и начал анализа.
Продолжается работа по развитию функциональных представлений учащихся. Рассматриваются функция  , ее свойства и график. При изучении функции
, ее свойства и график. При изучении функции  показывается ее взаимосвязь с функцией
показывается ее взаимосвязь с функцией  , где x ≥ 0.
, где x ≥ 0.
Квадратные уравнения.
Квадратные уравнения. Формула корней квадратного уравнения. Теорема Виета. Решение задач, приводящих к квадратным уравнениям и простейшим рациональным уравнениям. Дробные рациональные уравнения.
Цель: выработать умения решать квадратные уравнения и простейшие рациональные уравнения и применять их к решению задач.
В начале темы приводятся примеры решения неполных квадратных уравнений. Этот материал систематизируется. Рассматриваются алгоритмы решения неполных квадратных уравнений различного вида.
Основное внимание следует уделить решению уравнений вида ах2 + bх + с = 0, где а ≠ 0, с использованием формулы корней. В данной теме учащиеся знакомятся с формулами Виета, выражающими связь между корнями квадратного уравнения и его коэффициентами. Они используются в дальнейшем при доказательстве теоремы о разложении квадратного трехчлена на линейные множители.
Учащиеся овладевают способом решения дробных рациональных уравнений, который состоит в том, что решение таких уравнений сводится к решению соответствующих целых уравнений с последующим исключением посторонних корней.
Изучение данной темы позволяет существенно расширить аппарат уравнений, используемых для решения текстовых задач.
Неравенства.
Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Погрешность и точность приближения. Пересечение и объединение множеств. Числовые промежутки. Линейные неравенства с одной переменной и их системы.
Цель: ознакомить учащихся с применением неравенств для оценки значений выражений, выработать умение решать линейные неравенства с одной переменной и их системы.
Свойства числовых неравенств составляют ту базу, на которой основано решение линейных неравенств с одной переменной. Теоремы о почленном сложении и умножении неравенств находят применение при выполнении простейших упражнений на оценку выражений по методу границ. Вводятся понятия абсолютной погрешности и точности приближения, относительной погрешности.
Умения проводить дедуктивные рассуждения получают развитие как при доказательствах указанных теорем, так и при выполнении упражнений на доказательства неравенств.
В связи с решением линейных неравенств с одной переменной дается понятие о числовых промежутках, вводятся соответствующие названия и обозначения. Рассмотрению систем неравенств с одной переменной предшествует ознакомление учащихся с понятиями пересечения и объединения множеств.
При решении неравенств используются свойства равносильных неравенств, которые разъясняются на конкретных примерах. Особое внимание следует уделить отработке умения решать простейшие неравенства вида ах b, ах b, остановившись специально на случае, где а 0.
В этой теме рассматривается также решение систем двух линейных неравенств с одной переменной, в частности таких, которые записаны в виде двойных неравенств.
Степень с целым показателем. Элементы статистики.
Определение степени с целым отрицательным показателем. Степень с целым показателем и ее свойства. Стандартный вид числа. Элементы статистики. Сбор и группировка статистических данных. Наглядное представление статистической информации.
Цель: выработать умение применять свойства степени с целым показателем в вычислениях и преобразованиях.
В этой теме формулируются свойства степени с целым показателем. Метод доказательства этих свойств показывается на примере умножения степеней с одинаковыми основаниями. Дается понятие о записи числа в стандартном виде. Приводятся примеры использования такой записи в физике, технике и других областях знаний.
Рассматриваются элементы статистики.
Итоговое повторение курса алгебры 8 класса
Закрепление знаний, умений и навыков, полученных на уроках по данным темам (курс алгебры 8 класса).
Учебно-тематический план
| Тема | Общее количество часов | Кол-во часов на контрольные работы |
| Повторение курса алгебры 7 класса. | 5 | 1 |
Рациональные дроби. | 31 | 2 |
Квадратные корни. | 29 | 2 |
Квадратные уравнения. | 25 | 2 |
Неравенства. | 32 | 2 |
Степень с целым показателем. Элементы статистики. | 10 | 1 |
| Итоговое повторение курса алгебры 8 класса. | 3 | 1 |
| ИТОГО: | 135 | 10 |
Планируемые результаты
Рациональные числа
Ученик научится:
понимать особенности десятичной системы счисления;
владеть понятиями, связанными с делимостью натуральных чисел;
выражать числа в эквивалентных формах, выбирая наиболее подходящую в зависимости от конкретной ситуации;
сравнивать и упорядочивать рациональные числа;
выполнять вычисления с рациональными числами, сочетая устные и письменные приёмы вычислений, применение калькулятора;
использовать понятия и умения, связанные с пропорциональностью величин, процентами в ходе решения математических задач и задач из смежных предметов, выполнять несложные практические расчёты.
Ученик получит возможность:
1) познакомиться с позиционными системами счисления с основаниями, отличными от 10;
2) углубить и развить представления о натуральных числах и свойствах делимости;
3) научиться использовать приёмы, рационализирующие вычисления, приобрести привычку контролировать вычисления, выбирая подходящий для ситуации способ.
Действительные числа
Ученик научится:
1)использовать начальные представления о множестве действительных чисел;
2)владеть понятием квадратного корня, применять его в вычислениях.
Ученик получит возможность:
1) развить представление о числе и числовых системах от натуральных до действительных чисел; о роли вычислений в человеческой практике;
2) развить и углубить знания о десятичной записи действительных чисел (периодические и непериодические дроби).
Измерения, приближения, оценки
Ученик научится:
1)находить приближенные значения квадратного корня;
2) использовать в ходе решения задач элементарные представления, связанные с приближёнными значениями величин, погрешность и точность приближения.
Ученик получит возможность:
1)понять, что числовые данные, которые используются для характеристики объектов окружающего мира, являются преимущественно приближёнными, что по записи приближённых значений, содержащихся в информационных источниках, можно судить о погрешности приближения;
2)понять, что погрешность результата вычислений должна быть соизмерима с погрешностью исходных данных.
Алгебраические выражения
Ученик научится:
1) выполнять алгебраические действия над рациональными дробями;
2) выполнять преобразования выражений, содержащих степени с натуральными и целыми показателями, квадратные корни;
3) выполнять тождественные преобразования алгебраических выражений, разложение многочленов на множители;
4)выполнять тождественные преобразования рациональных выражений на основе правил действий над многочленами и алгебраическими дробями.
Ученик получит возможность:
1) научиться выполнять многошаговые преобразования рациональных выражений, применяя широкий набор способов и приёмов;
2) применять тождественные преобразования для решения текстовых и нетекстовых задач.
Уравнения
Ученик научится:
1) решать квадратные уравнения, дробные рациональные уравнения;
2) понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных реальных ситуаций, решать текстовые задачи алгебраическим методом;
Ученик получит возможность:
1) овладеть специальными приёмами решения уравнений; уверенно применять аппарат уравнений для решения разнообразных задач из математики, смежных предметов, практики.
Неравенства
Ученик научится:
1)понимать и применять терминологию и символику, связанные с отношением неравенства, свойства числовых неравенств;
2)решать линейные неравенства с одной переменной и их системы.
Ученик получит возможность научиться:
1)разнообразным приёмам доказательства неравенств; уверенно применять аппарат неравенств для решения разнообразных математических задач и задач из смежных предметов, практики.
Числовые функции
Ученик научится:
1) понимать и использовать функциональные понятия и язык (термины, символические обозначения);
2) строить графики элементарных функцийнн; исследовать свойства числовых функций на основе изучения поведения их графиков;
3) понимать функцию как важнейшую математическую модель для описания процессов и явлений окружающего мира, применять функциональный язык для описания и исследования зависимостей между физическими величинами.
Ученик получит возможность научиться:
1) проводить исследования, связанные с изучением свойств функций, в том числе с использованием компьютера.
2)использовать функциональные представления и свойства функций для решения математических задач из различных разделов курса.
Элементы статистики
Ученик научится:
1)использовать простейшие способы представления и анализа статистических данных.
Ученик получит возможность:
1) приобрести первоначальный опыт организации сбора данных при проведении опроса общественного мнения, осуществлять их анализ, представлять результаты опроса, например, в виде таблицы, гистограммы, диаграммы.
В результате освоения курса алгебры 8 класса учащиеся должны овладеть следующими знаниями, умениями, навыками.
Личностным результатом изучения предмета является формирование следующих умений и качеств:
Независимость и критичность мышления;
Воля и настойчивость в достижении цели.
Метапредметными результатами изучения курса является формирование универсальных учебных действий (УУД).
Регулятивные УУД:
Самостоятельно обнаруживать и формулировать учебную проблему, определять цель УД;
Выдвигать версии решения проблемы, осознавать (и интерпретировать в случае необходимости) конечный результат, выбирать средства достижения цели из предложенных, а также искать их самостоятельно;
Составлять (индивидуально или в группе) план решения проблемы (выполнения проекта);
Работая по плану, сверять свои действия с целью и при необходимости исправлять ошибки самостоятельно (в том числе и корректировать план);
В диалоге с учителем совершенствовать самостоятельно выбранные критерии оценки.
Познавательные УУД:
Проводить наблюдение и эксперимент под руководством учителя;
Осуществлять расширенный поиск информации с использованием ресурсов библиотек и Интернета;
Осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий;
Анализировать, сравнивать, классифицировать и обобщать факты и явления;
Давать определения понятиям.
Коммуникативные УУД:
Самостоятельно организовывать учебное взаимодействие в группе (определять общие цели, договариваться друг с другом и т.д.);
В дискуссии уметь выдвинуть аргументы и контраргументы;
Учиться критично относиться к своему мнению, с достоинством признавать ошибочность своего мнения и корректировать его;
Понимая позицию другого, различать в его речи: мнение (точку зрения), доказательство (аргументы), факты (гипотезы, аксиомы, теории).
Личностные, метапредметные и предметные результаты
освоения содержания курса
Программа позволяет добиваться следующих результатов освоения образовательной программы основного общего образования:
личностные:
ответственного отношения к учению, готовности и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию;
формирования коммуникативной компетентности в общении и сотрудничестве со сверстниками, старшими и младшими в образовательной, учебно-исследовательской, творческой и других видах деятельности;
умения ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
первоначального представления о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации;
критичности мышления, умения распознавать логически некорректные высказывания, отличать гипотезу от факта;
креативности мышления, инициативы, находчивости, активности при решении арифметических задач;
умения контролировать процесс и результат учебной математической деятельности;
формирования способности к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
метапредметные:
способности самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
умения осуществлять контроль по образцу и вносить необходимые коррективы;
способности адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения;
умения устанавливать причинно-следственные связи; строить логические рассуждения, умозаключения (индуктивные, дедуктивные и по аналогии) и выводы;
умения создавать модели и схемы для решения учебных и познавательных задач;
развития способности организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников, взаимодействовать и находить общие способы работы; умения работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов; слушать партнёра; формулировать, аргументировать и отстаивать своё мнение;
формирования компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентностй);
первоначального представления об идеях и о методах математики как об универсальном языке науки и техники;
развития способности видеть математическую задачу в других дисциплинах, в окружающей жизни;
умения находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
умения понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
умения выдвигать гипотезы при решении учебных задач и понимания необходимости их проверки;
понимания сущности алгоритмических предписаний и умения действовать в соответствии с предложенным алгоритмом;
умения самостоятельно ставить цели, выбирать и создавать алгоритмы для рещения учебных математических проблем;
способности планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
предметные:
умения работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику, использовать различные языки математики (словесный, символический, графический), развития способности обосновывать суждения, проводить классификацию;
владения базовым понятийным аппаратом: иметь представление о числе, владение символьным языком алгебры, знание элементарных функциональных зависимостей, формирование представлений о статистических закономерностях в реальном мире и различных способах их изучения;
умения выполнять арифметические преобразования рациональных выражений, применять их для решения учебных математических задач и задач, возникающих в смежных учебных предметах;
умения пользоваться изученными математическими формулами и самостоятельно составлять формулы зависимостей между величинами на основе обобщения частных случаев и эксперимента;
уметь решать линейные, квадратные, дробные рациональные уравнения, неравенства, системы;
овладение системой функциональных понятий, функциональным языком и символикой, умение строить графики функций, описывать их свойства, использовать функционально-графические представления для описания и анализа математических задач и реальных зависимостей;
знания основных способов представления и анализа статистических данных;
умения применять изученные понятия, результаты и методы при решении задач из различных разделов курса, в том числе задач, не сводящихся к непосредственному применению известных алгоритмов.
ФГОС выдвигает особые требования к подготовке обучающихся к жизни - сегодня важно вооружить их не столько знаниями, сколько способами овладения ими. Учитель должен научить детей учиться, научить находить полезную для них информацию, которая способствовала бы развитию мировоззрения, кругозора, культуры личности учащихся. Именно интернет зарекомендовал себя в современном мире, как главный источник информации, однако информации разного качества, даже киберугроз. Поэтому, учителю, важно обращать внимание учащихся на правила кибербезопасности: вводить персональные данные только на государственных сайтах; соблюдать конфиденциальность; не использовать онлайн-сервисы для хранения паролей; проверить какой-либо факт или информацию, можно обратившись к «Википедии» (данный сайт хорошо себя зарекомендовал и считается безопасным по версии https://www.ucheba.ru/project/websafety); не нужно делать в интернете ничего, что бы вы не стали бы делать в физическом мире. Разница между виртуальной и реальной действительностью минимальна
Календарно-тематическое планирование.
Алгебра.
8 класс.
Количество часов в неделю – 4 ч
Количество часов за год – 135 ч
(поурочное планирование)
| № урока | Дата проведения | Тема урока | Кол-во часов | Виды деятельности на уроке |
| по плану | по факту |
| Повторение курса алгебры 7 класса. (5 часов) |
| 1. | 03.09. |
| Повторение курса алгебры 7 класса. Линейная функция. Степень с натуральным показателем. | 1 | Повторить, обобщить и систематизировать знания и умения учащихся в преобразовании выражений, решении уравнений с одной переменной, решении систем линейных уравнений с двумя переменными, решении текстовых и нетекстовых задач, умении строить график (линейной) функции и работать с ним, умении работать со степенями, содержащими натуральный показатель, выполнять действия над многочленами, преобразовывать целые выражения и др. |
| 2. | 04.09. |
| Повторение курса алгебры 7 класса. Многочлены. Формулы сокращённого умножения. | 1 |
| 3. | 05.09. |
| Повторение курса алгебры 7 класса. Системы линейных уравнений. | 1 |
| 4. | 06.09. |
| Повторение курса алгебры 7 класса. Решение задач и уравнений. | 1 |
| 5. | 10.09. |
| Диагностическая контрольная работа. | 1 |
| Глава 1. Рациональные дроби. (31 час) |
| 6. | 11.09. |
| Рациональные выражения. | 1 |
Формулировать основное свойство рациональной дроби и применять его для преобразования дробей.
Выполнять сложение, вычитание рациональных дробей (сложение и вычитание дробей с одинаковыми и разными знаменателями).
Выполнять различные преобразования рациональных выражений, доказывать тождества. |
| 7. | 12.09. |
| Решение упражнений по теме «Рациональные выражения». | 1 |
| 8. | 13.09. |
| Основное свойство дроби. Сокращение дробей. | 1 |
| 9. | 17.09. |
| Решение упражнений по теме «Основное свойство дроби. Сокращение дробей». | 1 |
| 10. | 18.09. |
| Основное свойство дроби. Сокращение дробей. Закрепление. | 1 |
| 11. | 19.09. |
| Сложение и вычитание дробей с одинаковыми знаменателями. | 1 |
| 12. | 20.09. |
| Решение упражнений по теме «Сложение и вычитание дробей с одинаковыми знаменателями». | 1 |
| 13. | 24.09. |
| Сложение и вычитание дробей с одинаковыми знаменателями. Закрепление. | 1 |
| 14. | 25.09. |
| Сложение и вычитание дробей с разными знаменателями. | 1 |
| 15. | 26.09. |
| Решение упражнений по теме «Сложение и вычитание дробей с разными знаменателями». | 1 |
| 16. | 27.09. |
| Сложение и вычитание дробей с разными знаменателями. Закрепление. | 1 |
| 17. | 01.10. |
| Обобщающий урок «Рациональные выражения. Сокращение дробей. Сложение и вычитание дробей». | 1 |
| 18. | 02.10. |
| Контрольная работа № 1 «Рациональные дроби и их свойства. Сумма и разность дробей.» | 1 |
| 19. | 03.10. |
| Анализ контрольной работы. | 1 |
| 20. | 04.10. |
| Умножение дробей. | 1 |
Выполнять умножение и деление рациональных дробей, а также возведение дроби в степень.
Выполнять различные преобразования рациональных выражений, доказывать тождества.
Знать свойства функции у=k/x, где k ≠ 0, и уметь строить её график.
Использовать компьютер для исследования положения графика в координатной плоскости в зависимости от k. |
| 21. | 08.10. |
| Решение упражнений по теме «Умножение дробей». | 1 |
| 22. | 09.10. |
| Возведение дроби в степень. | 1 |
| 23. | 10.10. |
| Решение упражнений по теме «Возведение дроби в степень». | 1 |
| 24. | 11.10. |
| Умножение дробей. Возведение дроби в степень. Закрепление. | 1 |
| 25. | 15.10. |
| Деление дробей. | 1 |
| 26. | 16.10. |
| Решение упражнений по теме «Деление дробей». | 1 |
| 27. | 17.10. |
| Деление дробей. Закрепление. | 1 |
| 28. | 18.10. |
| Преобразование рациональных выражений. | 1 |
| 29. | 22.10. |
| Решение упражнений по теме «Преобразование рациональных выражений». | 1 |
| 30. | 23.10. |
| Упрощение выражений с применением преобразований рациональных выражений. | 1 |
| 31. | 24.10. |
| Функция у = k / х и ее график. | 1 |
| 32. | 25.10. |
| Построение графика функция у = k / x. Свойства функции у = k / x. | 1 |
| 33. | 05.11. |
| Решение упражнений по теме « Функция у = k / х и ее график». | 1 |
| 34. | 06.11. |
| Представление дроби в виде суммы дробей. | 1 |
| 35. | 07.11. |
| Контрольная работа № 2 «Произведение и частное дробей. Функция у = k / х и ее график.» | 1 |
| 36. | 08.11. |
| Анализ контрольной работы. | 1 |
| Глава 2. Квадратные корни. (29 часов) |
| 37. | 12.11. |
| Рациональные числа. | 1 |
Приводить примеры рациональных и иррациональных чисел.
Находить значения арифметических квадратных корней, используя при необходимости калькулятор.
Доказывать теоремы о корне из произведения и дроби, тождество  , применять их в преобразованиях выражений. , применять их в преобразованиях выражений.
Строить график функции y =  и иллюстрировать на графике её свойства. и иллюстрировать на графике её свойства.
Освобождаться от иррациональности в знаменателях дробей вида  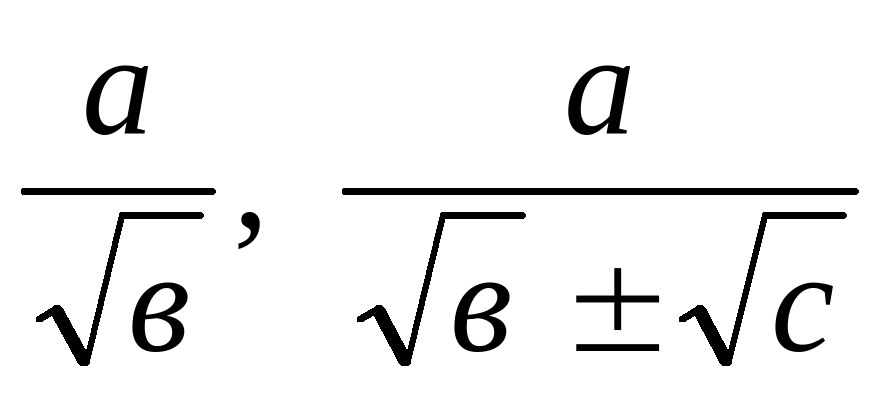 . .
.
Выносить множитель за знак корня и вносить множитель под знак корня.
Использовать квадратные корни для выражения переменных из геометрических и физических формул.
|
| 38. | 13.11. |
| Решение упражнений по теме «Рациональные числа». | 1 |
| 39. | 14.11. |
| Иррациональные числа. | 1 |
| 40. | 15.11. |
| Решение упражнений по теме «Иррациональные числа». | 1 |
| 41. | 19.11. |
| Квадратные корни. Арифметический квадратный корень. | 1 |
| 42. | 20.11. |
| Решение упражнений по теме «Квадратные корни. Арифметический квадратный корень». | 1 |
| 43. | 21.11. |
| Квадратные корни. Арифметический квадратный корень. Закрепление. | 1 |
| 44. | 22.11. |
| Уравнение х2 = а. | 1 |
| 45. | 26.11. |
| Решение упражнений по теме « х2 = а». | 1 |
| 46. | 27.11. |
| Нахождение приближенных значений квадратного корня. | 1 |
| 47. | 28.11. |
| Функция у = √х и ее график. | 1 |
| 48. | 29.11. |
| Функция у = √х и ее свойства. | 1 |
| 49. | 03.12. |
| Свойства и график функции у = √х. Закрепление. | 1 |
| 50. | 04.12. |
| Квадратный корень из произведения. | 1 |
| 51. | 05.12. |
| Квадратный корень из дроби. | 1 |
|
52. | 06.12. |
| Квадратный корень из произведения и дроби. | 1 |
| 53. | 10.12. |
| Квадратный корень из степени. | 1 |
| 54. | 11.12. |
| Решение упражнений по теме « Квадратный корень из степени». | 1 |
| 55. | 12.12. |
| Обобщающий урок «Квадратные корни». | 1 |
| 56. | 13.12. |
| Контрольная работа № 3 «Действительные числа. Арифметический квадратный корень и его свойства.». | 1 |
| 57. | 17.12. |
| Анализ контрольной работы. | 1 |
| 58. | 18.12. |
| Вынесение множителя за знак корня. | 1 |
| 59. | 19.12. |
| Внесение множителя под знак корня. | 1 |
| 60. | 20.12. |
| Преобразование выражений, содержащих квадратные корни. | 1 |
| 61. | 24.12. |
| Решение упражнений по теме «Преобразование выражений, содержащих квадратные корни». | 1 |
| 62. | 25.12. |
| Преобразование выражений, содержащих квадратные корни. Закрепление. | 1 |
| 63. | 26.12. |
| Преобразование двойных радикалов. | 1 |
| 64. | 27.12. |
| Контрольная работа № 4 «Применение свойств арифметического квадратного корня». | 1 |
| 65. | 14.01. |
| Анализ контрольной работы. | 1 |
| Глава 3. Квадратные уравнения. (25 часов) |
| 66. | 15.01. |
| Неполные квадратные уравнения. | 1 |
Решать квадратные уравнения.
Решать задачи с помощью квадратных уравнений.
Находить подбором корни квадратного уравнения, используя теорему Виета.
Исследовать квадратные уравнения по дискриминанту и коэффициентам. |
| 67. | 16.01. |
| Решение неполных квадратных уравнений. | 1 |
| 68. | 17.01. |
| Неполные квадратные уравнения. Закрепление. | 1 |
| 69. | 21.01. |
| Формула корней квадратного уравнения. | 1 |
| 70. | 22.01. |
| Решение квадратных уравнений по формуле. | 1 |
| 71. | 23.01. |
| Формула корней квадратного уравнения для квадратных уравнений с четным вторым коэффициентом. | 1 |
| 72. | 24.01. |
| Решение квадратных уравнений. | 1 |
| 73. | 28.01. |
| Решение квадратных уравнений. Закрепление. | 1 |
| 74. | 29.01. |
| Обобщающий урок «Квадратные уравнения». | 1 |
| 75. | 30.01. |
| Решение задач с помощью квадратных уравнений. | 1 |
| 76. | 31.01. |
| Решение задач с помощью квадратных уравнений. Закрепление. | 1 |
| 77. | 04.02. |
| Теорема Виета. | 1 |
| 78. | 05.02. |
| Решение квадратных уравнений, используя теорему Виета. | 1 |
| 79. | 06.02. |
| Обобщающий урок «Квадратные уравнения. Решение задач с помощью квадратных уравнений». | 1 |
| 80. | 07.02. |
| Контрольная работа № 5 «Квадратные уравнения». | 1 |
| 81. | 11.02. |
| Анализ контрольной работы. | 1 |
| 82. | 12.02. |
| Дробные рациональные уравнения. | 1 |
Решать дробные рациональные уравнения, сводя решение таких уравнений к решению линейных и квадратных уравнений с последующим исключением посторонних корней.
Решать текстовые задачи, используя квадратные и дробные уравнения. |
| 83. | 13.02. |
| Решение дробных рациональных уравнений. | 1 |
| 84. | 14.02. |
| Решение дробных рациональных уравнений. Закрепление. | 1 |
| 85. | 18.02. |
| Обобщающий урок «Решение дробных рациональных уравнений». | 1 |
| 86. | 19.02. |
| Решение задач с помощью рациональных уравнений. | 1 |
| 87. | 20.02. |
| Решение задач с помощью рациональных уравнений. Закрепление. | 1 |
| 88. | 21.02. |
| Уравнения с параметром. | 1 |
| 89. | 25.02. |
| Контрольная работа № 6 «Дробные рациональные уравнения» | 1 |
| 90. | 26.02. |
| Анализ контрольной работы. | 1 |
| Глава 4. Неравенства. (32 часа) |
| 91. | 27.02. |
| Числовые неравенства. | 1 |
Формулировать и доказывать свойства числовых неравенств.
. |
| 92. | 28.02. |
| Решение упражнений по теме «Числовые неравенства». | 1 |
| 93. | 03.03. |
| Числовые неравенства. Закрепление. | 1 |
| 94. | 04.03. |
| Свойства числовых неравенств. | 1 |
| 95. | 05.03. |
| Решение упражнений по теме «Свойства числовых неравенств». | 1 |
| 96. | 06.03. |
| Свойства числовых неравенств. Закрепление. | 1 |
| 97. | 10.03. |
| Сложение числовых неравенств. | 1 |
| 98. | 11.03. |
| Умножение числовых неравенств. | 1 |
| 99. | 12.03. |
| Сложение и умножение числовых неравенств. | 1 |
| 100 | 13.03. |
| Обобщающий урок «Числовые неравенства и их свойства». | 1 |
| 101 | 17.03. |
| Контрольная работа № 7 «Числовые неравенства и их свойства». | 1 |
| 102 | 18.03. |
| Анализ контрольной работы. | 1 |
| 103 | 19.03. |
| Погрешность и точность приближения. | 1 |
Использовать аппарат неравенств для оценки погрешности и точности приближения.
Находить пересечение и объединение множеств, в частности числовых промежутков.
Решать линейные неравенства.
Решать системы линейных неравенств, в том числе таких, которые записаны в виде двойных неравенств. |
| 104 | 20.03. |
| Абсолютная и относительная погрешности. | 1 |
| 105 | 01.04. |
| Пересечение и объединение множеств. | 1 |
| 106 | 02.04. |
| Числовые промежутки. | 1 |
| 107 | 03.04. |
| Решение упражнений по теме «Числовые промежутки». | 1 |
| 108 | 07.04. |
| Числовые промежутки. Закрепление. | 1 |
| 109 | 08.04. |
| Неравенства с одной переменной. | 1 |
| 110 | 09.04. |
| Свойства, используемые при решении неравенств с одной переменной. | 1 |
| 111 | 10.04. |
| Решение неравенств с одной переменной. | 1 |
| 112 | 14.04. |
| Решение неравенств с одной переменной. Закрепление. | 1 |
| 113 | 15.04. |
| Обобщающий урок «Решение неравенств с одной переменной». | 1 |
| 114 | 16.04. |
| Системы неравенств с одной переменной. | 1 |
| 115 | 17.04. |
| Решение систем неравенств с одной переменной. | 1 |
| 116 | 21.04. |
| Решение систем неравенств с одной переменной. Закрепление. | 1 |
| 117 | 22.04. |
| Двойные неравенства. | 1 |
| 118 | 23.04. |
| Решение двойных неравенств. | 1 |
| 119 | 24.04. |
| Решение двойных неравенств. Закрепление. | 1 |
| 120 | 28.04. |
| Доказательство неравенств. | 1 |
| 121 | 29.04. |
| Контрольная работа № 8 «Неравенства с одной переменной и их системы» | 1 |
| 122 | 30.04. |
| Анализ контрольной работы. | 1 |
| Глава 5. Степень с целым показателем. Элементы статистики. (10 часов) |
| 123 | 05.05. |
| Определение степени с целым отрицательным показателем. | 1 |
Знать определение и свойства степени с целым показателем.
Применять свойства степени с целым показателем при выполнении вычислений и преоб- разовании выражений.
Использовать запись чисел в стандартном виде для выражения и сопоставления размеров объектов, длительности процессов в окружающем мире. Приводить примеры репрезентативной и нерепрезентативной выборки.
Извлекать информацию из таблиц частот и организовывать информацию в виде таблиц частот, строить интервальный ряд.
Использовать наглядное представление статистической информации в виде столбчатых и круговых диаграмм, полигонов, гистограмм.
|
| 124 | 06.05. |
| Решение упражнений по теме «Степень с целым отрицательным показателем». | 1 |
| 125 | 07.05. |
| Свойства степени с целым показателем. | 1 |
| 126 | 08.05. |
| Решение упражнений по теме «Свойства степени с целым показателем». | 1 |
| 127 | 13.05. |
| Стандартный вид числа. | 1 |
| 128 | 14.05. |
| Представление числа в стандартном виде. | 1 |
| 129 | 15.05. |
| Обобщающий урок «Степень с целым показателем» | 1 |
| 130 | 19.05. |
| Контрольная работа № 9 «Степень с целым показателем» | 1 |
| 131 | 20.05. |
| Анализ контрольной работы. Сбор и группировка статистических данных. | 1 |
| 132 | 21.05. |
| Наглядное представление статистической информации. | 1 |
|
Итоговое повторение курса алгебры 8 класса. (3 часа) |
| 133 | 22.05. |
| Итоговое повторение курса алгебры 8 класса. | 1 |
Обобщение, коррекция и систематизация знаний и умений. Контроль знаний и умений. |
| 134 | 26.05. |
| Итоговая контрольная работа. | 1 |
| 135 | 27.05. |
| Итоговый урок. | 1 |

















