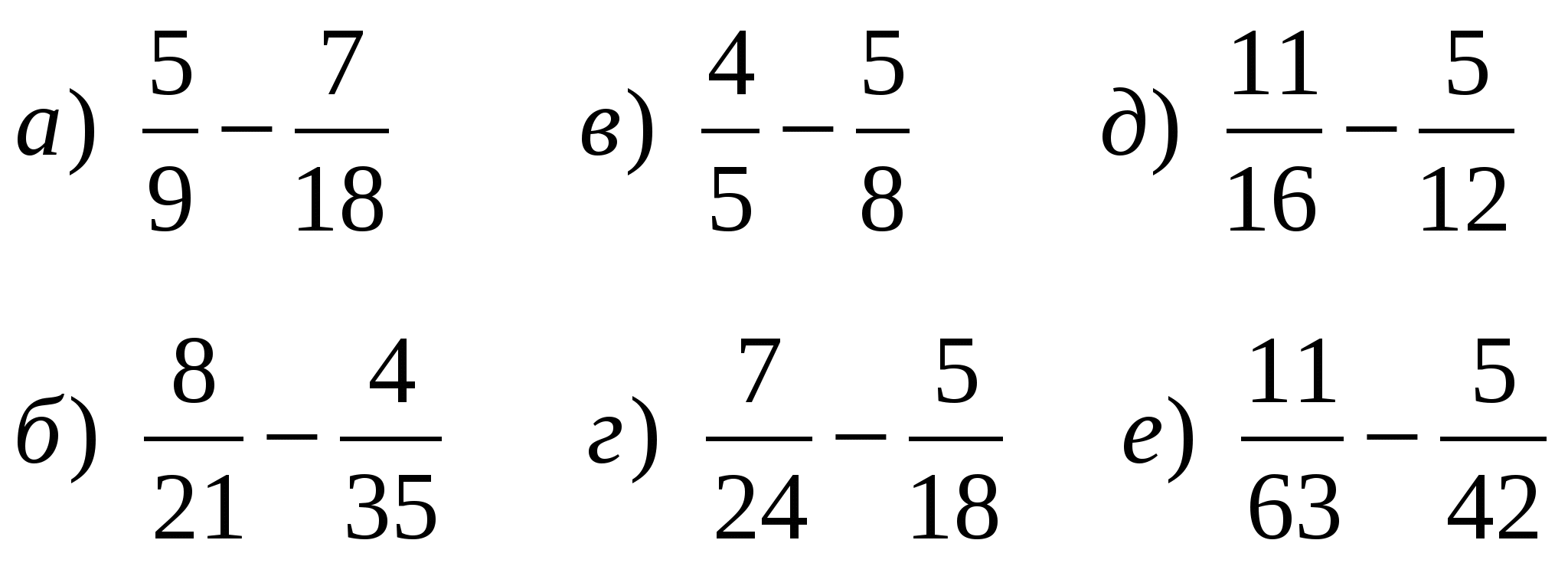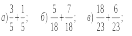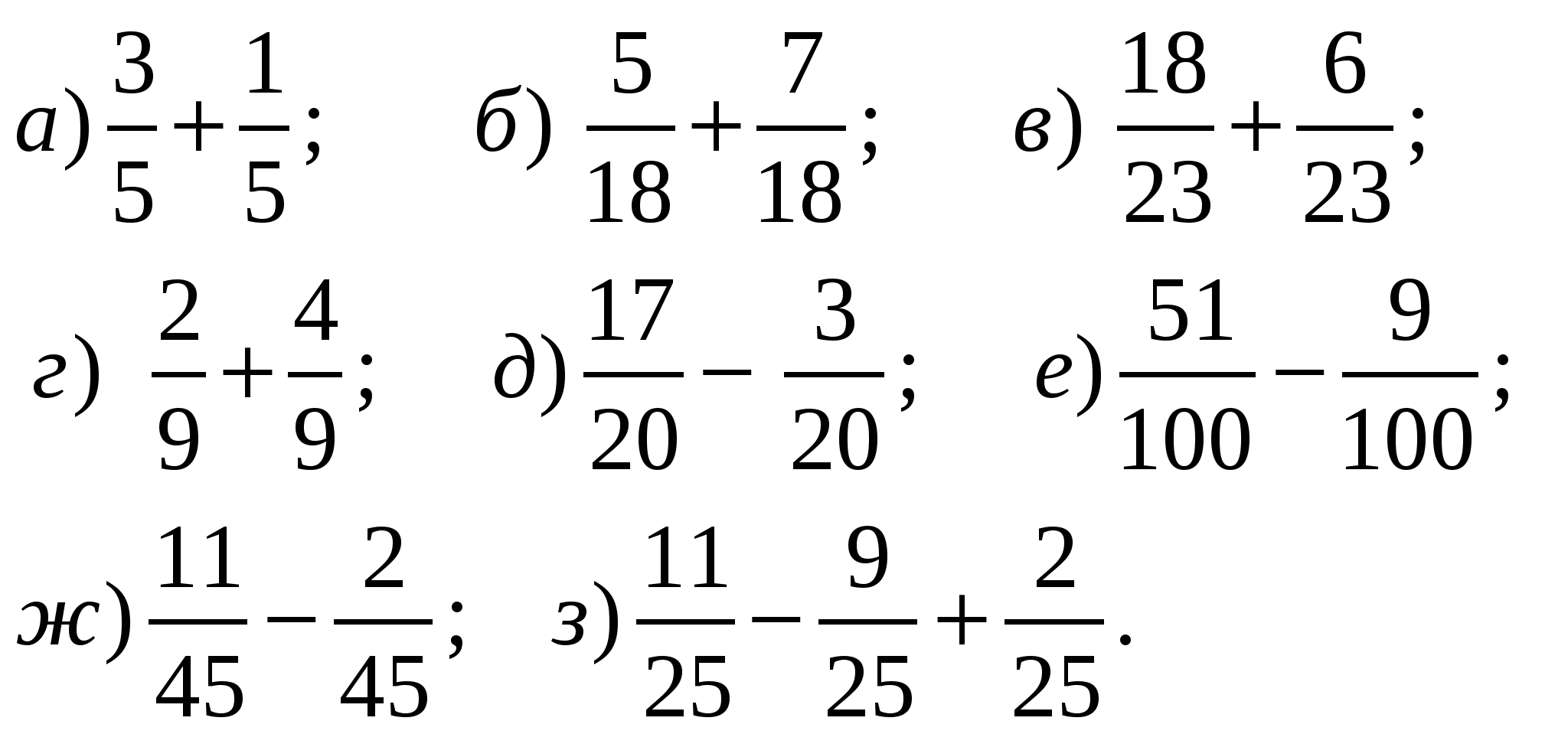Данная разработка предназначена для учащихся 5-6 классов для отработки или закрепления навыков сложения, вычитания, приведения к общему знаменателю и применение основного свойства дроби. Содержит как теоретический, так и практический материал, а также домашнее задание. Рекомендуемое время для реализации два урока, соответственно домашнее задание также можно разбить на две части.
Просмотр содержимого документа
«Рабочий лист для отработки действий с обыкновенными дробями»
Свойства дробей
Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:
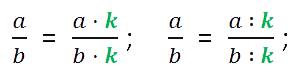 где a, b, k — натуральные числа.
где a, b, k — натуральные числа.
Основные свойства
Дробь не имеет значения, если знаменатель равен нулю.
Дробь равна нулю, если числитель равен нулю, а знаменатель — нет.
Две дроби a/b и c/d называются равными, если a * d = b * c.
Пример:

Задание 1. Заполните пробелы:
Сокращение дробей
Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число.
| Пример 1 | Пример 2 | Пример 3 |
| 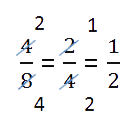
| 
| 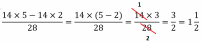
|
Задание 2. Сократите дроби:
Сравнение дробей
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.
Задание 3. Сравните дроби
Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю.
Задание 4. Сравните дроби
Сложение и вычитание дробей
П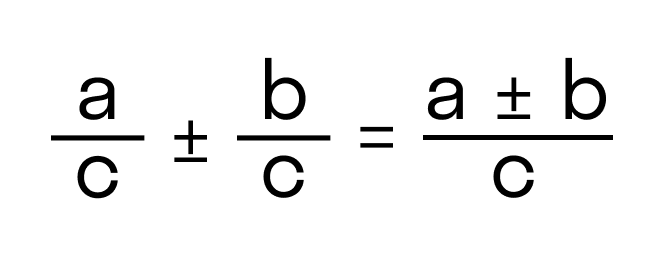 ри сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.
ри сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.
Не забудьте проверить, можно ли сократить дробь и выделить целую часть.
Задание 5. Вычислите (если надо, сократите/выделите целую часть):
При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).
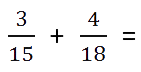
Вот, что делать:
Н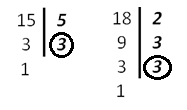 айдем наименьшее общее кратное для определения единого делителя. Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.
айдем наименьшее общее кратное для определения единого делителя. Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.
НОК (15, 18) = 3 * 2 * 3 * 5 = 90
Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:
9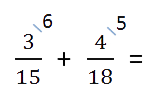 0 : 15 = 6,
0 : 15 = 6,
90 : 18 = 5.
Полученные числа запишем справа сверху над числителем.
Воспользуемся одним из основных свойств дробей: перемножим числитель и знаменатель на дополнительный множитель. После умножения знаменатель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.
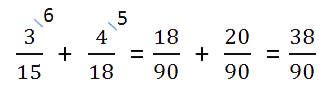
Проверим полученный результат:
если числитель больше знаменателя, нужно преобразовать дробь в смешанное число;
если есть что сократить, нужно выполнить сокращение.
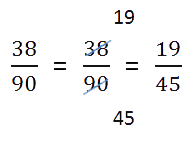
 Задание 6. Вычислите (если надо, сократите/выделите целую часть):
Задание 6. Вычислите (если надо, сократите/выделите целую часть):
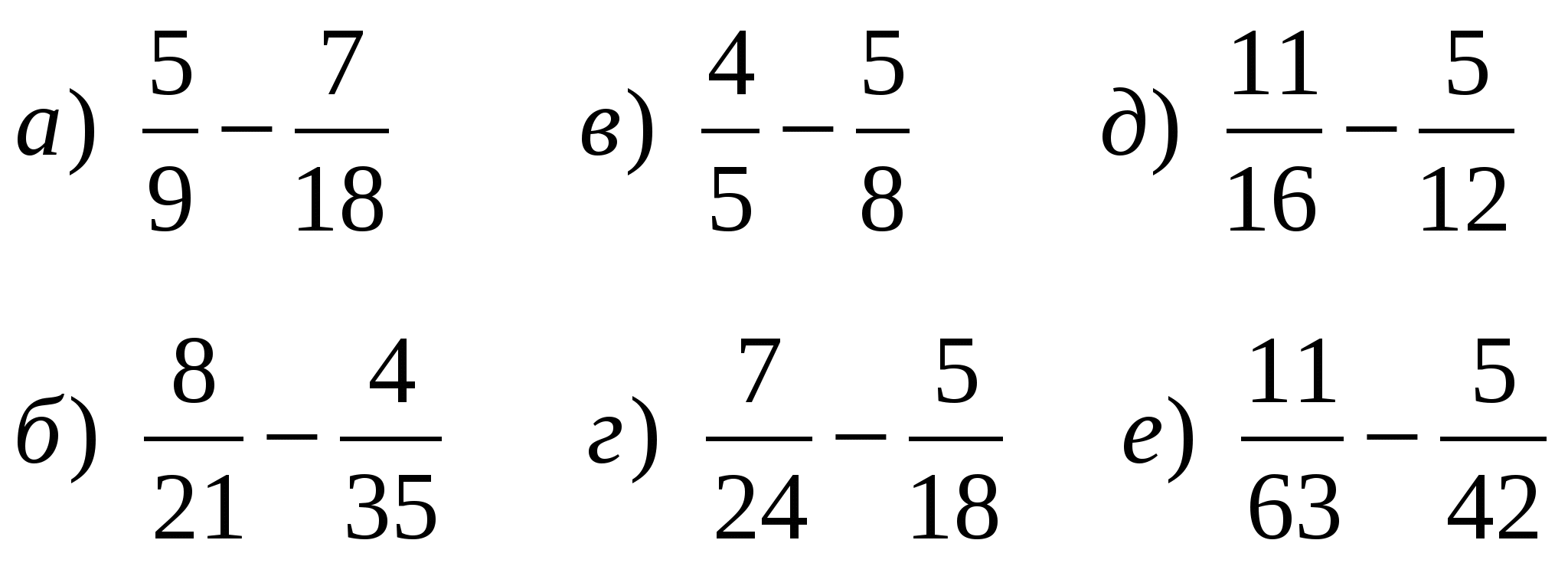
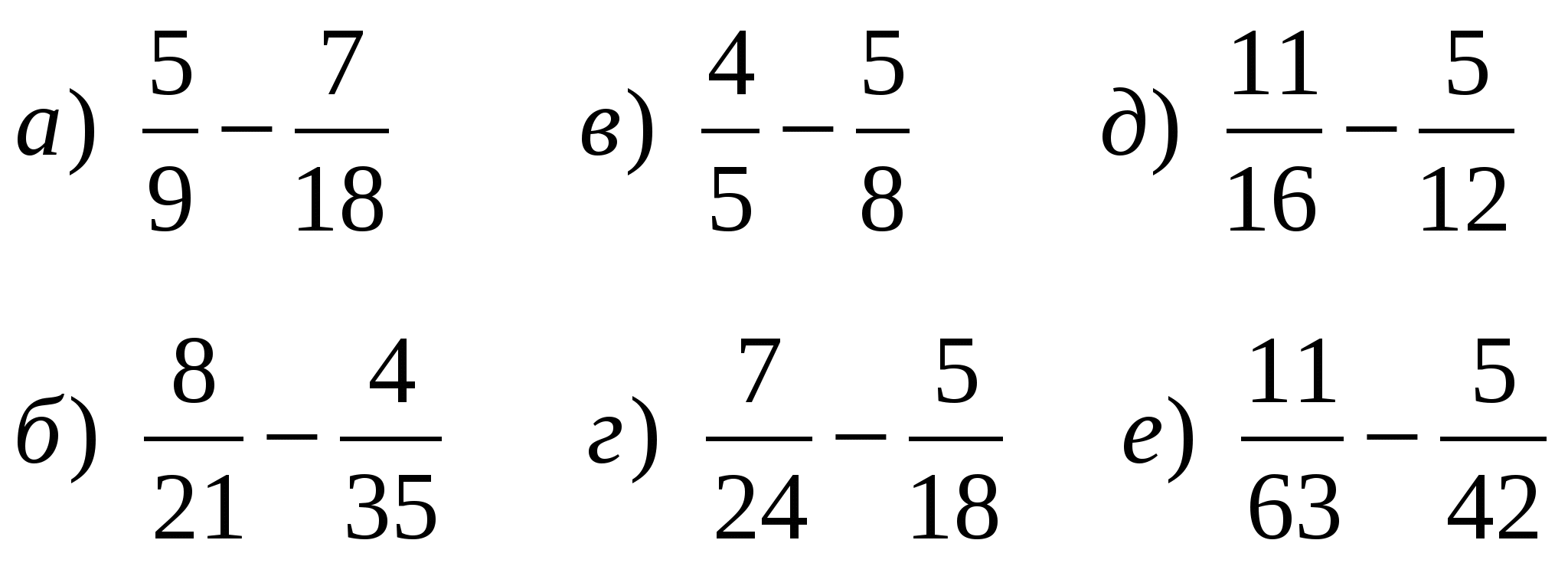
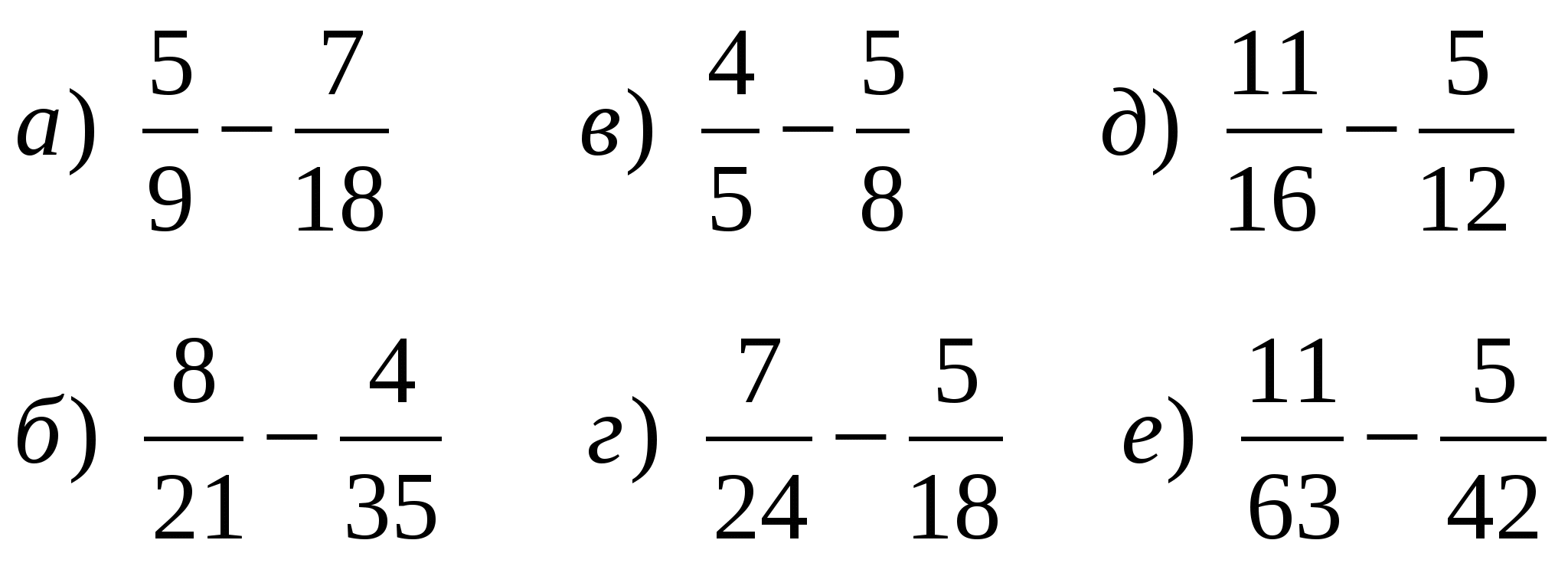
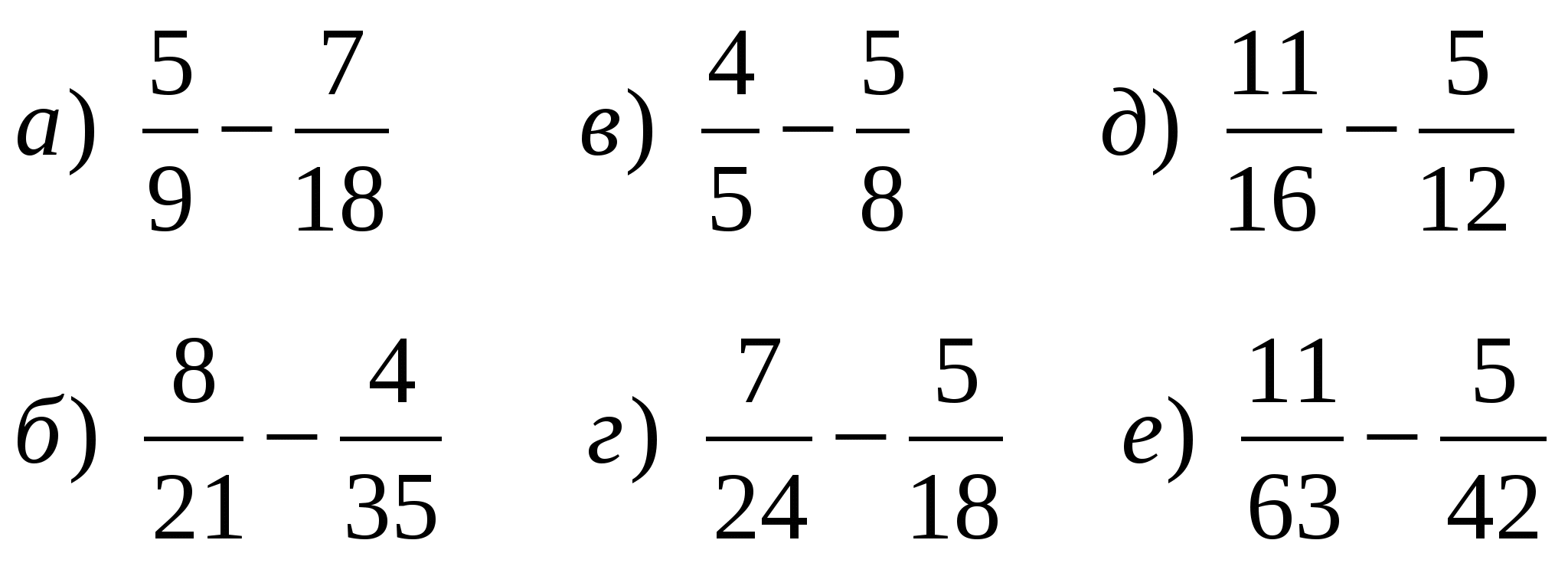
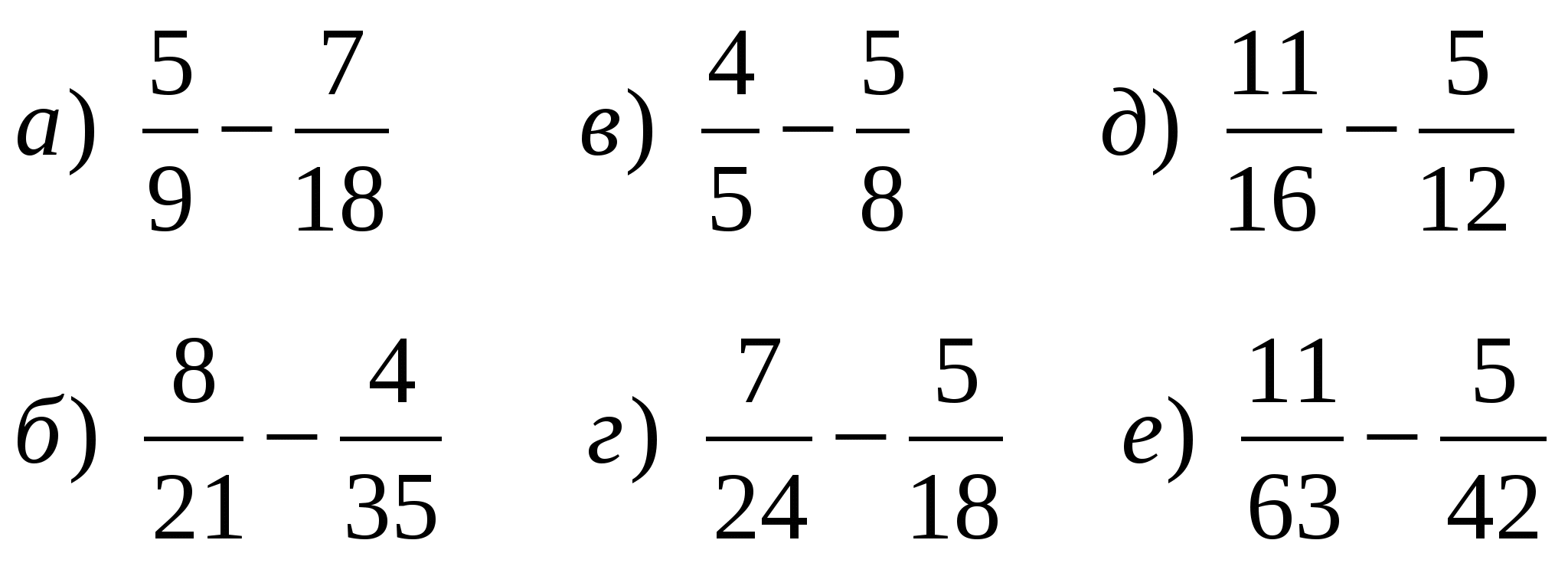
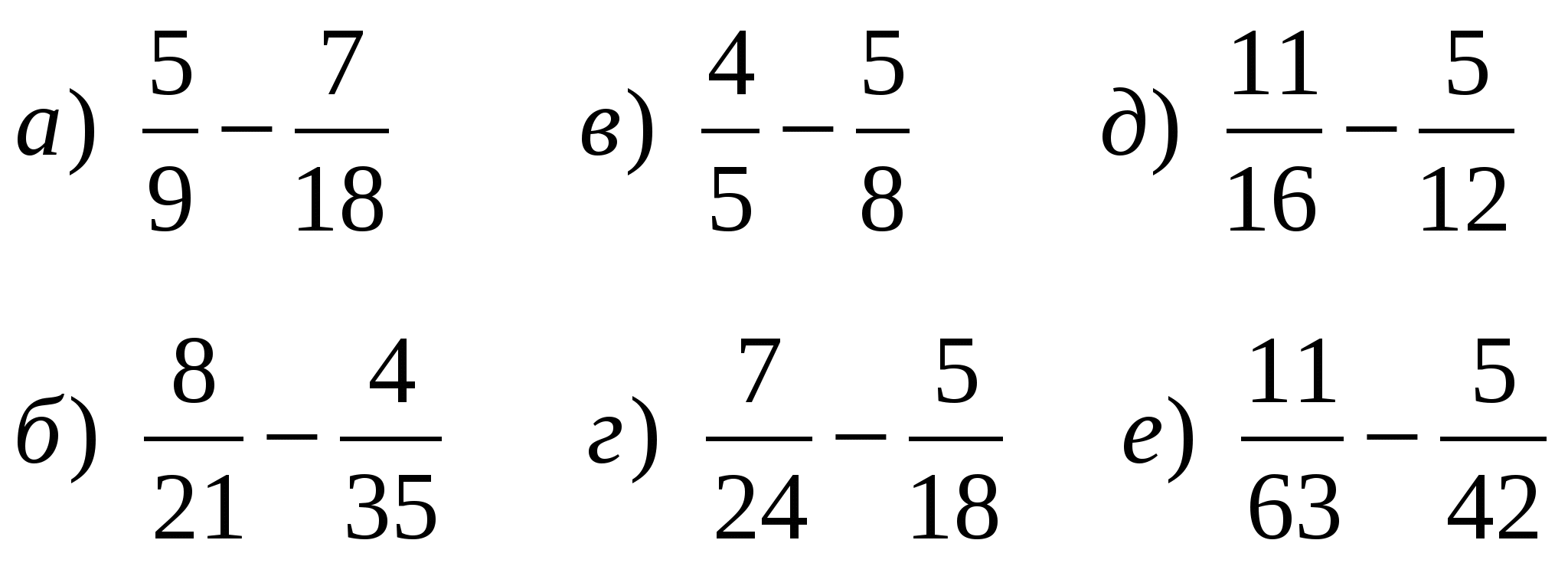
Домашнее задание
№1.
| 1) Умножьте на 4 числитель и знаменатель каждой из дробей: |
| 1 | ; |
| 2 | ; |
| 7 | ; |
| 11 | ; |
|
|
|
|
|
|
|
|
|
|
| 2 |
| 4 |
| 7 |
| 10 |
|
|
|
|
|
|
|
|
|
|
| 2) Разделите на 5 числитель и знаменатель каждой из дробей: |
| 5 | ; |
| 15 | ; |
| 30 | ; |
| 55 | ; |
|
|
|
|
|
|
|
|
|
|
|
| 10 |
| 20 |
| 35 |
| 55 |
|
|
|
|
|
|
|
|
|
|
|
| 3) Пользуясь основным свойством дроби, заполните пропуски: |
|
| = | 8 | ; |
|
| = | 30 | ; |
| 7 | = |
|
|
|
|
|
|
|
| 7 | 28 |
| 9 | 45 |
| 12 | 48 |
|
|
|
|
|
|
№2.
| 1) Сократите дробь: |
| 7 | ; |
| 5 | ; |
| 20 | ; |
| 46 | ; |
| 120 |
|
|
|
|
|
| 14 |
| 25 |
| 60 |
| 80 |
| 1300 |
|
|
|
|
|
| 2) Сократите: |
| 24×8 | ; | 5×3×3×6 | ; | 6×18 - 10×6 |
|
|
|
|
|
|
| 16×42 | 3×2×15×6 | 66 |
|
|
|
|
|
|
№3.
| 1) Сравните дроби: |
| 2 | и | 4 | ; |
| 9 | и | 27 | ; |
| 25 | и | 13 |
|
|
|
|
|
| 4 | 10 |
| 30 | 70 |
| 28 | 14 |
|
|
|
|
|
№4. Вычислите:
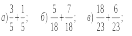
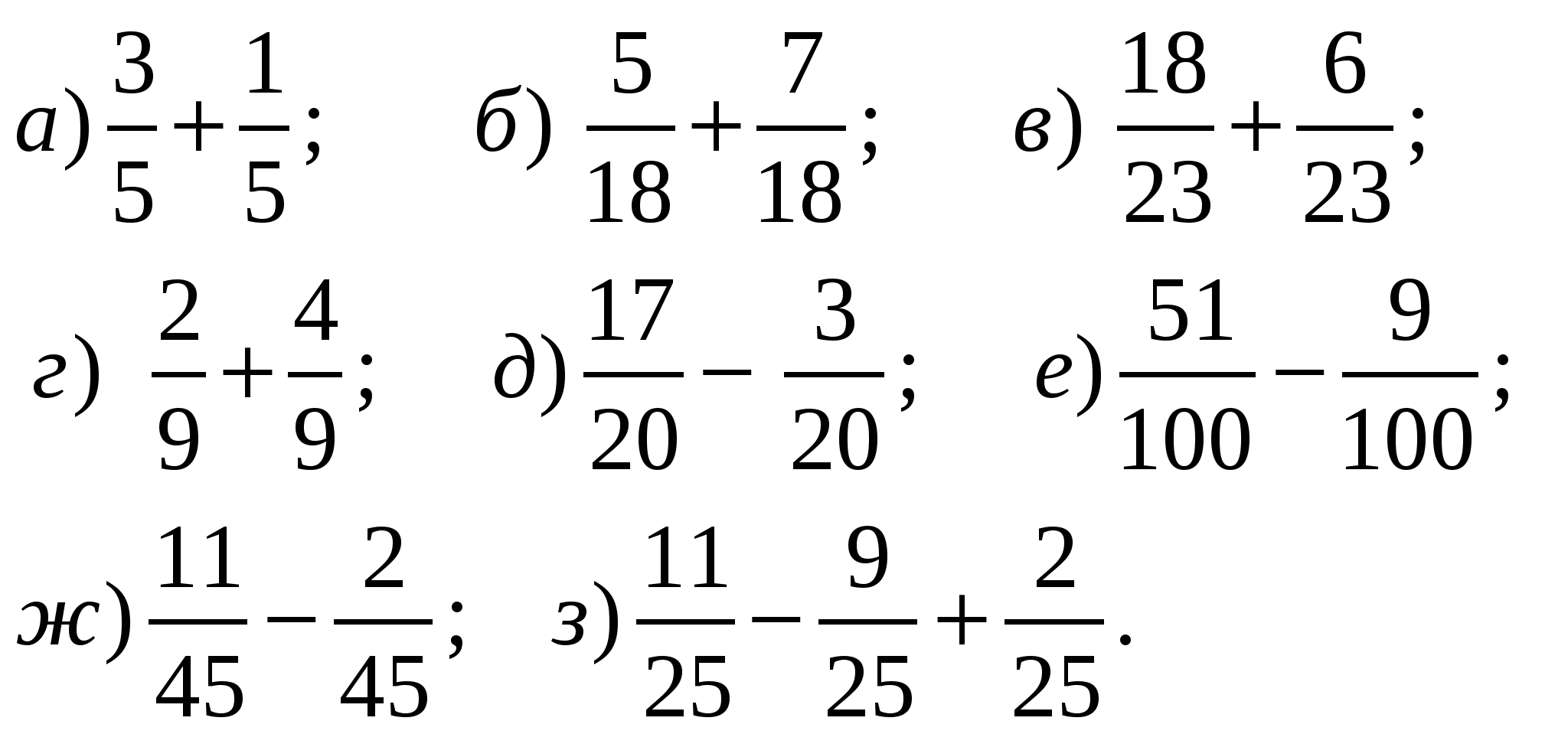
№5. Вычислите:










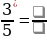
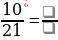
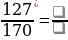
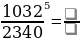
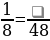
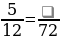
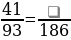
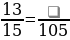
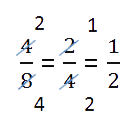

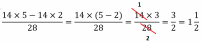
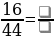
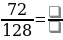
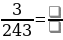
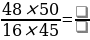


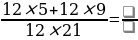
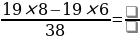

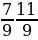
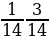
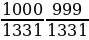
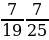
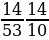
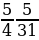
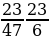
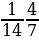
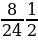

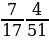

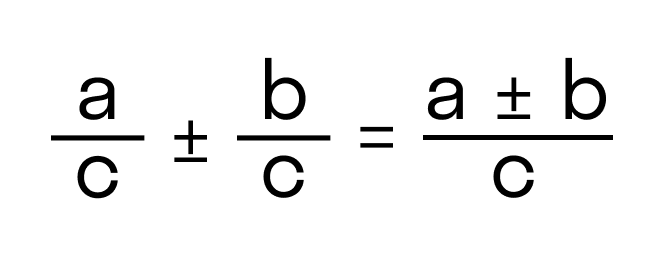 ри сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.
ри сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.
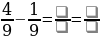
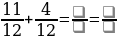
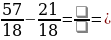
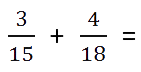
 айдем наименьшее общее кратное для определения единого делителя. Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.
айдем наименьшее общее кратное для определения единого делителя. Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.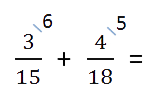 0 : 15 = 6,
0 : 15 = 6,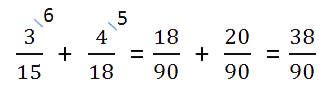
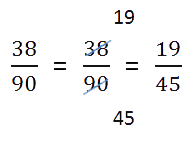
 Задание 6. Вычислите (если надо, сократите/выделите целую часть):
Задание 6. Вычислите (если надо, сократите/выделите целую часть):