Разработка по теме: "Основы логики"

Тема: «Основы алгебры логики»

Логика

• Это наука о законах и формах мышления.
• Она изучает абстрактное мышление как средство познания объективного мира.
• В логике основным объектом является высказывание

Логическое высказывание

Логическое высказывание — это любое повествовательное пpедлoжение, в oтнoшении кoтopoгo можно oднoзначнo сказать, истинно oнo или лoжнo.

Выражения:

• «Уходя, гасите свет и закрывайте дверь.»
• «Да здравствует мыло душистое и полотенце пушистое!»

не являются высказываниями, т. к. нельзя сказать, являются они истинными или ложными

В алгебре логики простым высказываниям ставятся в соответствие логические переменные, обозначаемые прописными буквами латинского алфавита. Например,

А — У кошки 4 ноги. А = 1 (ИСТИНА)

В — Томск — столица России. В = 0 (ЛОЖЬ)

С — Всякий квадрат есть параллелограмм. С= 1 (ИСТИНА)

D — Всякий параллелограмм есть квадрат. D = 0 (ЛОЖЬ)

Виды сложных высказываний

• Соединительные (связка И ).

« Саша играет на гитаре и на фортепиано », « Петров — врач и шахматист ».

• Разделительные (связка ИЛИ ).

« Вторым уроком будет физика или химия », « Мама купила торт или конфеты ».

• Условные (связка ЕСЛИ…, ТО ).

« Если придет друг, то мы посмотрим фильм »;

« Если будет ясная погода, то мы пойдем за грибами ».

• Эквивалентные (связка ТОГДА И ТОЛЬКО ТОГДА…, КОГДА ).

« Дождь идет тогда и только тогда, когда на небе есть тучи»;

«Саша и Ваня пойдут гулять тогда и только тогда, когда сделают уроки и выполнят обязанности по дому ».

• Высказывания с внешним отрицанием (связка НЕВЕРНО, ЧТО ).

« Неверно, что Таня и Света придут ко мне на день рождения »;

« Неверно, что все птицы летают ».

Основная задача математической логики — на основании ложности или истинности простых высказываний определить значение сложного высказывания.

Логические операции

И — логическое умножение или конъюнкция

• Обозначение операции в алгебре высказываний:

И ,  ,  , &.

• Обозначение в языках программирования: and .
• Если обозначить простые высказывания А = « Саша играет на гитаре »; В = « Саша играет на фортепиано », тогда сложное высказывание F = « Саша играет на гитаре и на фортепиано » можно записать как

F = А  В.

Таблица истинности операции И

Диаграмма Эйлера — Венна

В алгебре множеств конъюнкции соответствует операция пересечения множеств.

А

В

0

F = А  В

0

0

1

0

1

1

0

0

1

0

1

ИЛИ — логическое сложение или дизъюнкция

• Обозначение операции в алгебре высказываний:

ИЛИ,  , +.

• Обозначение в языках программирования: or .
• Обозначим сложное высказывание « Мама купила торт или конфеты » буквой F и запишем его на языке алгебры логики.

Пусть А — « Мама купила торт »; В — « Мама купила конфеты », тогда

F = А  В .

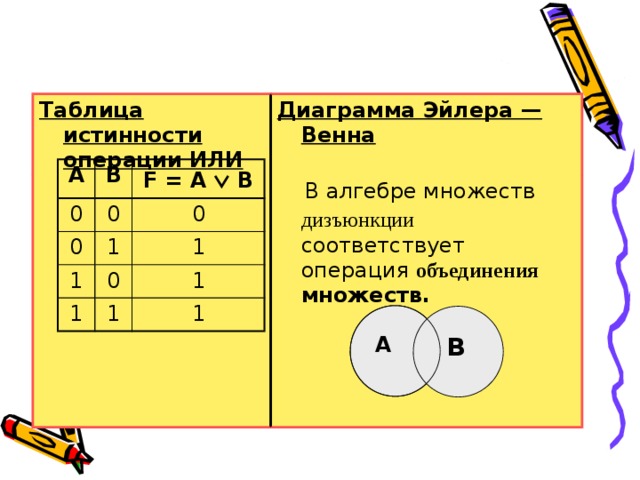
Таблица истинности операции ИЛИ

Диаграмма Эйлера — Венна

В алгебре множеств дизъюнкции соответствует операция объединения множеств.

А

В

0

F = А  В

0

0

1

0

1

1

1

0

1

1

1

А

В

НЕ — логическое отрицание или инверсия

• Обозначение отрицания в алгебре высказываний:

НЕ А,  А , ┐А.

• Обозначение в языках программирования: not .
• Пусть А = « Четыре — четное число » — истинное высказывание, тогда высказывание « Четыре — нечетное число » будет являться отрицанием высказывания А и будет ложно. На языке алгебры логики это будет выглядеть как

F =  А.

Таблица истинности операции НЕ

Диаграмма Эйлера-Венна

А

F =  А

0

1

1

0

А

 А

ЕСЛИ–ТО — логическое следование или импликация

• Обозначение импликации в алгебре высказываний: → .
• Пусть высказывание А = « Данный четырёхугольник — квадрат » и высказывание В = « Около данного четырёхугольника можно описать окружность ».
• Тогда составное высказывание

F = А → В

понимается как « Если данный четырёхугольник квадрат, то около него можно описать окружность ».

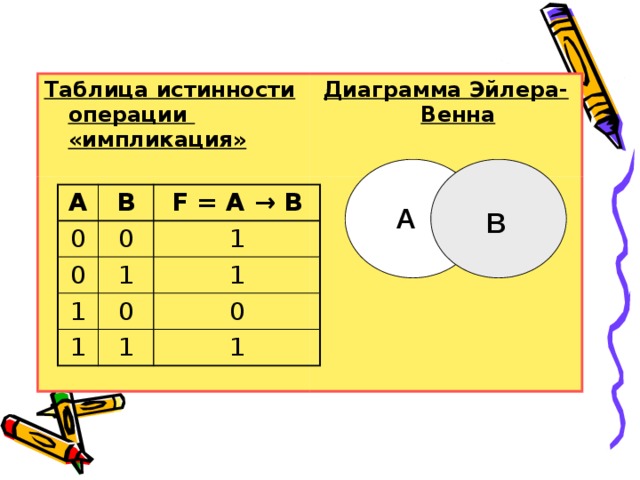
Таблица истинности операции «импликация»

Диаграмма Эйлера-Венна

А

В

0

F = А → В

0

0

1

1

1

0

1

1

1

0

1

А

В

РАВНОСИЛЬНО — логическое равенство или эквиваленция

• Эквиваленция (двойная импликация) — это логическая операция, выражаемая связками тогда и только тогда…, когда; необходимо и достаточно; равносильно; в том и только том случае.
• Обозначение эквиваленции в алгебре высказываний:

↔ , ~, ≡.

• Пусть высказывание А = « Идет дождь » и высказывание В = « На небе тучи ».

Тогда составное высказывание

F = А ↔ В

понимается как « Дождь идет тогда и только тогда, когда на небе есть тучи ».

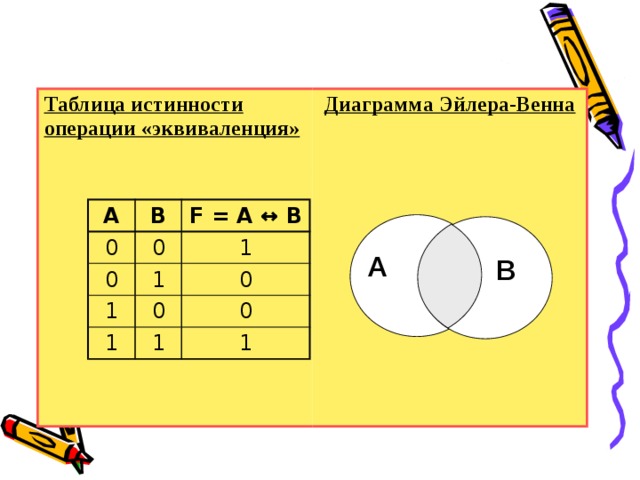
Таблица истинности операции «эквиваленция»

Диаграмма Эйлера-Венна

А

В

0

0

0

F = А ↔ В

1

1

1

1

0

0

1

0

1

А

В