Разработка презентации "Решение старинных русских задач"

РЕШЕНИЕ

СТАРИННЫХ

РУССКИХ ЗАДАЧ

Ре шение.

- кади кваса выпьет муж за один день.

- кади кваса выпьет муж за 10 дней.

- кади кваса выпьет жена за 10 дней.

• кади кваса выпивает жена за 1 день.

Значит, всю кадь она выпьет за 35 дней.

2. Из Москвы в Вологду.

Послан человек из Москвы на Вологду,

и велено ему в хождении своем совершати

на всякий день по 40 верст; потом другий

человек в другий (на следующий) день послан

в след его , и велено ему идти на день 45 верст,

и ведательно есть, в коликий день постигнет (догонит) второй первого.

Решение.

Если один человек каждый день идет по 40 верст,

а другой по 45 верст, то второй путник

каждый день будет приближаться

к первому на 5 вёрст (45 - 40 =5).

Значит, второй сократит расстояние в 40 вёрст

и догонит первого через 8 дней (40 : 5 =8).

3. Собака и заяц.

Собака усмотрела зайца в 150 саженях от себя.

Заяц пробегает за 2 минуты 500 саженей,

а собака - за 5 минут 1300 саженей.

За какое время собака догонит зайца?

Решение.

Если заяц пробегает 500 саженей за 2 минуты,

то за 1 минуту он пробежит 250 саженей.

Собака пробегает за 5 минут 1300 саженей,

тогда за 1 минуту она пробежит 260 саженей.

Расстояние между ними - 150 саженей,

а собака каждую минуту догоняет зайца на 10 сажень,

значит, она догонит его через 15 минут .

4.Ответ учителя.

Спросил некто учителя: «Скажи, сколько у тебя в классе учеников,

так как хочу отдать к тебе в учение своего сына».

Учитель ответил: «Если придет еще учеников столько же,

сколько имею, и полстолька, и четверть столько, и твой сын,

тогда будет у меня учеников 100».

Спрашивается, сколько было у учителя учеников?

Решение.

Пусть х – количество детей в классе.

По условию задачи составим и решим уравнение.

│ · 4

4 х + 4 х + 2 х + х + 4 = 400

(4 + 4 + 2 + 1 ) · х = 396

11 х = 396

х = 36

Значит, у учителя было 36 учеников.

5 . Кому пасти овец?

У пятерых крестьян – Ивана, Петра, Якова, Михаила и Герасима – было 10 овец.

Не могли они найти пастуха, чтобы пасти овец, и говорит Иван остальным:

«Будем братцы, пасти овец по очереди – по столько дней, сколько каждый из нас имеет овец».

По сколько дней должен каждый крестьянин пасти овец, если известно, что

у Ивана в два раза меньше овец, чем у Петра,

у Якова в два раза меньше, чем у Ивана;

Михаил имеет овец в два раза больше, чем Яков,

а Герасим – вчетверо меньше, чем Пётр?

Решение.

_______________________

Я = Г И = М П

Пусть х овец имеет Яков,

тогда 2х овец - у Ивана, у Петра - 4х овец,

у Герасима - х овец, а Михаил имеет 2х овец.

По условию задачи составим и решим уравнение.

х + 2х + 4х + х + 2х = 10

(1 + 2 + 4 + 1 + 2)х = 10

10х = 10

х = 1

Значит, у Якова и Герасима - по 1 овце,

у Ивана и Михаила - по 2 овцы,

а у Петра - 4 овцы.

6. Покупка масла.

Некий человек покупал масло. Когда он давал деньги за 8 бочек масла, то у него оставалось 20 алтын. Когда же стал давать за 9 бочек, то не хватило денег полтора рубля с гривною.

Сколько денег было у этого человека?

Решение.

20 алт. = 6 грив. 1,5 руб. = 150 к. = 15 грив.

Пусть х гривен – стоимость одной бочки масла.

По условию задачи составим и решим уравнение.

8х + 6 = 9х – (15 + 1)

9х – 8х = 6 + 16

х = 22

22 гривны стоит одна бочка масла.

8 · 22 + 6 = 176 + 6 = 182 (грив.)

182 грив. = 18 руб.2 грив.

Значит, у человека было 18 рублей и 2 гривны.

7 . Покупка коровы.

Два человека хотят купить корову. Говорит первый второму:

«Если ты дашь мне твоих денег, то я один смогу заплатить её цену».

А второй отвечает первому: «Дай мне твоих денег,

тогда и я заплачу её цену».

Сколько у каждого из них денег, если корова стоит 24 рубля?

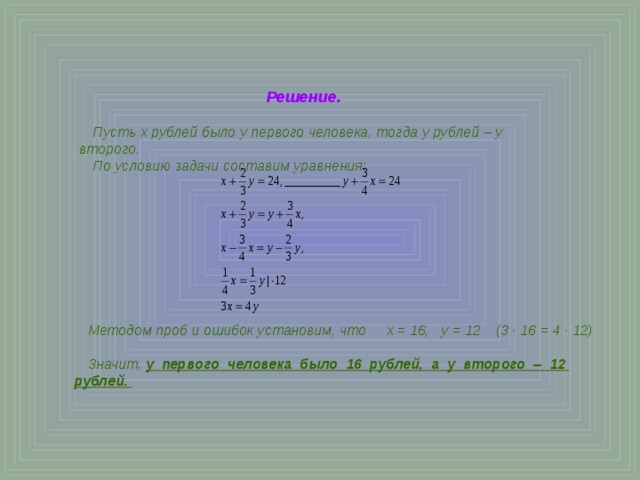
Решение.

Пусть х рублей было у первого человека, тогда у рублей – у второго.

По условию задачи составим уравнения:

Методом проб и ошибок установим, что х = 16, у = 12 (3 · 16 = 4 · 12)

Значит, у первого человека было 16 рублей, а у второго – 12 рублей.

СПАСИБО

ЗА

ВНИМАНИЕ !