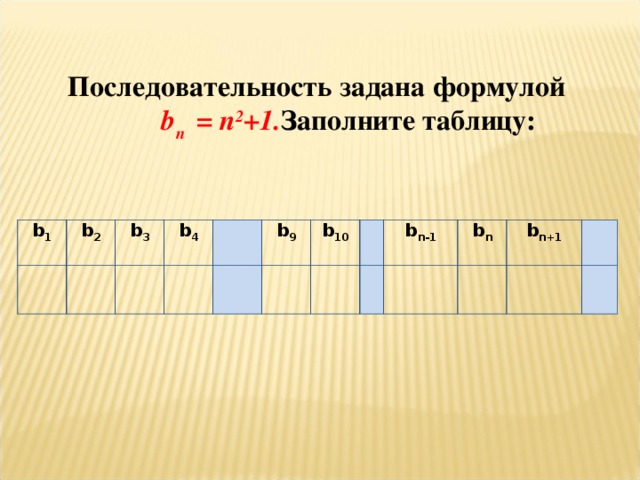
| 3. Изучение нового материала | - Посмотрев видеоролик, что нового вы для себя открыли? - С какой последовательностью чисел вы познакомились? - Можно сделать вывод, что в нашей жизни много что возникло не случайно, все продумано и подчинено единым законам. - Итак, как вы думаете, какая тема урока? - Открываем тетради, записываем число и тему урока. - Давайте запишем в тетради последовательность Фибоначчи. - В данной последовательности каждый член равен сумме двух предыдущих.
- Теперь вы приведите примеры каких-либо числовых последователь-ностей.
- На какие группы можно разделить приведенные последователь-ности? - Записываем в тетради классификацию последователь-ностей.
- Итак, давайте обсудим, к каким видам последователь-ностей относятся те последователь ности, которые мы только что рассмотрели? -Теперь возникает вопрос, как обозначать последовательность и ее элементы используя математический язык?
- Если есть у нас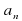 , следующий элемент , следующий элемент  , тогда какой будет предыдущий? , тогда какой будет предыдущий? - Если дан  , то каким будет следующий и предыдущий элементы последователь-ности? , то каким будет следующий и предыдущий элементы последователь-ности? - Давайте выясним какими способами можно задавать последователь-ности? - Итак, мы узнали что такое числовая последователь-ность, ее обозначение, виды, способы задания. |
[Числовые последовательности] [Учащиеся записывают число, классная работа, тему урока в тетрадях] [1) 1, 1, 2, 3, 5, 8, 13, … - последовательность Фибоначчи;
2)1,2,3,4,5,6,7,8,9,10,… - последовательность натуральных чисел; 3) 2,4,6,8,10,12,14,16, … - последовательность четных чисел; 4) 1,2,3,4,5,6,7,8,9. – последовательность однозначных натуральных чисел; 5) 10,20,30,40,50,60,70,80,90. – последовательность двузначных чисел, кратных 10. 6) -5,-10,-15,-20,-25,… - последовательность отрицательных чисел, кратных 5; 7) 0,1,0,1,0,1,0, … - последовательность чисел, на четных местах 1, на нечетных 0; 8) 10,7,4,1,-2,-5,-8, …-последовательность чисел каждый член, которой меньше предыдущего на 3.]
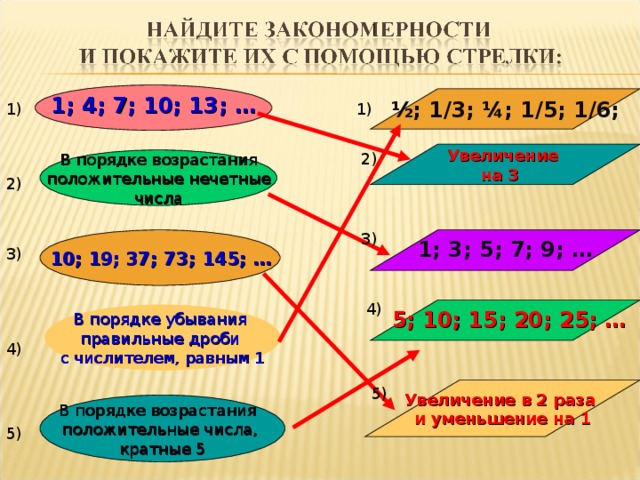
[Классификация последователь-ностей: 1) Бесконечные и конечные. 2) Возрастающие и убывающие.] [Устно соотносят последовательности]
[ , , , ,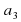 , , , , ,..., ,...,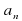 , … - члены последовательности. , … - члены последовательности. Последовательность  , , , ,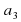 , , , , ,..., ,...,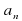 , … обозначают – ( , … обозначают – (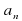 ). ). n – порядковый номер (место) члена последовательности.  - предыдущий член последовательности, - предыдущий член последовательности,
 - последующий член последовательности.] - последующий член последовательности.]
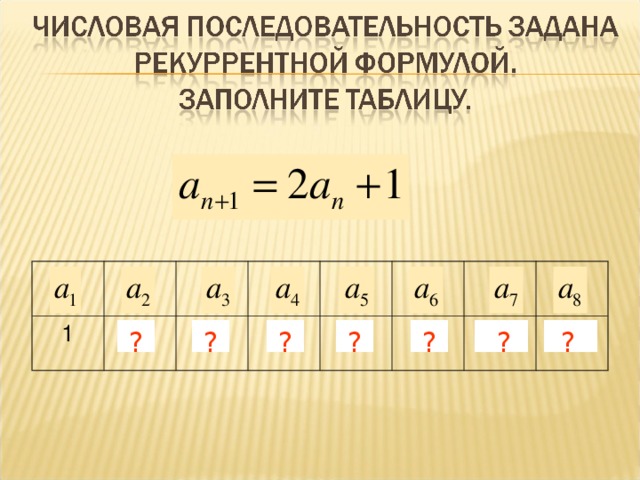
[Заполнение карточек] |
[Последовательность Фибоначчи]
[Числовые последовательности]
[1) 1, 1, 2, 3, 5, 8, 13,, … - последовательность Фибоначчи
2) 1,2,3,4,5,6,7,8,9,10,… - последовательность натуральных чисел; 3) 2,4,6,8,10,12,14,16, … - последовательность четных чисел; 4) 1,2,3,4,5,6,7,8,9. – последовательность однозначных натуральных чисел; 5) 10,20,30,40,50,60,70,80,90. – последовательность двузначных чисел, кратных 10. 6) -5,-10,-15,-20,-25,… - последовательность отрицательных чисел, кратных 5; 7) 0,1,0,1,0,1,0, … - последовательность чисел, на четных местах 1, на нечетных 0; 8) 10,7,4,1,-2,-5,-8, …-последовательность чисел каждый член, которой меньше предыдущего на 3.]
[Классификация последовательностей: 1) Бесконечные и конечные. 2) Возрастающие и убывающие.]
[Обозначают члены последовательности:  , , , ,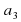 , , , , ,..., ,...,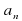 , … , …
Последовательность  , , , ,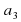 , , , , ,..., ,...,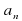 , … обозначают – ( , … обозначают – (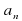 ). ). n – порядковый номер (место) члена последовательности.  - предыдущий член последовательности, - предыдущий член последовательности,
 - последующий член последовательности.] - последующий член последовательности.]
[ , , , ,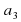 ,…, ,…, , , ,…, ,…, , ,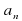 , , , ,  ,…] ,…]
[ , ,  ] ]
[Раздается раздаточный материал, Приложение1] |







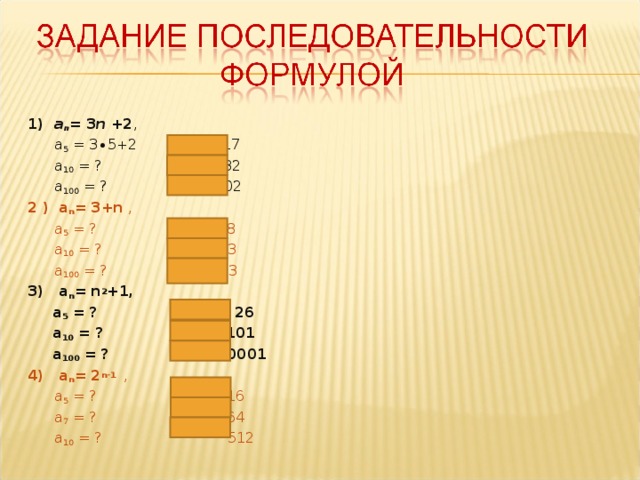
 = 3
= 3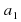 =
=  =
=  =
=  =
=  =
=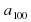 =
= 
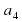 =
=  =
= =
= 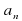 , следующий элемент
, следующий элемент  , тогда какой будет предыдущий?
, тогда какой будет предыдущий? , то каким будет следующий и предыдущий элементы последователь-ности?
, то каким будет следующий и предыдущий элементы последователь-ности? ,
, ,
,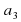 ,
, ,
, ,...,
,..., - предыдущий член последовательности,
- предыдущий член последовательности, ,
, ,…,
,…, ,…]
,…] ,
,  ]
] =
=  =
= = 3
= 3 =
=  =
=  = 2,
= 2, 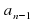


 =
=