У р о к п о в т о р е н и я № 6.
Решение задач на встречное движение
Основная дидактическая цель урока: учить решать задачи на встречное движение; повторить взаимосвязь между величинами «скорость», «время», «расстояние»; совершенствовать вычислительные навыки учащихся.
Х о д у р о к а
I. Организационный момент
II. Устный счёт
1. С. 165, № П.49.
(26,25; 13.2; 0,5; 12,5; 502.)
2. Решите задачу.
1) Самокат проехал 24 км со скоростью 12 км/ч. Сколько времени он потратил на дорогу? (2 ч.)
2) Муха летела 20 с со скоростью 6 м/с. Какое расстояние она пролетела? (120 м.)
3) За 6 ч туристы проплыли на лодке 60 км. С какой скоростью они плыли? (10 км/ч.)
III. Работа по теме урока
Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Например, если из двух пунктов на встречу друг другу отправятся два пешехода, причём скорость первого будет 100 м/мин, а второго 105 м/мин, то скорость сближения будет составлять 205 м/мин: v = v1 + v2 = 100 + 105 = 205 м/мин.
– Рассмотрим пример.
1. С. 165, № П.52.
– О каком движении идёт речь в этой задаче?
– Что мы можем найти, зная расстояние и время, через которое произошла встреча?
– Что следует обозначить через х?
Пусть скорость товарного поезда будет х км/ч.
Тогда скорость пассажирского будет 1,5х км/ч.
Найдём скорость сближения:
x + 1,5x (км/ч).
Найдём скорость сближения иначе:
312,5 : 2,5 (км/ч).
Оба выражения обозначают одно и то же.
Значит, можем составить уравнение:
x + 1,5x = 312,5 : 2,5
2,5x = 125
x = 125 : 2,5
x = 50 (км/ч) – скорость товарного поезда.
1,5x = 1,5 ・ 50 = 75 (км/ч) – скорость пассажирского поезда.
– К этой задаче можно составить и другое уравнение. Подумайте, какое.
2,5(1,5х + х) = 312,5
6,25 х = 312,5
х = 50 (км/ч) – скорость товарного поезда.
1,5х = 1,5 ・ 50 = 75 (км/ч) – скорость пассажирского поезда.
2. С. 165, № П.54 (работа в паре).
Пусть скорость первого всадника будет х км/ч.
Тогда скорость второго всадника будет х + 3,2 (км/ч).
Скорость сближения равна:
х + х + 3,2 (км/ч) или 36 : 1,2 = 30 (км/ч).
По условию расстояние равно 40 км.
За 1,2 ч всадники преодолели 40 – 4 = 36 км.
Значит, можем составить уравнение:
(х + х + 3,2) = 30
2х = 30 – 3,2
2х = 26,8
2х = 26,8 : 2
х = 13,4 (км/ч) – скорость первого всадника.
х + 3,2 = 13,4 + 3,2 = 16,6 (км/ч) – скорость второго всадника.
Ответ: 13,4 км/ч и 16,6 км/ч.
IV. Работа по учебнику
С. 161, № П.2 (устно).
(Если это задание вызовет затруднение, можно предложить выполнить его на конкретном примере.
Ответ: число уменьшится на 54.)
– Изменится ли ответ, если число будет не девятизначное, а семи-, шести-, пятизначное?
V. Работа над комбинаторной задачей
– Сколько различных шестизначных чисел можно составить с помощью цифр 1, 2, 3; 4; 5; 6, если цифры в записи числа не могут повторяться?
– Какие числа надо составить?
– Сколько цифр можем использовать?
– Какое стоит условие?
– Сколькими способами мы можем выбрать цифру на первое место? (6.)
– Сколькими способами можно выбрать вторую, третью, четвёртую, пятую и шестую?
– Как решить эту задачу? (6! = 720 способов.)
VI. Самостоятельная работа
В а р и а н т 1
1. Два пешехода вышли одновременно навстречу друг другу из двух разных пунктов, расстояние между которыми 36 км. Скорость первого 6 км/ч. С какой скоростью шёл второй пешеход, если они встретились через 3 ч? (6 км/ч.)
2. Из двух гнёзд одновременно навстречу друг другу вылетели два орла. Встретились они через 6 с. Скорость одного орла 6 м/с, а скорость другого 16 м/с. Какое расстояние между гнёздами орлов? (132 м.)
В а р и а н т 2
1. От двух пристаней одновременно навстречу друг другу отошли две яхты. Скорость первой яхты 18 км/ч, скорость другой 15 км/ч. Через сколько часов яхты встретятся, если расстояние между пристанями 132 км? (4 ч.)
2. Два гребца поплыли одновременно навстречу друг другу с разных концов бассейна, длина которого 100 м. Первый плыл со скоростью 20 м/мин. С какой скоростью плыл второй гребец, если они встретились через 2 мин? (30 м/мин.)
VII. Рефлексия
– Фигура состоит из 12 равных квадратов. Разделите эту фигуру на четыре равные части.
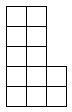
– Сегодня мы решали задачи, которые включают три величины. Какие?
– Как найти скорость по расстоянию и времени?
– Что надо знать, чтобы найти время?
Домашнее задание
С. 168, № П.94, № П.98.


















