Разработка урока в 10 классе "Решение графических задач на газовые законы"

Урок Решение графических задач «Газовые законы» 10 класс

Тип урока: Урок-практикум.

Цель урока: Привить умение применять законы изопроцессов, закон Менделлева-Клапейрона, уравнение состояния идеального газа, первый закон термодинамики при решении комбинированных графических задач

Задачи урока:

Образовательные: повторить виды изопроцессов, законы изопроцессов, закон Менделлева-Клапейрона, уравнение состояния идеального газа, первый закон термодинамики, привить умение применять законы к чтению графиков изопроцессов

Развивающие: развивать внимание и речь, совершенствовать навыки самостоятельной работы.

Воспитательные формировать целостное представление обучающихся о мире (природе, обществе и самом себе), о роли и месте физики в системе наук.

Оборудование:  компьютер учителя, мультимедийный проектор,

….. мы вспомним виды изопроцессов, законы изопроцессов, закон Менделлева-Клапейрона, уравнение состояния идеального газа и научимся применять эти законы при решении задач

Фронтальный опрос:

-Что называют изопроцессом?

-Какие изопроцессы различают?

-Опишите кратко каждый изопроцесс

-Покажите, какой вид имеет изотерма в координатах PV

- Покажите, какой вид имеет изотерма в координатах VT

- Покажите, какой вид имеет изобара в координатах VT

- Покажите, какой вид имеет изобара в координатах PT

- Покажите, какой вид имеет изохора в координатах PT

- Покажите, какой вид имеет изохора в координатах PV

- Запишите уравнение состояния идеального газа

-Запишите закон Менделлева-Клапейрона

-Запишите первый закон термодинамики

4. Решение задач

Задача 1. Постоянное количество одноатомного идеального газа участвует в процессе, график которого изображён на рисунке в координатах р-n, где р — давление газа, n — его концентрация. Определите, получает газ теплоту или отдаёт в процессах 1-2 и 2-3. Ответ поясните, опираясь на законы молекулярной физики и термодинамики.

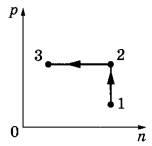
Решение.

1. По первому закону термодинамики количество теплоты, которое газ получает, равно сумме изменения его внутренней энергии ∆U и работы газа A: Q = ∆U + A. Концентрация газа n = N/V, где N — число молекул газа, V — его объём. Для идеального одноатомного газа внутренняя энергия   (где v — количество моль газа). По условию задачи N = const.

2. Так как на участке 1-2 концентрация газа не изменяется, его объём постоянен (изохорный процесс), значит, работа газа А=0. В этом процессе давление газа растёт, согласно закону Шарля температура газа также растёт, т.е. его внутренняя энергия увеличивается: ∆U 0. Значит, Q 0, и газ получает тепло.

3. На участке 2-3 концентрация газа уменьшается, значит, его объём увеличивается и работа газа положительна: А 0. Давление газа постоянно (изобарный процесс), по закону Гей-Люссака температура газа также увеличивается. Поэтому ∆U 0. По первому закону термодинамики Q 0. В этом процессе газ получает тепло.

Задача 2.На графике представлена зависимость давления неизменной массы идеального газа от его плотности. Опишите, как изменяются в зависимости от плотности температура и объём газа в процессах 1-2 и 2-3.

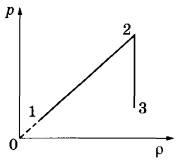
1. Плотность газа  , где m — масса газа, V — его объём. В соответствии

с уравнением Менделеева-Клапейрона  . На участке 1-2 давление изменяется пропорционально плотности газа:  . Следовательно, в этом процессе температура газа не изменяется. Поскольку плотность газа на этом участке возрастает, объём газа уменьшается.

2. В процессе 23 плотность газа постоянна, следовательно, объём газа не меняется. Давление газа при этом уменьшается, следовательно, согласно уравнению Менделеева-Клапейрона температура газа также уменьшается.

Задача 3. С идеальным газом происходит циклический процесс, pT-диаграмма которого представлена на рисунке. Наименьший объём, который занимает газ в этом процессе, составляет 60 л. Определите количество вещества этого газа. Ответ округлите до целых.

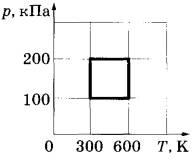
Решение.

Наименьший объем будет соответствовать наибольшему давлению при наименьшей температуре, то есть при p=200 кПа и T=300 К. Найдем количество вещества газа из уравнения Менделеева-Клапейрона:

,

откуда

.

Подставляя   м3, R=8,31 и   Па, получаем:

 моль.

Задача 4. На VT-диаграмме показано, как изменялись объём и температура некоторого постоянного количества разреженного газа при его переходе из начального состояния 1 в состояние 4. Как изменялось давление газа р на каждом из трёх участков 1-2, 2-3, 3-4: увеличивалось, уменьшалось или же оставалось неизменным? Ответ поясните, указав, какие физические явления и закономерности Вы использовали для объяснения.

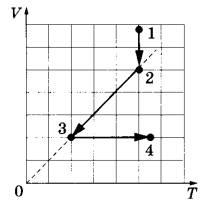
Решение.

1. Давление газа на участке 1-2 увеличивалось, на участке 2-3 не изменялось, на участке 3-4 увеличивалось.

2. На участке 1-2 процесс изотермический. По закону Бойля-Мариотта (pV = const) при уменьшении объёма давление увеличивается. На участке 2-3 процесс изобарный; значит, давление остаётся неизменным. На участке 3-4 процесс изохорный. По закону Шарля p/T = const при увеличении температуры давление увеличивается.

5. Д.З + рефлексия

задача (на следующем уроке решение разбирается)

Задача. В сосуде объёмом 10 л находится гелий. На рисунке показан график изменения давления гелия при изохорном нагревании. Сколько молей газа находится в сосуде? Ответ округлите до десятых.

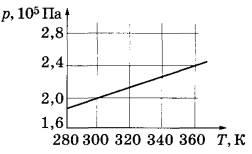
Решение.

Изохорный процесс – это термодинамический процесс при постоянном объеме. Так как объем не меняется, то число молей v в газе можно найти из уравнения Менеделеева-Клапейрона

,

откуда

.

Из графика видно, что при T=300 К давление равно   Па. Подставляя эти значения в формулу (при   м3), получаем:

 моль.