МОБУ СОШ д.Верхнекарышево
Разработка урока в 9 классе на тему:
Учитель математики: Муниров Ф.Х.
2022 год
Тема урока. График уравнения с двумя переменными.
Цель урока: добиться усвоения учащимися определения и алгоритма построения графика уравнения с двумя переменными. Сформировать умения формулировать изученное определение и объяснять алгоритм; применять их для решения задач на построение графиков уравнений с двумя переменными.
Тип урока: обобщения и систематизации знаний, формирования умений.
Наглядность и оборудование:опорный конспект.
Ход урока
IОрганизационный этап
Учитель рассказывает о приблизительном содержании учебного материала данного раздела.
IIПроверка домашнего задания
Учитель проверяет выполненный учащимися анализ тематической контрольной работы № 3.
IIIФормулирование цели и задач урока.
Мотивация учебной деятельности учащихся
На этом этапе урока целесообразными будут слова учителя о том, что материал предыдущего раздела «Функция, свойства функции» может быть использован не только для решения квадратных неравенств и задач, предусматривающих их решение, но и для решения других задач. В частности, если вспомнить материал, изученный учащимися на уроках геометрии (уравнение фигуры в декартовых координатах), то становится понятным, что функции и их графики — одно из средств нахождения множеств точек, координаты которых удовлетворяют определенному уравнению с двумя переменными. Такую задачу учащиеся уже решали на уроках алгебры в 7 классе (во время изучения темы «График линейного уравнения с двумя переменными»). Итак, на данном уроке стоит вопрос о систематизации знаний учащихся о графике уравненияс двумя переменными, формировании умений выполнять его построение и решать простейшие задачи па его применение.
IV. Актуализация опорных знаний и умений учащихся
Устные упражнения
Даны выражения:
1)x2+y;2)xy+3;3)у(х+2).
Найдите значение каждого из данных выражений:
а) при х = -1, у = 2;б) при х = -0,5, у = 0,4;в) при 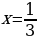 ,у = 3.
,у = 3.
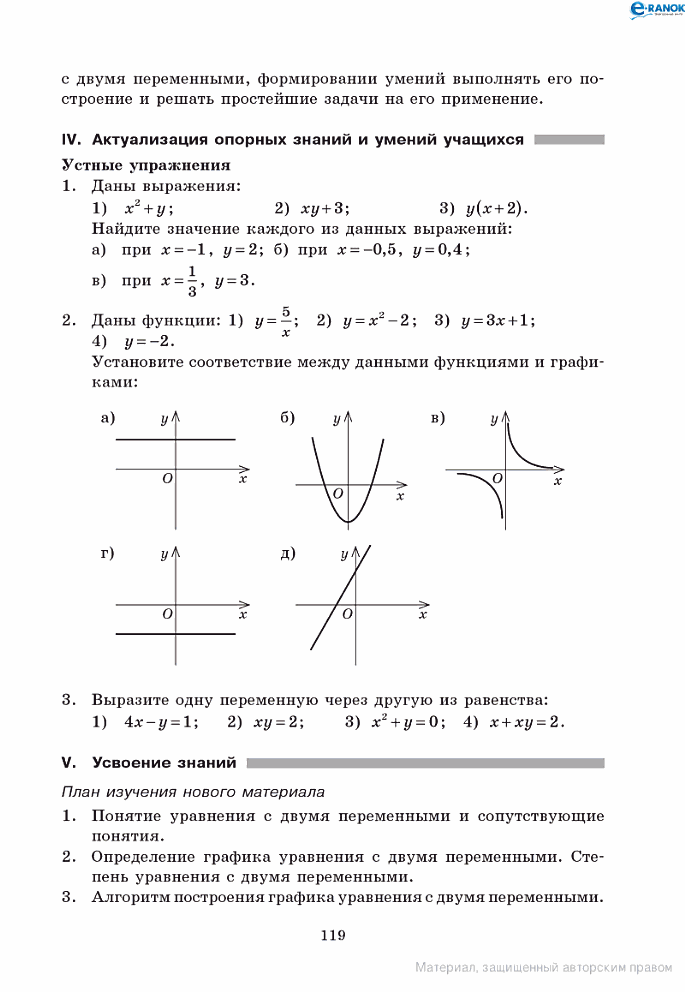
Даны функции: 1) у=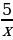 ; 2) у = х2-2;3) у=3x + 1;4) у = -2.
; 2) у = х2-2;3) у=3x + 1;4) у = -2.
Установите соответствие между данными функциями и графиками:
3. Выразите одну переменную через другую из равенства:
1) 4х-у = 1; 2) ху = 2; 3) х2 + у = 0; 4) х + ху = 2.
V. Усвоение знаний
План изучения нового материала
Понятие уравнения с двумя переменными и сопутствующие понятия.
Определение графика уравнения с двумя переменными. Степень уравнения с двумя переменными.
Алгоритм построения графика уравнения с двумя переменными.
Опорный конспект
Уравнение с двумя переменными
Примеры: х2 + у2 = 25,ху = 4, х + ху = 1.
Сопутствующие понятия
Решение уравнения с двумя переменнымихиу — это упорядоченная пара (х; у), преобразующая уравнение в верноеравенство.
Например, пара (2;3) является решением уравненияху=6 ,
так как прих = 2 и y = 3 данное уравнение имеет вид 2*3 = 6,
т. е. образуется верное равенство.
Степень целого уравнения с двумя переменными p(x;y) = 0определяется как степень многочленаР(х; у), если он приведен к стандартному виду.
Например, х2 + ху + у = 0— уравнение второй степени.
График уравнения с двумя переменными хиу — это множество точек координатной плоскости с координатами (х;у), где пара (х;у) является решением данного уравнения с двумяпеременными.
Алгоритм построения графика уравнения с двумяпеременными
Если уравнение можно привести к виду (х-а)2 +(у-b)г = R2где a, b— произвольные числа, aR0, то графиком этогоуравнения будет окружность радиуса Rс центром (а; b).В других случаях (если нет модуля) выражаем у через хи строим график полученной функцииy = f(x).
Пример.Построим график уравнения:
1) 2x-3у = 6;2) х2 + у2 = 9;3)ху = 4.
Решение (см. рисунок)
1) 2х-3у = 6у=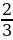 x - 2— линейная функция.
x - 2— линейная функция.
2) х2 + у2 = 9 = З2 — уравнение окружности радиуса 3 с центром (0;0).
3) ху = 4; у = 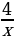 — обратная пропорциональность.
— обратная пропорциональность.
| x | -4 | -2 | -1 | 1 | 2 | 4 |
| y | -1 | -2 | -4 | 4 | 2 | 1 |

Методический комментарий
Основная часть учебного материала урока — это знания и умения, полученные учащимися при изучении алгебры в предыдущих классах. На данном уроке осуществляется преимущественноповторение, обобщение и систематизация учебного материала.
Формирование умений
Устные упражнения
Является ли решением уравнения х2 + у = 10
пара чисел: 1)x= 3, у = 1; 2) (-2;6)?
2. Принадлежат ли точки А(-2;3); В(0;0); С(3;0) графику уравнения:
1)ху = -6;2) х2 -у = 9;3) х2 + у2 = 9?
3. Определите степень уравнения:
1) ху-2у = 5;2) х2-у = 2;3) х2 + 3у2 = 0.
4. Что является графиком уравнения:
1) х2 + у2 = 4;2) (х-1)2 + (у + З)2 = 9;
3) х =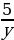 ;4) х = Зу-1?
;4) х = Зу-1?
Письменные упражнения
Для реализации дидактической цели урока следует решить задачи такого содержания:
определить, является ли данная пара чисел решением уравнения с двумя переменными;
построить график уравнения с двумя переменными;
найти несколько решений уравнения с двумя переменными аналитически и графически;
на повторение: решить системы линейных уравнений с двумя переменными.
Методический комментарий
Для лучшего усвоения учащимися содержания материала урока рекомендуется при выполнении соответствующих задач неоднократно повторять определения решения уравнения с двумя переменными, графика уравнения с двумя переменными и алгоритм его построения (см. опорный конспект).
Итоги урока
Контрольные вопросы
1. Приведите примеры уравнений с двумя переменными разных видов.
2. Что называется решением уравнения с двумя переменными? Для каждого из приведенных в п. 1 уравнений найдите хотя бы одно решение (если оно есть).
3. Приведите примеры уравнений с двумя переменными, графиками которых являются:
1) окружность; 2) прямая;
3) гипербола; 4) парабола.
4. Каким общим свойством обладает любая точка графика данного уравнения с двумя переменными?
VIII. Домашнее задание
Выучить определение понятий, рассмотренных на уроке.
Решить № 402
Повторить способы решения систем линейных уравнений с двумя переменными (по справочнику для 7 класса);






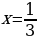 ,у = 3.
,у = 3.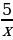 ; 2) у = х2-2;3) у=3x + 1;4) у = -2.
; 2) у = х2-2;3) у=3x + 1;4) у = -2.
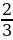 x - 2— линейная функция.
x - 2— линейная функция.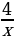 — обратная пропорциональность.
— обратная пропорциональность.
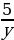 ;4) х = Зу-1?
;4) х = Зу-1?









