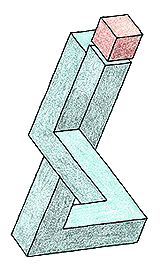Развитие пространственного представления учащихся на уроках стереометрии

Развитие пространственного представления учащихся

на уроках стереометрии

Если ученик в школе не научится

сам ничего творить, то в жизни он всегда будет только подражать,

копировать, т.к. мало таких, которые бы,

научившись копировать, умели сделать самостоятельное приложение этих сведений.

Одной из главных целей преподавания геометрии как составной части математического образования принято считать формирование у школьников пространственных представлений. И это не столько внутренняя задача курса геометрии, сколько внешняя, связанная с подготовкой школьников к жизни, к труду в различных сферах деятельности. Ориентация человека в пространстве является тем фундаментом, который необходим для практической деятельности по таким специальностям как, например, архитектор, инженер, строитель, геодезист, чертежник, оператор, диспетчер, космонавт и т.п.

Способность создавать и оперировать пространственными образами характеризует уровень общего интеллектуального развития человека. В психологических исследованиях экспериментально подтверждено, что между склонностью учащихся к соответствующим профессиям и уровнем развития у них пространственных представлений имеет место статистически достоверная связь.

Как внутренняя задача пространственные представления необходимы учащимся для восприятия учебного материала курса геометрии и для решения различного рода практических и теоретических задач.

Но, несмотря на столь важную роль, которую играют пространственные представления, они сформированы у учащихся школ на достаточно низком уровне. Об этом свидетельствуют и факты из опыта работы, и анализ изученной по этому вопросу литературы. Заметим, что учащиеся испытывают бо́льшие трудности в оперировании образами, нежели в их создании.

Вот почему учитель должен обратить самое пристальное внимание на формирование у школьников умения оперировать образами, оптимизировать и повысить эффективность работы на уроках геометрии для решения данной проблемы.

Ниже представлен собственный опыт и некоторые этапы работы над развитием пространственного представления обучающихся:

1. Выявление уровня подготовленности ребят к восприятию школьного курса стереометрии.

Выявить уровень подготовленности ребят к восприятию школьного курса стереометрии учителю могут помочь тесты, которые можно найти в методической литературе, например:

ТЕСТ № 1

ПРОСТРАНСТВЕННОЕ МЫШЛЕНИЕ (стандартное восприятие)

1. Внимательно прочитайте инструкцию. Время на работу с тестом ровно 20 минут, поэтому НЕ ОТКРЫВАЙТЕ ЗАДАНИЕ до тех пор, пока учитель не даст сигнал приступать к работе.

2. Вам будут предложены 30 рисунков, на которых изображены 15 кубов (каждый из них разрезан на две части), причём все «первые половинки» обозначены числами 1-15, а все «вторые половинки» обозначены (в другом порядке) буквами а – п.

Найдя пару для половинок 1 – 15, вы должны записать их буквами в таблице результатов под соответствующим номером.

По сигналу учителя переверните страницу и приступайте к работе.

Желаем удачи!

1. Работа с чертежом.

Важнейшим средством формирования у школьников пространственных представлений является чертёж.

При решении стереометрических задач требования к качеству чертежа, его наглядности возрастают по сравнению с задачами планиметрическими.

Первый и важнейший этап решения геометрической задачи всегда начинается с построения чертежа. Нельзя научиться решать достаточно содержательные геометрические задачи без прочных навыков по изготовлению "хороших" чертежей. Нужна привычка - не начинать решать задачи, пока не сделан "большой и красивый" чертеж, удовлетворяющий и математическим требованиям, и эстетическим критериям. И ещё - желательно научиться делать чертежи достаточно хорошего качества от руки, поскольку установка на использование чертёжных инструментов может сузить оперативный простор в процессе работы над решением.

Обучению учащихся умению изображать объемную фигуру плоскостным чертежом должно быть уделено самое пристальное внимание. Учащиеся должны знать, что для изображения объемной фигуры достаточно научиться изображать её отдельные точки, определяющие положение этой фигуры в пространстве. Полезно сообщить требования к оформлению чертежа и свойства, которые необходимо учитывать при выполнении проекционных чертежей и различных построений.

Необходимо научить учащихся относиться к чертежу критически, чему способствует учебное правило: "Не разрешается использовать в рассуждениях свойства фигуры, видимые на чертеже, если мы не можем обосновать их, опираясь на аксиомы и теоремы, доказанные ранее".

Школьники привыкают работать с шаблонными изображениями геометрических фигур, а поэтому они часто оказываются беспомощными, когда им надо создать образ по чертежу, на котором пространственный объект расположен нетрадиционно. Поэтому целесообразно рассматривать различные изображения одного и того же тела. Например, различные изображения куба:

Формированию у ребят умений изображать плоскостным чертежом пространственные геометрические тела будут способствовать, например, такие задачи:

1. Анализируя изображение геометрической фигуры, ответьте на вопросы:

а) Какие фигуры изображены на рисунках?

б) Назовите видимые элементы фигур.

в) Какие плоские геометрические фигуры могут составлять поверхности изображенных фигур?

2. Постройте изображение фигуры до:

а) куба

б) треугольной пирамиды

г) произвольного многоугольника

Итак, общие требования к чертежу можно выразить двумя словами: он должен быть верным и наглядным.

3. Тренировочные упражнения на развитие пространственного представления. Например,

4.Решение задач исследовательского характера.

1)Построить сечение куба по трём заданным точкам

2) Даны две параллельные прямые a и b. Как может быть расположена по отношению к ним третья прямая с? Сделайте соответствующие рисунки.

1. Задачи на привитие интереса к изучению стереометрии.

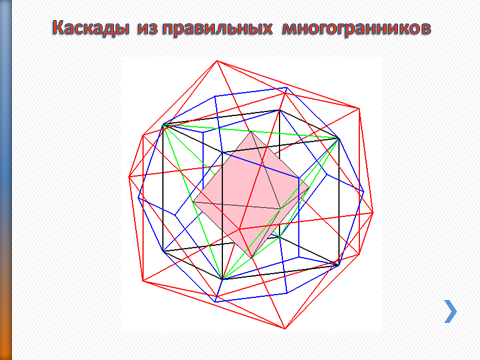
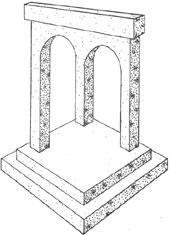
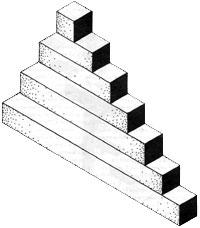
Для привития интереса к изучению стереометрии, в рамках эстетического воспитания и расширения математического кругозора использую в рамках урока работу с «невозможными объектами».

"Невозможные объекты" построены на использовании трюков с перспективой и глубиной в рамках двухмерного пространства. Невозможные в реальном трехмерном пространстве, они действуют на наше зрение, благодаря смещенной перспективе, манипуляциям с глубиной и плоскостью, обманчивым оптическим намекам, несоответствиям планов, игре света и тени, неясным соединениям, благодаря неправильным и противоречивым направлениям и связям.

При изучении темы «Симметрия в пространстве» предлагаю ребятам такие задачи:

Дополняю известные виды симметрии новыми, например, скрытую симметрию наблюдаем, проделывая простой опыт: надо посмотреть на изображение в зеркале, т.е. поменять местами левое и правое. Возьмём зеркало, поставим его ребром на пунктирную линию, а затем посмотрим в него. Что вы наблюдаете?

На картине «Боярыня Морозова» исчезает эффект движения саней, пропадает напряжённость.

На второй картине Питера Брейгеля «Слепые» слепые падают вслед за своим поводырём, а в зеркале – они сами толкают поводыря в речку.

(Мы начинаем разглядывать картину с левого нижнего угла, поэтому впечатление от картины зависит от того, в каком направлении построена композиция.)

1. Задачи на построение сечений.

В немалой степени развитию пространственных представлений способствуют задачи на построение сечений многогранников. Данная тема представлена в школьном курсе геометрии достаточно узко. Ссылаясь на свой опыт и беседу с другими учителями математики, можно утверждать, что уровень изложения материала по теме «Задачи на построение сечений» в школьных учебниках рассчитан на среднего ученика и не соответствует познавательным возможностям учащихся с хорошими способностями к изучению математики. Поэтому её изучению уделяю дополнительное время на консультациях.

Обучение учащихся этой деятельности будет тем эффективнее, чем больше продумана система упражнений, способствующих активному восприятию новых знаний.

За основу была выбрана теория поэтапного формирования умственных действий и знаний, разработанная П.Я. Гальпериным. Руководствуясь этой теорией, изложение темы «Задачи на построение сечений» было разбито на четыре этапа:

1. подготовительный этап;

2. ознакомительный этап;

3. формирующий этап;

4. совершенствующий этап.

Подготовительный этап.

Содержание упражнений должно обеспечивать определенный уровень мыслительной деятельности учащегося и строится по принципу нарастания сложности. Целью подготовительных упражнений является глубокое осмысливание вопросов о взаимном расположении прямых и плоскостей в пространстве, способствующее формированию основных методов построения сечений. Например,

Задача 1. Пересекаются ли прямые МС и РК?

Задача 2. На рисунке точки M, N, P – середины соответственно отрезков DA, DB, DC . Определить взаимное расположение прямых:

а) ND и AB;

б) MP и AC

в) PK и BC;

г) KN и AC

д) MN и AB;

е) MD и BC.

Задача 3. Найти точку пересечения прямой MN с плоскостью основания.

Ознакомительный этап.

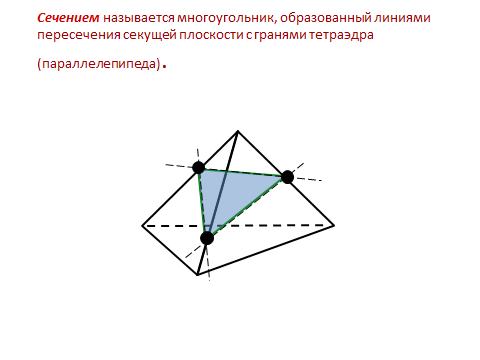
На данном этапе ставится следующая цель: формирование у учащихся понятий секущей плоскости и сечения многогранника; ознакомление школьников с методами построения сечений.

Содержание занятий разбито следующим образом:

1. Введение основных принципов построения простейших сечений.

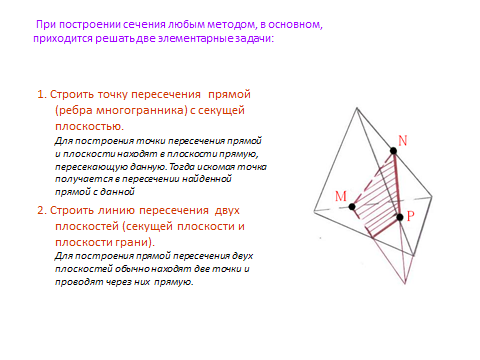
2. Метод построения сечений по трём заданным точкам.

3. Введение метода следов.

Формирующий этап.

Цель данного этапа – систематизировать знания о методах построения сечений, сформировать умение выбора наиболее рационального метода.

Совершенствующий этап.

На совершенствующем этапе продолжается развитие умений построения сечений и применения их при решении различных задач. В этих задачах построение сечений является не конечным результатом решения, а одним из этапов. Это могут быть задачи на нахождение:

1. площади сечения;

2. различных элементов многогранника по известной площади сечения;

3. боковой и полной поверхностей тел по известной площади сечения;

4. отношения площадей поверхности и сечения (Sполн / Sсеч);

5. объема тела, если известна площадь сечения и др.

Так, например, в главе "Объемы тел" мы можем найти задачи следующего содержания:

№ 700 ( Атанасян Л.С.)

В правильной усеченной четырехугольной пирамиде стороны оснований равны 6 см и 4 см, а площадь сечения пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани, равна 15 см². Найдите объем усеченной пирамиды.

При изучении темы "Построение сечений многогранников" на каждом этапе можно рассматривать решение некоторых устных задач из предложенных ниже.

УСТНЫЕ ЗАДАЧИ по теме "СЕЧЕНИЯ МНОГОГРАННИКОВ"

1. Как может быть расположена плоскость относительно многогранника?

2. В каком случае говорят о сечении многогранника плоскостью?

3. Какой фигурой является сечение многогранника плоскостью?

4. В каком случае задача на построение сечения многогранника плоскостью считается решенной?

5. Как может быть задана плоскость сечения?

6. Как найти на чертеже пересечение двух пересекающихся прямых?

7. Как найти на чертеже пересечение прямой и плоскости? Что для этого должно быть задано?

8. Как найти на чертеже пересечение двух плоскостей? Что для этого должно быть задано?

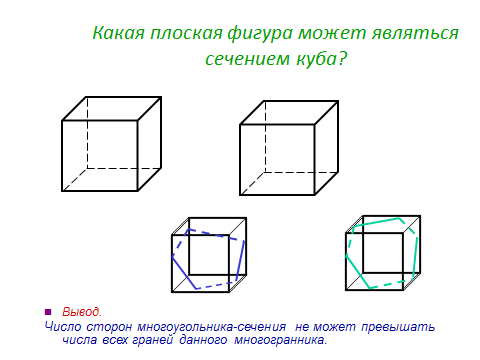
9. Может ли в сечении куба (A…D1) плоскостью получиться: а) квадрат; б) прямоугольник; в) параллелограмм; г) ромб?

10. Может ли в сечении куба плоскостью получиться: а) пятиугольник; б) правильный пятиугольник?

11. Может ли в сечении куба плоскостью получиться: а) шестиугольник; б) правильный шестиугольник?

12. Может ли в сечении куба плоскостью получиться семиугольник? Многоугольник с числом сторон больше шести?

13. Какой многоугольник с наибольшим числом сторон может получиться в сечении: а) тетраэдра; б) четырёхугольной пирамиды; в) шестиугольной призмы; г) n-угольной призмы?

14. Какое сечение призмы называется диагональным?

15. Сколько диагональных сечений у: а) треугольной; б) четырёхугольной; в) пятиугольной; г) n-угольной призмы?

16. Какой фигурой является сечение куба плоскостью, проходящей через концы трёх ребер, исходящих из одной вершины?

17. Возьмите одну из вершин верхнего основания куба. В нижнем основании возьмите проекцию этой вершины. В плоскости нижнего основания возьмите два ребра, исходящие из неё. Проведите плоскость через концы этих рёбер и первую вершину. Какой фигурой будет сечение? Найдите его периметр, если длина ребра куба равна 1.

18. Какой фигурой является сечение куба A…D1 плоскостью, проходящей через вершины В1, D и точку К - середину ребра СС1?

19. Какой фигурой является сечение куба A…D1 плоскостью, проходящей через точки E, F, G - середины соответственно ребер AD, A1B1, B1С1?

20. В какой правильной n-угольной призме все диагональные сечения равны между собой?

21. Определите вид сечения правильной треугольной призмы плоскостью, проходящей через сторону нижнего основания и середину скрещивающейся с ней стороны верхнего основания.

22. Верно ли утверждение о том , что в сечении правильной шестиугольной призмы плоскостью, проходящей через середины двух соседних боковых ребер и вершину верхнего основания, принадлежащей смежной боковой грани, получается равнобедренная трапеция?

23. Может ли прямоугольник быть одним из диагональных сечений наклонной призмы? Приведите пример такой призмы.

24. Найдите площадь сечения куба плоскостью, проходящей через три точки, взятые в серединах его рёбер, выходящих из одной вершины. Длина ребра куба равна 1.

25. Какой фигурой является сечение куба плоскостью, которая проходит через две противоположные вершины нижнего основания и середину одного из ребер верхнего основания? Найдите его периметр, если длина ребра куба равна 1.

26. Какой фигурой является сечение правильного тетраэдра AВСD плоскостью, проходящей через вершину В и точки М, N- середины соответственно сторон AD, СD?

27. Как построить сечение правильного тетраэдра AВСD плоскостью, параллельной грани ВDС и проходящей через точку К - середину ребра AD?

28. Как пересечь правильную треугольную призму тремя плоскостями таким образом, чтобы получилась правильная шестиугольная призма?

12