Развиваем геометрическое мышление, применяя программу "Atelier de Geometrie"

Белорецкая средняя общеобразовательная компьютерная школа

ИКТ в школьном курсе математики

«Развиваем геометрическое мышление, применяя программу “Atelier de Geometrie ”»

Методическая разработка

Автор-составитель: Паньковская Юлия Вадимовна

г.Белорецк

2019г.

Atelier de Geometrie

О необходимости использования ИКТ при изучении геометрии

Компьютерная поддержка курса математики в средней школе создает принципиально новые возможности для обучения – это признается сегодня подавляющим большинством педагогов. Использование ИКТ позволяет обогатить содержание курса и открывает новые активные формы его освоения.

В особой мере это относится к наиболее трудной для понимания математической дисциплине – геометрии. Сокращение в последние годы числа обязательных учебных часов, отведенных на изучение математики вообще и геометрии в частности, привело к резкому снижению как математической культуры в целом, так и ее геометрической составляющей. Известный афоризм – «легких задач по геометрии не бывает» - ежегодно подтверждается на выпускных школьных экзаменах и вступительных испытаниях в вузы.

Хотя бы отчасти компенсировать эти, уже ставшие очевидными потери отечественного образования может, на мой взгляд, разумное использование современных достижений в области ИКТ. Наиболее интересным и эффективным в этом отношении представляется использование так называемых программ-планшетов (интерактивных сред), использующих интерактивное моделирование и конструирование. Наиболее известным в России примером программы такого типа стала «Живая геометрия» - русификация американской программы Geometer's Sketchpad (GSP). Менее известными (и в какой-то мере незаслуженно обойденными вниманием) являются французские Atelier de Geometrie, Cabri Geometre, GeoPlan, GeoSpace и другие.

Все перечисленные программы объединяет наличие трех основных элементов:

• возможность создания на экране интерактивных планиметрических чертежей, напоминающая традиционное построение с помощью циркуля и линейки;

• их «оживление» за счет передвижения свободных точек по плоскости или по определенным линиям с помощью прямого манипулирования мышью;

• измерение длин, углов и других величин с заданной точностью.

Успешность этих программ в обучении объясняется тем, что соединение мыслительной и конструкторско-практической деятельности учащихся позволяет вывести на более высокий уровень, как понимание ими абстрактного математического материала, так и их практическую деятельность, наполнив ее более глубоким содержанием и придав ей элементы настоящего научного исследования.

Для сильных учеников геометрический планшет создает условия, при которых появляется возможность самостоятельно открыть целый ряд геометрических фактов, экспериментально проверить правильность своих гипотез.

Для слабых учеников отставание формально-логического аппарата компенсируется с помощью планшета наглядными зрительными образами геометрических объектов и конструкций, служит надежной опорой для содержательно-практической деятельности.

Вступление

Программа «Atelier de Geometrie» предназначена для поддержки курса геометрии в 7-9 классах основной школы и в 10-11 классах профильной школы. Материалы программы могут использоваться также в 9-х классах для проведения предпрофильного обучения.

Основными целями работы с программой являются:

• создание условий для более глубокого и качественного усвоения учащимися геометрического материала из курса математики основной и полной средней школы;

• получение навыков конструкторско-практической деятельности с использованием современных средств вычислительной техники;

• побуждение учащихся к самостоятельной творческой деятельности с элементами научного исследования.

Не смотря на то, что я сторонник сложившихся многолетних традиций преподавания геометрии в российской школе, понимаю, что компьютер предоставляет принципиально новые возможности при изучении геометрии как школьного предмета и, особенно, в поддержке конструкторской и исследовательской деятельности учащихся. Данная программа вносит в эту деятельность элементы, недоступные без использования современных компьютерных технологий и средств интерактивной графики: на смену пассивному усвоению знаний приходит их активный поиск.

Основным элементом программы и ядром его методической концепции является интерактивная конструкторская среда («геометрический планшет»), имитирующая во многом работу профессиональных графических редакторов и инженерных CAD'ов, учитывающая возрастные особенности учащихся и поставленные образовательные задачи.

Основное назначение программы – создание интерактивных планиметрических чертежей и их исследование. Создание чертежа производится методом прямого манипулирования. При этом используются инструменты, аналогичные традиционным: виртуальные циркуль, линейка, транспортир и т.д. Исследование чертежа происходит через его «оживление» за счет передвижения отельных ключевых точек и связанных с ними фигур. При этом появляется возможность визуально наблюдать за сохранением интересующих ученика соотношений и величин.

Все результаты работы учеников сохраняются и становятся доступны учителю.

Главной методической особенностью программы является соединение мыслительной и конструкторско-практической деятельности учащихся, которое позволяет, на мой взгляд, вывести на более высокий уровень, как понимание абстрактного математического материала, так и практическую деятельность, наполнив ее более глубоким содержанием и придав ей элементы настоящего научного исследования.

Отрицательная сторона работы с программой – она на французском языке. С другой стороны – это еще одна сторона для исследования, для сравнения языков английского и французского.

Цели и планируемые результаты обучения

Использование программы «Atelier de Geometrie» в учебном процессе позволит, на мой взгляд, реализовать следующие образовательные, развивающие и воспитательные цели:

• даст ученику возможность более глубоко овладеть системой геометрических представлений, необходимых для успешного усвоения школьного курса геометрии и в повседневной жизни;

• сделает изучение геометрического материала более осознанным, раскроет творческие способности учащихся; поможет в овладении такими важнейшими методами познания, как анализ и синтез, нахождение закономерностей в геометрических конструкциях, экспериментальной проверке геометрических фактов и гипотез;

• будет способствовать формированию и развитию геометрической интуиции, созданию наглядных образов основных геометрических понятий, развитию навыков конструкторско-практической деятельности, что особенно важно для слабых учащихся, познавательные функции которых остаются долгое время связанными с моторикой;

• поможет воспитанию культуры личности через формирование эстетического вкуса, изучение цвета, ритма при построении геометрических конструкций.

В результате использования программы учащиеся должны прежде всего усвоить необходимый базовый уровень геометрического материала, включенного в обязательный минимум содержания математического образования, т.е. научиться

• распознавать основные геометрические фигуры, выделять их существенные признаки;

• выполнять элементарные геометрические построения с помощью инструментов планшета; изображать геометрические фигуры; выполнять чертежи по условию задачи;

• проводить простейший анализ предлагаемых геометрических моделей и конструкций, различать взаимное расположение фигур;

Кроме того, использование программы позволит (зачастую, за то же самое учебное время) выработать у ученика целый ряд дополнительных умений и навыков:

• проводить экспериментальную проверку изучаемых математических соотношений и закономерностей;

• самостоятельно на основе проведенных математических экспериментов выдвигать предположения и гипотезы;

• с помощью интерактивных чертежей проводить анализ условия задачи и исследование различных случаев;

• используя предлагаемый инструментарий, более осмысленно использовать свойства преобразований при решении геометрических задач;

• решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, идеи симметрии и т.д.

Наконец, в процессе знакомства с программой учащиеся получают возможность приобрести практические навыки работы с современными средствами интерактивной компьютерной графики на доступном им уровне.

Данная программа может использоваться в практике обучения при разном уровне оснащения школы компьютерной техникой. Наиболее оптимальным представляется проведение занятий в кабинете информатики, оснащенном индивидуальными рабочими местами для каждого ученика (пары учеников), связанными в локальную сеть, а также с рабочим местом учителя, компьютер которого подключен к медиапроектору. В этом случае существует возможность максимально использовать ресурсы программы при организации различных форм обучения от фронтальной до индивидуальной.

Для обобщающих или контролирующих уроков по некоторым темам можно использовать данную программу в аудитории, оснащенной одним персональным компьютером, подключенным к медиапроектору. В этой ситуации предпочтительной будет фронтальная форма работы, в рамках которой может быть организована систематизация знаний учащихся (при предъявлении демонстраций) или поставлена общая для всего класса проблемная ситуация.

Единственный компьютер в классе может использоваться учителем для организации групповой деятельности школьников, в процессе которой 2-4 ученика получают общее задание, которое необходимо выполнить, работая за компьютером. В данной ситуации важен не только результат, который получат учащиеся при выполнении заданий, но и способ их взаимодействия в процессе работы. Поэтому учителю необходимо предварительно продумать возможные способы взаимодействия школьников при выполнении такого рода заданий.

При наличии одного или нескольких компьютеров в учебной аудитории учитель имеет возможность организовать также самостоятельную работу некоторых школьников с программой. Это будет эффективно, если учителем будет предлагаться индивидуальная серия заданий для конкретного ученика, нацеленная на коррекцию его типичных ошибок. Кроме того, существует возможность предлагать задания более высокого уровня сложности наиболее успешным школьникам. Таким образом, даже наличие одного или нескольких компьютеров и систематическое использование данной программы на уроках математики может повысить качество обучения.

Методика использования программы в учебном процессе

1. Формы и методы организации учебной деятельности учащихся

На мой взгляд, применение ИКТ в учебном процессе не должно приводить к революционным преобразованиям сложившейся системы обучения. Необходимо, чтобы использование новых средств обучения органично вписывалось в существующую систему организационных форм и методов, расширяя возможности традиционных и закладывая предпосылки для развития новых форм обучения.

Методика использования программы предусматривает все традиционные формы организации обучения, разделенные в зависимости от особенностей коммуникативного взаимодействия между учителем и учащимися на индивидуальную, групповую, коллективную и фронтальную формы. Разумеется, использование ИКТ не может не внести в каждую из этих форм свои особенности как методического, так и организационного плана.

При организации индивидуальной формы обучения программа позволяет учителю выбрать для каждого ученика индивидуальную образовательную траекторию с максимальным учетом его знаний, умений и психологических особенностей. При этом учитель может воспользоваться как набором типовых образовательных траекторий, так и выработать на их основе новую, предназначенную специально для данного ученика. Индивидуальная траектория позволяет определить для каждого ученика не только содержание и уровень сложности изучаемого материала, но и оптимальный темп обучения, индивидуальные критерии оценивания.

При групповой форме организации обучения учитель активно взаимодействует с группой учащихся (2-5 человек), которые в свою очередь общаются друг с другом и имеют общие цели деятельности. В процессе реализации данной формы обучения компьютер и программное обеспечение выступают в качестве инструмента, с помощью которого учениками решается конкретная учебная задача. Важно, чтобы постановка задания для группы учеников соответствовала специфике данной формы, которая состоит в наличии общей цели деятельности. Наиболее полно этой содержательной характеристике групповой формы обучения соответствуют задания исследовательского характера, предполагающие проведение математических экспериментов. После выполнения таких заданий в группах необходимо коллективное обсуждение полученных результатов, их обобщение и подведение итогов работы.

Дальнейшим развитием групповой формы является коллективная форма обучения, при которой учащиеся всего класса рассматриваются как коллектив. Перед классом ставятся общие цели и задачи, достижение которых становится возможным только при активном взаимодействии учащихся друг с другом. Коллективная деятельность, как правило, предполагает разделение функций между учениками при выполнении заданий.

Наиболее полно этим характеристикам коллективной формы обучения соответствуют задания, предполагающие исчерпывающий поиск геометрических объектов или конструкций, обладающих определенными свойствами. Это объясняется тем, что такие задания позволяют ученикам реализовывать все или большинство компонентов учебной деятельности: постановка цели, определение средств ее достижения, планирование деятельности, реализация плана деятельности, распределение ролей, оценка и самооценка результата, подведение итога работы.

При фронтальной форме организации обучения ученики выполняют общее для всех задание в едином, усредненном темпе. Эта форма очень часто используется в практике работы школы, однако при использовании программы к ней целесообразно обращаться лишь изредка и только при наличии в компьютерном классе мультимедийного проектора.

Эта форма оказывается эффективной при демонстрации готовых геометрических конструкций или общих методов их построения.

Наконец, использование программы предполагает проведение учащимися целого ряда самостоятельных домашних работ исследовательского характера. Результатом выполнения такой работы чаще всего становится мультимедийный доклад-демонстрация, включающий найденный фактический и иллюстративный материал, а также результаты собственных исследований.

Проверка и оценивание результатов обучения является существенной составляющей учебного процесса.

Контроль и оценка рассматривается при работе с программой как одно из средств формирования положительных мотивов учения и готовности учеников к самоконтролю. Например, в заданиях на конструирование автоматическая проверка практически невозможна, но ученик вполне способен проверить себя сам: достаточно сравнить «пошевелить» построенный чертеж, чтобы выявить недостающие элементы или допущенные ошибки.

Это повышает объективность оценки, снижает уровень тревожности, прямо или косвенно способствует формированию у каждого ученика адекватной самооценки, освобождает учителя от рутинной работы по проверке выполненных заданий.

В большинстве заданий ученику предоставляется полная свобода в выборе способа их решения и используемого для этого инструментария. Вместо пошаговой подсказки, снижающей степень активности и самостоятельности, предусматривается лишь общая подсказка. Контроль правильности производится при этом по конечному результату.

Некоторые задания носят творческий характер и поэтому могут быть оценены только учителем или даже коллективно всем классом. В этом случае учитель получает доступ к портфелю ученика со своего рабочего места и может не только вынести вердикт о правильности решения, но и внести в него какие-то коррективы, как это делается в традиционном «бумажном» представлении. В некоторых заданиях предусмотрено публичное выступление ученика перед классом с использованием медиапроектора с последующим коллективным обсуждением и оцениванием его результатов.

Задания, выполненные каждым учеником, хранятся в его индивидуальном портфеле – специальной папке на одном из сетевых ресурсов.

Результат выполнения любого задания в программе может быть выведен на печать вместе с историей построения.

Результаты деятельности каждого ученика регистрируются в классном журнале – электронной базе данных, снабженной необходимыми средствами статистического анализа и графического представления результатов.

Классный журнал дает учителю наглядное представление об успешности продвижения каждого ученика по своей образовательной траектории, а также степень усвоения материала в целом по темам и разделам курса геометрии. Это позволяет учителю корректировать индивидуальные образовательные траектории учащихся с учетом накопленного в базе данных опыта, прогнозировать сложность, степень усвоения материала и время на его проработку в будущем.

Таким образом, организация контроля компьютерными средствами не только облегчает труд учителя, но и позволяет повысить качество всего учебного процесса в целом, реализовать принцип индивидуализации обучения.

4. О возможности системного внедрения и активного использования информационных источников сложной структуры (ИИСС) в практике современной российской школы на примере программы «Atelier de Geometrie»

Использование ИИСС возможно при организации обучения по любым существующим в настоящее время образовательным программам и учебникам, т.к. он ориентирован на обязательный минимум содержания математического образования и новые образовательные стандарты по математике 2004 года. Идеология работы с планшетом и методы решения задач универсальны и не ориентированы на какой-то конкретный учебник или систему обучения. Это позволяет пользоваться ИИСС как при работе в рамках традиционной системы обучения, так и в рамках системы развивающего обучения. Кроме того, ИИСС дает богатые возможности, позволяющие расширить содержание школьного математического образования, ориентированные, прежде всего, на развитие интеллектуальных способностей учащихся и повышение мотивации к изучению математики.

Предлагаемая методика работы с программой «Atelier de Geometrie» позволяет успешно использовать ее непосредственно на уроке математики, как в основной, так и в профильной школе.

Программа «Atelier de Geometrie» может функционировать как на домашнем компьютере, так и в любой сети – в пределах школьной локальной сети или сети Интернет.

Работа с программой «Atelier de Geometrie»

Основным назначением планшета является построение интерактивных геометрических чертежей. Процедура получения чертежа во многом напоминает классические задачи на построение с помощью циркуля и линейки - только набор инструментов в планшете несколько шире.

Любая геометрическая конструкция строится из простейших фигур, связанных определенными соотношениями.

Основным достоинством планшета является то, что созданные в нем чертежи являются «живыми»: интерактивное изменение чертежа происходит за счет передвижения точек и фигур с сохранением соответствующих отношений между ними.

1. Построение точек, фигур и макропостроения

Для построения фигуры или макроса нажмите соответствующую кнопку:

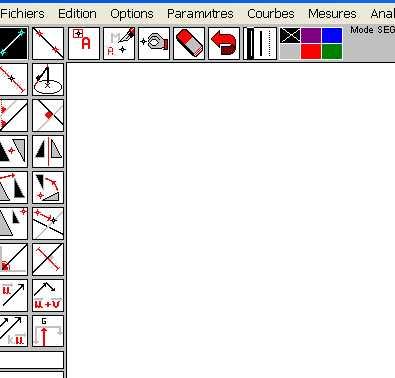
Горизонтальный ряд слева на право (рисунок 1):

Рисунок 1

1. Отрезок

2. Прямая

3. Точка

4. Название точки

5. Оживление чертежа

6. Ластик

7. Отмена последнего действия

8. Выбор толщины линии

9. Выбор цвета

Вертикальный ряд по две клетки слева на право:

1. Середина отрезка (макрос); окружность

2. Параллельные прямые; перпендикулярные прямые (макросы)

3. Центральная симметрия; осевая симметрия

4. Параллельный перенос; поворот

5. Гомотетия; проектирование вдоль прямой

6. Биссектриса угла; серединный перпендикуляр (макросы)

7. Вектор; сумма векторов

8. Умножение вектора на число; центр тяжести (центр моментов)

Дальнейшее построение происходит последовательными щелчками мыши на рабочем чертеже. На первом занятии детей необходимо познакомить с элементарными построениями фигур.

1. «Оживление» чертежей

Как уже говорилось выше, созданные в планшете чертежи можно «оживлять». Вы можете изменять положение любых точек и фигур, участвующих в построении, и следить при этом за изменением конструкции и сохранением интересующих вас соотношений.

По степени свободы передвижения все точки на чертеже делятся на три категории:

• свободные на плоскости (могут свободно перемещаться по всей плоскости);

• свободные на фигурах (могут перемещаться только по фигуре);

• точки пересечения фигур (не могут свободно перемещаться).

О степени свободы любой точки можно судить и по ее виду:

• свободные точки - круг;

• несвободные точки – крест.

Передвижение фигур происходит при перемещении точек, которыми они заданы.

1. Геометрические преобразования

Планшет позволяет выполнять все виды основных геометрических преобразований. Для того чтобы выполнить нужное преобразование, нажмите, например, кнопку .

После этого дальнейшее использование заданного преобразования происходит простым щелчком и «перетягиванием» мыши от точки до прямой, относительно которой данное преобразование происходит.

При изменении чертежа все параметры и построенные образы преобразований изменяются автоматически.

Если же преобразование поворот или гомотетия, то после выбора соответствующей клавиши, появляется функциональное окно, в котором вводятся дополнительные параметры преобразования: угол поворота, коэффициент гомотетии.

1. Измерения

Планшет позволяет производить измерения любых расстояний и углов, имеющихся на чертеже. Для того чтобы провести нужное измерение, необходимо в функциональной строке (рисунок2) выбрать Mesures, появиться окно, в котором вторая группа соответствует измерению отрезков, а третья- измерению углов.

Рисунок 2

Дальнейшее измерение происходит последовательными щелчками мыши по отрезку, длину которого надо узнать. Или «перетягиванием» мыши от одной стороны угла до другой, для измерения его величины.

При изменении чертежа все измерения автоматически пересчитываются.

1. Другие возможности

У планшета огромные возможности. Но открытие их требует кропотливого и усидчивого труда. Своего рода исследовательская деятельность. Ее я предоставляю детям или заинтересовавшимся педагогам.

Примеры заданий для работы с программой

(основная цель построения: при движении картинки все связи между элементами должны сохраняться)

Правильные многоугольники. Поворот.

1. Равносторонний треугольник.

2. Квадрат.

3. Правильный шестиугольник.

4. Правильный пятиугольник.

5. На сторонах выпуклого четырехугольника вне его построены квадраты. Покажите, что расстояния между центрами квадратов, построенных на противоположных сторонах, равны, а отрезки перпендикулярны.

6. На сторонах треугольника вне его построены правильные треугольники. Покажите, что центры этих треугольников являются вершинами правильного треугольника.

7. На сторонах треугольника во внешнюю сторону построены квадраты. Покажите, что прямые, каждая из которых соединяет вершину треугольника с серединой противоположной стороны квадрата, построенного на противоположной стороне треугольника, пересекаются в одной точке.

Биссектрисы. Вписанные и вневписанные окружности.

1. Две вершины треугольника, центр вписанной окружности и центр вневписанной окружности, соответствующий третьей вершине, лежат на одной окружности.

2. В прямоугольном треугольнике центр вписанной окружности, середина катета и точка касания другого катета с вневписанной окружностью лежат на одной прямой.

3. В треугольник АВС вписана окружность, касающаяся сторон АВ и АС в точках D и Е. Покажите, что центр окружности, вписанной в треугольник ADE, принадлежит первой окружности.

4. Биссектрисы углов В и С треугольника АВС пересекаются в точке О. Биссектриса угла С пересекает вторично описанную около треугольника АВС окружность в точке К. Покажите, что АК=КО=КВ.

5. Покажите, что середина высоты треугольника, центр вписанной в него окружности и точка касания стороны, на которую опущена высота, с соответствующей вневписанной окружностью лежат на одной прямой.

Серединные перпендикуляры. Описанная окружность.

1. Точка пересечения серединных перпендикуляров к сторонам треугольника – центр описанной окружности.

2. В окружность вписан четырехугольник ABCD. Точки A₁, B₁, C₁, D₁ являются соответственно серединами дуг AB, BC, CD, DA. Покажите, что прямые A₁C₁ и B₁D₁ перпендикулярны.

3. Около треугольника АВС описана окружность. Биссектрисы его углов А, В, С пересекают эту окружность соответственно в точках А₁, В₁, С₁. Покажите, что прямые АА₁, ВВ₁, СС₁ являются высотами треугольника А₁В₁С₁.

4. Из основания каждой высоты треугольника опущены перпендикуляры на две другие его стороны. Покажите, что основания всех шести перпендикуляров лежат на одной окружности.

5. Прямые АР, ВР, СР пересекают стороны ВС, СА, АВ треугольника АВС соответственно в точках А₁, В₁, С₁. Около треугольника А₁В₁С₁ описана окружность, пересекающая вторично прямые ВС, СА, АВ в точках А₂, В₂, С₂. Покажите, что прямые АА₂, ВВ₂, СС₂ пересекаются в одной точке.

6. Теорема Сальмона. Если через точку окружности проведены три произвольные хорды, на которых как на диаметрах построены окружности, то эти три окружности попарно пересекаются вторично в трех точках, лежащих на одной прямой.

Симметрия. Описанная окружность. Ортоцентр

1. Точка H - ортоцентр треугольника ABC. Покажите, что окружности, описанные около треугольников ABН,BCН,CAН, равны.

2. Покажите, что диаметр описанной около треугольника окружности и его высота, выходящие из одной вершины этого треугольника, симметричны относительно биссектрисы, выходящей из той же вершины.

3. Биссектрисы углов В и С треугольника АВС пересекаются в точке О. Биссектриса угла С пересекает вторично описанную около треугольника АВС окружность в точке К. Покажите, что АК=КО=КВ.

4. Покажите, что точки, симметричные точке, принадлежащей описанной около треугольника окружности, относительно сторон этого треугольника, лежат на прямой, проходящей через ортоцентр этого треугольника.

5. Покажите, что точки, симметричные ортоцентру треугольника относительно его сторон и середин сторон, лежат на описанной около треугольника окружности.

6. Окружность девяти точек.

Изогональное сопряжение.

1. Точка Жергонна

2. Точка Нагеля

3. Точка Лемуана

4. Точка, изогонально сопряженная точке Жергонна.

5. Точка, изогонально сопряженная точке Нагеля.

6. Антиортоцентр.

7. Точка пересечения антибиссектрис.

Геометрические места точек

1. Дана хорда АВ окружности. Рассматриваются всевозможные треугольники АВС, вписанные в эту окружность. Найдите геометрическое место точек пересечения:

а) высот; б) биссектрис треугольника АВС.

2. Точка P перемещается по описанной окружности квадрата ABCD. Прямые AP и BD пересекаются в точке Q, а прямая, проходящая через точку Q параллельно AC, пересекает прямую BP в точке М. Найдите ГМТ М.

3. Найдите множество середин всех отрезков, концы которых лежат на фигуре, являющейся объединением диагоналей квадрата

4. Точка А лежит на окружности с центром О. Найти ГМТ, являющихся серединами всех хорд окружности, проходящих через точку А.

5. На плоскости даны точки А, В, С и D. Постройте ГМТ, состоящее из точек М, из которых отрезок АВ виден под углом в 90°, причем СМ=DМ. Всегда ли есть решение?

6. В плоскости дан разносторонний треугольник АВС. Постойте ГМТ (геометрическое место точек), равноудаленных от точек В и С, а также от прямых АВ и АС.

7. Найдите геометрическое место центров всевозможных окружностей, проходящих через две данные точки A и B.

8. Найдите ГМТ, равноудаленных от

а) сторон данного треугольника;

б) трех данных прямых;

в) трех данных точек.

Результат работы

В завершении своей работы каждый ученик может получить описание своих действий для создания той или иной конструкции. Правильность которой определяется «подвижностью» чертежа. Чертеж считается верным, если при движении объекты «не расползаются». После этого ребенок может распечатать и сохранить свою работу. Например, так.

Вневписанные окружности (рисунок 3).

Составил Деревицкий Илья

N1 : Droite (AB).

N2 : Droite (CD).

N3 : Droite (EF).

N4 : Point G, liй aux deux objets (N3) et (N2) .

N5 : Point H, liй aux deux objets (N2) et (N1) .

N6 : Point I, liй aux deux objets (N3) et (N1) .

N7 : Segment [HG] de longueur: 4.419.

N8: Segment [GI] de longueur: 5.655.

N9 : Segment [IH] de longueur: 3.182.

N10: Bissectrice des deux objets (N8) et (N9) .

N11: Bissectrice des deux objets (N7) et (N9) .

Рисунок 3

N12: Bissectrice des deux objets (N7) et (N8) .

N13: Bissectrice des deux objets (N1) et (N7) .

N14: Bissectrice des deux objets (N1) et (N8) .

N15: Bissectrice des deux objets (N2) et (N8) .

N16: Point J, liй aux deux objets (N13) et (N10) .

N17: Point K, liй aux deux objets (N13) et (N12) .

N18: Point L, liй aux deux objets (N14) et (N11) .

N19: Point M, liй aux deux objets (N14) et (N2) .

N20: Point N, liй aux deux objets (N15) et (N1) .

N21: Perpendiculaire а (N9) passant par O.

N22: Perpendiculaire а (N8) passant par P.

N23: Perpendiculaire а (N2) passant par Q.

N24: Perpendiculaire а (N8) passant par R.

N25: Perpendiculaire а (N1) passant par S.

N26: Perpendiculaire а (N2) passant par T.

N27: Perpendiculaire а (N3) passant par U.

N28: Perpendiculaire а (N7) passant par V.

N29: Perpendiculaire а (N9) passant par W.

N30: Cercle de centre J passant par U.

N31: Cercle de centre K passant par X.

N32: Cercle de centre L passant par Y.

N33: Cercle de centre L passant par D.

N34: Cercle de centre K passant par Z.

N35: Cercle de centre a passant par b.

Правильный пятиугольник (рисунок 4)

Составили: Кострубова Наташа и Муфтиева Даниэла (8 класс)

N1 : Cercle de centre A passant par B.

N2 : Segment [AB] de longueur: 4.573.

N3 : Milieu C du segment [AB].

N4 : Image de (N3) dans la rotation de centre A et d'angle 90.0 degrés.

N5 : Segment [C'A] de longueur: 2.287.

N6 : Segment [C'B] de longueur: 5.113.

N7 : Cercle de centre C' passant par A.

N8 : Cercle de centre B passant par D.

N9 : Segment [BE] de longueur: 2.827.

N10: Image de B dans la rotation de centre E et d'angle -144.0 degrés.

N11: Image de E dans la rotation de centre B' et d'angle -144.0 degrés.

N12: Image de (N10) dans la rotation de centre E' et d'angle -144.0 degrés.

N13: Image de (N11) dans la rotation de centre B" et d'angle -144.0 degrés.

N14: Image de (N12) dans la rotation de centre E" et d'angle -144.0 degrés.

N15: Image de (N13) dans la rotation de centre B0 et d'angle -144.0 degrés.

N16: Image de (N14) dans la rotation de centre E0 et d'angle -144.0 degrés.

N17: Image de (N15) dans la rotation de centre B1 et d'angle -144.0 degrés.

N18: Segment [B"B'] de longueur: 5.377.

N19: Segment [B'B] de longueur: 5.377.

N20: Segment [BB1] de longueur: 5.377.

N21: Segment [B1B0] de longueur: 5.377.

N22: Segment [B0B"] de longueur: 5.377.

Выводы

Проведя несколько курсов со школьниками (6-8 классов), приезжающими из других городов России, я заметила (что подтвердил опрос их сопровождающих), что после общения с данной программой у них повысился интерес к изучению геометрии, что зрительное восприятие чертежа, многовариантность - это не просто слова для них, а реальность. Они научились создавать мультфильм на геометрическую тему, в частности на ГМТ.

Учащиеся нашей школы показали стойкий интерес к предмету, понятливость на уроках, исследовательские способности, желание действовать. Работу я проводила с учениками 7 класса.

«Минусы» - незнание французского языка. Ограничение во времени. Для полного овладения программой необходимо время.