Реализация функциональной грамотности на уроках математики

«Реализация функциональной грамотности на уроках математики»

«Детей надо учить тому,

что пригодится им,

когда они вырастут.»
Аристипп

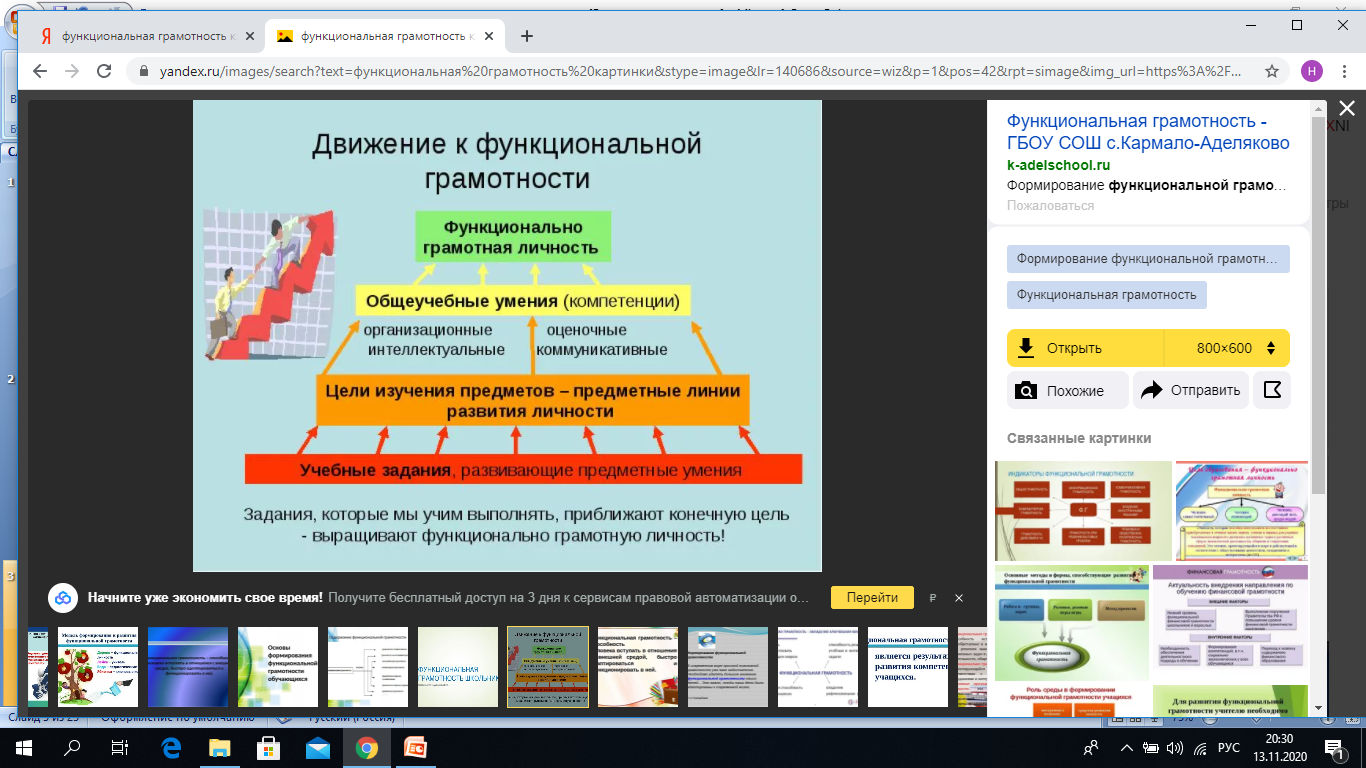
Формирование функциональной грамотности у учащихся становится очень важной целью для любого педагога. При изучении любого учебного предмета есть возможность для формирования и развития функциональной грамотности. В рамках почти любой темы можно поставить   перед учащимся проблемы вне предметной области, которые решались бы с помощью знаний, полученных при изучении того или иного предмета. Математика предоставляет хорошие возможности для рассмотрения подобных задач. На уроках математики чаще, чем на других уроках учащиеся сталкиваются с текстовыми задачами различного содержания и привычным образом составляют модель для применения математических знаний для конкретной задачи.

Что такое функциональная грамотность на уроках математики?

• Функциональная грамотность рассматривается как способность использовать все постоянно приобретаемые в жизни знания, умения и навыки для решения максимально широкого диапазона жизненных задач в различных сферах человеческой деятельности, общения и социальных отношений.

• Функционально грамотная личность – это человек, ориентирующийся в мире и действующий в соответствии с общественными ценностями, ожиданиями и интересами.

• Основные признаки функционально грамотной личности — это человек самостоятельный, познающий и умеющий жить среди людей, обладающий определёнными качествами, ключевыми компетенциями.

Математическая грамотность как компонент функциональной грамотности предполагает способность:

• выявлять проблемы, возникающие в окружающем мире, решаемые посредством математических знаний;

• решать их, используя математические знания и методы;

• обосновывать принятые решения путём математических суждений;

• анализировать использованные методы решения;

• интерпретировать полученные результаты с учётом поставленной задачи.

На уроках функциональной грамотности можно решать следующие задачи.

• Предметные. В условии описывается ситуация, для решения которой требуется установление и использование знаний конкретного учебного предмета.

• Межпредметные. В условии описана ситуация на языке одной из предметных областей с явным или неявным использованием языка другой предметной области. Для решения нужно применять знания из соответствующих областей.

• Практико-ориентированные. В условии описана ситуация, с которой ученик встречается в повседневной своей жизненной практике. Для решения задачи нужно мобилизовать не только теоретические знания из конкретной или разных предметных областей, но и применить знания, приобретённые из повседневного опыта самого обучающегося.

• Ситуационные. Не связаны с непосредственным повседневным опытом обучающегося, но они помогают ему увидеть и понять, как и где могут быть полезны ему в будущем знания из различных предметных областей.

Также на уроках функциональной грамотности можно решать задачи, связанные с развитием читательской, математической и естественно-научной грамотности. Возможно использование калькулятора, для больших и сложных вычислений.

Все учащиеся с большим интересом относятся к таким задачам, не смотря на разный уровень подготовленности.

Задания, как правило, выбираются из открытых источников: материалов международных исследований, демоверсий мониторингов функциональной грамотности, из базы задач ОГЭ (1-5 задания).  

Разберем проблемы, которые возникают при формировании функциональной грамотности на уроках математики.

1. Обучающиеся испытывают затруднения, связанные с избирательным чтением. Они не могут выделить существенную информацию, вопрос и данные, важные для решения задачи.  Нередко можно столкнуться с тем, что ученик, видя нестандартную задачу, не приступал к решению, только из-за того, что его пугает большое количество данных или большой объём текстовой информации. Хотя со стандартными задачами из учебника ученик справляется.  Невнимательность к прочтению условия, непривычность и необычность формулировок пугает обучающихся.  

2.Возникает проблема при формировании математической функциональной грамотности: как сформулировать (переформулировать) задачу, чтобы найти тот математический аппарат, с помощью которого уже можно решить привычную математическую задачу? Оценить математические связи между событиями.

3. Так же немало важная проблема возникает при интерпретации результата, полученного математическими вычислениями, обратный перевод с математического языка на язык решаемой проблемной задачи. Очень часто учащиеся, получив ответ при решении задачи, не задумываются, возможен ли такой результат в реальности. И тогда мы можем получить в ответе: отрицательную строну  квадрата, отрицательную скорость движения  или не целое число строителей и т.п. Распространенная ошибка среди учащиеся  11 класса  при решении 6-го задания  базового уровня  (решения задач на наибольшее/ наименьшее с целыми (по смыслу) ответами), не понимание по смыслу задачи, в какой именно проводиться округление к большему значению, а в какой к меньшему.

 Включая в урок нестандартные задания, множественные тексты, организуя с учащимися различные проекты, учителя таким образом пытаются решить проблему формирования математической функциональной грамотности.  Участие в проектной деятельности одновременно и мотивирует, и учит ребенка работать с информацией, представленной в разных современных источниках, жизненными задачами, переводить их на математический язык и интерпретировать данные. Проекты на уроках математики могут быть связаны с практически значимыми вычислениями, оптимальным выбором, описанием процессов. Преимущество проектной деятельности в том, что большая часть работы происходит вне урока, в самостоятельной мотивированной деятельности ученика во внеурочной деятельности. Это позволяет меньше времени тратить на уроке на решение подобных задач. Но обязательно все результаты проектной деятельности должны быть представлены, хотя бы на уровне класса. Примеры проектов на уроках математики: «Математика и ремонт», «Проценты и кредиты», «Расчеты по химическим уравнениям», «Старинные задачи», «Математика и здоровое питание» и т.п.

Учащиеся, овладевшие математической грамотностью, способны:

• распознавать проблемы, которые возникают в окружающей действительности и могут быть решены средствами математики;

• формулировать эти проблемы на языке математики;

• решать проблемы, используя математические факты и методы;

• анализировать использованные методы решения;

• интерпретировать полученные результаты с учетом поставленной проблемы;

• формулировать и записывать результаты решения.

Формы работы над задачей
1. Работа над решённой задачей.
2. Решение задач разными способами.

3. Представление ситуации, описанной в задачи и её моделирование:
а) с помощью отрезков;

б) с помощью чертежа;

в) с помощью таблицы.

4. Разбивка текста задачи на значимые части.
5. Решение задач с недостающими или лишними данными.

Формы работы над задачей

1. Самостоятельное составление задач учениками.

2 . Изменение вопроса задачи.

3 . Выбор решения из двух предложенных (верного и неверного).

4 . Закончить решение задачи.

5 . Составление аналогичной задачи с измененными данными.

6. Составление и решение обратных задач.

ЭФФЕКТИВНЫЕ ПЕДАГОГИЧЕСКИЕ ПРАКТИКИ

• Создание учебных ситуаций, инициирующих учебную деятельность обучающихся, мотивирующих их на учебную деятельность и проясняющих смыслы этой деятельности;

• Учение в общении, или учебное сотрудничество, задания на работу в парах и малых группах;

• Поисковая активность – задания поискового характера, учебные исследования, проекты;

• Оценочная самостоятельность школьников, задания на само- и взаимооценку, приобретение опыта – кейсы, ролевые игры, диспуты, требующие разрешения проблем, принятия решений, позитивного поведения.

Задача. Менеджер одной компании по продаже газированных напитков заметил, что летом при повышении температуры на один градус продажа напитков увеличивается примерно на 200 литров в день и на столько же она уменьшается на каждый градус понижения температуры. Сегодня он продал 4 600 литров напитка.

• Сколько он может продать завтра, если а) температура повысится на 1^оС; б) станет жарче на 2^оС; в) температура упадет на 1^оС; г) температура не изменится?

• При каком изменении температуры объем продаж напитка не будет превышать 3 000 литров?

• На складе хранится 6 400 литров продукции. К какому наибольшему повышению температуры готова компания?

I этап. Построение математической модели.

Как видно из вопросов задачи, нам необходимо не только определить, сколько менеджер сможет продать завтра газированных напитков при четырех различных условиях (вопрос № 1), но и исследовать различные варианты продажи (вопросы № 2 и № 3). Для решения этой задачи составим общую формулу, которая бы учитывала количество проданного напитка в зависимости от колебания температуры.

Пусть у — количество литров напитка, которое может быть продано завтра. Будем считать, что завтра температура изменится на х градусов. Заметим, что если температура повышается, то х — величина положительная, а если понижается — то отрицательная. Тогда объем продаж изменится на 200х и составит:
у = 4 600 + 200х.
Таким образом, для каждого вопроса задачи можно составить математическую модель:

• «Найти величину у по формуле у = 4 600 + 200х при х равном а)1; б)2; в)–1; г)0».

• «Решить неравенство 4 600 + 200х  3 000».

• «Решить уравнение 4 600 + 200х = 6 400».

II этап. Исследование математической модели.

• Подставляем в формулу у = 4 600 + 200х различные значения для х

• и находим у. Результаты удобно заносить в таблицу.

а) у = 4 600 + 200(+1) = 4 800, 
б) у = 4 600 + 200(+2) = 5 000,
в) у = 4 600 + 200(–1) = 4 400,
г) у = 4 600 + 2000 = 4 600.

• Решаем неравенство 4 600 + 200х  3 000. Получаем 200х  –1 600 или 
  х  –8.

• Решаем уравнение 4 600 + 200х = 6 400. После преобразований получаем 
  200х = 1 800 или х = 9.

III этап. Анализ (интерпретация) результатов.

• Интерпретация результатов этой задачи не вызывает затруднений. Если температура повысится на 1^оС, то можно рассчитывать на продажу 4 800 литров напитка. Если температура повысится на 2^оС, то продажи за следующий день могут достичь 5 000 литров. Понижение температуры на 1^оС сулит сокращение продаж до 4 400 литров. Объемы продаж не изменятся, если завтра не изменится температура.

• Так как х — это изменение температуры, то из полученного нами результата

х  –8 можно сделать вывод, что объем продаж не превысит 3 000 литров при понижении (об этом говорит знак минус) температуры на 8 ^оС и более.

• Компания не будет испытывать недостатка в товаре, даже если температура завтра поднимется на 9 ^оС. Однако, это наибольшее повышение температуры, к которому готова компания по складским запасам.

Запомним одну математическую формулу, которая позволит сформировать у учащихся в процессе изучения математики и других дисциплин качества мышления, необходимые для полноценного функционирования человека в современном обществе.

«ОВЛАДЕНИЕ = УСВОЕНИЕ + ПРИМЕНЕНИЕ ЗНАНИЙ НА ПРАКТИКЕ»

Тема выступления на ШМО учителей математики МОАУ « СОШ №88 г. Орска» учителя математики Рагузиной Ольги Петровны.

4