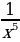Просмотр содержимого документа
«Реферат на тему" Функция вида y=x^-(2n+1)»
Реферат
На тему: функция вида y=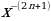 .
.
Если показатель степени равен отрицательному нечетному числу, то такую функцию можно назвать степенной с нечетным отрицательным показателем. Общая формула для таких функций выглядит как y = х-2n-1, где n – любое натуральное число. Функция вида y=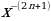 – нечетная функция. Так же данный график функции можно представить в виде y=
– нечетная функция. Так же данный график функции можно представить в виде y=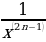 . Примерами таких функций могут служить y = x-3, y=x-9, y=х-139.
. Примерами таких функций могут служить y = x-3, y=x-9, y=х-139.
График функции y=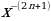
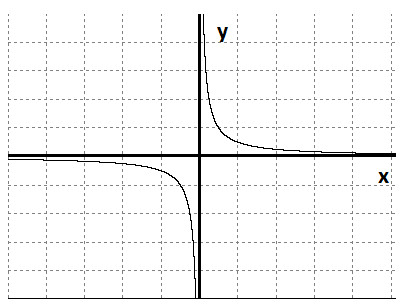
Свойства функции:
1) D(y)=(-∞;0)U(0;+∞).
2) Нечетная функция.
3) Убывает на (-∞;0)U(0;+∞).
4) Не ограничена.
5) Наименьшего и наибольшего значения нет.
6) Функция непрерывна на открытых лучах (-∞;0)U(0;+∞).
7) Е(у)=(-∞;0)U(0;+∞).
8) Выпукла вверх на (-∞;0), выпукла вниз на (0;+∞).
Отметим, что ось x является горизонтальной асимптотой графика функции y=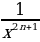 , а ось y является вертикальной асимптотой этого графика.
, а ось y является вертикальной асимптотой этого графика.
Рассмотрим график функции вида y=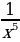
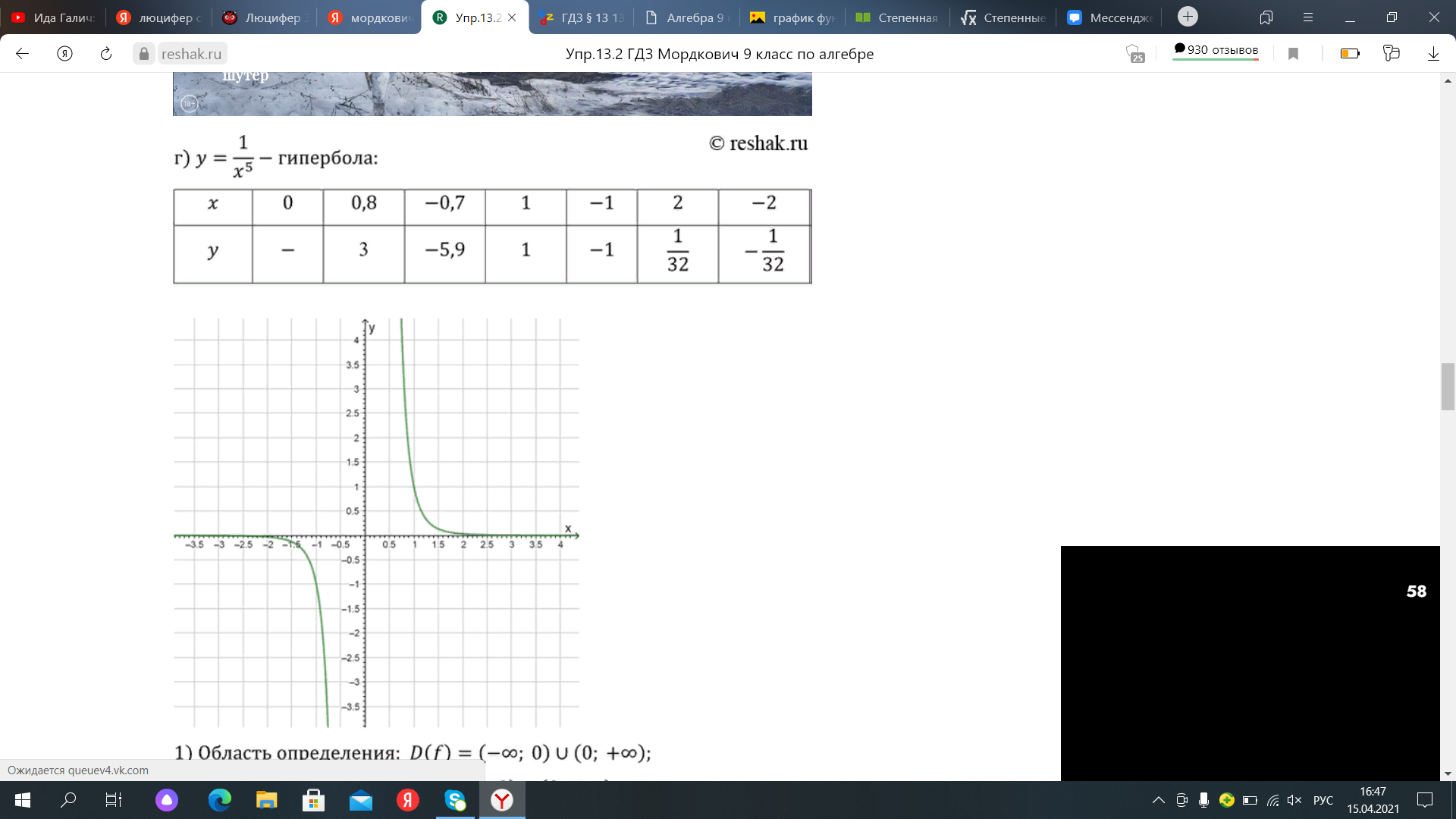
Свойства функции:
1) D(y)=(-∞;0)U(0;+∞).
2) Нечетная функция.
3) Убывает на (-∞;0)U(0;+∞).
4) Не ограничена.
5) Наименьшего и наибольшего значения нет.
6) Функция непрерывна на открытых лучах (-∞;0)U(0;+∞).
7) Е(у)=(-∞;0)U(0;+∞).
8) Выпукла вверх на (-∞;0), выпукла вниз на (0;+∞).
Применение функции с нечетным целым показателем
Во времена второй мировой войны Гиперболы применялись для определения местоположения. На двух радиостанция одновременно испускалось два радиосигнала, человек определяющий своё местоположение расчитывал время между приходом каждого из этих дух сигналов, после чего строил на карте две гиперболы. Местом их пересечения и было его дислокация.
Гипербола обладает оптическим свойством, которое описывается следующим образом: луч, исходящий из источника света, находящегося в одном из фокусов гиперболы, после отражения движется так, как будто он исходит из другого фокуса.
Это свойство используется в антеннах Кассегрена

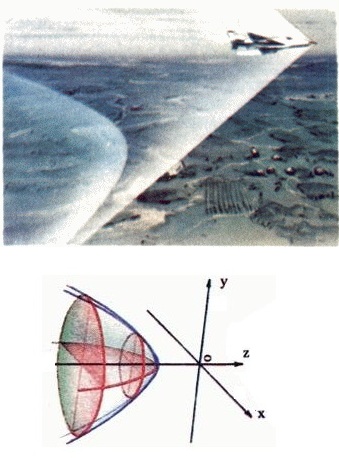
Еще пример зона слышимости звука пролетающего самолета. Если самолет движется со сверхзвуковой скоростью, то в воздухе зона слышимости образует трехмерную поверхность – гиперболоид вращения.
Так же гипербола очень часто встречается в природе.


Список литературы:
1. http://www.algebraclass.ru/kubicheskaya-funkciya/ дата обращения 13.04.2021 г.
2. http://fizmat.by/math/function/quadratic_function/ дата обращения 13.04.2021 г.
3. http://www.yaklass.ru/p/algebra/9-klass/chislovye-funktcii-9132/stepennaia-funktciia-s-naturalnym-pokazatelem-12044/re-c7626d3e-e29a-41e9-970f-1a5540f90427/ дата обращения 13.04.2021 г.
4. Математический энциклопедический словарь./ Гл. ред. Ю.В. Прохоров; Ред. кол.: С.И. Адян, Н.С. Бахвалов, В.И. Битюцков, А.П. Ершов, Л.Д. Кудрявцев, А.Л. Онищик, А.П. Юшкевич.- М.: Сов. энциклопедия, 1988. - 847 с.







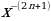 .
.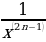 . Примерами таких функций могут служить y = x-3, y=x-9, y=х-139.
. Примерами таких функций могут служить y = x-3, y=x-9, y=х-139.
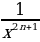 , а ось y является вертикальной асимптотой этого графика.
, а ось y является вертикальной асимптотой этого графика.