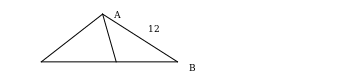Уровневая технология на уроках математики в 9классе.
Тема: Релейный зачет по теме «Признаки подобия треугольников»
Общая целевая установка:
Создание условий для продвижения учащихся в соответствии с их способностями и возможностями по собственной траектории развития;
Обучение правильному оцениванию своих знаний.
Технология: уровневая.
Планируемый результат: возможность выхода на более высокий качественный уровень развития в соответствии со способностями и возможностями по собственной траектории.
Организация работы: в виде групп по трем уровням.
Релейный зачет по теме «Признаки подобия треугольников»
Место урока: заключительный урок по данной теме.
Когнитивная цель урока: обобщить и систематизировать знания, умения, навыки по теме «Признаки подобия треугольников» определить индивидуальные уровни усвоения учебного материала по теме.
Применяемые формы обучения: фронтальная, индивидуальная.
Методы обучения: поисковый, практический, самопроверка.
Оборудование и материалы: карточка-справочник, чертежные принадлежности, таблица учета знаний, задания 1 уровня сложности, задания 2 уровня сложности, задания 3 уровня сложности, дополнительные задания, презентация темы, экран, ноутбук, мультимедийный проектор, приложение к уроку: (Презентация.) – на электронном носителе.
Ход урока
Презентация
1.Организационно-мотивирующий. Начало показа слайдов. (Презентация. Слайды 1-3.)
Ребята, сегодня мы повторяем тему «Признаки подобия треугольников». И наша задача на уроке обобщить и систематизировать знания теоретического материала, умения и навыки решения задач по теме.
И наш урок я начну словами древнегреческого поэта Нивея: «Математику нельзя изучать, наблюдая, как это делает сосед». Поэтому хотелось бы, что бы вы сегодня работали в полную силу.
2. Повторение. (Презентация. Слайды 4-5.)
Повторение пройденной темы мы начнем с небольшой разминки. Это поможет вам настроиться на работу и повторить теоретический материал. Готовы? Тогда начнем. Поиграем в игру «Найди ошибку». Вы будете зачитывать показанное на экране утверждение, находить ошибку и исправлять ее. Не забудьте, на столе у вас лежит «Таблица учета знаний», куда вы будете вносить свою оценку за каждый этап урока. В конце урока вы подведете итог своей работы и выставите себе отметку.
3. Решение задач по готовому чертежу. (Презентация. Слайды 6-7.)
Заученный материал мы повторили, а, теперь переходя ко второму этапу урока, покажите, как вы умеете размышлять. Решаем задачи устно по готовому чертежу.
3. Физкультминутка. (Презентация. Слайд 8.)
Давайте немножко отдохнем и дадим отдых глазам. Вы будете выполнять упражнения, которые повышают мыслительную деятельность, синхронизируют работу полушарий, способствуют улучшению запоминания, повышают устойчивость внимания, облегчают процесс письма.
4. Самостоятельная работа. (Презентация. Слайды 9-15.)
У вас на столе лежат карточки по каждому из признаков подобия треугольников. Они разделяются на три группы-уровня:
1 уровень – карточки с относительно простыми заданиями ( синий цвет шрифта).
2 уровень – с заданиями достаточного уровня (зеленый цвет шрифта).
3 уровень – с заданиями повышенного уровня (красный цвет шрифта).
Карточки с дополнительными заданиями не делятся по уровням (черный цвет шрифта). Необходимо решить как можно больше задач, причем желательно показать умение решать задачи повышенного уровня сложности. Учащийся, выполнивший первое задание, пишет в «Таблице учета знаний» «+», «±» или «-». Затем вы выбираете себе новое задание . Если какой-то тип задач показался вам слишком сложным, но вы хотите в нем разобраться, то можете спросить у меня карточку с образцом решения аналогичного задания.
5.Рефлексия.
Анализируется работа на уроке, разбираются наиболее каверзные задания, дается оценка работы каждого: подводятся итоги, выставляется дифференцированная итоговая оценка (например, если ученик хорошо решил все задачи второго уровня, но не пытался поработать на 3 уровне, то ему выставляется отметка «6»).Заполняется карточка
Знаю хорошо:
Нужно узнать больше об:
Непонятно:
6. Домашнее задание. (Презентация. Слайд 16.)
Учебник. Глава 3 § 1-5 Вопросы 1-22 , с. 174.
Выбрать для домашней работы 2-3 карточки, задания которых не успел решить на уроке.
Приложение.
Игра «Найди ошибку».
Тема: «Подобные фигуры».
Если две стороны одного треугольника пропорциональны двум сторонам второго треугольника, то такие треугольники подобны.
Отношение площадей подобных треугольников равно коэффициенту подобия.
Если два угла одного треугольника равны двум углам второго треугольника, то такие треугольники равны.
Отношение периметров подобных треугольников равно коэффициенту подобия.
Медианы треугольника делятся точкой пересечения в отношении 1:2, считая от вершины.
Если две стороны одного треугольника равны двум сторонам другого треугольника и углы, заключенные между этими сторонами равны, то такие треугольники подобны.
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сторонам другого треугольника.
Параллельные прямые пересекающие стороны угла, отсекают на его сторонах равные отрезки.
Биссектриса треугольника делит противолежащую сторону в таком отношении, в каком находятся прилежащие стороны.
Задания 1 уровня сложности
Первый признак подобия треугольников.
Два треугольника подобны. Два угла одного из этих треугольников равны 100º и 60º. Чему равны углы второго треугольника?
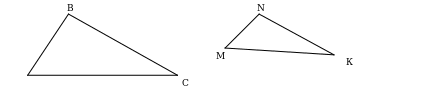
А
Даны подобные треугольники АВС и МКТ, ∟А=∟М, ∟В=∟К. Назовите пары сходственных сторон этих треугольников.
Второй и третий признаки подобия треугольников.
Докажите подобие треугольников, если ∟А = ∟К = 90º.
С
А
25
К
Р
6
2. Дано: ∟В=∟Е. Доказать: ∟А = ∟D.
А
С
D
Р
Задания 2 уровня сложности
Первый признак подобия треугольников.
1.Дано: ∟В = ∟D. Доказать: ΔАОD подобен ΔCОD .
ΔCОD .

А
О
С
D
2. Дано: АВСD – трапеция. Найдите на рисунке подобные треугольники и докажите их подобие.
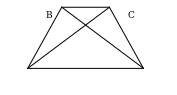
А
D
Второй и третий признаки подобия треугольников.
1
А
С
М
К
18
36
. Подобны ли треугольники АВС и МРК
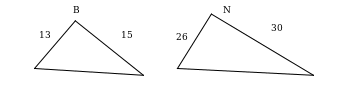
2. Отрезок СD – высота, проведенная к гипотенузе АВ прямоугольного треугольника АСВ. Доказать, что треугольник АDС подобен треугольнику СDВ.
Задания 3 уровня сложности.
Первый признак подобия треугольников.
Д
A
D
ано: АВСD – трапеция. Найдите на рисунке подобные треугольники и докажите их подобие. 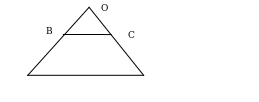
2. АВСD – параллелограмм, DN ┴АВ, DF┴ВС, АВ =5, DN =4, DC= 3,5. Найдите: FD.
Второй и третий признаки подобия треугольников.
1
С
D
7
9
.
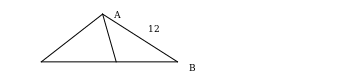
Доказать, что треугольник АВС подобен треугольнику DВА.
2. Длины оснований трапеции равны 2 и 4 см, а ее высота – 3 см. Вычислите расстояния от точки пересечения диагоналей трапеции до прямых, содержащих ее основания.
Дополнительные задания
Для измерения ширины реки построены два подобных треугольника. По данным чертежа определить ширину реки (АС = 10 м, АD = 9 м, DE = 8 м). Ответ: 36 м
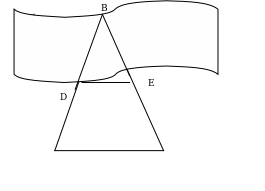
A
C
Наблюдательный пункт находится в точке В на высоте АВ = 10м. На расстоянии АС = 500 м от него поставлен щит СD= 2 м. Определить ширину полосы ЕС, которая не видна наблюдателю.
Ответ: 125 м.
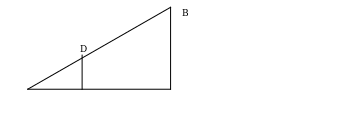
Е
C
A
Лист контроля знаний по теме «Признаки подобия треугольников».
| Вопрос | Номер страницы |
| 1. Что называется отношением отрезков? | 114 |
| 2. Какие треугольники называются подобными? | 115 |
| 3. Чему равно отношение площадей подобных треугольников? | 117 |
| 4. В каком отношении биссектриса треугольника делит его противолежащую сторону? | 118 |
| 5. Сформулируйте первый признак подобия треугольников. | 123 |
| 6. Сформулируйте обобщенную теорему Фалеса. | 125 |
| 7. Сформулируйте второй признак подобия треугольников. | 131 |
| 8. Сформулируйте третий признак подобия треугольников. | 132 |
| 9. Какие многоугольники называются подобными? | 134 |
| 10. Чему равно отношение площадей подобных многоугольников? | 135 |
| 11. В каком отношении точка пересечения медиан треугольника делит каждую из медиан? | 133 |
| 12. Каким свойством обладает высота, проведенная к гипотенузе прямоугольного треугольника? | 144 |
| 13. Чему равен квадрат длины высоты, проведенной к гипотенузе прямоугольного треугольника? | 145 |
| 14. Что называется синусом острого угла прямоугольного треугольника? | 157 |
| 15. Что называется косинусом острого угла прямоугольного треугольника? | 157 |
| 16. Что называется тангенсом (котангенсом) острого угла прямоугольного треугольника? | 158 |
| 17. Как изменяется синус острого угла при возрастании этого угла? | 162 |
| 18. Как изменяется косинус острого угла при возрастании этого угла? | 162 |