Занятие 56. Тема «Дифференциальные уравнения с разделяющимися переменными»
План лекции:
Понятие ДУ с разделяющимися переменными
Метод решения ДУ с разделяющимися переменными
Решение задачи Коши
Понятие ДУ с разделяющимися переменными
Среди обыкновенных дифференциальных уравнений первого порядка существуют такие, в которых возможно переменные x и y разнести по разные стороны знака равенства. В уравнениях вида 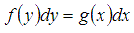 переменные уже разделены, а в уравнении
переменные уже разделены, а в уравнении 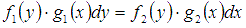 переменные разделяются посредством преобразований. Кроме того, некоторые дифференциальные уравнения сводятся к уравнениям с разделяющимися переменными после введения новых переменных.
переменные разделяются посредством преобразований. Кроме того, некоторые дифференциальные уравнения сводятся к уравнениям с разделяющимися переменными после введения новых переменных.
Определение. Дифференциальные уравнения 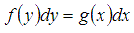 , а также уравнение
, а также уравнение 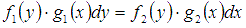 называют уравнениями с разделенными переменными.
называют уравнениями с разделенными переменными.
Название этого вида дифференциальных уравнений достаточно показательно: выражения, содержащие переменные x и y, разделены знаком равенства, то есть, находятся по разные стороны от него.
Будем считать, что функции f(y) и g(x) непрерывны.
Метод решения ДУ с разделяющимися переменными
Уравнение вида 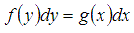 решается методом интегрирования обеих частей уравнения, при этом число С ставится в правой части, где переменная х. То есть
решается методом интегрирования обеих частей уравнения, при этом число С ставится в правой части, где переменная х. То есть 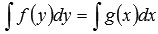 . Интегралы вычисляются определенным методом интегрирования, которые мы с вами изучили.
. Интегралы вычисляются определенным методом интегрирования, которые мы с вами изучили.
Пример1. Найти общее решение ДУ с разделяющимися переменными
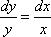
Решение. Проинтегрируем обе части уравнения 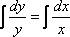
Интегралы табличные, поэтому решение будет следующим 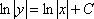 - это общий интеграл дифференциального уравнения, который записывается в ответ.
- это общий интеграл дифференциального уравнения, который записывается в ответ.
Пример2. Найдите общее решение дифференциального уравнения с разделенными переменными 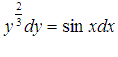 .
.
Решение: Проинтегрируем обе части равенства: 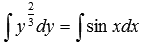 . По сути, мы уже получили общее решение исходного дифференциального уравнения, так как свели задачу решения дифференциального уравнения к уже известной задаче нахождения неопределенных интегралов. Однако, эти неопределенные интегралы выражаются в элементарных функциях, и мы можем взять их, используя таблицу первообразных:
. По сути, мы уже получили общее решение исходного дифференциального уравнения, так как свели задачу решения дифференциального уравнения к уже известной задаче нахождения неопределенных интегралов. Однако, эти неопределенные интегралы выражаются в элементарных функциях, и мы можем взять их, используя таблицу первообразных:
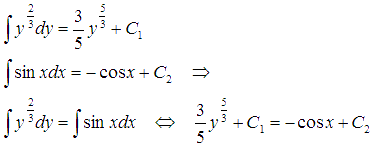
где С1 и С2 – произвольные постоянные.
Мы пришли к неявно заданной функции 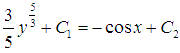 , которая является общим решением исходного дифференциального уравнения с разделенными переменными. Ответ можно оставить в таком виде.
, которая является общим решением исходного дифференциального уравнения с разделенными переменными. Ответ можно оставить в таком виде.
Уравнение вида 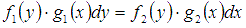 для начала преобразовывается следующим образом: все, что содержит у перенести в левую часть, а все, что содержит х перенести в правую часть, то есть разделить переменные по сторонам. В итоге получим уравнение первого вида
для начала преобразовывается следующим образом: все, что содержит у перенести в левую часть, а все, что содержит х перенести в правую часть, то есть разделить переменные по сторонам. В итоге получим уравнение первого вида
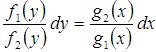
При разделении переменных следует быть очень внимательными, чтобы проводимые преобразования были эквивалентными (чтобы f2(y) и g1(x) не обращались в ноль на интервале интегрирования). В противном случае можно потерять некоторые решения. Разберемся с этим на примере.
Пример 3. Найти все решения дифференциального уравнения 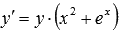
Решение: Это уравнение с разделяющимися переменными, так как мы можем разделить x и y:

Для нулевой функции y исходное уравнение обращается в тождество
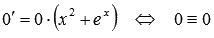 , поэтому, y=0 является решением дифференциального уравнения. Это решение мы могли упустить из виду.
, поэтому, y=0 является решением дифференциального уравнения. Это решение мы могли упустить из виду.
Проинтегрируем дифференциальное уравнение с разделенными переменными
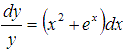
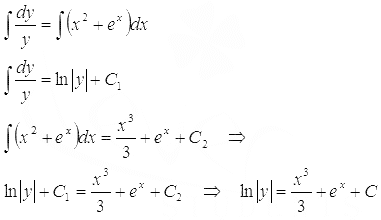
В преобразованиях мы заменили C2 - C1 на С.
Мы получили решение ДУ в виде неявно заданной функции 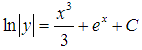
Ответить на контрольные вопросы:
Что называется дифференциальным уравнением?
Перечислите виды ДУ.
Что значит решение дифференциального уравнения?
Назовите виды решений ДУ.
Как решается диф.уравнение?
Пользуясь этим и теоретическим материалом учебника П.Е. Данко «Высшая математика в упражнениях и задачах» часть 2 глава IV §1 п.2 стр.118, разобрать №507, №510 и найти общее решение ДУ 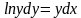 и решить задачу Коши при условии у(1)=2.
и решить задачу Коши при условии у(1)=2.







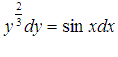 .
. 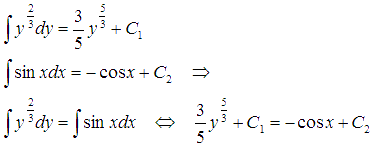
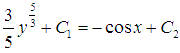 , которая является общим решением исходного дифференциального уравнения с разделенными переменными. Ответ можно оставить в таком виде.
, которая является общим решением исходного дифференциального уравнения с разделенными переменными. Ответ можно оставить в таком виде. 
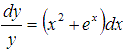
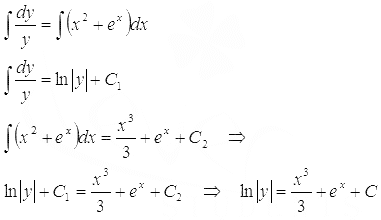
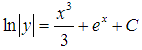
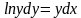 и решить задачу Коши при условии у(1)=2.
и решить задачу Коши при условии у(1)=2. 









