Решение комбинаторных задач практического содержания

Разработка учебного занятия по формированию функциональной грамотности

Тема: «Решение комбинаторных задач практического содержания»

Класс – 5

Тип занятия: урок открытия новых знаний, обретения новых умений и навыков

Цель: формирование функциональной грамотности учащихся с помощью умения решать комбинаторные задачи различными способами.

Задачи:

Образовательная:

- решение комбинаторных задач с помощью «дерева возможных вариантов»;

- усиление прикладной направленности;

- повторить и обобщить метод перебора при решении комбинаторных задач, познакомить с методом решения составлением «дерева возможных вари антов», правилом умножения;

- формирование функциональной грамотности учащихся.

Учащиеся должны уметь:

- выделять комбинаторные задачи из ряда предложенных;

- решать комбинаторные задачи;

- выработать умение применять математическую теорию в конкретных ситуациях;

Воспитательная:

- добиться понимания практической значимости умения решать задачи;

- способствовать формированию у учащихся определенного набора экономических компетенций в сфере познавательной деятельности, трудовой и бытовой сферах, социальной деятельности, связанных с решением задач;

- способствовать формированию значимых качеств личности: трудолюбие,

дисциплинированность, ответственность, гражданские качества личности, бережливость, экономность, деловитость, толерантность, предприимчивость, самостоятельности в принятии решений через решение задач;

Развивающая:

- развивать математическое мышление, интерес к предмету, познавательную и творческую деятельность учащихся, математическую речь, умение самостоятельно добывать знания;

- способствовать совершенствованию операций умственной деятельности: анализ, синтез, классификация, способность наблюдать и делать выводы, выделять существенные признаки.

Познавательные УУД:

- уметь искать информацию в задачниках, интернете, ориентироваться в своей системе знаний.

Регулятивные УУД:

- уметь определять и формулировать цель на уроке с помощью учителя, оценивать правильность выполнения действий на уровне адекватной оценки, планировать свои действия и вносить в них коррективы при необходимости, высказывать своё предположение.

Личностные УУД:

- способность к самооценке на основе критерия успешности учебной деятельности.

Коммуникативные УУД:

- уметь слушать и слышать, уметь работать в группе, сотрудничать в совместном решении проблемы.

Планируемые результаты:

Предметные:

- уметь решать комбинаторные задачи с практическим содержанием.

Метапредметные:

- уметь соотносить предметный материал с жизненными ситуациями;

- уметь анализировать задачу;

- уметь высказать свою точку зрения, сделать вывод.

Личностные

- формирование устойчивой мотивации к обучению.

ХОД ЗАНЯТИЯ:

1. Мотивация (самоопределение) к учебной деятельности.

Проверка готовности учащихся к занятию.

Здравствуйте, ребята! Рада видеть вас.

II. Актуализация и фиксирование индивидуального затруднения в пробном действии.

- В старинных русских сказаниях повествуется, как богатырь, доехав до распутья, читает на камне: “Прямо поедешь – голову сложишь, направо поедешь – коня потеряешь, налево поедешь – меча лишишься”. Ребята, с какой проблемой сталкивается добрый молодец на перепутье? (с проблемой выбора дальнейшего пути движения)

- Верно! А дальше уже говорится, как он выходит из того положения, в которое попал в результате выбора. Но выбирать разные пути или варианты приходится и современному человеку.

Приведите примеры, когда нам приходится делать выбор?

………………

Оказывается, существует целый раздел математики, который занят поисками ответов на эти вопросы. И называется он - комбинаторика.

- А как вы понимаете, что такое комбинаторика? (ответы учащихся)

Комбинаторика – это раздел математики, в котором изучается, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.

Исторические сведения

Комбинаторика - ветвь математики, изучающая комбинации и перестановки предметов, возникла в XVII веке. Долгое время комбинаторика лежала вне основного русла развития математики. Положение дел резко изменилось после появления быстродействующих вычислительных машин. В настоящее время комбинаторные методы применяются в теории случайных процессов, статистике, математическом программировании, вычислительной математике и др.

- Тема нашего урока называется «Решение комбинаторных задач». Откройте тетради, запишите число и тему урока.

III. Выявление места и причины затруднений-

Задачи, которые мы сегодня будем решать, помогут вам творить, думать необычно, оригинально, смело. Видеть то, мимо чего вы часто проходили не замечая, любить неизвестное, новое, преодолевать трудности.

- И еще сегодня в очередной раз убедимся, что наш мир полон математики, и продолжим исследование на предмет выявления математики вокруг нас.

Работаем в парах.

Задача №1. На каждой парте по три кубика: красный, жёлтый и синий. Необходимо составить из трех одинаковых по размеру кубиков красного, желтого и синего цвета несколько отличающихся друг от друга построек.

(Дети хаотично переставляют кубики, считают, сколько различных вариантов получилось). На первый стол выносят все шесть вариантов. Необходимо поставить их так, чтобы рядом были постройки с одинаковыми нижними кубиками.

- Обычный вопрос в комбинаторных задачах – это «Сколькими способами…?» или «Сколько вариантов…?»

Ответ: 6 вариантов.

Итак, при решении этой задачи мы искали способ перебора возможных вариантов. Во многих случаях оказывается полезным прием?

Нет, можно упустить вариант.

Способ построения картинки – схемы перебора вариантов, дерево возможных вариантов. Это, во – первых, наглядно, во- вторых, позволяет нам все учесть, ничего не пропустить.

*

К Ж С

Ж С К С К Ж

С Ж С К Ж К

Варианты КЖС, КСЖ,ЖКС, ЖСК,СКЖ, СЖК. Этот метод называется - “Дерево возможных вариантов”.

Ответ: 6 вариантов.

Найдем правило решения таких задач путем логического рассуждения.

Разберем на примере цветных кубиков. Возьмем красную полоску – её можно переставить 3 раза, возьмем синюю полоску – её можно переставить только 2 раза, т.к. одно из мест уже занято красной, возьмем желтую полоску – её можно положить только 1 раз.

ИТОГО: 3 х 2 х 1=6.

Правило умножения: если первый элемент в комбинации можно выбрать а способами, после чего второй элемент – b способами, то общее число комбинаций будет равно а х b.

Задача №2 Решите данную задачу различными известными уже вам способами. Работают индивидуально, фронтальная проверка.

Решение: 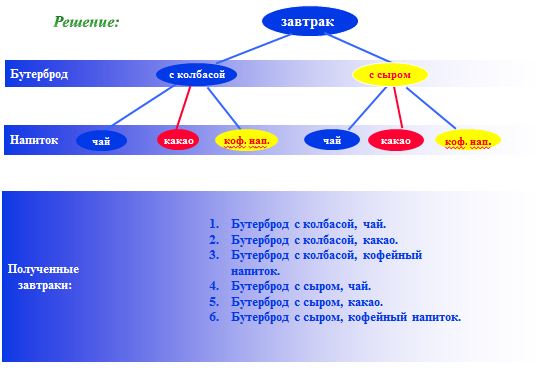Ответ: 6 вариантов завтрака.

За́втрак — первый дневной приём пищи, утренняя еда; пища, приготовленная для утренней еды. Ученые пришли к выводу: дети, которые получают полноценный завтрак, лучше развиваются, более успешны в учебе, у них реже встречаются угнетенные состояния, приступы беспокойства и гиперреактивности.

Таким образом, завтрак влияет на работоспособность, являясь для детей настоящей «пищей для мозга».

Установлено, что определенные продукты могут стимулировать умственную деятельность. Основное средство для поддержания работоспособности мозга - глюкоза. Поэтому в рационе много и напряженно занимающегося школьника должно быть что-то сладкое: чай с сахаром, сладкий творожок, небольшой кусочек шоколадки. Конечно, злоупотреблять сладким не стоит, но в период экзаменов или большой нагрузки можно сделать исключение.

У завтрака еще одна важная функция - воспитательная: благодаря завтракам у детей постепенно вырабатывается привычка своевременно и правильно питаться. А это позволит им в будущем избежать проблем со здоровьем и лишним весом.

Специалисты считают, что завтрак для ребенка должен состоять из трех основных элементов: фруктов, зерновых и молочных продуктов.

IV Физминутка

V Закрепление (работа в группах)

Задача для группы № 1:

В гардеробе у Алексея есть 3 рубашки, джинсы (классика), 2 брюк (по цвету подходят к любой рубашке), кроссовки и туфли. Сколько дней подряд у Алексея будет новый облик, если джинсы классика допустимы школьным дресс - кодом, а Алексей убежден, что кроссовки и брюки – не сочетаемы.

Задача для группы № 2: В пиццерии всегда можно получить пиццу с двумя обязательными начинками: сыром и помидорами. Но можно заказать пиццу по своему рецепту с дополнительными начинками. Вы можете выбрать из четырех различных дополнительных начинок: оливок, ветчины, грибов и колбасы.

Вера с друзьями вегетарианцами решила заказать 2 вегетарианских пиццы и одну для себя.

Сколько вариантов различных комбинаций у Веры и ее друзей из предлагаемых дополнительных начинок?

Разбор задачи, решение и проверка.

VI Подведение итогов урока (что узнали нового, что было сложным, новым, интересным и др.).

VII Домашнее задание, выставление отметок за урок.

Решить задачу:

Вера творческая натура. На день рождения ей подарили набор для творчества. Она планирует изготовить браслеты.

Сколько вариантов браслетов может изготовить Вера, если она будет использовать все цвета перламутровых бусин для изготовления браслета, как показан на рисунке?

- Спасибо за работу! До новых встреч!