Тема урока: «Решение комбинаторных задач. Сочетания»
Место урока в учебном плане: «Комбинаторика. Случайные события» урок 2/8.
Тип урока: комбинированный
Цели урока:
Образовательные:
ознакомить с типами задач на сочетания их решения;
сформировать умения решать задачи на сочетания различными методами,
продолжить формирование навыков решения задач на перестановки.
Развивающие:
познавательного интереса учащихся,
памяти, внимания,
умения сравнивать и анализировать,
Воспитательные:
трудолюбия,
культуры учебного труда,
культуры речи, самостоятельности,
умения работать в коллективе.
Методы обучения: объяснительно-иллюстративный, частично-поисковый,.
Формы познавательной деятельности учащихся: фронтальная, индивидуальная.
УМК: Математика: учебник для 6 кл. под редакцией Г.В.Дорофеева, И.Ф.Шарыгина и др., изд-во «Просвещение», 2008 г.; Математика, 5-6 : кн. для учителя / [С. Б. Суворова, [ Л. В. Кузнецова, С. С. Минаева, Л. О. Рослова]. — М. : Просвещение, 2006.
Оборудование: ПК или ноутбук, проектор, экран, презентация к уроку..
Программное обеспечение: ОС Windows, MS Power Point, презентация к уроку.
Дидактический материал: карточки для самостоятельной работы, карточки для работы на доске.
Литература:
Математика : учеб. для 6 кл. общеобразоват. учреждений/ Г. В. Дорофеев, И. Ф. Шарыгин, С. Б. Суворова и др.]; под ред. Г. В. Дорофеева, И. Ф. Шарыгина; Рос. акад. наук, Рос. акад. образования, изд-во «Просвещение». — 10-е изд. — М. : Просвещение, 2008.—302 с.: ил. — (Академический школьный учебник).
Математика, 5—б : кн. для учителя / [С. Б. Суворова, Л. В. Кузнецова, С. С. Минаева, Л. О. Рослова]. — М. : Просвещение, 2006. — 191 с. : ил.
Математика. 6 класс: поурочные планы по учебнику Г. В, Дорофеева, С. Б. Суворовой, И. Ф. Шарыгина и др. Часть II / авт.-сост. Т. Ю. Дюмина. - Волгоград: Учитель, 2006. - 247 с.
Решение задач по статистике, комбинаторике и теории вероятностей. 7—9 классы. / авт.- сост. В. Н. Студенецкая. Изд. 2-е, испр. - Волгоград: Учитель, 2006. -428 с.
Уроки математики с применением информационных технологий. 5-10 классы. Методическое- пособие с электронным приложением / Л.И. Горохова и др. 2-е изд., стереотип. -М.: Издательство «Глобус», 2010. - 266 с. (Coвременная школа).
Преподавание математики в современной школе. Методические рекомендации. Владивосток: Издательство ПИППКРО, 2003.
Автор-составитель - Р.И. Махиня, главный методист ПИППКРО, заслуженный учитель РФ, Рецензенты: Г.К. Пак, кандидат физико-математических наук ДВГУ; Е.А. Ланкина, кандидат физико-математических наук ДВГУ.
http://mmmf.math.msu.su/
http://portfolio.1september.ru/
http://combinatorica.narod.ru/
План урока:
Оргмомент
Проверка домашнего задания
Актуализация знаний
Объяснение нового материала.
Физкультминутка.
Формирование умений и навыков решения задач на сочетания всеми приемлемыми способами.
Итоги урока
Домашнее задание.
Ход урока
1. Оргмомент
2. Проверка дом. задания (фронтально) и сверить ответы с решениями


 (Слайды 2-4)
(Слайды 2-4)
3. Актуализация знаний. Устная работа
 (Слайд 5)
(Слайд 5)
Вызвать к доске 4 учащихся – решение задач по карточкам.
| Карточка № 1. Сколько двузначных чисел можно составить, используя цифры 1, 2, 3, 4? Реши задачу удобным способом. |
| Карточка № 2. Миша решил в воскресенье навестить дедушку, своего друга Петю и старшего брата Володю. В каком порядке он может организовать визиты? Сколько вариантов получилось? Решить с помощью дерева вариантов. |
| Карточка № 3. В одной деревне по сложившейся традиции мужчин называют каким-либо из следующих имен: Иван, Петр, Василий и Михаил. Проживают в этой деревне 15 мужчин. Может ли оказаться так, что в деревне нет мужчин с одинаковым именем и отчеством? Реши задачу, составив таблицу. |
| Карточка № 3. В пятницу в 4 классе должно быть четыре урока: математика, русский язык, физкультура и рисование. Сколько вариантов у завуча школы, который должен составить расписание занятий на пятницу для 4 класса. Реши задачу удобным способом. |
Учащиеся в тетрадях решают самостоятельно решают задачи.
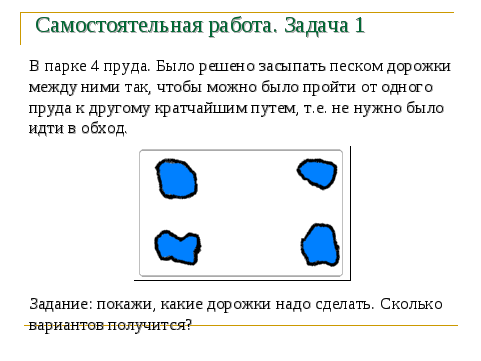

(Слайды 6,7)
Ответы к задачам самостоятельной работы


(Слайды 9,10)
Способ решения первой задачи называется методом графов.
4. Объяснение нового материала
Учитель. Запищите в тетрадь тему урока.
На прошлом уроке вы познакомились с комбинаторными задачами на перестановки. Сегодня мы рассмотрим другой вид задачи. Чтобы понять их особенности, решим две задачи.



(Слайды 12-14)
Таким образом, выбрать двух школьников из четырех можно шестью
способами.(Обратите внимание, что числа расположены в виде треугольника.)
Задача 2 (рассмотреть задачу 2 из школьного учебника).
 (Слайд 16)
(Слайд 16)
Каждый из языков обозначим его первой буквой, и тогда каждый словарь будет «словом» из двух букв: например, АН — это англо-немецкий словарь, а НА — немецко-английский.
Выпишем эти «слова» в алфавитном порядке, причем для удобства подсчета вариантов каждую группу «слов», начинающихся с одной и той же буквы, расположим в отдельной строке.
Сначала фиксируем букву А и добавляем к ней все остальные буквы, кроме, естественно, самой буквы А. Так мы получим первую строку: АН, АР, АФ. Затем фиксируем букву Н и, добавляя к ней остальные буквы, получаем вторую строку и т. д. В результате получим 12 «слов»:
 (Слайд 17)
(Слайд 17)
Таким образом, переводчику понадобится 12 словарей.
Задача № 3.
 (Слайд 18)
(Слайд 18)


(Слайды 19,20)
Учитель: - Что общего в рассмотренных задачах? (В рассмотренных задачах из четырех элементов нужно было выбрать всевозможными способами два.)
- Почему в первой задаче мы получили 6 способов, а во второй 12? (В первой задаче коды 12 и 21 считались одинаковыми, а во второй АН и НА - разными.)
Учитель. Таким образом, в обеих задачах нужно было, как говорят в математике, составить сочетания из четырех элементов по два.
В первой задаче нам был не важен порядок этих сочетаний, то есть выбор двух школьников был равноправен.
А во второй задаче при работе с двумя языками, например русским и английским, нужны два словаря: англо-русский и русско-английский. Поэтому порядок сочетаний был важен, и именно поэтому в результате получилось ровно в два раза больше вариантов.
Вопрос:
- Как можно изменить условие первой задачи, чтобы в результате получилось не 6, а 12 вариантов?
Учитель.


(Слайд 21,22)
 (Слайд 23)
(Слайд 23)
Решаются они с помощью кодирования и подсчета кодов путем расположения их треугольником, с помощью дерева вариантов, таблиц.
Рассмотрим еще одну задачу (задача 3 из учебника).
Задача 3. При встрече 8 приятелей обменялись рукопожатиями. Сколько всего было рукопожатий?
Дадим каждому из приятелей номер — от 1 до 8. Тогда каждое рукопожатие можно закодировать двузначным числом. Например, двузначное число 47 — это рукопожатие между приятелями под номерами 4 и 7.
Ясно, что среди кодов рукопожатий у нас не появится, например, 33 — это означало бы, что один из друзей пожал руку сам себе. Кроме того, такие коды, как, например, числа 68 и 86, означают одно и то же рукопожатие, а значит, учитывать надо только одно из них. Договоримся, что из чисел, кодирующих одно и то же рукопожатие, мы всегда будем учитывать меньшее. Поэтому из чисел 68 и 86 надо выбрать 68.
Коды рукопожатий естественно выписывать в порядке возрастания. Для подсчета их удобно расположить треугольником:
12, 13, 14, 15, 16, 17, 18,
23, 24, 25, 26, 27, 28,
34, 35, 36, 37, 38,
45, 46, 47, 48,
56, 57, 58,
67, 68,
78.
Число кодов равно: 7 + 6 + 5 + 4 + 3 + 2 + 1 = 28. Таким образом, всего было сделано 28 рукопожатий.
Как вы думаете, можно решить эту задачу методом графов или таблицы? (Да)
5. Физкультминутка. (Слайд 24)
6.Формирование знаний и умений.
Решение задач на сочетания из учебника № 868, 869 на доске и в тетрадях. (Слайд 25)
№ 868. Выпишите все возможные двузначные и трехзначные числа, которые можно составить из цифр 0, 1,2, 3, используя каждую цифру в записи только один раз.
Проверка решения задачи:
 (Слайд 26)
(Слайд 26)
869. а) На соревнование по легкой атлетике нужно отправить двух мальчиков из пяти лучших спортсменов среди шестиклассников — Антона, Петра, Бориса, Володи, Коли. Перечислите все варианты выбора участников соревнования. Сколько этих вариантов?
б) Для участия в эстафете 2x100 м нужно выбрать двух мальчиков из пяти, обязательно указав, кто побежит первым, а кто — вторым. Перечислите все варианты выбора участников соревнования в этом случае. Сколько этих вариантов?
Проверка решения задачи:
 (Слайд 27)
(Слайд 27)
№ 870 самостоятельно с проверкой на слайде.
870. На районной олимпиаде по математике оказалось шесть победителей. Однако на областную олимпиаду можно отправить только двоих.
а) Сколько существует вариантов выбора двух кандидатов? Указание. Дайте каждому победителю номер — от 1 до 6.
б) Сколько существует вариантов, если один из шести ребят признан лучшим и он обязательно будет участвовать в областной олимпиаде?
 (Слайд 28)
(Слайд 28)
Самостоятельная работа
Самостоятельно решить в тетрадях следующие задачи. Затем поменяться тетрадью с соседом и взаимообразно проверить решения соседа и оценить.


(Слайд 29,30)
Проверка решения задач:

(Слайд 31,32)
(Слайд 33, 34)
Итоги урока
Вопросы учащимся:
- В чем состоит особенность задач на сочетания?
- Какие два вида таких задач существуют? В чем состоит их отличие?
- Если нужно выбрать всевозможными способами из п элементов т элементов, то в каком случае получится больше вариантов: когда порядок важен или когда порядок не важен? (Слайд 35)
8. Домашнее задание. (Слайд 36)
№ 875, стр.207 № 4. инд.№ 884.
Придумать по 2 задачи сочетание.
Спасибо за урок. (Слайд 37)
11







 (Слайды 2-4)
(Слайды 2-4) (Слайд 5)
(Слайд 5)






 (Слайд 16)
(Слайд 16) (Слайд 17)
(Слайд 17) (Слайд 18)
(Слайд 18)



 (Слайд 23)
(Слайд 23) (Слайд 26)
(Слайд 26) (Слайд 27)
(Слайд 27) (Слайд 28)
(Слайд 28)












