Тема: Решение логарифмических неравенств. Методы отбора корней. Типичные ошибки обучающихся.
Добрый день. Предлагаю рассмотреть способы решения и ошибки в решениях задания профильного уровня математики ЕГЭ этого года №15. Данное здание входит в число тех, к которым учащиеся приступают чаще всего. Поэтому, применяя различные методы решения данного задания мы можем предупредить те ошибки, которые ученики допускают на экзамене и тем самым позволить учащимся быть более успешными. Текст задания вы видите на экране.
Решить неравенство: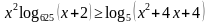
Рассмотрим, как можно было бы решать данное неравенство разными подходами. Заметим, что 625 это 54, следующее, что можно заметить, что выражение 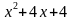 это точный квадрат выражения (х+2)2, следовательно, неравенство может быть записано следующим образом:
это точный квадрат выражения (х+2)2, следовательно, неравенство может быть записано следующим образом:
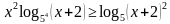
Далее приводим множители в левой и правой части к такому виду, чтобы они стали одинаковыми:
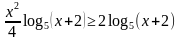
В правой части выносим 2 очень аккуратно, не забываем, что появляется модуль, но за счет того, что выражение (х+2) есть в левой части, используя свойства логарифмической функции модуль опускаем, но не забываем, что х-2. Исходное неравенство мы преобразовали в неравенство вида: 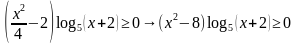 .
.
Далее рассмотрим несколько способов решения данного неравенства.
Способ 1. Левая часть неравенства - это произведение двух множителей, значит есть две возможности, когда оба выражения принимают неотрицательные или неположительные значения.
Первая возможность: 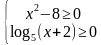 →
→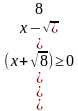 →
→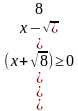


 Отметим все на числовой прямой:
Отметим все на числовой прямой:







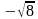
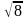
-1
Зафиксируем этот момент: [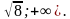
Рассмотрим вторую возможность, когда оба множителя принимают неположительные значения. Аналогично повторим все для 2 случая: 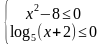 →
→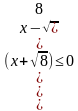 →
→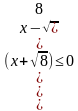











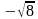
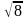
-1
-2
Отметим все на числовой прямой:
Получаем: ( .
.
Объединяем решения и получаем ответ: ( ]
]
Способ 2. (Метод рационализации, композиции, метод замены множителей).
Заметим, что в произведении, стоящем в левой части мы можем заменить логарифм на следующее выражение:  -2)(5-1)(х+2-1)≥0
-2)(5-1)(х+2-1)≥0

 умножаем обе части на 4, получаем
умножаем обе части на 4, получаем  -8)(5-1)(х+2-1)≥0, далее разделим обе части на 4:
-8)(5-1)(х+2-1)≥0, далее разделим обе части на 4:  . Но еще мы должны учитывать, что х-2. Используя метод интервалов, проставляем знаки на числовой прямой
. Но еще мы должны учитывать, что х-2. Используя метод интервалов, проставляем знаки на числовой прямой










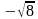
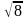
-1
-2
Получаем ответ: ( ]
] .
.
Способ 3. (Классический метод интервалов)
Рассмотрим функцию После введения функции определяем ее область определения Df=(-2 При таком способе явно выписываем область определения.
При таком способе явно выписываем область определения.
Далее решаем уравнение f(x)=0

 =8 x+2=1
=8 x+2=1
 =-
=-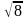 x=-1
x=-1
 =
=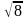
Замечаем, что корень  =- .
=- .
Отмечаем нули функции только на области определения, это важно. На каждом из промежутков находим знаки функции.









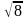
-1
-2
+ - +
Решением неравенства будет объединение промежутков ( ]
] .
.
Способ 4. Он основан на выяснении знака одного из множителей.
У нас есть три варианта:
х+21
х-1



 х2-8≥0
х2-8≥0








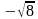
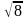
-1
Получаем промежуток  .
.
0
 -2
-2










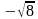
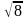
-1


-2
Получаем промежуток ( ).
).
х+2=1
х=-1
Объединяя все решения, получаем ответ: ( ]
] .
.
Далее рассмотрим типичные ошибки, которые допускают ученики при решении данного неравенства
1.Деление обеих частей неравенства на выражение, которое может принимать отрицательное значение.
В неравенстве 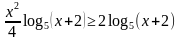 делят обе части неравенства на выражение
делят обе части неравенства на выражение  и получают неравенство
и получают неравенство  , не учитывая, что данное выражение может быть отрицательным.
, не учитывая, что данное выражение может быть отрицательным.
2. Сокращение логарифмов в обеих частях неравенства при том, что в неравенстве остались другие элементы:
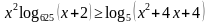
Ошибка от того, что при решении логарифмических неравенств мы учим детей «отбрасывать» логарифмы, забывая о том, что это работает только в том случае, когда в уравнении нет других элементов.
3. Этот случай похож на второй: 
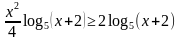
4. Некорректное применение свойств разности логарифмов в случаях, когда при логарифмах стоят коэффициенты:
5. Использование того, что показательная функция возрастает, хотя она может и убывать:

Ученики убирают основания степени забывая, что здесь рассматриваются 2 возможности, идущие от свойств показательной функции.
Спасибо за внимание!







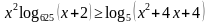
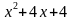 это точный квадрат выражения (х+2)2, следовательно, неравенство может быть записано следующим образом:
это точный квадрат выражения (х+2)2, следовательно, неравенство может быть записано следующим образом: 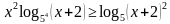

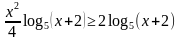
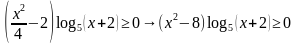 .
.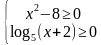 →
→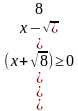 →
→

 Отметим все на числовой прямой:
Отметим все на числовой прямой: 




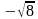
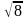
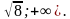
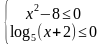 →
→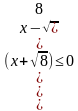 →
→









