Решение олимпиадных задач. Динамическое программирование

решениЕ задач школьного и

муниципального

Этапов В с ОШ

Педагог ДО Шахова Е.А.

ГБОУ ДО города Севастополя ЦДО «Малая академия наук»

Севастополь, 2018

Подготовка участников олимпиад

• выявление;
• привлечение к изучению языков программирования;
• по возможности организация подготовки на уроках или факультативов;
• информационная и

ресурсная поддержка

педагогов.

Что нужно знать?

• язык программирования ВУ (С++, Pascal, Python, Java);
• базовые алгоритмы (алгоритмические структуры, работа с массивами, структуры данных);
• специальные алгоритмы и методы.

Базовые знания и умения

• свойства кратности, делимости чисел;
• обработка последовательностей данных без массивов;
• обработка массивов;
• записи, векторы, списки и т.д.;
• понятие сложности алгоритма.

Специальные алгоритмы

• динамическое программирование;
• длинная арифметика;
• «жадные» алгоритмы;
• решение геометрических задач;
• теория графов;
• рекурсия и перебор;
• комбинаторные задачи;
• структуры данных.

Динамическое программирование

Динамическое программирование  — метод решения задачи путём её разбиения на несколько одинаковых подзадач, рекуррентно связанных между собой.

ЗАДАЧА X n

ЗАДАЧА X n-1

ЗАДАЧА X n-1

1. Рекурсивное решение: function F(n:integer):integer ; begin if (n else F:= F(n - 1) + F(n - 2); end;" width="640"

Рекуррентные соотношения

Последовательность Фибоначчи  F n  задается формулами: 

F 1  = 1,  F 2  = 1,  F n  =  F n  – 1  +  F n  – 2  при  n   1.

Рекурсивное решение:

function F(n:integer):integer ;

begin

if (n

else F:= F(n - 1) + F(n - 2);

end;

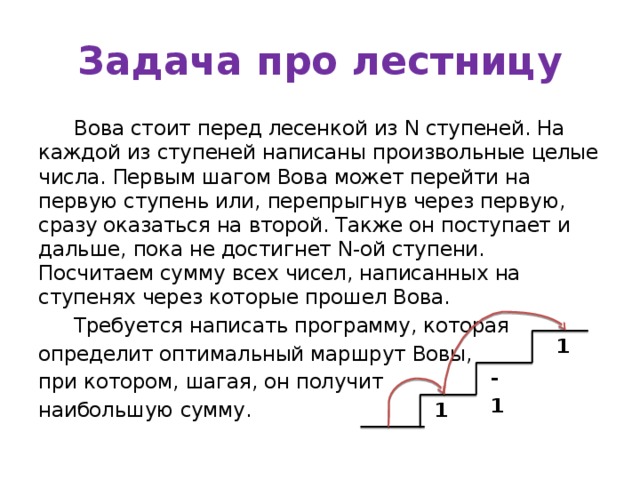
Задача про лестницу

Вова стоит перед лесенкой из N ступеней. На каждой из ступеней написаны произвольные целые числа. Первым шагом Вова может перейти на первую ступень или, перепрыгнув через первую, сразу оказаться на второй. Также он поступает и дальше, пока не достигнет N-ой ступени. Посчитаем сумму всех чисел, написанных на ступенях через которые прошел Вова.

Требуется написать программу, которая

определит оптимальный маршрут Вовы,

при котором, шагая, он получит

наибольшую сумму.

1

-1

1

Математическая модель

Пусть a i – число, написанное на ступеньке № i, а S i – максимальная сумма, которую можно получить, дойдя до i-той ступеньки.

Допустим, нам известны все S i при i

?

S N

S N =max{S N-1 , S N-2 }+ a N

!

S N-1

S 1 = a 1 S 2 = max{0, a 1 }+ a 2

S N-2

Пример решения

i

1

a

2

S

1

3

2

4

-2

5

-3

6

-2

7

4

2

8

1

1

3

1

0

-1

4

6

7

?

Как определить оптимальный путь?

Вариант 1: Запоминать номера ступенек, с которых выгоднее ступать.

Вариант 2: По значениям S вычислить номера ступенек, с которых поднимались, получив данное значение.

!

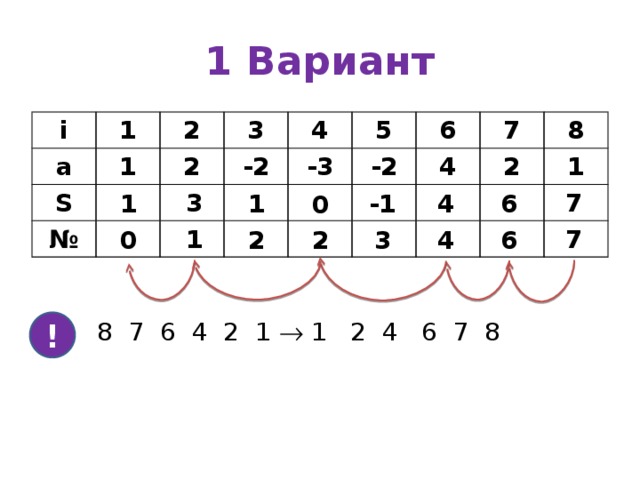
1 Вариант

i

1

a

2

1

S

3

2

№

4

-2

5

-3

6

-2

7

4

2

8

1

3

7

1

7

6

1

4

-1

1

4

6

3

2

0

0

2

8 7 6 4 2 1  1 2 4 6 7 8

!

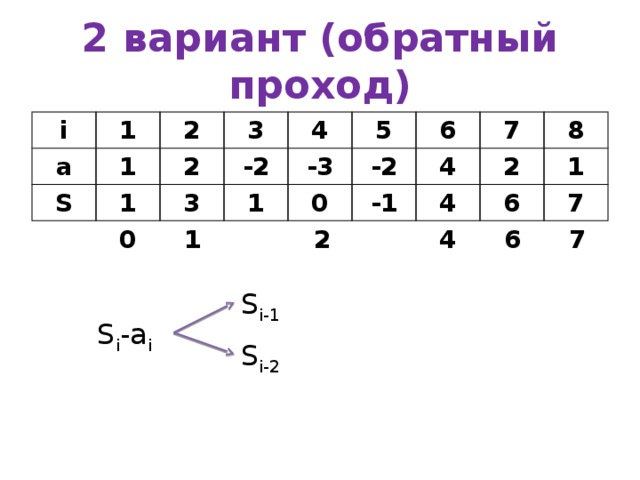
2 вариант (обратный проход)

i

1

a

1

S

2

1

3

2

3

4

-2

5

1

-3

-2

6

0

7

-1

4

2

8

4

6

1

7

0

1

2

4

6

7

S i-1

S i -a i

S i-2

Программная реализация

var N, I, j : integer;

a : array[1..1000] of integer;// числа на ступеньках

S : array[0..1000] of longint; // суммы чисел

k : array[1..1000] of integer; //номера ступенек

Begin

{ввод данных: N и массив a}

{заполнения массива S}

{обратный ход, заполнение массива k}

{вывод результата}

end.

s[i-2] then // определяем максимум s[i]:=a[i]+s[i-1] else s[i]:=a[i]+s[i-2] end;" width="640"

Прямой ход

s[0]:=0; s[1]:=a[1]; // инициализация

for i:=2 to n do

begin

if s[i-1]s[i-2] then // определяем максимум

s[i]:=a[i]+s[i-1]

else

s[i]:=a[i]+s[i-2]

end;

Обратный ход

i:=N; // начинаем с последней ступени,

j:=1; k[1]:=N; // запоминаем ее в массив

while i0 do // пока не спустимся с лестницы

begin

inc(j);

if s[i]-a[i]=s[i-1] then // пришли с (i-1)-й ступени

k[j]:=i-1

else k[j]:=i-2; // пришли с (i-2)-й ступени

i:=k[j]; // переходим на другую ступень

end;

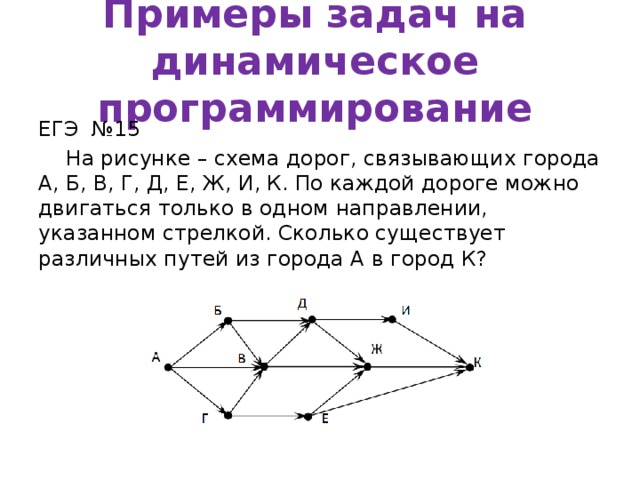
Примеры задач на динамическое программирование

ЕГЭ №15

На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?

Примеры задач на динамическое программирование

ЕГЭ №22

У исполнителя Калькулятор две команды, которым присвоены номера:

• 1. прибавь 1
• 2. умножь на 2

Сколько есть программ, которые число 1 преобразуют в число 16?

Примеры задач на динамическое программирование

При переработке радиоактивных материалов образуются отходы двух видов — особо опасные (тип A) и неопасные (тип B). Для их хранения используются одинаковые контейнеры. После помещения отходов в контейнеры последние укладываются вертикальной стопкой. Стопка считается взрывоопасной, если в ней подряд идет более одного контейнера типа A. Стопка считается безопасной, если она не является взрывоопасной.

Для заданного количества контейнеров N определить количество возможных типов безопасных стопок.

Примеры задач на динамическое программирование

В каждой клетке прямоугольной таблицы N*M записано некоторое число. Изначально игрок находится в левой верхней клетке. За один ход ему разрешается перемещаться в соседнюю клетку либо вправо, либо вниз (влево и вверх перемещаться запрещено). При проходе через клетку с игрока берут столько килограммов еды, какое число записано в этой клетке (еду берут также за первую и последнюю клетки его пути).

Требуется найти минимальный вес еды в килограммах, отдав которую игрок может попасть в правый нижний угол.

Список использованных источников

• Материалы сайта Полякова К.Ю по подготовке к ЕГЭ http://kpolyakov.spb.ru/school/ege.htm.
• Сайт «Школа программирования» - ACMP.ru
• Динамическое программирование для начинающих. - https ://tproger.ru/articles/dynprog-starters /
• Казимиров А., Динамическое программирование. Классические задачи . - https://habr.com/post/113108/