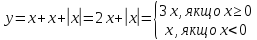Просмотр содержимого документа
«Решение олимпиадных задач по математике»
Побудова графіків функції з модулями.
Задачі на побудову графіків функцій з модулями часто пропонують на математичних олімпіадах для учнів. Ця стаття допоможе вчителеві ознайомити учнів з методами побудови таких графіків. Методичні рекомендації пропонуються у формі коментарів до побудови графіків.
Актуалізація опорних знань:
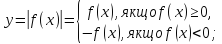
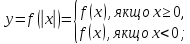
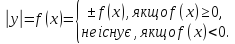
Задачі:
Побудувати графік функції.
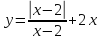
Розв’язання.
Знаходимо область визначення функції: Д(у):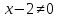
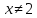
За означенням модуля маємо:
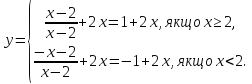
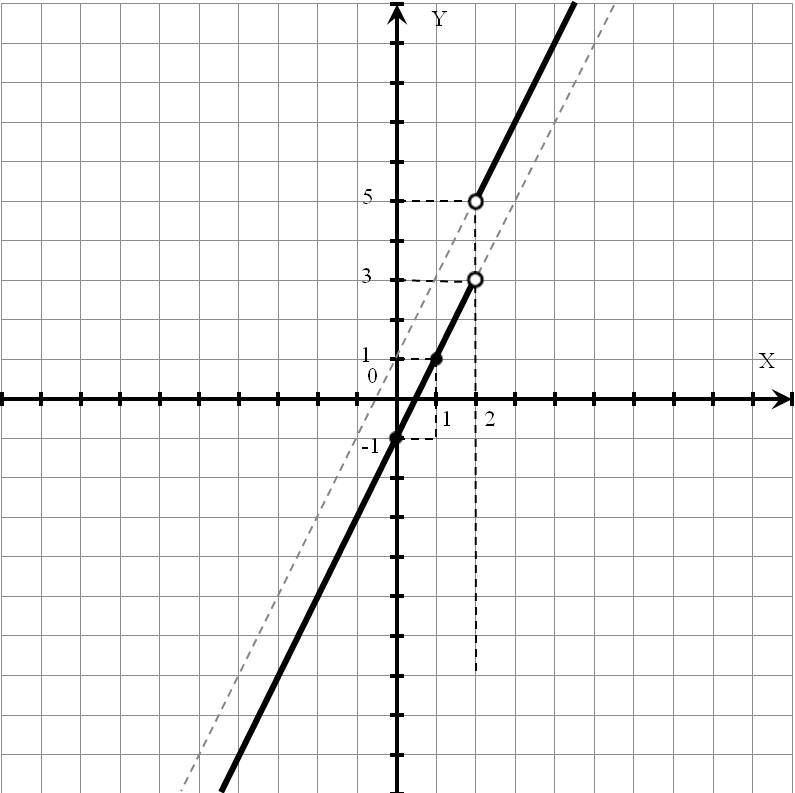 рис.1
рис.1
Виколюємо точку x=2, яка не входить до Д(у).
Відповідь: див. рис.1
Побудувати графік функції.
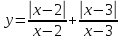
Розв’язання.
Д(у): 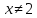
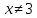
Знаходимо підмодульні корені, розв’язав рівняння
x-2=0 і x-3=0
x=2 і x=3
Наносимо підмодульні корені на числову пряму і отримаємо проміжки




- - + - + + x
2 3
З’ясовуємо знак кожного підмодульного виразу на кожному із отриманих проміжків.
Спрощуємо вираз в кожному отриманому проміжку:
1) 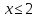
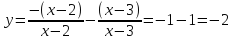
2) 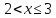
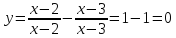
3) 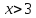
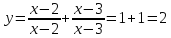
Наносимо підмодульні корені х=2 і х=3 на вісь Ох в системі координат. Прямі х=2 і х=3 проводимо штриховою лінією.
Будуємо отримані графіки на кожному із проміжків. Виколюємо на графіках точки х=2 і х=3.
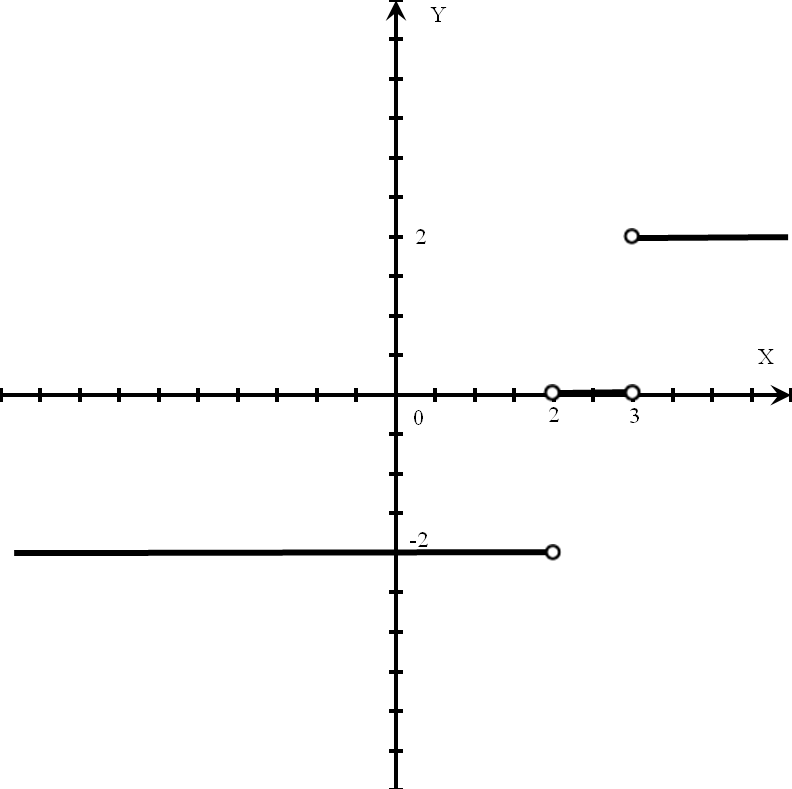 Рис.2
Рис.2
Відповідь: Див. рис.2
Побудувати графік функції
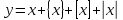
Розв’язання.
Знаючи, що 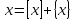 , маємо
, маємо
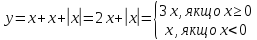
Графік має вигляд:
Рис.3
Відповідь: Див. рис.3
Побудувати графік функції.
 +
+
Розв’язання.
Після тотожних перетворень одержимо:
Д(у):

За вказаною схемою в задачі 2 маємо:




Немає рішень 



 + - + + x
+ - + + x
-1 3
1) 

2) 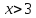

Маємо графік:
рис.4
Відповідь: Див.рис.4
Побудувати графік функції.

Розв’язання.
Д(у):
За означенням модуля маємо:
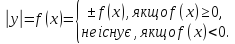
Тому має місце
 і
і  , якщо
, якщо  , тобто
, тобто 
Графік має вигляд
Рис.5
Відповідь: Див. рис.5
Побудувати графік функції.

Розв’язання.
Д(у): ;
; 
За означенням модуля маємо:
Графік має вигляд:
Рис.6
Відповідь: Див. рис.6
7.Побудувати графік функції.

Розв’язання.
Д(у):

За означенням модуля
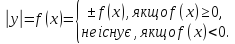
Маємо графіки:
Якщо 

1)

2)

= =


Будуємо графік функції
Рис.7
Відповідь: Див. рис.7







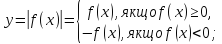
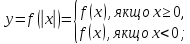
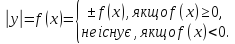
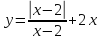
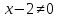
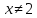
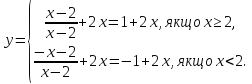
 рис.1
рис.1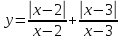
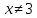



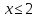
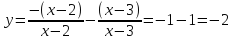
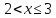
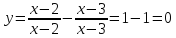
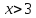
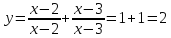
 Рис.2
Рис.2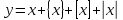
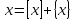 , маємо
, маємо