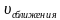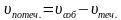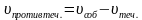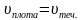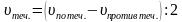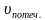Муниципальное образовательное учреждение
«Бендерская средняя общеобразовательная школа №2»
Секция: «Математика»
Исследовательская работа на тему: «Решение текстовых задач на движение (подготовка к ЕГЭ)»
Выполнила: Белоус Юлиана
Ученица 10-А класса
Руководитель: Белоус Татьяна Васильевна
2 квалификационная категория
Содержание
Введение 3
Краткая аннотация 3
1. Основная часть. Текстовые задачи. 4
1.1 Немного истории. 4
1.2 Задачи на движение. 5
2. Классификация задач на движение. 6
2.1 Задачи на движение по прямой 11
2.2 Задачи на движение по окружности (замкнутой трассе) 13
2.3 Задачи на движение по воде 14
2.4 Задачи на среднюю скорость 15
2.5 Прямолинейное движение не по одной прямой. Движение в гору и с горы. 16
2.6 Задачи на движение протяженных тел. 16
Заключение 17
Источники: 18
Введение
Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их (Д.Пойа)
Актуальность выбранной темы вызвана тем, что на итоговой аттестации по математике в 9 и 11 классах есть задачи на движение. Мне необходима эта тема, потому что через год надо сдавать экзамен по математике (ЕГЭ). В своей работе я рассматриваю виды задач га движение и способы их решения.
Краткая аннотация
В работе рассматривается классификация решения задач на движение. Решение задач на движение-важная составляющая курса математики. Умение решать задачи является одним из основных показателей уровня математического развития школьника. Математическая задача неизменно помогает нам выработать правильные математические понятия, глубже выяснить различные стороны взаимосвязей в окружающей нас жизни, дает возможность применять изучаемые теоретические положения.
Предметом исследования моей работы являются задачи на движение. Я разобью свои задачи на группы и попробую сформулировать способ решения каждой из группы.
Целью исследовательской работы является:
Задачи работы:
-
Изучить теоретические сведения по теме «Виды задач на движение».
-
Систематизировать задачи на движение по видам.
-
Провести анкетирование среди учащихся нашей школы.
-
Подобрать задачи; чтоб привести примеры задач и примеры решения задач разных видов.
-
Научиться анализировать и решать задачи на движение.
-
Тренировать вычислительные навыки.
-
Создать памятку: «Как решать задачи на движение».
Гипотеза: При грамотном использовании компьютера можно повысить интерес к решению задач по теме движение.
Мною разобраны и решены ___ задач, которые представлены в тексте. При работе я использовала Интернет-ресурсы, книги и журналы, которые используются при подготовке к экзаменам и урокам математики.
В своей работе я пользовалась следующими методами исследования: опрос, поиск информации, наблюдение, измерение, анализ, обобщение.
Опросив учителей и учащихся нашей школы, я выяснила, что наибольшую трудность у учащихся вызывают задачи на движение.
Анализ данных диаграммы позволил сформулировать проблему: многие ученики не умеют решать задачи на движение.
1. Основная часть. Текстовые задачи.
В окружающей нас жизни возникает множество таких жизненных ситуаций, которые связаны с числами и требуют выполнения арифметических действий над ними-это задачи. Решать задачи нас учат на уроках математики, начиная с первого класса. Но несмотря на это, многие ученики испытывают трудности при решении задач.
Ещё в начальной школе мы познакомились с задачами на движение. Я знаю, что в задачах на движение рассматриваются три взаимосвязанных величины: расстояние (пройденный путь), время движения и скорость-расстояние, пройденное за единицу времени.
Но я не задумывалась, что задачи на движение можно разделить на виды. А по виду задачи можно выбрать её решение. То есть у меня не было четкой системы.
1.1 Немного истории.
Сюжетные задачи-это наиболее древний вид задач. Во всех сохранившихся письменных памятниках древности встречаются разные сюжетные задачиm в том числе и задачи на движение.
Например, во 2 веке в Китае решали следующую задачу:
Задачи из учебника Л.Ф.Магницкого: Послан человек из Москвы на Вологду, и велено ему в хождении своем совершати на всякий день 40 верст; потом другой человек в другий (следующий) день послан в след его и велено ему идти на день 45 верст, и ведательно есть, в коликий день постигнет (догонит) второй первого.
Приведем пример старинной русской задачи.
Из Москвы в Тверь вышли одновременно два поезда. Первый проходил в час 39 вёрст и прибыл в Тверь двумя часами раньше второго, который проходил в час 26 вёрст. Сколько верст от Москвы до Твери?
Как видно, две последние задачи относятся к типу задач на движение. Это лишний раз подтверждает тот факт, что подобным задачам придавали особое значение во все времена.
1.2 Задачи на движение.
Задачи на движение имеют важное практическое значение: это единственный вид учебных задач, в процессе решения которых учащимся необходимо использовать сразу несколько различных информационных и математических моделей: графические (чертёж, схема, граф), реляционные (таблица) и алгебраические (алгебраические выражения, уравнения, неравенства, системы уравнений и неравенств). Графическая модель позволяет лучше понять взаимосвязи и отношения, описанные в условии задачи, табличная модель-определить наиболее удобный способ решения, математическая модель стоится с целью получения ответа на поставленный вопрос.
Одной из особенностей задач на движение является то, что всякая такая задача требует обязательного анализа. Без предварительного анализа трудного определить, какой метод, и какая соответствующая математическая модель являются наиболее подходящими для решения данной задачи. Процессы реальной жизни характеризуются величинами, между которыми существуют определенные зависимости.
Этапы решения задач
-
Анализ содержания задачи.
-
Поиск пути решения задачи и составление плана её решения.
-
Осуществление плана решения задачи.
-
Проверка решения задачи.
Стандартная схема решения таких задач включает в себя:
-
Выбор обозначения неизвестных.
-
Составление уравнений (возможно неравенств) с использованием неизвестных и всех условий задачи.
-
Решение полученных уравнений (неравенств).
-
Отбор решений по смыслу задачи.
При решении этих задач принимают следующие допущения:
-
Если нет специальных оговорок, то движение считают равномерны.
-
Скорость считается величиной положительной.
-
Всякие переходы на новый режим движения на новое направление движения считают происходящими мгновенно.
-
В задачах на движение используются обычно формулы, выражающие законы равномерного движения 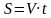 , где
, где 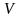 -Скорость равномерного движения
-Скорость равномерного движения
S-пройденное расстояние, t-время движения.
-
При составлении уравнений в таких задачах часто бывает удобно прибегнуть к геометрической иллюстрации процесса движения: путь изображается в виде отрезка прямой, место встречи движущихся с разных сторон объектов точкой (флажком) и т.д.
-
Часто для усложнения задачи её условие формулируется в различных единицах измерения (метры, километры, часы, минуты и т.д.). В этом случае необходимо пересчитывать все данные задачи в одинаковых единицах измерения.
2. Классификация задач на движение.
В основу нашей классификации была положена классификация текстовых задач на движение Пасечник Л.А. и Беловой Е.И. учителей математики. Учитель математики Белова Е.И. рассматривает типы классификаций задач на движение, наиболее часто применяемые в курсе математики 5-6 классов. Проанализировав классификацию, которую предлагает Пасечник ЛЮАЮ следует заметить, что её можно расширить… Тем самым, считаю целесообразным, объединить эти классификации и добавить к ней тип задач на движение по замкнутой траектории, часто встречающийся в заданиях ЕГЭ. А также заменить «классификацию на воде», классификацией задачи на движение в разных средах». С учётом выше изложенного предлагаю следующую классификацию:
-
По количеству движущихся объектов;
а) Задачи на движение одного человека, одного велосипедиста, одной машины и т.д.
Задача
Из пункта А в пункт В, расстояние между которыми 80 км, выехал автобус. В середине пути он был задержан на 10 минут, но увеличив скорость на 20 км/ч, прибыл в пункт В вовремя. С какой скоростью автобус проехал первую половину пути?
б) Движение в котором два и более участника.
Задача
Два велосипедиста одновременно отправились в 88-километроывй пробег. Первый ехал со скоростью на 3 км/ч большей, чем скорость второго, и прибыл к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
-
По направлению движущихся объектов;
а) Противоположно направленное движение:
- движение навстречу друг друга;
Задача
Два охотника вышли навстречу друг другу из леса с двух сторон поляны и оказались на расстоянии 450 м друг от друга. Один шёл со скоростью 70 м/мин, другой- со скоростью 80 м/мин. Собака одного из них побежала навстречу другому. Добежав до него, она вернулась к хозяину и, повернув, снова бросилась к его другу. Так она продолжала свой бег до встречи двух охотников. Найти расстояние, которое пробежала собака, если её скорость равна 12 км/ч.
-Движение в разные стороны;
Задача
Из одного пункта одновременно в противоположных направлениях вышли два пешехода. Скорость одного из них 5 км/ч, другого 6 км/ч. Какое расстояние между ними будет через 3 часа?
б) Движение в одном направлении-однонаправленное движение;
Задача
Первый турист, проехав 1,5 часа на велосипеде со скоростью 16 км/ч, делает остановку на 1,5 ч, а затем продолжает путь с первоначальной скоростью. Четыре часа спустя после отправки в дорогу первого туриста вдогонку ему выезжает на мотоцикле второй турист со скоростью 56 км/ч. Какое расстояние они проедут, прежде чем второй турист догонит первого?
-
По времени начала движения;
а) Одновременное движение
Задача
Одновременно из одного пункта в противоположных направлениях вышли два пешехода. Один из них шёл со скоростью 6 км/ч. Через 3 часа пешеходы удалились друг от друга на 30 км. Определите скорость другого пешехода.
б) Разновременное движение.
Задача
Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 10 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час после этого-третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч.
-
По характеру движения;
а) Движение из одного пункта в другой с остановкой в пути;
Задача
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 240 км. На следующий день он отправился обратно в А со скоростью на 1 км/ч больше прежней. По дороге он сделал остановку на 1 час. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А.
б) Движение с возвращением в начальный пункт отправления.
Задача
Машина выезжает из А в В, доехав до В, тут же возвращается обратно. Через 1 час после выезда из А машина была на расстоянии 80 км от В, а ещё через 3 часа-80 км от А. Известно, что весь путь туда и обратно машина прошла менее чем за 9 часов. Найти расстояние от А до В.
-
В зависимости от траектории движения.
а) Прямолинейное движение (движение по прямой, движение автомобиля по ровной дороге без поворотов);
Задача
Два велосипедиста одновременно отправились в 108-километровый пробег. Первый ехал со скоростью на 3 км/ч большей, чем скорость второго, и прибыл к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым.
б) Движение по замкнутой траектории ( по стадиону, по окружности, движение автомобиля на повороте);
Задача
Из пункта А круговой трассы выехал велосипедист, а через 30 минут следом за них отправился мотоциклист. Через 10 минут после отправления он догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км.
-
В зависимости от среды, в которой движутся объекты:
а) задача на движение по водному пути;
-движение по реке; (по течению)
-движение против течения.
Задача
Теплоход проходит по течению реки до пункта назначения 399 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 20 км/ч, стоянка длится 2 часа, а в пункт отправления теплоход возвращается через 42 часа после отплытия из него.
-движение в стоячей воде.
Задача
Лодка шла из пункта А в пункт В по течению за 30 минут, затем из пункта В в пункт А против течения 70 минут. Найти время движения лодки из А в В в стоячей воде.
б) Задачи на движение по воздушному пути;
Задача
Бабочка капустница пролетела 4 с со скоростью 4 м/с, а когда подул попутный ветер скорость бабочки увеличилась на 6 м/с, и она пролетела ещё какое-то количество метров. Какое расстояние пролетела бабочка при попутном ветре, если всего она пролетела 688 м?
в) Задачи на движение в смешанной среде:
Задача
Моторная лодка шла 0,4 ч по озеру и 0,3 ч по течению реки, скорость течения которой 2 км/ч. Всего моторная лодка прошла 9 км. Найдите её собственную скорость.
-
Движение протяженных тел.
Задача
Поезд, двигаясь равномерно со скоростью 60 км/ч проезжает мимо лесополосы, длина которой равна 400 метрам, ща 1 минуту. Найдите длину поезда в метрах.
-
Нахождение средней скорости
Задача
Автомобиль двигался 3,2 ч по шоссе со скоростью 90 км/ч, затем 1,5 ч со скоростью 45 км/ч и наконец 0,3 по просёлочной дороге со скоростью 30 км/ч. Какова средняя скорость автомобиля?
По мнению Бантовой М.А. [] работа над задачами не должна сводится к натаскиванию на решение задач одного вида, затем другого и т.д. Главная цель-научить осознанию устанавливать определённые связи между данными и искомым в разных жизненных ситуациях, предусматривая постепенное их усложнение. Чтобы добиться этого, нужно предусмотреть в методике обучения решению задач каждого вида такие ступени:
-
Подготовительную работу к пониманию задачи (составление схемы, чертежа);
-
Ознакомление с решением задач данного вида;
-
Закрепление умения решать задачи, т.е. тренировка.
Известный отечественный психолог А.Н. Леонтьев писал: «Актуально сознаётся только то содержание, которое является предметом целенаправленной активности субъекта». Поэтому, чтобы структура задачи стала предметом анализа и изучения, необходимо отделить её от всего несущественного и представить её в таком виде, который обеспечивал бы необходимые деёствия. Сделать это можно путем особых знаково-символических средств-моделей, однозначно отображающих структуру задачи и достаточно простых для восприятия школьниками.
В структуре лютой задачи выделяют:
-
Предметную область, т.е. объекты, о которых идёт речь в задаче.
-
Отношения, которые связывают объекты предметной области.
-
Требования задачи.
Решая свою последнюю поставленную в работе задачу, при создании памятки я учитывала мнение Бантовой М.А. и Леонтьева А.Н.
2.1 Задачи на движение по прямой
а) Задачи на встречное движение
При решении задач на встречное движение существенной характеристикой является скорость сближения движущихся объектов. Расстояние, на которое сближаются движущиеся объекты за единицу времени, называют скоростью сближения. При встречном движении скорость сближения равна сумме скоростей движущихся объектов, т.е. 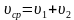
Рисунок №1
Задача.
Расстояние между пунктом А и В 3450 км. Два поезда из этих пунктов вышли навстречу друг другу в одно время и встретились через 24 часа. Найдите скорость второго поезда, если первый поезд за 3 часа проходил 240 км. [ ]
Рисунок №2
Решение.
Пусть x км/ч-скорость второго поезда. По условию между ними 3450 км. И встретятся они через 24 часа. Найдём скорость первого поезда и составим уравнение.
-
240:3=80 (км/ч)-скорость первого поезда.
-
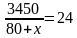
3450=24·(80+x)
3450=1920+24x
1530=24x
X=63,75-V2 поезда
Ответ: 63,75 км/ч.
б) Задачи на движение в одном направлении (движение вдогонку или движение с отставанием)
Рисунок №3
Два объекта движения начинают одновременно в одном направлении, но первый объект обгоняет, другой отстает или первый объект отстает, другой обгоняет. В задачах на движение в одном направлении при одновременном начале движения объектов полезно использовать понятия «скорость удаления» и «скорость сближения»
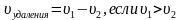
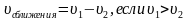
Скорость сближения и скорость удаления находятся вычитанием меньшей скорости из большей.
Задача.
Одновременно два мальчика выехали за город, один на мопеде, другой на скутере, через 1,5 ч расстояние между ними было 20 км. С какой скоростью двигался мальчик на мопеде, если мальчик на скутере двигался 30 км/ч?
Решение:
Рисунок №4 (+таблица)
В) Задачи на движение в противоположных направлениях.
При решении задач такого типа суммарная скорость имеет другое название. Расстояние, на которое удаляются движущиеся предметы за единицу времени, называют скоростью удаления. При движении в противоположных направлениях скорость удаления равна сумме скоростей движущихся объектов, т.е. 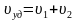
Рисунок №5+ Рисунок №6
Задача.
С одного стадиона одновременно в противоположных направлениях выбежало два спортсмена. Скорость одного их них 20 км/ч, а другого-23 км/ч. На каком расстоянии друг от друга будут спортсмены через час?
Рисунок №7
Решение:
-
20+23=43(км/ч)-скорость удаления спортсменов, это же и будет расстоянием через час.
Ответ:43 км.
2.2 Задачи на движение по окружности (замкнутой трассе)
а) Если два объекта одновременно начинают движение по окружности в одну сторону со скоростями 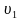 и
и 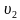 соответственно (
соответственно (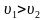 соответственно) то 1 объект приближается ко 2 объекту со скоростью
соответственно) то 1 объект приближается ко 2 объекту со скоростью 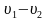 . В момент, когда 1-й объект в первый раз догоняет второго, он проходит расстояние на один круг больше. В момент, когда 1-й объект во второй раз догоняет 2-го, он проходит расстояние на два круга больше и т.д.
. В момент, когда 1-й объект в первый раз догоняет второго, он проходит расстояние на один круг больше. В момент, когда 1-й объект во второй раз догоняет 2-го, он проходит расстояние на два круга больше и т.д.
Задача.
Из пункта А круговой трассы, длина которой равна 30 км, одновременно в одном направлении стартовали два автомобилиста. Скорость первого равна 92 км/ч, скорость второго-77 км/ч. Через сколько минут первый автомобилист будет опережать второго ровно на 1 круг?
Решение
1)92-77=15 (км/ч)-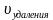
2) 30:15=2 (ч)
2 часа=12- минут.
Ответ: через 120 минут.
б) Если два объекта одновременно начинают движение по окружности из двух диаметрально противоположных точек круговой трассы со скоростями (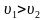 соответственно), то 1-й объект приближается со скоростью
соответственно), то 1-й объект приближается со скоростью 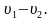 В момент , когда 1-й объект в первый раз догоняет второго, он проходит расстояние на половину круга больше.
В момент , когда 1-й объект в первый раз догоняет второго, он проходит расстояние на половину круга больше.
в) Если из одной точки круговой трассы два объекта одновременно начинают движение в противоположные стороны со скоростями 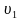 и
и 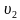 соответственно, t-время до их встречи, то (
соответственно, t-время до их встречи, то (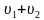 )·t=c, где с-длина круговой трассы.
)·t=c, где с-длина круговой трассы.
Рисунок №1
Задача
Из одной точки круговой трассы одновременно в противоположных направлениях выехали два автомобиля. Найдите длину круговой трассы, если автомобили встретились через 2 часа, скорость первого автомобиля 80 км/ч, скорость второго-100 км/ч.
Решение:
-
100+80=180 (км/ч)-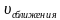
-
180·2=360 (км)- длина трассы
Ответ: 360 км.
2.3 Задачи на движение по воде
-
В задачах на движение по воде скорость течения считается неизменной
-
При движении по течению скорость прибавляется к скорости плывущего тела.
-
При движении против течения-вычитается из скорости тела.
-
Скорость плота считается равной скорости течения.

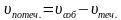
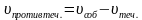

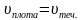
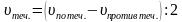
Задача
Катер, имеющий собственную скорость 15 км/ч, плыл 2 ч по течению реки и 3 ч против течения. Какое расстояние он проплыл за всё время, если скорость течения реки 2 км/ч? Какое расстояние пройдёт плот за это время?
Решение
-
15+2=17 (км/ч)- 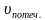
-
17·2=34 (км)- путь катера по течен.
-
15-2=13 (км/ч)- 
-
13·3=39 (км)-путь катера против течения.
-
39+34=73 (км)- весь путь катера
-
3+2=5 (ч)- время движения плота
-
5·2=10 (км)-путь плота
Ответ: 73 км; 10км.
2.4 Задачи на среднюю скорость
Средняя скорость вычисляется по формуле  , где S-путь пройденный телом, t-время, за которое этот путь пройден.
, где S-путь пройденный телом, t-время, за которое этот путь пройден.
Если путь состоит из нескольких участков, то следует вычислить всю длину пути и всё время движения.
Например, если путь состоит из двух участков протяженностью  , скорости на которых были равны соответственно
, скорости на которых были равны соответственно 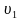 и
и 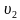 , то:
, то:
-

-

-

-

-

-

-
Задача
Пешеход шёл по дороге 2 часа со скоростью 6 км/ч, по болоту 3 часа со скоростью 2 км/ч, и по полю 1 час со скоростью 6 км/ч. Найдите среднюю скорость пешехода.
Решение:
-
6·2=12 (км)- расстояние, пройденное по дороге.
-
2·3=6 (км)- расстояние, пройденное по болоту.
-
6·1=6 (км)- расстояние, пройденное по полю.
-
2+3+1=6 (ч) общее время.
-
12+6+6=24 (км)-весь путь.
-
24:6=4 (км/ч)-средняя скорость.
Ответ: 4 км/ч.
Запомним, что средняя скорость не равна среднему арифметическому скоростей.
2.5 Прямолинейное движение не по одной прямой. Движение в гору и с горы.
С учетом движения туда и обратно движущийся объект за все время движения проходит:
В гору весь путь, с горы весь путь.
Рисунок №1
Задача
Путь от пансионата до почты, который сначала идёт в гору, а потом под гору, пешеход прошёл за 1 час 40 минут, а обратный путь-за 2 часа 20 минут. В гору он шел со скоростью 3 км/ч, а под гору-со скоростью 6 км/ч. Найдите расстояние от пансионата до почты.
Решение
Весь путь-x
t- на путь в гору= 
t- на путь c горы= 


X=8
Ответ: 8 км.
2.6 Задачи на движение протяженных тел.
В задачах такого типа требуется, как правило, определить длину одного из них. Наиболее типичная ситуаций: определение длины поезда, проезжающего мимо столба или протяженной платформы. В первом случае поезд проходит мимо столба расстояние, равное длине проезда, во втором случае-расстояние, равное сумме длин поезда и платформы.
Задача
Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо придорожного столба за 30 секунд. Найдите длину поезда в метрах.
Решение.
-
30 сек=1/2 мин.=
-
60·  =
=  (км)
(км)
-
 км=500 (м)
км=500 (м)
Ответ: 500 м.
Задача
Поезд длинной 200 м прошёл мимо неподвижного наблюдателя за 30 сек. За сколько времени он проедет тоннель длиной 200 м?
Решение
-
200·0,5=100 (м/мин)- 
-
100+200=300 (м)-длина тоннеля+поезда
-
300:100=3 (мин)
Ответ: 3 мин.
Заключение
Текстовые задачи являются традиционным разделом на выпускных и вступительных экзаменах. Как правило, основная трудность при решении текстовой задачи состоит в переводе её условий на математический язык уравнений. Общего способа такого перевода не существует. Однако многие задачи на экзаменах достаточно типичны. Благодаря проделанной работе я глубже разобралась в теме: «Задачи на движение». В ходе работы я решила 50 задач по исследуемой теме.
-
Проанализировала тексты задач на движение, предложенные в школьных учебниках и материалах ГИА и ЕГЭ.
-
Систематизировала задачи по типам.
-
По каждому типу задач подготовила схемы и выделила подсказки к решению в виде формул и алгоритмов.
-
Подготовила примеры и решения задач разных типов, а также комбинированных задач.
-
К каждой задаче подготовила интерактивные модели.
-
В программе «Power Point» сделала электронный справочник по выбранной теме.
Кроме того, я придумала яркое наглядное пособие, с помощью которого попробую помочь моим сверстникам разобраться в теме «Задачи на движение».
Можно сказать, что благодаря своей исследовательской работе я стала настоящим экспертом в решении задач на движение.
Цели, поставленные в начале исследования, успешно достигнуты.
Источники:
-
В.К. Совайленко. Система обучения математике в 5-6 классах; Москва; «Просвещение»; 1991.
-
А.В. Шевкин. Обучение решению текстовых задач в 5-6 классах; Москва; «Русское слово»; 2002.
-
М.Н. Кочагина, В.В. Кочагин. ГИА 2009. Математика: сборник заданий; Москва 2009.
-
Л.В. Кузнецова и др. Алгебра: сборник заданий для подготовки к гос.итоговой аттестации в 9 классе; Москва; «Просвещение».
-
СА.Шестаков, Д.Д.Гущин ЕГЭ 2010 Математика. Задачи В12. Рабочая тетрадь; Москва; издательство МЦНМО 2010
-
В.А.Поспелов. Задачи на движение. Санкт-Петербург; изд.дом. Литература; 2008
-
Г.В. Дорофеев, Л.Г.Петерсон, Математика. Учебник 5 класс.
-
Н.Я. Виленкин, В.И.Жохов, и др. Математика., учебник 5 класс.
-
Интернет ресурс: www.animan.ru
-
Интернет ресурс: www.zadachi.ru
13






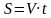 , где
, где 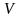 -Скорость равномерного движения
-Скорость равномерного движения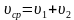
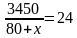
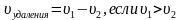
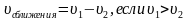
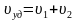
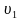 и
и 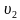 соответственно (
соответственно (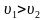 соответственно) то 1 объект приближается ко 2 объекту со скоростью
соответственно) то 1 объект приближается ко 2 объекту со скоростью 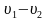 . В момент, когда 1-й объект в первый раз догоняет второго, он проходит расстояние на один круг больше. В момент, когда 1-й объект во второй раз догоняет 2-го, он проходит расстояние на два круга больше и т.д.
. В момент, когда 1-й объект в первый раз догоняет второго, он проходит расстояние на один круг больше. В момент, когда 1-й объект во второй раз догоняет 2-го, он проходит расстояние на два круга больше и т.д.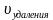
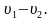 В момент , когда 1-й объект в первый раз догоняет второго, он проходит расстояние на половину круга больше.
В момент , когда 1-й объект в первый раз догоняет второго, он проходит расстояние на половину круга больше.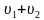 )·t=c, где с-длина круговой трассы.
)·t=c, где с-длина круговой трассы.