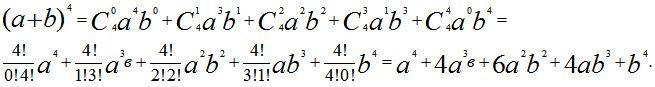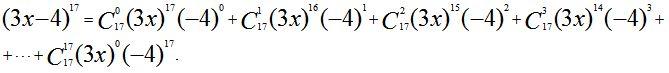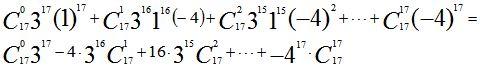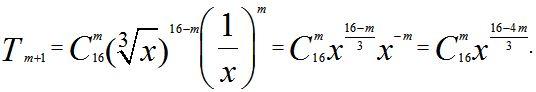Урок № 13 по алгебре и н.м.а в 10 классе 30.09.20г
Учитель Евтушенко М.С.
Общая тема: Рациональные уравнения и неравенства
Тема: Решение упражнений
Тип урока: закрепление изученного материала
Планируемые результаты:
Личностные:
Развивать готовность к самообразованию и решению задач;
Метапредметные:
Учиться критично относиться к своему мнению, с достоинством признавать свои ошибки;
Предметные: научатся самостоятельно находить члены бинома Ньютона.
Формы работы: фронтальная, индивидуальная
Образовательные ресурсы: карточки
ХОД УРОКА
Организационный момент. Проверка домашнего задания.
Постановка цели и задач урока. Мотивация.
3 . Практическая работа .Бином Ньютона
Вопросы к работе
Прочитать формулу бинома Ньютона.
Как строится треугольник Паскаля для нахождения коэффициентов бинома Ньютона?
По какой формуле найти s-й член бинома Ньютона?
Образцы решения заданий
Пример 1. Написать разложение по формуле бинома Ньютона и упростить 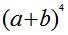 .
.
Решение:
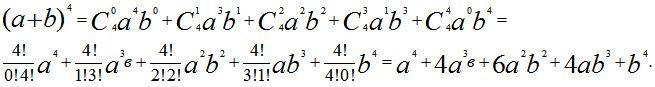
Пример 2. Найти алгебраическую сумму коэффициентов многочлена относительно x, получаемого в разложении бинома Ньютона 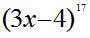 .
.
Решение.
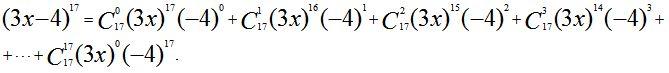
Это равенство истинно при любом значении х.
При x = 1 левая часть равна 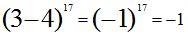 , а в правой части получаем алгебраическую сумму коэффициентов:
, а в правой части получаем алгебраическую сумму коэффициентов: 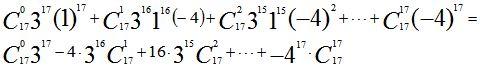
Следовательно, алгебраическая сумма коэффициентов данного многочлена равна –1.
Пример 3. Найти 13-й член разложения бинома
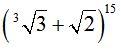 .
.
Решение. Согласно формуле общего члена разложения бинома,
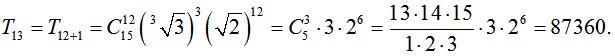
Пример 4. Найти номер члена разложения бинома 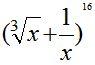 , не содержащего х.
, не содержащего х.
Решение. Для общего члена разложения имеем 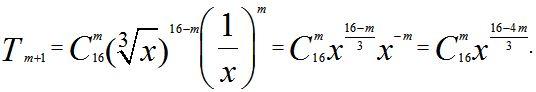
Член разложения не зависит от x; это значит, что показатель степени x равен 0, только тогда, когда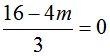 , 16 – 4m = 0, m = 4.
, 16 – 4m = 0, m = 4.
Итак, пятый член данного разложения не зависит от х.
Пример 5. Построить треугольник Паскаля для нахождения
коэффициентов разложения бинома Ньютона 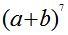 .
.
Решение.
| n | 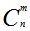 |
| 0 | 1 |
| 1 | 1 1 |
| 2 | 1 2 1 |
| 3 | 1 3 3 1 |
| 4 | 1 4 6 4 1 |
| 5 | 1 5 10 10 5 1 |
| 6 | 1 6 15 20 15 6 1 |
| 7 | 1 7 21 35 35 21 7 1 |
|
| 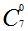 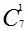 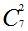 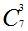 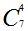 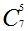 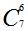 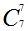 |
Упражнения
Написать разложение по формуле бинома Ньютона и упростить:
а) 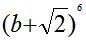 ; Ответ:
; Ответ: 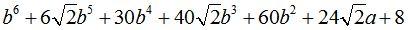 .
.
б) 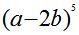 ; Ответ:
; Ответ: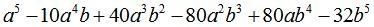 .
.
в) ; Ответ: .
2. Найти пятый и девятый член разложения:
а) , б) . Ответ: .
3. Найти два средних члена разложения . Ответ: .
4. Найти в биномиальном разложении член, не содержащий z. (Ответ:  ).
).
5. Используя треугольник Паскаля найти коэффициенты разложения:
а)  , .
, .
Индивидуальные задания
Разложить по формуле бинома Ньютона и упростить. Коэффициенты разложения найти, используя треугольник Паскаля:
1) ; 2) ; 3) ;
4) ; 5) ; 6) ;
7) ; 8) ; 9) ;
10)
2. Найти два средних члена разложения:
1) ; 2) ; 3) ; 4) ;
Итоги урока. Рефлексия
Домашнее задание: решить № 2.21(а,в)