Решение задач на смеси.

города Магнитогорска

Задачи на смеси ЕГЭ № 11 (2021г.)

Пупкова Т.В., учитель математики МАОУ «Многопрофильный лицей №1»

г. Магнитогорск

Процент

• Процент – сотая доля числа.

1% от числа a?

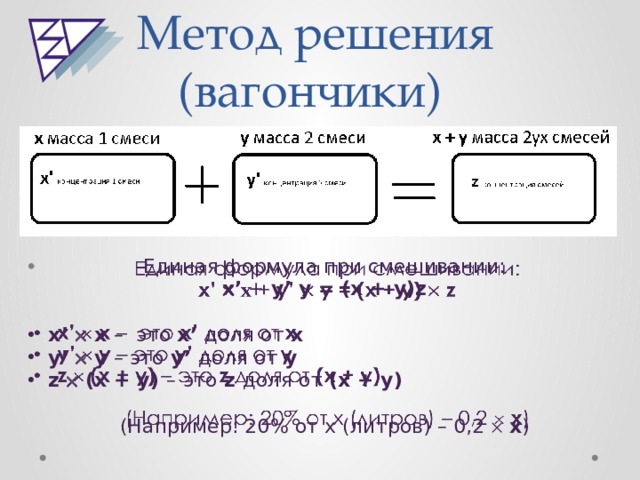
Метод решения (вагончики)

Единая формула при смешивании:

x’ + y’ y = (x + y)z

• x’  x – это x’ доля от x
• y’  y – это y’ доля от y
• z  (x + y) – это z доля от (x + y)

(Например: 20% от x (литров) – 0,2  x )

Задача №1

• Решение:

z = 0,05

Тогда 0,05  100% = 5%

Ответ: 5%

Задача №2

• Смешали некоторое количество 17 процентного раствора некоторого вещества с таким же 19 процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора ?

• Решение:

Тогда 0,18  100% = 18%

Ответ: 18%

Задача №3

• Решение:

Ответ: 190 кг

1 вариант

2 вариант

➀ Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

② Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 6 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?

➀ Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 14 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?

② Имеется два сосуда. Первый содержит 75 кг, а второй - 50 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 42% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 50% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

③ Имеются два сосуда. Первый содержит 30 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

③ Имеется два сплава. Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

Ответы

1 вариант

100

2 вариант

57

133

7,5

18

9