Дата
Тема: РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ «СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА»
Задачи: обобщить теоретические знания учащихся и закрепить навыки решения задач по теме.
Ход урока
-
АКТУАЛИЗАЦИЯ ЗНАНИЙ
Ответьте на вопросы:
- в каком случае существует треугольник с тремя сторонами?
- в любом треугольнике против большей стороны лежит…?
- в любом треугольнике против меньшего угла лежит…?
Выполните устно:
№1
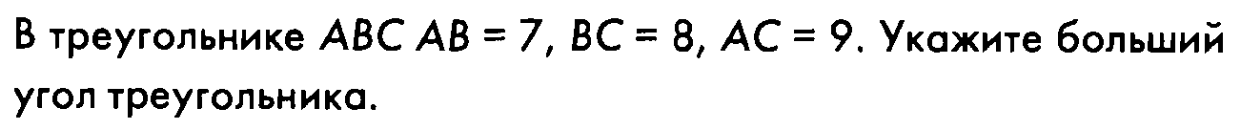
Ответ: (В)
№2
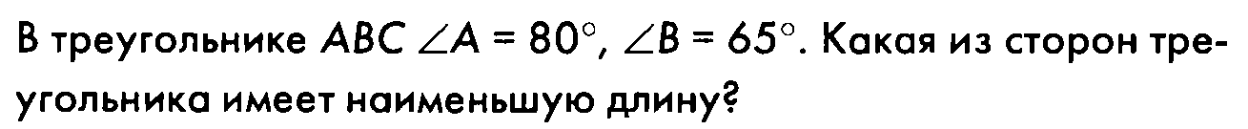
Ответ: (АВ)
№3
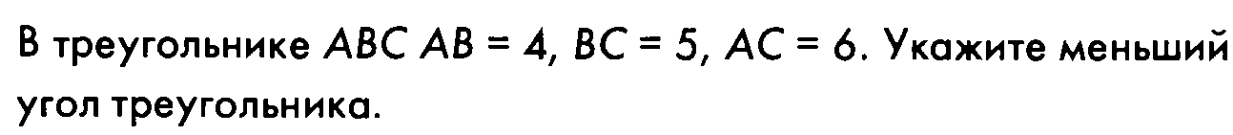
Ответ: (С)
-
ПРАКТИЧЕСКАЯ ЧАСТЬ
Открываем тетради и записываем сегодняшнее число и тему урока. Скоро контрольная работа, так что начинаем повторять пройденный материал. Выполняем письменно приведенные задания.
Задача №1. В равнобедренном треугольнике одна из сторон равна 13, а другая 26. Найти основание треугольника.
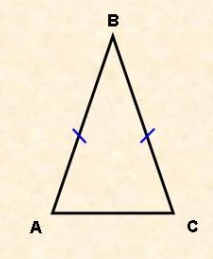
Дано: АВС – равнобедренный треугольник, стороны 13 и 26.
Найти: основание.
Решение. Так как конкретно не сказано по условию задачи, какие из сторон равны 13 и 26, то решение разобьется на 2 случая. И в каждом из случаев нам необходимо будет проверять неравенство треугольников.
1 случай. Пусть АВ=ВС=13, тогда АС=26. Проверим неравенство треугольников и посмотрим, может ли существовать треугольник с такими сторонами.
Должно выполняться: каждая из сторон меньше суммы двух других.
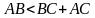
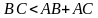
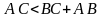
Подставим наши числа:
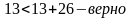
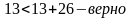
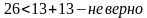
Так как идет нарушение в последнем неравенстве, значит треугольника с такими сторонами не существует.
2 случай. Пусть АВ=ВС=26, тогда АС=13. Проверим неравенство треугольников и посмотрим, может ли существовать треугольник с такими сторонами.
Подставим наши числа:
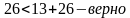
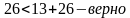
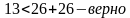
Все неравенства выполняются, значит треугольник с такими сторонами существует.
Ответ: основание равно 13.
Задача №2. Углы треугольника относятся как 1:6:8. Найдите угол А, если сторона ВС наименьшая.
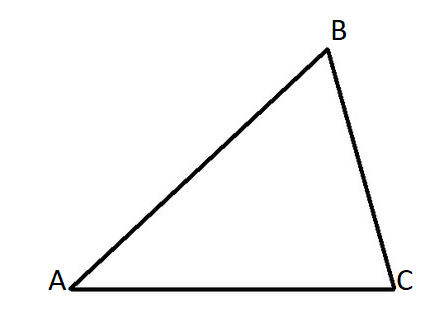
Дано: треугольник АВС, ВС – наименьшая, А:В:С=1:6:8.
Найти: А
Решение. По условию сказано, что сторона ВС – наименьшая. Это значит, что угол, лежащий против этой стороны, так же наименьший. Значит на угол А приходится 1 часть отношения. Введем переменную х – 1 часть отношения. Тогда угол А=х, угол В=6х, угол С=8х. Вспоминаем, что сумма углов любого треугольника равна 180°. Составим и решим уравнение:
х+6х+8х=180°
15х=180°
х=180°:15
х=12°.
Ответ: угол А=12°.
Задача №3. Расстояние от точки А до прямой а на 2 см меньше, чем длина наклонной, проведенной из этой же точки, а их сумма равна 18 см. Найти расстояние от точки А до прямой а.
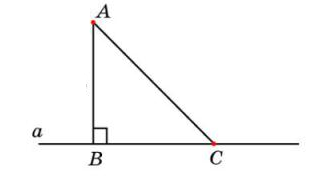
Дано: АВ
Найти: АВ.
Решение. По условию известно, что АВ меньше на 2 см, чем АС. Значит, наоборот АС на 2 см больше, чем АВ. Введем переменную х. Пусть АВ=х, тогда АС=х+2. Известна их сумма АВ+АС=18 см. Составим и решим уравнение:
х+(х+2)=18,
2х+2=18,
2х=16,
х=8 см.
За х мы обозначали АВ, значит АВ=8 см.
Ответ: 8 см.
-
ПОДВЕДЕНИЕ ИТОГОВ УРОКА. РЕФЛЕКСИЯ
Домашнее задание:
Задача №1. Углы треугольника относятся как 3:4:5. Найдите угол В, если сторона АС наибольшая.
(Подсказка: тут угол В лежит против большей стороны, значит на него приходится самая большая часть из отношения углов. Решение подобно задаче №2 из практической части)
Задача №2. Перпендикуляр, опущенный из точки М на прямую а, на 8 см меньше, чем длина наклонной, проведенной из этой же точки, а их сумма равна 18 см. Найти длину перпендикуляра.
(Решение подобно задаче №3 из практической части)







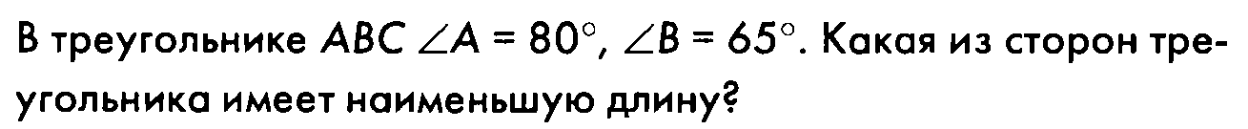
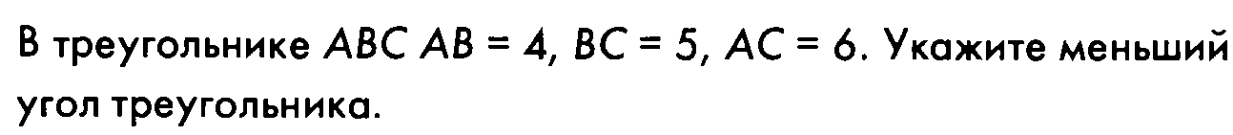

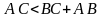
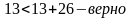
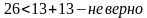
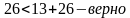
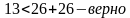










Сложные вопросы обществознания
Русская литература 7 класс ФГОС
Открываем мир вместе
Электронная тетрадь по русскому языку 4...
Русская литература 11 класс ФГОС. Часть...
Решение задач по физике. Механика 7-11...
Электронная тетрадь по химии 8 класс...
Математика 5 класс
© 2020, Живогляд Дарья Владимировна 7605 403
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы