Возможные решения заданий школьного этапа Всероссийской олимпиады по физике за 2023-2024 учебный год.
7 класс
№1
Найдём на рисунке совмещённые риски шкал линейки и термометра. Например, 69 мм соответствует 19 0С, а 60 мм – 13 0С. Расчёт показывает, что на 2 0С приходятся 3 мм. Значит, 5 0С соответствуют 3 мм ∙ 5/2 = 7,5 мм. Таким образом, зная, что 45 мин = 0,75 ч, получим окончательно, что средняя скорость верхнего края столбика составила 7,5 мм/0,75 ч = 10 мм/ч.
Ответ: 10 мм/ч.
Критерии оценки:
1.Нахождение совмещённых рисок – 1 балл.
2.Связь между делениями двух шкал – 2 балла.
3.Приведение величин к миллиметрам и часам – 1 балл.
4.Окончательный ответ на вопрос задачи – 1 балл.
№2
Понадобятся две мензурки, вода и песок. В одну мензурку налейте 100 мл воды (мензурка должна быть заполнена не доверху), а в другую насыпьте 50 мл сухого песка. Затем пересыпьте песок в воду. Если, например, уровень воды поднялся до отметки 130 мл, то общий объём песчинок равен 30 мл. Таким образом, объём песчинок составляет 30/50 = 0,6 общего объёма песка, т.е. 60%. Остальные 40% занимает воздух.
Критерии оценки:
1.Перечислено оборудование, необходимое для измерений – 1 балл.
2.Определён объём песчинок – 2 балла.
3.Определён объём воздуха – 2 балла.
№3
Чтобы узнать необходимое время для подъёма, посчитаем время, затрачиваемое на один цикл, общее количество циклов и возможный остаток пути, который мог не войти в целый цикл. Найдём расстояние, которое Петя проходит за один цикл:
𝑆 = 0,5 м/c · 180 c − 0,2 м/c · 45 c + 0,3 м/c · 40 c = 93 м.
Время одного цикла 𝑇 равно 𝑇 = 180 + 55 + 45 + 40 = 320 с. Всего получается 10 полных циклов, и после остается еще 20 м, которые Петя пройдет со скоростью 0,5 м/с за время 𝑇′. Значит, общее затраченное время 𝑡 равно: 𝑡 = 𝑇 + 𝑇′ = 320 · 10 +20 ∙ 0,5 = 3240 c = 54 мин.
Ответ: 54 мин.
Критерии оценки:
1.Произведён расчёт расстояния, пройденного Петей за один цикл – 2 балла.
2.Вычислено время подъёма за один цикл – 1 балл.
3.Указано количество полных циклов подъёма – 1 балл.
4.Вычислено общее время подъёма Пети – 1 балл.
8 класс
№1
Найдём расход бензина грузового автомобиля: 𝑣 = 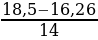 = 0,16 л/км. Тогда во время пути из 𝐴 в 𝐵 будет израсходовано бензина 150 · 0,16 = 24 л, а во время пути из 𝐴 в 𝐶 будет израсходовано 90 · 0,16 = 14,4 л. Соответственно на путь из 𝐶 в 𝐵 будет израсходовано бензина 24 + 2,4 − 14,4 = 12 л. Тогда расстояние между пунктами 𝐵 и 𝐶 равно 12/0,16 = 75 км.
= 0,16 л/км. Тогда во время пути из 𝐴 в 𝐵 будет израсходовано бензина 150 · 0,16 = 24 л, а во время пути из 𝐴 в 𝐶 будет израсходовано 90 · 0,16 = 14,4 л. Соответственно на путь из 𝐶 в 𝐵 будет израсходовано бензина 24 + 2,4 − 14,4 = 12 л. Тогда расстояние между пунктами 𝐵 и 𝐶 равно 12/0,16 = 75 км.
Ответ: 75 км.
Критерии оценивания:
1.Найден расход бензина грузового автомобиля – 1 балл.
2.Найден расход бензина на пути из А в В и из А в С – 2 балла.
3.Найден расход бензина на пути из С в В – 1 балл.
4.Найдено расстояние между пунктами В и С – 1 балл.
№2
Цепь передает на зубчики задней шестерёнки скорость зубчиков передней шестерёнки, таким образом, скорость зубчиков задней шестерёнки равна 10 см/с. Далее, используя равенство угловых скоростей для дисков с общей осью, получаем, что скорость точек на шине колеса равна скорости зубчиков шестерёнки заднего колеса, умноженной на отношение радиусов заднего колеса и задней шестерёнки: 𝑣 = 10 · 10 см/с = 100 см/с.
Ответ: 100 см/с.
Критерии оценивания:
1.Определена скорость зубчиков задней шестерёнки – 2 балла.
2.Используется условие равенства угловых скоростей для дисков с общей осью – 1 балл.
3.Определена скорость точки на шина заднего колеса – 2 балла.
№3
Из условия равновесия лёгкого поршня следует, что давление непосредственно над поршнем равно р. Тогда давление у верхнего торца поплавка равно: р1 = р – ρ0gh. Запишем условие равновесия поплавка: р1S + mg = pS. Учитывая, что m = ρ4hS, получаем следующее выражение: (р – ρ0gh)S + ρ4hSg = pS. Отсюда находим: ρ = ρ0/4 = 200 кг/м3.
Ответ: 200 кг/м3.
Критерии оценивания:
1.Найдено давление непосредственно над поршнем – 1 балл
2.Записоно выражение для давления сверху поплавка – 1 балл.
3.Записано условие равновесия поплавка с учётом выражения для массы – 2 балла.
4.Определено значение плотности поплавка – 1 балл.
№4
Больше всего теплоты было передано телу 4. Его координата по оси Q самая большая. Если при нагревании твёрдого тела к нему подводится количество теплоты Q = cm∆t, то его температура повышается на ∆t = Q/cm. На координатной плоскости (c,Q) для всех тел, имеющих одинаковую массу, температура которых повысилась на одинаковую величину Δt, соответствующие точки лежат на одной прямой, проходящей через начало координат, так как для них отношение Q/mc одно и то же. Из этого следует, что изменения температуры тел 2 и 3 одинаковы. Чем больше было повышение температуры, тем больше стало отношение Q/mc, а прямая, проведённая из начала координат, пойдёт под меньшим углом. Из этого следует, что больше всего нагрелось тело 5, а меньше всего тело 1.
 с
с


 1
1
2


3 4
 5
5

0 Q
Критерии оценивания:
1.Определено тело, которому передано больше всего теплоты с обоснованием – 1 балл.
2.Отмечено, что наклон прямой на графике связан с изменением температуры – 1 балл.
3.Найдено тело с максимальным изменением температуры – 1 балл.
4.Найдено тело с минимальным изменением температуры – 1 балл.
5.Найдены тела с одинаковым изменением температуры – 1 балл.
9 класс
№1
Сила упругости пружины динамометра во всех случаях одинакова. Напишем равенство сил действующих на метеорит при первом и втором взвешиваниях:
𝑘𝑥1 = 𝑘𝑥2 + 𝜌А𝑉𝑔 ⇒, 𝑘(𝑥1 – 𝑥2) = 𝜌А𝑉𝑔.
Напишем равенство сил, действующих на метеорит при первом и третьем взвешиваниях:
𝑘𝑥1 = 𝑘𝑥3 + 𝜌В𝑉𝑔 ⇒, 𝑘(𝑥1 – 𝑥3) = 𝜌В𝑉𝑔.
Выразив коэффициент 𝑘 из одного уравнения и подставив его в другое, получим отношение плотностей жидкостей:
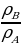 =
= 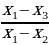 =
= 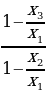 =
= 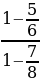 ≈ 1,33.
≈ 1,33.
Ответ: ≈ 1,33.
Критерии оценивания:
1.Указано условие постоянства силы упругости при всех взвешиваниях – 1 балл.
2.Записано равенство сил при первом и втором взвешиваниях – 1 балл.
3.Записано равенство сил при первом и третьем взвешиваниях – 1 балл.
4.Получена формула для расчёта отношения плотностей жидкостей – 2 балла.
Примечание: участники олимпиады могут получить соотношение плотностей наоборот 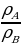 . В этом случае задача оценивается также в полный балл.
. В этом случае задача оценивается также в полный балл.
№2
Обозначим s – весь путь автомобиля, t – всё время движения автомобиля. По условию задачи имеем: v2 = vср = 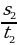 , где s2 = s –
, где s2 = s – 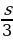 –
– 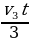 – путь, пройденный автомобилем на втором участке, t3 – время движения автомобиля на третьем участке; t2 = t –
– путь, пройденный автомобилем на втором участке, t3 – время движения автомобиля на третьем участке; t2 = t – 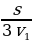 –
– 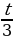 – время движения на втором участке. Получаем выражение: vср =
– время движения на втором участке. Получаем выражение: vср = 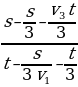 . Поделим числитель и знаменатель на t и приведём подобные. В результате получим: vср =
. Поделим числитель и знаменатель на t и приведём подобные. В результате получим: vср = 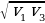 = 40 км/ч.
= 40 км/ч.
Ответ: vср = 40 км/ч.
Критерии оценивания:
1.Получено выражение для пути на втором участке – 1 балл.
2.Получено выражение для времени на втором участке – 1 балл.
3.Получено выражение для средней скорости – 2 балла.
4.Проведён правильно числовой расчёт – 1 балл.
№3
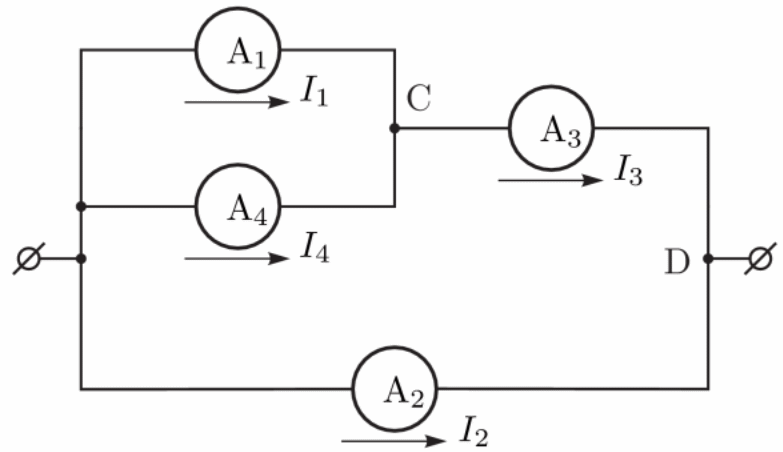 Пронумеруем амперметры слева направо (смотри рисунок 1). Все амперметры имеют одинаковое сопротивление. Обозначим его как r. Изобразим эквивалентную схему цепи (смотри рисунок 2).
Пронумеруем амперметры слева направо (смотри рисунок 1). Все амперметры имеют одинаковое сопротивление. Обозначим его как r. Изобразим эквивалентную схему цепи (смотри рисунок 2).
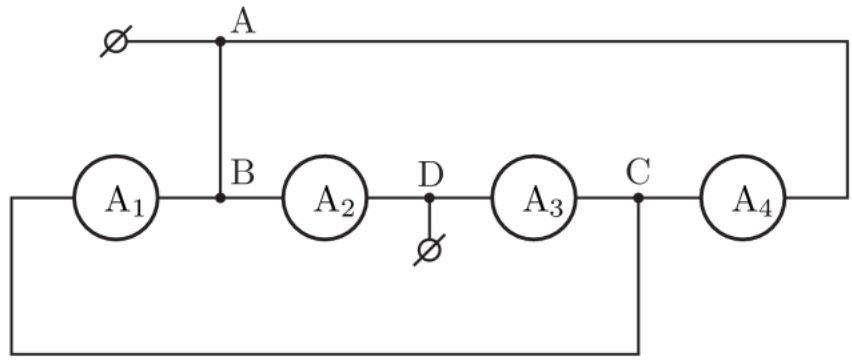
Рис.1 Рис.2
Имеем: I1 = I4 = I, I3 = I1 + I4 = 2I. Напряжение на источнике равно: U = I1r + I3r = 3Ir = I2r. Отсюда находим: I2 = 3I. По условию задачи I0 = I1 + I2 + I3 + I4 = 7I. Отсюда I = I0/7 – 7 мА. Искомая сила тока через перемычку АВ равна: IAB = I1 + I2 = 28 мА.
Ответ: 28 мА.
Критерии оценивания:
1.Указано, что все амперметры имеют одинаковое сопротивление – 1 балл.
2.Найдена сила тока I1 – 1 балл.
3.Найдена сила тока I2 – 1 балл.
4.Записана формула для силы тока через перемычку АВ – 1 балл.
5.Найдена сила тока через перемычку АВ – 1 балл.
№4
Больше всего теплоты было передано телу 4. Его координата по оси Q самая большая. Если при нагревании твёрдого тела к нему подводится количество теплоты Q = cm∆t, то его температура повышается на ∆t = Q/cm. На координатной плоскости (c,Q) для всех тел, имеющих одинаковую массу, температура которых повысилась на одинаковую величину Δt, соответствующие точки лежат на одной прямой, проходящей через начало координат, так как для них отношение Q/mc одно и то же. Из этого следует, что изменения температуры тел 2 и 3 одинаковы. Чем больше было повышение температуры, тем больше стало отношение Q/mc, а прямая, проведённая из начала координат, пойдёт под меньшим углом. Из этого следует, что больше всего нагрелось тело 5, а меньше всего тело 1.
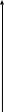
 с
с


 1
1
2


3 4
 5
5

0 Q
Критерии оценивания:
1.Определено тело, которому передано больше всего теплоты с обоснованием – 1 балл.
2.Отмечено, что наклон прямой на графике связан с изменением температуры – 1 балл.
3.Найдено тело с максимальным изменением температуры – 1 балл.
4.Найдено тело с минимальным изменением температуры – 1 балл.
5.Найдены тела с одинаковым изменением температуры – 1 балл.
№5
Сделаем пояснительный рисунок (смотри ниже). Из рисунка находим, что ∆SOB подобен ∆АВС и ∆SOE подобен ∆DEF, Тогда можно записать: 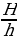 =
= 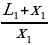 =
= 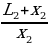 . По условию задачи имеем: L2 = L1 + ∆L и х2 = х1 + ∆х. Решая полученную систему уравнений, находим:
. По условию задачи имеем: L2 = L1 + ∆L и х2 = х1 + ∆х. Решая полученную систему уравнений, находим:
H = h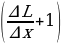 = 3,6 м.
= 3,6 м.

 S
S

 H
H
A D
h
h
x1 x2
O C B F E
 L1 ∆L
L1 ∆L
L2
Ответ: 3,6 м.
Критерии оценивания:
1.Сделан пояснительный чертёж и указаны подобные треугольники – 1 балл.
2.Записаны соотношения между сторонами подобных треугольников – 2 балла.
3.Получено выражение для высоты фонарного столба и проведён расчёт – 2 балла.
10 класс
№1
Горизонтальная составляющая скорости камня равна: vx = 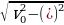 (смотри рисунок). Перемещение по горизонтали равно: L = vxt = t
(смотри рисунок). Перемещение по горизонтали равно: L = vxt = t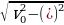 . Отсюда получаем биквадратное уравнение: t4 –
. Отсюда получаем биквадратное уравнение: t4 – 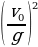 t2 +
t2 + 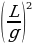 = 0. Корни этого уравнения: t1 = 1,5 c, t2 = 2 с.
= 0. Корни этого уравнения: t1 = 1,5 c, t2 = 2 с.

 v0
v0
gt
 vx
vx
Ответ: t1 = 1,5 c, t2 = 2 с.
Критерии оценивания:
1.Получено выражение для горизонтальной составляющей скорости камня – 2 балла.
2.Записано выражение для перемещения камня по горизонтали – 1 балл.
3.Получены значения для времени подъёма камня до максимальной высоты – 2 балла.
№2
Равновесие возможно, если существуют отличные от нуля силы реакции грузов и планки и силы натяжения нитей. Для нахождения сил натяжения рассмотрим только внешние силы, действующие на систему грузы+блоки+планка. Правила моментов относительно точек О1 и О2, лежащих на линиях действия сил натяжения верхних нитей (смотри рисунок ниже), имеют вид:
Mgx + 2T26x = 2mg3x + mg7x (относительно точки О1),
mgx + 2T16x = 2mg3x + Mg7x (относительно точки О2).
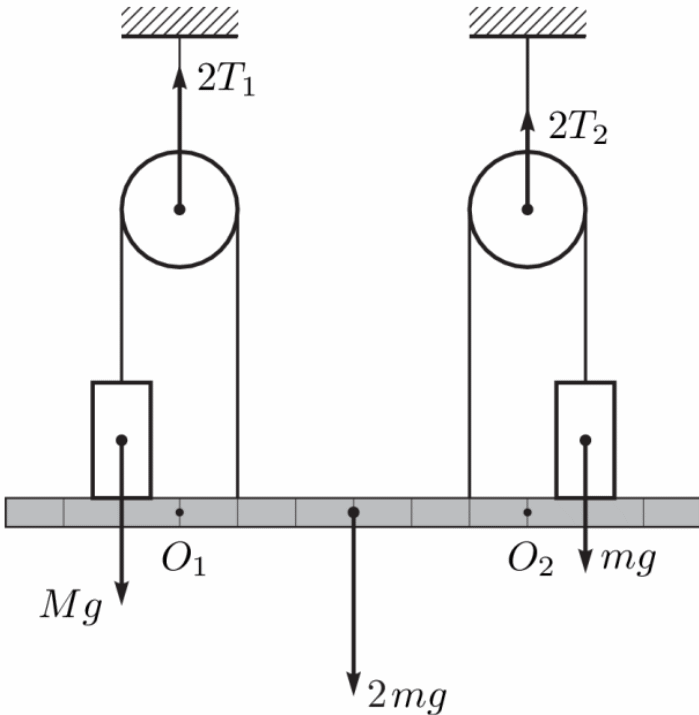
Из этих уравнений находим: T1 = 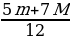 g, T2 =
g, T2 = 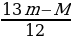 g. Видно, что левая нить не провисает при любых массах М, а правая натянута при M m. Запишем условия равновесия для каждого из грузов: Mg = T1 + N1, mg = T2 + N2. Откуда с учётом выражений для сил натяжения силы реакции равны: N1 = 5(M – m)g/12, N2 = (M – m)g/12. Положительные значения сил натяжения будут только при условии M m. Итак, равновесие возможно при выполнении условия: m M m.
g. Видно, что левая нить не провисает при любых массах М, а правая натянута при M m. Запишем условия равновесия для каждого из грузов: Mg = T1 + N1, mg = T2 + N2. Откуда с учётом выражений для сил натяжения силы реакции равны: N1 = 5(M – m)g/12, N2 = (M – m)g/12. Положительные значения сил натяжения будут только при условии M m. Итак, равновесие возможно при выполнении условия: m M m.
Ответ: m M m.
Критерии оценивания:
1.Записаны уравнения моментов для системы – 1 балл.
2.Получено условие для натянутых нитей – 1 балл.
3.Записаны уравнения равновесия грузов – 1 балл.
4.Получены условия сохранения контакта грузов и планки – 1 балл.
5.Явно записан диапазон значений для М – 1 балл.
№3
Пусть объём сосуда равен V0, а объём детали V1. Запишем уравнение теплового баланса для первого и второго случаев:
с1ρ1V1(tд – tх) = с0ρ0(V0 – V1)(tх – t0),
с1ρ12V1(tд – tу) = с0ρ0(V0 – 2V1)(tу – t0).
Преобразуем полученные выражения:
с1ρ1V1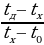 + с0ρ0V1 = с0ρ0V0,
+ с0ρ0V1 = с0ρ0V0,
с1ρ1(2V1)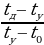 + с0ρ0(2V1) = с0ρ0V0.
+ с0ρ0(2V1) = с0ρ0V0.
Так как равны правые части, то равны и левые части, а объём V1 можно сократить. Тогда получаем:
с1ρ1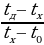 + с0ρ0 = 2с1ρ1
+ с0ρ0 = 2с1ρ1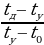 + 2с0ρ0.
+ 2с0ρ0.
Отсюда находим: с1 = с0 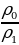
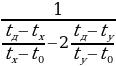 = 919,642 Дж/(кг∙0С).
= 919,642 Дж/(кг∙0С).
Ответ: 919,642 Дж/(кг∙0С).
Критерии оценивания:
1.Записано уравнение теплового баланса для первого случая – 1 балл.
2.Записано уравнение теплового баланса для второго случая – 1 балл.
3.Получена формула для расчёта искомой теплоёмкости – 2 балла.
4.Проведены вычисления – 1 балл.
№4
 Пронумеруем амперметры слева направо (смотри рисунок 1). Все амперметры имеют одинаковое сопротивление. Обозначим его как r. Изобразим эквивалентную схему цепи (смотри рисунок 2).
Пронумеруем амперметры слева направо (смотри рисунок 1). Все амперметры имеют одинаковое сопротивление. Обозначим его как r. Изобразим эквивалентную схему цепи (смотри рисунок 2).

Рис.1 Рис.2
Имеем: I1 = I4 = I, I3 = I1 + I4 = 2I. Напряжение на источнике равно: U = I1r + I3r = 3Ir = I2r. Отсюда находим: I2 = 3I. По условию задачи I0 = I1 + I2 + I3 + I4 = 7I. Отсюда I = I0/7 – 7 мА. Искомая сила тока через перемычку АВ равна: IAB = I1 + I2 = 28 мА.
Ответ: 28 мА.
Критерии оценивания:
1.Указано, что все амперметры имеют одинаковое сопротивление – 1 балл.
2.Найдена сила тока I1 – 1 балл.
3.Найдена сила тока I2 – 1 балл.
4.Записана формула для силы тока через перемычку АВ – 1 балл.
5.Найдена сила тока через перемычку АВ – 1 балл.
№5
В десятичном времени путешествие длилось 67940 − 35678 = 32262 дес. секунд. По условию 50000 дес. секунд = 12 час. Следовательно, 32262 дес. секунд = 7,743 ч. Расстояние от Парижа до Версаля и обратно равно 2·5,2·4 км = 41,6 км. Откуда vср ≈ 5,4 км/ч.
Ответ: ≈ 5,4 км/ч.
Критерии оценивания:
1.Найдена длительность путешествия в десятичном времени – 1 балл.
2.Перевод времени в обычные часы – 2 балла.
3.Перевод пути из лье в километры – 1 балл
4.Вычислена средняя путевая скорость курьера – 1 балл.
11 класс
№1
Пусть Баг находился вначале электрички, а Глюк стоял на линии ОО', где повстречались поезд и электричка (смотри рисунок а ниже).
О' электричка

 скорый поезд
скорый поезд
Р
 ис.а
ис.а

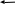
Р
 ис.б
ис.б
А О
Рассмотрим ситуацию через 13 секунд (смотри рисунок б выше), когда Баг поравнялся с концом скорого поезда. Получается, что расстояние ОА Баг проехал за время t2 = 13 с. Потом конец скорого поезда то же самое расстояние ОА проехал за время t = t1 – t2 = 10 c. Следовательно скорый поезд ехал быстрее электрички в К = t2/t = 1,3 раза. С другой стороны, каждый из поездов прошёл расстояние равное своей длине за одно и то же время t1 = 23 с. Это могло быть только в том случае, если скорый поезд длиннее электрички в К = 1,3 раза.
Ответ: в 1,3 раза.
Критерии оценивания:
1.Есть пояснительный рисунок – 1 балл.
2.Найдено отношение скоростей поезда и электрички – 2 балла.
3.Найдено отношение длины поезда к длине электрички – 2 балла.
№2
Расставим силы, действующие на грузы, блоки и нити (смотри рисунок ниже). Выберем ось Оу вертикально и направим её вниз. Начало отсчёта совместим с осями неподвижных блоков. Обозначим координаты грузов в некоторый момент времени как у1, у2, у3. Пусть проекции ускорений грузов на ось Оу равны ау1, ау2, ау3, а сила натяжения нити, связывающей грузы m1 и m2 равна Т. По условию задачи все блоки невесомы.

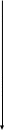



0
 Т Т Т Т Т
Т Т Т Т Т


 m1
m1
 у1
у1
m1g

 Т
Т
 у2 m2
у2 m2
 у3 m3
у3 m3
m2g
у m3g
Запишем уравнения движения грузов в проекциях на ось Оу:
m1g – T = m1ay1,
m2g – 4T = m2ay2,
m3g – T = m3ay3.
Отсюда находим: ay1 = g – 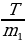 , ay2 = g –
, ay2 = g – 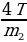 , ay3 = g –
, ay3 = g – 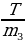 . По условию задачи нить нерастяжима и невесома, т.е. её длина постоянна. Значит, можно записать у1 + 4у2 + у3 = const. Тогда сумма проекций ускорений грузов должна быть равна нулю, т.е. ау1 + 4ау2 + ау3 = 0. Значит, получаем выражение: g –
. По условию задачи нить нерастяжима и невесома, т.е. её длина постоянна. Значит, можно записать у1 + 4у2 + у3 = const. Тогда сумма проекций ускорений грузов должна быть равна нулю, т.е. ау1 + 4ау2 + ау3 = 0. Значит, получаем выражение: g – 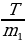 + 4g –
+ 4g – 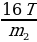 + g –
+ g – 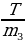 = 0. Отсюда находим силу натяжения нити:
= 0. Отсюда находим силу натяжения нити:
Т = 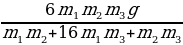 = 7,2 Н.
= 7,2 Н.
Ускорение груза m2 равно: ау2 = g – 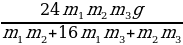 = 0,4 м/с2.
= 0,4 м/с2.
Ответ: 7,2 Н, 0,4 м/с2.
Критерии оценивания:
1.Расставлены силы, действующие на грузы, блоки и нити – 1 балл.
2.Записаны законы движения грузов на ось Оу с учётом невесомости блоков и нитей – 1 балл.
3.Записаны условия нерастяжимости нити – 1 балл.
4.Получено выражение для силы натяжения нити и проведён её числовой расчёт – 1 балл.
5.Получено выражение для ускорения второго груза и проведён числовой расчёт – 1 балл.
№3
По условию задачи трение в системе отсутствует, а сопротивлением воздуха пренебрегаем. Поэтому система кубики+поверхность+земля является замкнутой в направлении движения кубиков. Применим закон сохранения импульса для неупругого столкновения кубиков (ось Ох направим в направлении движения кубиков):
mv = (m + M)v1.
Отсюда находим скорость налетающего кубика: v = 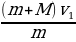 = 4v1. Путь L кубики проходят дважды. Время прохождения этого пути равно: t1 =
= 4v1. Путь L кубики проходят дважды. Время прохождения этого пути равно: t1 = 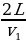 , v1 – скорость кубиков после неупругого удара. Когда кубики начинают действовать на пружину, в ней возникает сила упругости, которая возрастает от нуля до некоторого максимального значения. При максимальном сжатии пружины скорость кубиков станет равна нулю, и они под действием уменьшающейся силы упругости станут двигаться в обратную сторону набирая скорость. Когда деформация пружины станет равной нулю кубики иметь скорость, равную по модулю до начала сжатия пружины. Все эти процессы занимают время равное половине периода колебаний пружинного маятника с массой 4m, т.е. t2 = 2π
, v1 – скорость кубиков после неупругого удара. Когда кубики начинают действовать на пружину, в ней возникает сила упругости, которая возрастает от нуля до некоторого максимального значения. При максимальном сжатии пружины скорость кубиков станет равна нулю, и они под действием уменьшающейся силы упругости станут двигаться в обратную сторону набирая скорость. Когда деформация пружины станет равной нулю кубики иметь скорость, равную по модулю до начала сжатия пружины. Все эти процессы занимают время равное половине периода колебаний пружинного маятника с массой 4m, т.е. t2 = 2π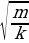 . Таким образом, общее время движения грузов равно: t = t1 + t2 =
. Таким образом, общее время движения грузов равно: t = t1 + t2 = 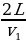 + 2π
+ 2π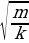 . Отсюда находим скорость v1: v1 =
. Отсюда находим скорость v1: v1 = 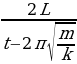 . Тогда скорость кубика массы m до его столкновения с кубиком массы М равна: v =
. Тогда скорость кубика массы m до его столкновения с кубиком массы М равна: v = 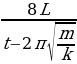 ≈ 1,44 м/с.
≈ 1,44 м/с.
Ответ: ≈ 1,44 м/с.
Критерии оценивания:
1.Указаны условия применимости закона сохранения импульса – 1 балл.
2.Получена формула для полного времени движения кубиков – 2 балла.
3.Получена формула для скорости движения кубиков после их столкновения – 1 балл.
4.Получена формула для расчёта скорости кубика массы m и проведён её расчёт – 1 балл.
№4
Пусть объём сосуда равен V0, а объём детали V1. Запишем уравнение теплового баланса для первого и второго случаев:
с1ρ1V1(tд – tх) = с0ρ0(V0 – V1)(tх – t0),
с1ρ12V1(tд – tу) = с0ρ0(V0 – 2V1)(tу – t0).
Преобразуем полученные выражения:
с1ρ1V1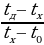 + с0ρ0V1 = с0ρ0V0,
+ с0ρ0V1 = с0ρ0V0,
с1ρ1(2V1)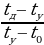 + с0ρ0(2V1) = с0ρ0V0.
+ с0ρ0(2V1) = с0ρ0V0.
Так как равны правые части, то равны и левые части, а объём V1 можно сократить. Тогда получаем:
с1ρ1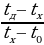 + с0ρ0 = 2с1ρ1
+ с0ρ0 = 2с1ρ1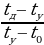 + 2с0ρ0.
+ 2с0ρ0.
Отсюда находим: с1 = с0 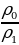
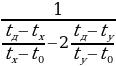 = 919,642 Дж/(кг∙0С).
= 919,642 Дж/(кг∙0С).
Ответ: 919,642 Дж/(кг∙0С).
Критерии оценивания:
1.Записано уравнение теплового баланса для первого случая – 1 балл.
2.Записано уравнение теплового баланса для второго случая – 1 балл.
3.Получена формула для расчёта искомой теплоёмкости – 2 балла.
4.Проведены вычисления – 1 балл.
№5
При вращении проводника в постоянном магнитном поле, в нём возникает индукционный ток, который можно найти по закону Ома для замкнутой цепи: Ii = 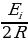 , где Ei – ЭДС индукции, возникающей в замкнутом проводящем контуре при вращении одной из стрелок в магнитном поле, R – сопротивление одной из стрелок. Стрелки соединены последовательно. Находим ЭДС индукции согласно закону электромагнитной индукции: Ei =
, где Ei – ЭДС индукции, возникающей в замкнутом проводящем контуре при вращении одной из стрелок в магнитном поле, R – сопротивление одной из стрелок. Стрелки соединены последовательно. Находим ЭДС индукции согласно закону электромагнитной индукции: Ei = 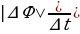 , где ∆Ф = В∆S – изменение магнитного потока через замкнутую поверхность, В – индукция магнитного поля, ∆S = L2∆α/2 – площадь сектора. Итак, имеем: Ei =
, где ∆Ф = В∆S – изменение магнитного потока через замкнутую поверхность, В – индукция магнитного поля, ∆S = L2∆α/2 – площадь сектора. Итак, имеем: Ei = 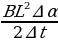 =
= 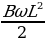 . Тогда сила тока, проходящего через стрелки, равна: Ii =
. Тогда сила тока, проходящего через стрелки, равна: Ii = 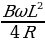 = 0,1 А.
= 0,1 А.
Ответ: 0,1 А.
Критерии оценивания:
1.Записан закон электромагнитной индукции – 1 балл.
2.Записана формула для изменения магнитного потока – 1 балл.
3.Записан закон Ома для замкнутой цепи – 1 балл.
4.Получена конечная формула для силы индукционного тока и проведён его расчёт – 2 балла.





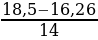 = 0,16 л/км. Тогда во время пути из 𝐴 в 𝐵 будет израсходовано бензина 150 · 0,16 = 24 л, а во время пути из 𝐴 в 𝐶 будет израсходовано 90 · 0,16 = 14,4 л. Соответственно на путь из 𝐶 в 𝐵 будет израсходовано бензина 24 + 2,4 − 14,4 = 12 л. Тогда расстояние между пунктами 𝐵 и 𝐶 равно 12/0,16 = 75 км.
= 0,16 л/км. Тогда во время пути из 𝐴 в 𝐵 будет израсходовано бензина 150 · 0,16 = 24 л, а во время пути из 𝐴 в 𝐶 будет израсходовано 90 · 0,16 = 14,4 л. Соответственно на путь из 𝐶 в 𝐵 будет израсходовано бензина 24 + 2,4 − 14,4 = 12 л. Тогда расстояние между пунктами 𝐵 и 𝐶 равно 12/0,16 = 75 км.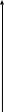
 с
с
 1
1 5
5
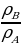 =
= 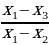 =
= 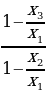 =
= 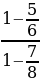 ≈ 1,33.
≈ 1,33.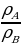 . В этом случае задача оценивается также в полный балл.
. В этом случае задача оценивается также в полный балл.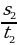 , где s2 = s –
, где s2 = s – 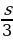 –
– 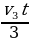 – путь, пройденный автомобилем на втором участке, t3 – время движения автомобиля на третьем участке; t2 = t –
– путь, пройденный автомобилем на втором участке, t3 – время движения автомобиля на третьем участке; t2 = t – 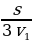 –
– 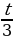 – время движения на втором участке. Получаем выражение: vср =
– время движения на втором участке. Получаем выражение: vср = 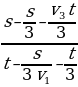 . Поделим числитель и знаменатель на t и приведём подобные. В результате получим: vср =
. Поделим числитель и знаменатель на t и приведём подобные. В результате получим: vср = 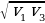 = 40 км/ч.
= 40 км/ч. Пронумеруем амперметры слева направо (смотри рисунок 1). Все амперметры имеют одинаковое сопротивление. Обозначим его как r. Изобразим эквивалентную схему цепи (смотри рисунок 2).
Пронумеруем амперметры слева направо (смотри рисунок 1). Все амперметры имеют одинаковое сопротивление. Обозначим его как r. Изобразим эквивалентную схему цепи (смотри рисунок 2).
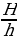 =
= 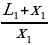 =
= 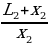 . По условию задачи имеем: L2 = L1 + ∆L и х2 = х1 + ∆х. Решая полученную систему уравнений, находим:
. По условию задачи имеем: L2 = L1 + ∆L и х2 = х1 + ∆х. Решая полученную систему уравнений, находим: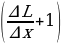 = 3,6 м.
= 3,6 м.

 S
S
 H
H
 L1 ∆L
L1 ∆L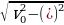 (смотри рисунок). Перемещение по горизонтали равно: L = vxt = t
(смотри рисунок). Перемещение по горизонтали равно: L = vxt = t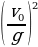 t2 +
t2 + 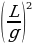 = 0. Корни этого уравнения: t1 = 1,5 c, t2 = 2 с.
= 0. Корни этого уравнения: t1 = 1,5 c, t2 = 2 с.
 v0
v0 vx
vx
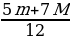 g, T2 =
g, T2 = 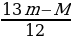 g. Видно, что левая нить не провисает при любых массах М, а правая натянута при M m. Запишем условия равновесия для каждого из грузов: Mg = T1 + N1, mg = T2 + N2. Откуда с учётом выражений для сил натяжения силы реакции равны: N1 = 5(M – m)g/12, N2 = (M – m)g/12. Положительные значения сил натяжения будут только при условии M m. Итак, равновесие возможно при выполнении условия: m M m.
g. Видно, что левая нить не провисает при любых массах М, а правая натянута при M m. Запишем условия равновесия для каждого из грузов: Mg = T1 + N1, mg = T2 + N2. Откуда с учётом выражений для сил натяжения силы реакции равны: N1 = 5(M – m)g/12, N2 = (M – m)g/12. Положительные значения сил натяжения будут только при условии M m. Итак, равновесие возможно при выполнении условия: m M m.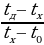 + с0ρ0V1 = с0ρ0V0,
+ с0ρ0V1 = с0ρ0V0,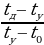 + с0ρ0(2V1) = с0ρ0V0.
+ с0ρ0(2V1) = с0ρ0V0.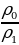
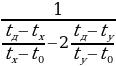 = 919,642 Дж/(кг∙0С).
= 919,642 Дж/(кг∙0С).
 скорый поезд
скорый поезд
 ис.а
ис.а


 m1
m1 у1
у1 
 Т
Т у2 m2
у2 m2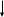 у3 m3
у3 m3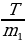 , ay2 = g –
, ay2 = g – 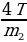 , ay3 = g –
, ay3 = g – 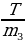 . По условию задачи нить нерастяжима и невесома, т.е. её длина постоянна. Значит, можно записать у1 + 4у2 + у3 = const. Тогда сумма проекций ускорений грузов должна быть равна нулю, т.е. ау1 + 4ау2 + ау3 = 0. Значит, получаем выражение: g –
. По условию задачи нить нерастяжима и невесома, т.е. её длина постоянна. Значит, можно записать у1 + 4у2 + у3 = const. Тогда сумма проекций ускорений грузов должна быть равна нулю, т.е. ау1 + 4ау2 + ау3 = 0. Значит, получаем выражение: g – 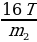 + g –
+ g – 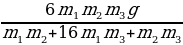 = 7,2 Н.
= 7,2 Н.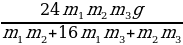 = 0,4 м/с2.
= 0,4 м/с2.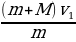 = 4v1. Путь L кубики проходят дважды. Время прохождения этого пути равно: t1 =
= 4v1. Путь L кубики проходят дважды. Время прохождения этого пути равно: t1 = 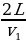 , v1 – скорость кубиков после неупругого удара. Когда кубики начинают действовать на пружину, в ней возникает сила упругости, которая возрастает от нуля до некоторого максимального значения. При максимальном сжатии пружины скорость кубиков станет равна нулю, и они под действием уменьшающейся силы упругости станут двигаться в обратную сторону набирая скорость. Когда деформация пружины станет равной нулю кубики иметь скорость, равную по модулю до начала сжатия пружины. Все эти процессы занимают время равное половине периода колебаний пружинного маятника с массой 4m, т.е. t2 = 2π
, v1 – скорость кубиков после неупругого удара. Когда кубики начинают действовать на пружину, в ней возникает сила упругости, которая возрастает от нуля до некоторого максимального значения. При максимальном сжатии пружины скорость кубиков станет равна нулю, и они под действием уменьшающейся силы упругости станут двигаться в обратную сторону набирая скорость. Когда деформация пружины станет равной нулю кубики иметь скорость, равную по модулю до начала сжатия пружины. Все эти процессы занимают время равное половине периода колебаний пружинного маятника с массой 4m, т.е. t2 = 2π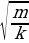 . Таким образом, общее время движения грузов равно: t = t1 + t2 =
. Таким образом, общее время движения грузов равно: t = t1 + t2 = 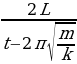 . Тогда скорость кубика массы m до его столкновения с кубиком массы М равна: v =
. Тогда скорость кубика массы m до его столкновения с кубиком массы М равна: v = 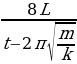 ≈ 1,44 м/с.
≈ 1,44 м/с.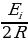 , где Ei – ЭДС индукции, возникающей в замкнутом проводящем контуре при вращении одной из стрелок в магнитном поле, R – сопротивление одной из стрелок. Стрелки соединены последовательно. Находим ЭДС индукции согласно закону электромагнитной индукции: Ei =
, где Ei – ЭДС индукции, возникающей в замкнутом проводящем контуре при вращении одной из стрелок в магнитном поле, R – сопротивление одной из стрелок. Стрелки соединены последовательно. Находим ЭДС индукции согласно закону электромагнитной индукции: Ei = 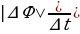 , где ∆Ф = В∆S – изменение магнитного потока через замкнутую поверхность, В – индукция магнитного поля, ∆S = L2∆α/2 – площадь сектора. Итак, имеем: Ei =
, где ∆Ф = В∆S – изменение магнитного потока через замкнутую поверхность, В – индукция магнитного поля, ∆S = L2∆α/2 – площадь сектора. Итак, имеем: Ei = 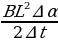 =
= 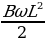 . Тогда сила тока, проходящего через стрелки, равна: Ii =
. Тогда сила тока, проходящего через стрелки, равна: Ii = 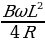 = 0,1 А.
= 0,1 А.









