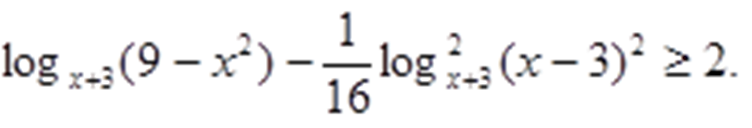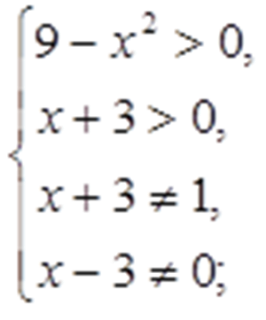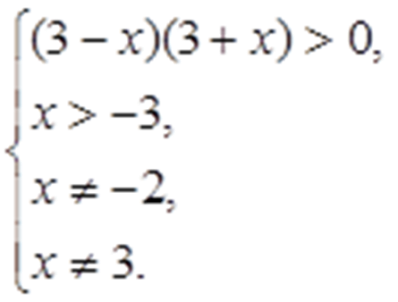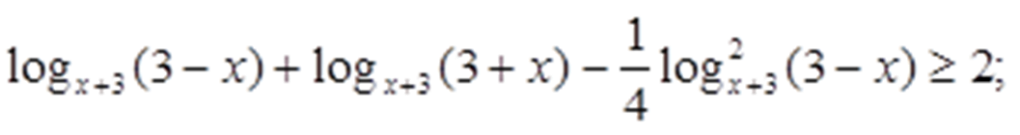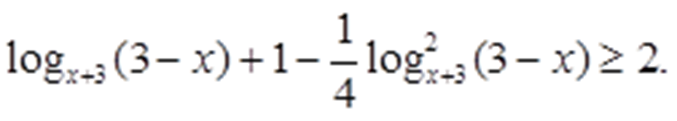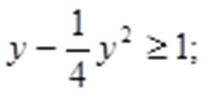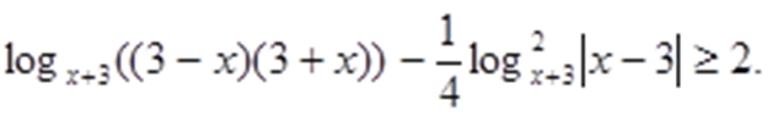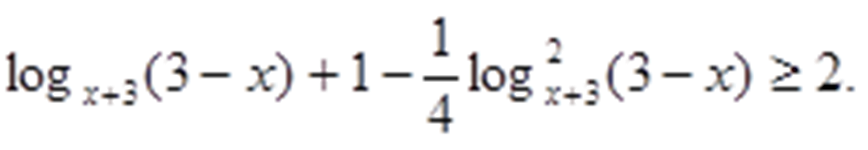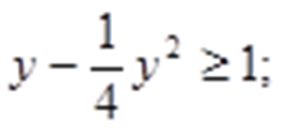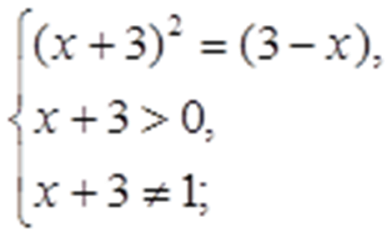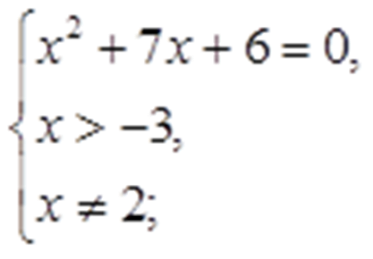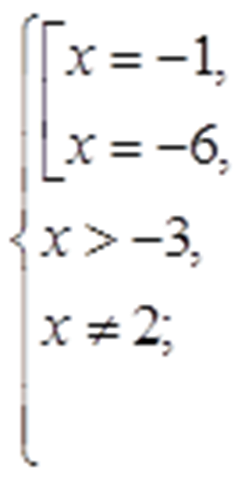Введение
Решение уравнений и неравенств - важный раздел в математике. Успешное изучение математики невозможно без умения решать разнообразные неравенства и уравнения, поэтому я решила взять в качестве темы научно-исследовательской работы один из способов решения неравенств и уравнений – метод мажорант. Этим методом можно решать нестандартные уравнения, уравнения повышенной сложности, уравнения или системы уравнений, в которых количество переменных превышает количество уравнений и задачи с параметром.
В данном исследовании, я узнала совершенно новый для себя способ решения уравнений-метод мажоранта, который встречается в ЕГЭ и мало изучается в школе. Так же научилась применять его непосредственно при решении уравнений и неравенств. Для этого я изучила и проанализировала материал по данной теме, на конкретных примерах училась применять метод мажоранта при решении уравнений и неравенств.
На всех этапах нашей работы возникали трудности. Например, вначале не всегда получалось определять, есть ли в данной задаче мажоранта или ее нет. По всем непонятным вопросам я консультировалась с учителем.
Цель работы:
- изучить метод мажорант, применить этот метод для решения нестандартных уравнений и неравенств.
Задачи проекта:
- изучить определения мажоранты функции и исследовать, какие функции имеют мажоранту;
- изучить метод мажоранта, применить этот метод для решения нестандартных уравнений и неравенств;
- привести примеры уравнений и неравенств, которые могут быть решены методом мажоранта.
Актуальность работы:
В последние годы в заданиях ЕГЭ по математике входят задания, как обязательного, так и повышенного уровня. Среди последних встречаются нестандартные математические задачи, в роли которых чаще всего выступают уравнения и неравенства. Одним из эффективных и оригинальных методов решения нестандартных уравнений и неравенств является метод мажорант. При этом в школьных учебниках алгебры и начал анализа материал о данном методе отсутствует.
Актуальность моей работы состоит в поиске эффективных средств и методов для изучения и освоения нестандартных методов решения уравнений и неравенств части С единого государственного экзамена и вступительных заданий. Метод мажорант – один из таких методов, который позволяет успешно решать олимпиадные задачи, конкурсные задачи, уравнения повышенной сложности по математике.
Определение мажоранты функции
Мажорантой данной функции f(х) на множестве Р (или множества А чисел) называется такое число М, что либо f(х) ≤ М для всех х ϵ Р, либо f(х) ≥ М для всех х ϵ Р (соответственно, х ≤ М для всех х из А, или х ≥ М для всех х из А).
Термин «мажоранта» происходит от французского слова «majorante», от «majorer» — объявлять большим.
Мажоранты многих элементарных функции известны. Их нетрудно указать, зная область значений функции.
Теория
Мажорирование – нахождение точек ограничения функции.
Метод мажорант — эффективный способ решения сложных и нестандартных уравнений и неравенств.
Мажоранта и миноранта – две функции, значение первой из которых не меньше, а второй - не больше соответствующих значений данной функции.
Этот нестандартный метод решения уравнений и неравенств заключается в том, что одна часть уравнения (или неравенства) ограничена сверху неким числом М, а другая часть уравнения (или неравенства) ограничена снизу этим же числом М, мажорантой.
При применении данного метода используется определение ограниченных функций.
Основная идея метода Мажоранта состоит в следующем. Пусть мы имеем уравнение f(x) = g(x) и существует такое M, что для любого x из области определения имеем f(x)≤M и g(x)≥M (или наоборот). Тогда исходное уравнение равносильно системе
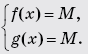
Опорные неравенства:
1. а) a+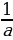 ≥2 при a 0, равенство a = 1;
≥2 при a 0, равенство a = 1;
б) a+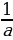 ≤2 при a
≤2 при a
2. 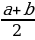 ≥
≥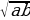 при a ≥ 0, b ≥ 0; равенство достигается при a = b.
при a ≥ 0, b ≥ 0; равенство достигается при a = b.
3. | a sinx + b cosx| ≤ 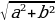
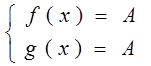 Теорема1. Пусть f(x) и g(x) – некоторые функции, определённые на множестве D. Пусть f(x) ограничена на этом множестве числом А сверху, а g(x) ограничена на этом множестве тем же числом А, но снизу. Тогда, уравнение f(x) = g(x) равносильно системе уравнений.
Теорема1. Пусть f(x) и g(x) – некоторые функции, определённые на множестве D. Пусть f(x) ограничена на этом множестве числом А сверху, а g(x) ограничена на этом множестве тем же числом А, но снизу. Тогда, уравнение f(x) = g(x) равносильно системе уравнений.
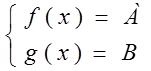 Теорема 2. Пусть f(x) и g(x) – некоторые функции, определённые на множестве D. Пусть f(x) и g(x) ограничены на этом множестве снизу (сверху) числами А и В соответственно. Тогда уравнение f(x) + g(x) = A+B равносильно системе уравнений
Теорема 2. Пусть f(x) и g(x) – некоторые функции, определённые на множестве D. Пусть f(x) и g(x) ограничены на этом множестве снизу (сверху) числами А и В соответственно. Тогда уравнение f(x) + g(x) = A+B равносильно системе уравнений
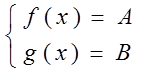 Теорема 3. Пусть f(x) и g(x) – некоторые неотрицательные функции, определённые на множестве D. Пусть f(x) ограничена сверху ( или снизу) числами А и В соответственно. Тогда уравнение f(x)·g(x)= А·B равносильно системе уравнений (при условии, что A0 и B0)
Теорема 3. Пусть f(x) и g(x) – некоторые неотрицательные функции, определённые на множестве D. Пусть f(x) ограничена сверху ( или снизу) числами А и В соответственно. Тогда уравнение f(x)·g(x)= А·B равносильно системе уравнений (при условии, что A0 и B0)
Примеры функций, имеющих мажоранту
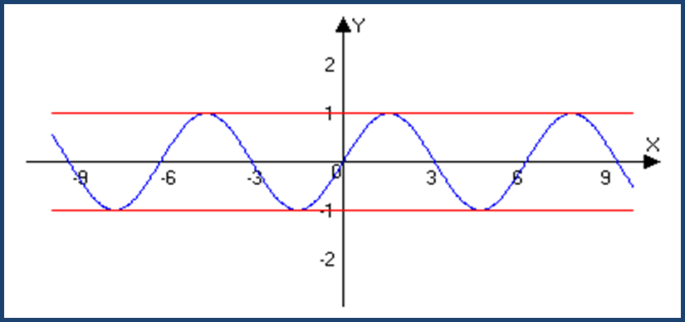
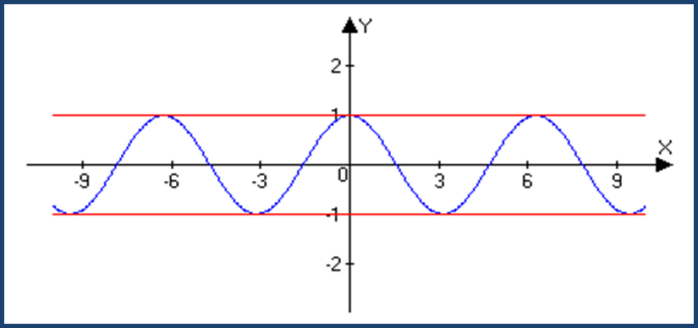
1.Тригонометрические функции.
f(x)=sin x f(x)=cos x
-1≤ sin x ≤ 1 -1≤cos x≤1
M=1, M=-1 M=1, M=-1
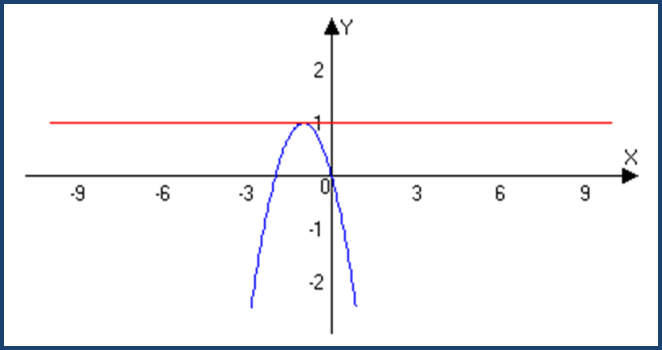
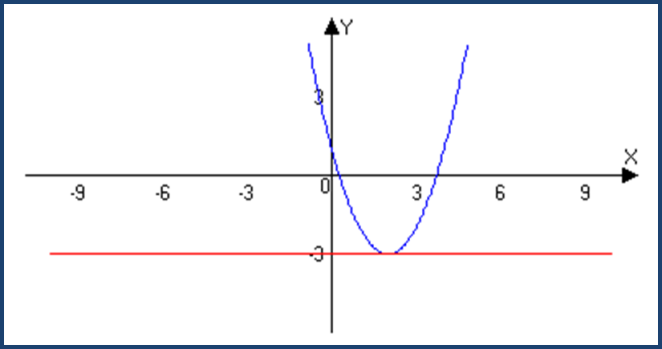
2.Квадратичная функция.
f(x)= ax²+bx+c,
(p ; n) -вершина параболы
M=n=(4ac-b²)/4a
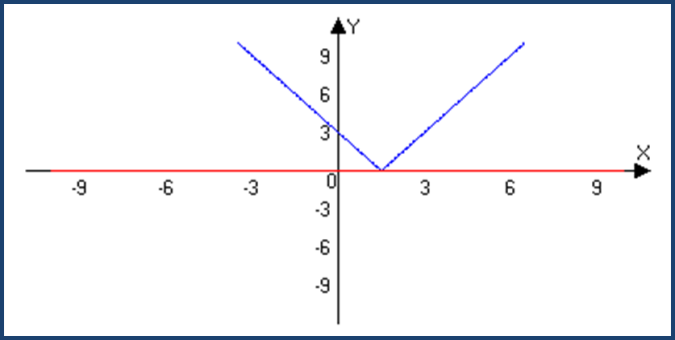
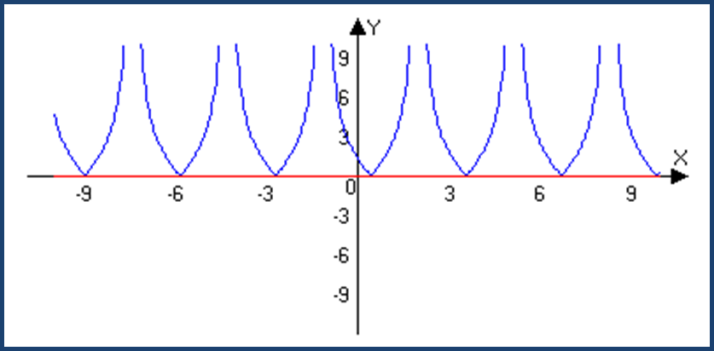
3. Функции, содержащие переменную под знаком модуля.
f(x)=|g(x)|
0 ≤|g(x)|
M=0
4.
Функции, содержащие переменную под знаком корня.
f(x)= √g(x)
0 ≤ √g(x)
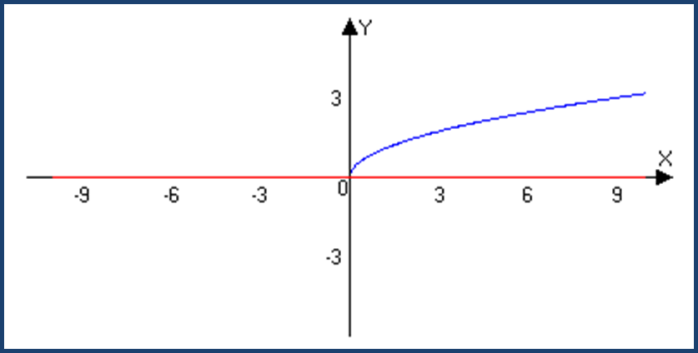
 M=0
M=0
Решение неравенств с помощью метода мажорант
Рассмотрим задания из демонстрационного варианта ЕГЭ 2015 учебного года, при решении которых можно использовать метод мажорант.
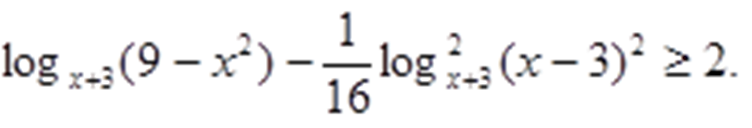
Решение 1.
Преобразуем неравенство:
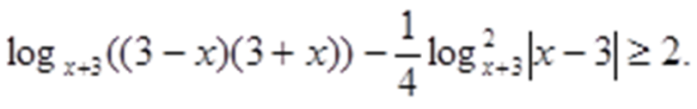
Найдем, при каких значениях х левая часть неравенства имеет смысл:
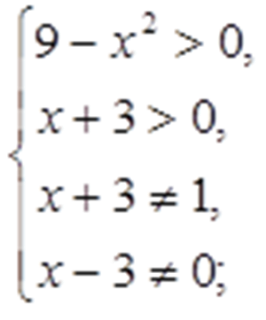
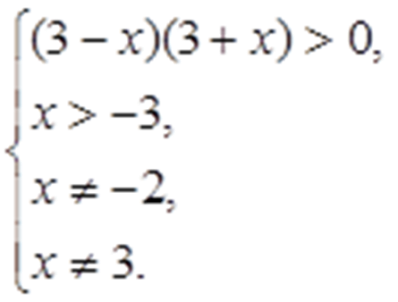

Получаем: -3
Значит, |x-3| = 3-x при всех допустимых значениях х. Поэтому
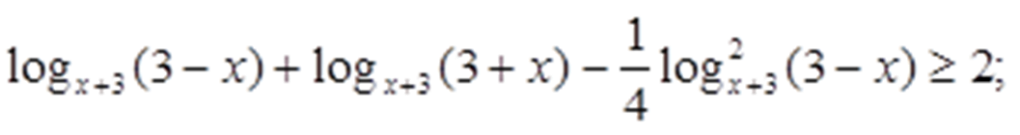
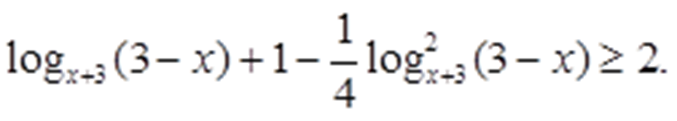
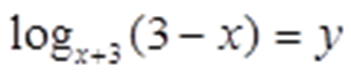
Сделаем замену:
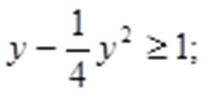
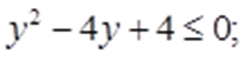
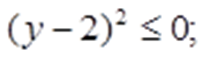
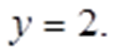
Получаем:
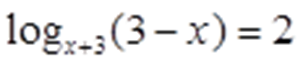
Таким образом:
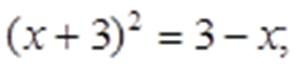
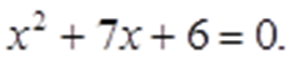 Откуда
Откуда
Корни уравнения: -6 и -1. Условию -3
Ответ:{-1}.
Решение 2.
Можно не находить область допустимых значений х, а прийти к соотношению |x-3|=3-x другим способом. Тогда решение будет немного короче.
Преобразуем неравенство:
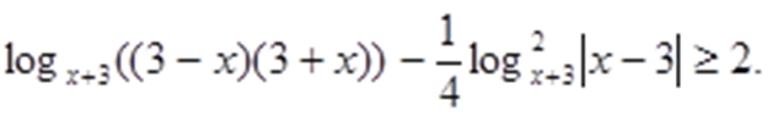
Заметим, что x+30 и (3-x)(3+x)0. Значит, 3-x0. Поэтому |x-3|=3-x.
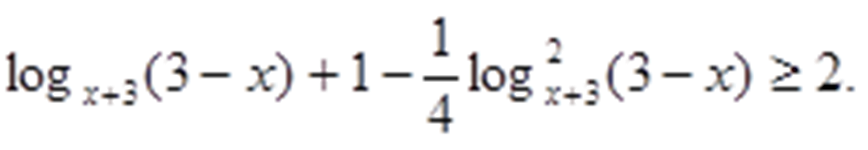
Получаем:
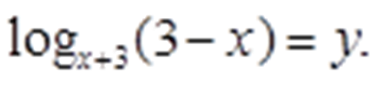
Сделаем замену:
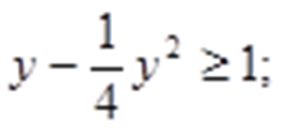
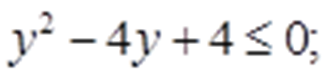
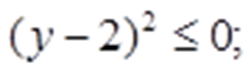
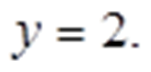
Получаем:
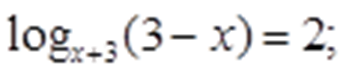
Таким образом,
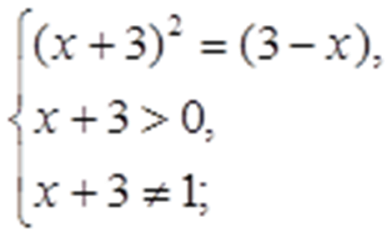
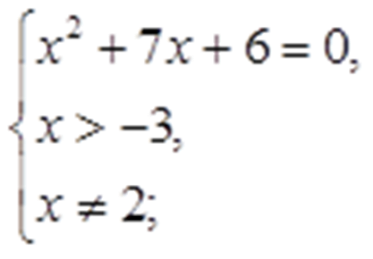
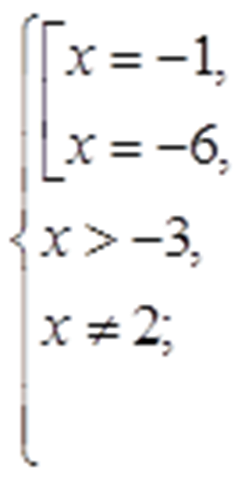
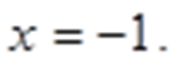
Ответ: {-1}.
Признаки присутствия мажоранты в задаче:
- Смешанное уравнение (или неравенство), т.е. в задании есть разнородные функции, например, логарифмическая и линейная, или квадратный трехчлен и тригонометрическая, или вообще несколько видов;
- Сложный, трехэтажный и пугающий вид, большие числа и коэффициенты.
Для нахождения мажоранты необходимы:
- Здравый смысл и нестандартный взгляд на вещи;
- Знание свойств функций;
- Умение исследовать функции на максимум, минимум, области значений и прочие характеристики;
- Умение преобразовывать функции, так, чтобы было проще вытащить мажоранту;
Заключение
Благодаря этой работе я узнала, что сложные уравнения и неравенства можно решать с помощью метода мажорант. Я научилась с помощью мажоранта решать уравнения и неравенства, содержащие рациональные, иррациональные и тригонометрические функции.
Список литературы
http://festival.1september.ru/articles/531858/
http://bse.sci-lib.com/article072548.html
https://ru.wiktionary.org/wiki/%D0%BC%D0%B0%D0%B6%D0%BE%D1%80%D0%B0%D0%BD%D1%82%D0%B0
lib.znate.ru/docs/index-4018.html
http://www.berdov.com/ege/parametr/metod-mazhorant/
http://nsportal.ru/shkola/algebra/library/2012/08/05/ispolzovanie-metoda-mazhoranta-pri-reshenii-uravneniy-i-neravenstv
Аляева О.Н. Использование ограниченности функций при решении конкурсных задач [электронный ресурс] // Zavuch.ru : [сайт]. URL : http://www.zavuch.info/index.php
Вариант ЕГЭ 2011. Математика [электронный ресурс] // Zavuch.info : [сайт]. URL : http://www.zavuch.info/metodichka/tochnie/algebra/algdidact
Кожухов И. Б., Прокофьев А.А. Математика. Полный справочник / И.Б. Кожухов, А.А. Прокофьев. – М.: Махаон, 2007. – 352 с.
Корянов А.Г. Математика. ЕГЭ 2010. Задания типа С1-С6. Методы решения [электронный ресурс] // Аlleng.ru : [сайт]. URL : http://www.alleng.ru/d/math/math468.htm





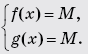
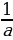 ≥2 при a 0, равенство a = 1;
≥2 при a 0, равенство a = 1; 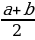 ≥
≥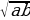 при a ≥ 0, b ≥ 0; равенство достигается при a = b.
при a ≥ 0, b ≥ 0; равенство достигается при a = b.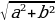
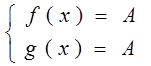 Теорема1. Пусть f(x) и g(x) – некоторые функции, определённые на множестве D. Пусть f(x) ограничена на этом множестве числом А сверху, а g(x) ограничена на этом множестве тем же числом А, но снизу. Тогда, уравнение f(x) = g(x) равносильно системе уравнений.
Теорема1. Пусть f(x) и g(x) – некоторые функции, определённые на множестве D. Пусть f(x) ограничена на этом множестве числом А сверху, а g(x) ограничена на этом множестве тем же числом А, но снизу. Тогда, уравнение f(x) = g(x) равносильно системе уравнений.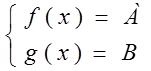 Теорема 2. Пусть f(x) и g(x) – некоторые функции, определённые на множестве D. Пусть f(x) и g(x) ограничены на этом множестве снизу (сверху) числами А и В соответственно. Тогда уравнение f(x) + g(x) = A+B равносильно системе уравнений
Теорема 2. Пусть f(x) и g(x) – некоторые функции, определённые на множестве D. Пусть f(x) и g(x) ограничены на этом множестве снизу (сверху) числами А и В соответственно. Тогда уравнение f(x) + g(x) = A+B равносильно системе уравнений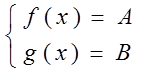 Теорема 3. Пусть f(x) и g(x) – некоторые неотрицательные функции, определённые на множестве D. Пусть f(x) ограничена сверху ( или снизу) числами А и В соответственно. Тогда уравнение f(x)·g(x)= А·B равносильно системе уравнений (при условии, что A0 и B0)
Теорема 3. Пусть f(x) и g(x) – некоторые неотрицательные функции, определённые на множестве D. Пусть f(x) ограничена сверху ( или снизу) числами А и В соответственно. Тогда уравнение f(x)·g(x)= А·B равносильно системе уравнений (при условии, что A0 и B0)






 M=0
M=0