бюджетное профессиональное образовательное учреждение
Вологодской области
«Череповецкий металлургический колледж имени академика И.П. Бардина»
Специальности
09.02.03 «Программирование
в компьютерных системах»,
09.02.01 «Компьютерные
системы и комплексы»
РЕШЕНИЕ ЗАДАЧ НА КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ
Методические указания и задания для практической работы по дисциплине «Теория вероятностей и математическая статистика» для студентов 2 курса.
Составитель: Корнилова Т.Н.,
преподаватель колледжа
2017
Решение задач на классическое определение вероятности. Методические указания и задания для практической работы для студентов 2 курса. /Составитель: Корнилова Т.Н./-Череповец: Череповецкий металлургический колледж имени академика И.П.Бардина, 2017. - 22 с.
Рецензент: Корчуганова И.Б., преподаватель колледжа
Данные методические рекомендации рассмотрены и одобрены цикловой комиссией физико-математических дисциплин
Председатель / / Масыгина И. А.
17 апреля 2017 г.
Протокол № 8
Содержание
| 1 | Цель работы | 4 |
| 2 | Теоретическое обоснование | 4 |
| 3 | Порядок выполнения работы | 9 |
| 4 | Контрольные вопросы | 9 |
| 5 | Рекомендации по оформлению отчёта по практической работе Литература Приложение А – Варианты заданий
| 9 10 11 |
Практическая работа
Решение задач на классическое определение вероятности.
Цель работы
события;
решения задач.
Теоретическое обоснование
Определение. Всякое действие, явление, наблюдение с несколькими различными исходами, реализуемое при данном комплексе условий, будем называть испытанием.
Пример.
1) Многократное подбрасывание монеты;
2) Процесс изготовления какой-то детали.
Определение. Результат этого действия или наблюдения будем называть событием.
Пример.
1). Появление герба при подбрасывании монеты – событие;
2). Выстрел по мишени – испытание;
3). Попадание в мишень – событие.
Обозначение.
События принято обозначать большими латинскими буквами: А, В, С …
Выделяют следующие виды событий.
Таблица 1 – виды событий
| Название | Определение | Пример |
| 1. Достоверное U. | Событие обязательно произойдет в результате данного испытания. | Выпадение от 1 до 6 очков на игральной кости. |
| 2. Невозможное V. | Событие, которое не может произойти в данном испытании. | Появление 11 очков при бросании игральной кости. |
| 3. Случайное. | Событие, которое в данном испытании может произойти, а может не произойти. | Попадание при выстреле по мишени. |
| 4. Несовместные события. | Появление одного события исключает появление другого. | В ящике находятся стандартные и бракованные детали. Выбирается одна деталь. Событие А: появление стандартной детали, Событие В: бракованной детали. События А и В – несовместные. |
| 5. Совместные события. | Появление одного события из двух не исключает появление другого.
| Брошена игральная кость. Событие А: появление 2 очков, Событие В: появление четного числа очков. События A и B совместны, так как могут произойти вместе. |
| 6. Равновозможные события. | Есть основания считать, что ни одно из этих событий не является более возможным, чем другие. | Выпадение того или иного числа очков на брошенной игральной кости – события равновозможные. |
| 7. Попарно несовместные события.
| В результате испытания может произойти только одно из этих событий.
| Производится два выстрела по мишени: Событие А: 2 попадания, Событие В: 1 попадание, Событие С: 2 промаха. События A, B, C – попарно несовместные, т.к. никакие два из них не могут произойти одновременно. |
| 8. Противоположные события А и  . . | В испытании одно из них происходит только в том случае, когда не происходит другое.
| Попадание и промах при выстреле – противоположные события. Они являются единственными исходами испытания. |
| 9. Полная система событий. | Несколько событий таких, что в результате опыта непременно должно произойти хоты бы одно из них.
| испытание: из ящика со стандартными и бракованными деталями наудачу извлекается 3 детали. События: А1: все 3 детали стандартные, А2:2 детали стандартные и 1 бракованная, А3:1 деталь стандартная и 2 бракованные, А4: 3 бракованные образуют полную группу и являются всеми возможными исходами испытания. |
Если несколько событий:
1) образуют полную группу;
2) несовместные;
3) равновозможные, то они называются случаями («шансами»).
Существует несколько определений вероятности. Приведем то, которое принято называть классическим.
Определение. Случай называется благоприятным событию, если появление этого случая влечет за собой появление события.
Пусть имеется полная группа попарно несовместных равновозможных событий.
Определение. Вероятностью наступления события А называется отношение числа исходов, благоприятствующих событию А, к числу всех исходов испытания.
Таким образом, вероятность события А определяется формулой:
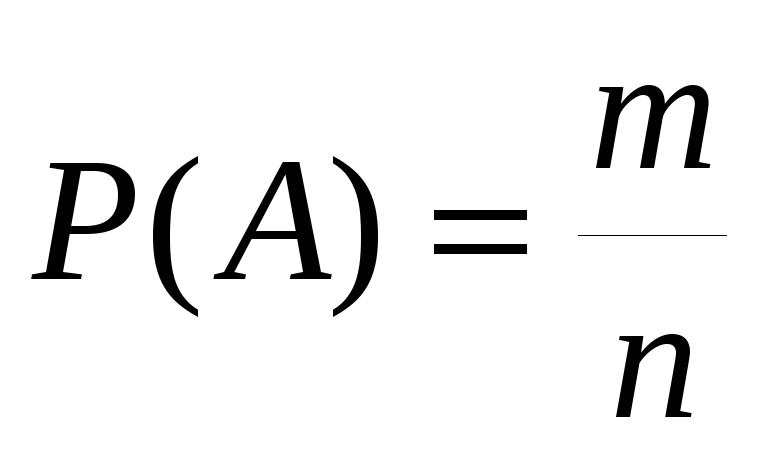 , где
, где
m – число исходов, благоприятствующих событию А;
n – число всех возможных исходов испытания.
Свойства вероятности:
1). Вероятность достоверного события равна 1: 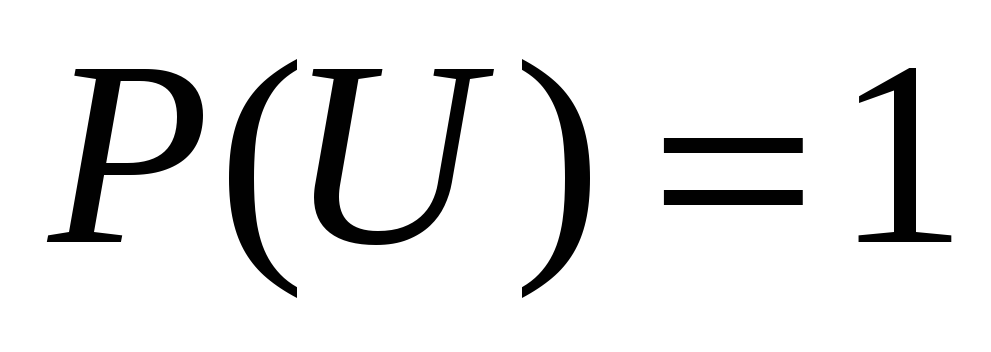 .
.
2). Вероятность невозможного события равна 0: 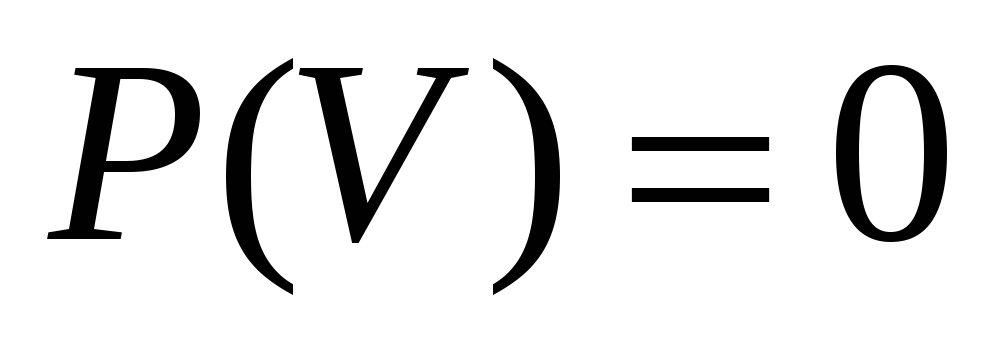
3). Вероятность случайного события есть положительное число, заключенное между нулем и единицей: 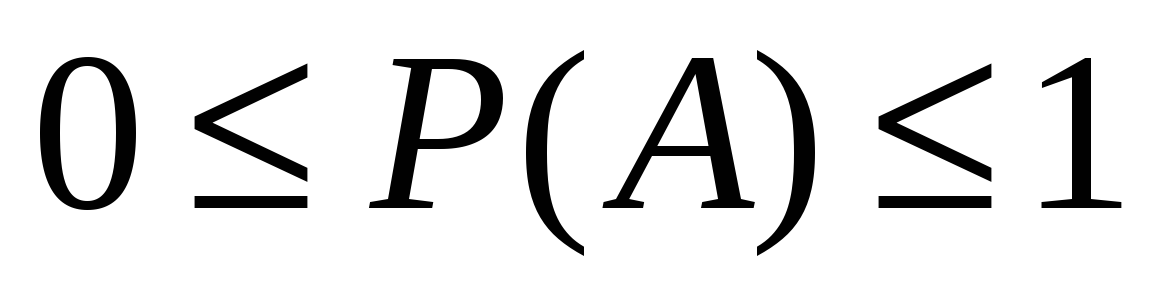 .
.
4). Сумма вероятностей противоположных событий равна 1:
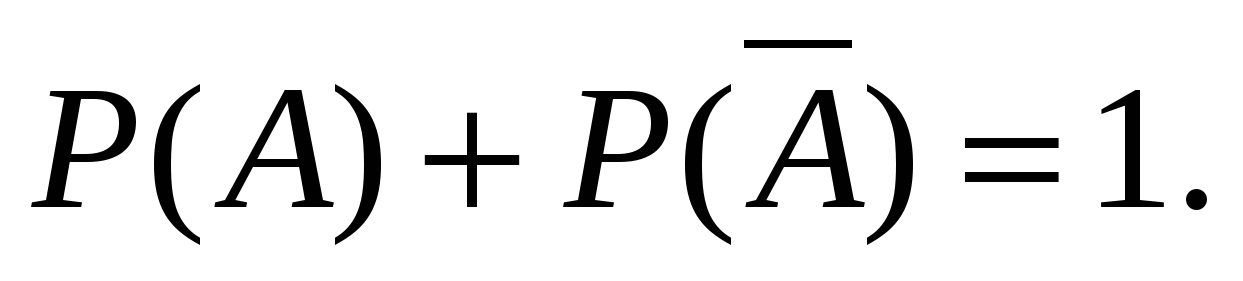
5). Если события А1, А2, …, Аn образуют полную группу попарно несовместных событий, то
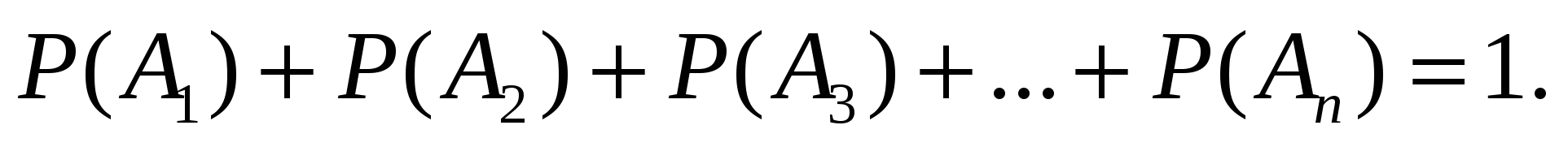
Задача 1. Вероятность выигрыша в лотерею равна 0,034. Какова вероятность проигрыша?
Решение:
Событие A: выигрыш в лотерее.
Событие  : проигрыш в лотерее.
: проигрыш в лотерее.
События A и  являются противоположными, значит,
являются противоположными, значит,
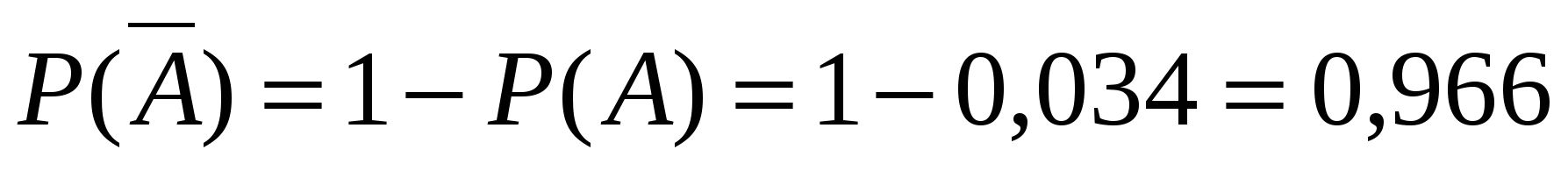 .
.
Ответ: вероятность проигрыша равна 0, 966.
Задача 2. В лотерее из 1000 билетов имеются 200 выигрышных. Вынимают наугад один билет. КВТ, Ч этот билет выигрышный?
Решение.
Событие A: выбран выигрышный билет.
Р (А) = 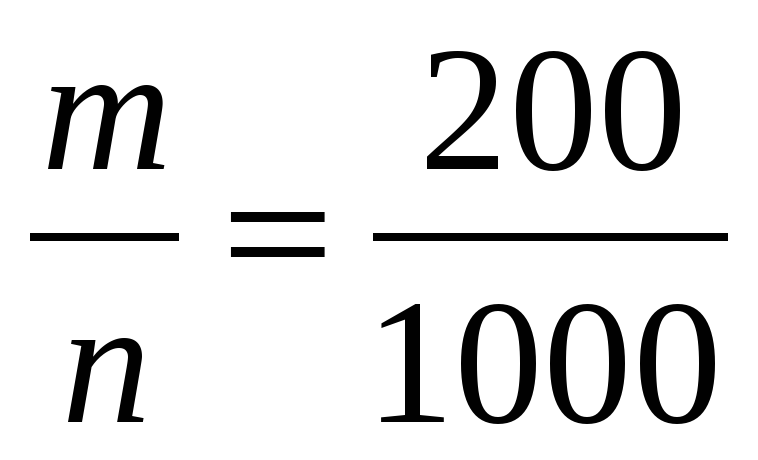 =
= 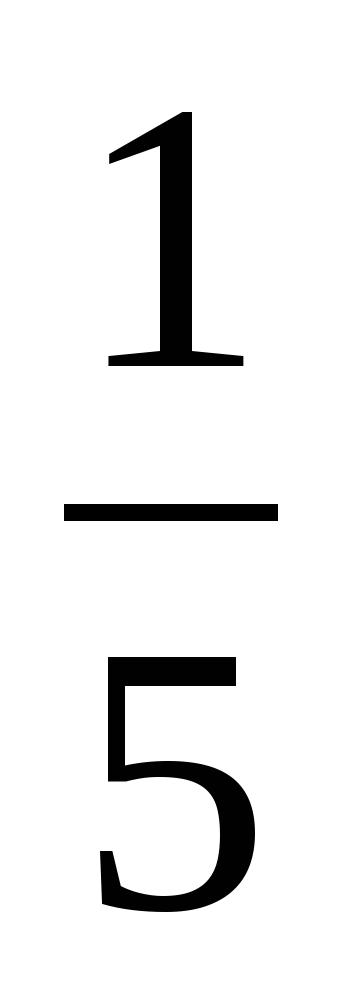 = 0,2.
= 0,2.
Ответ: вероятность выбора выигрышного билета равна 0,2.
Задача 3. Из урны, в которой находятся 10 белых и 3 черных шара, вынимают один шар. КВТ, Ч шар окажется черным.
Решение.
Событие A: выбран чёрный шар.
Р (А) = 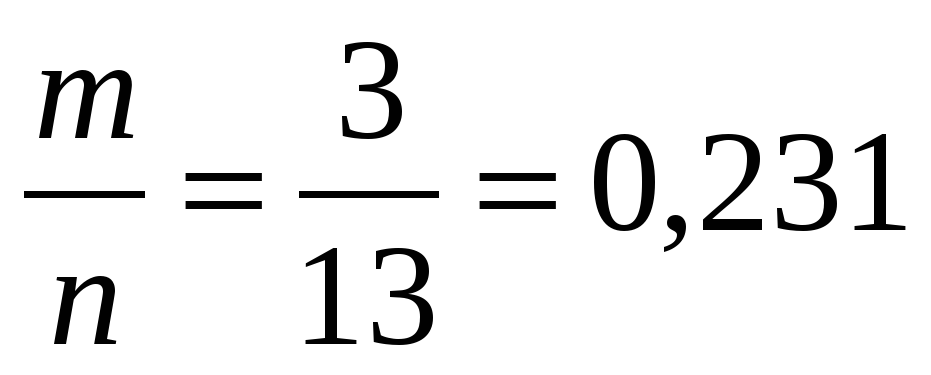 .
.
Ответ: вероятность выбора чёрного шара равна 0,231.
Задача 4. Бросается игральная кость. КВТ, Ч выпадет чётное число очков?
Решение:
Событие А: выпало чётное число очков;
m = (2, 4, 6) = 3;
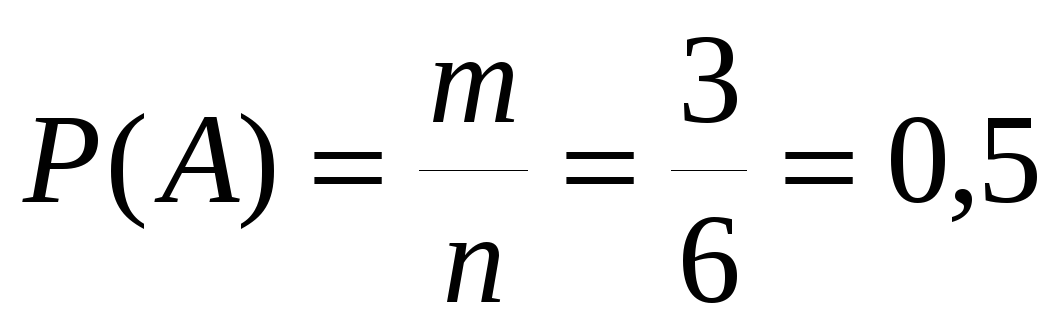 .
.
Ответ: вероятность, что выпадет чётное число очков 0,5.
Задача 5. Бросаются две игральные кости. КВТ, Ч сумма выпавших очков меньше 13? Меньше двух?
Решение:
1. Испытание: бросание двух игральных костей.
2. Исход: на каждой из них выпало любое число очков от 1 до 6;
3. Число всех исходов испытания: n = 6∙6 = 36;
А) 4. Событие А: сумма выпавших очков меньше 13;
5. Число исходов, благоприятствующих событию А: m = 36;
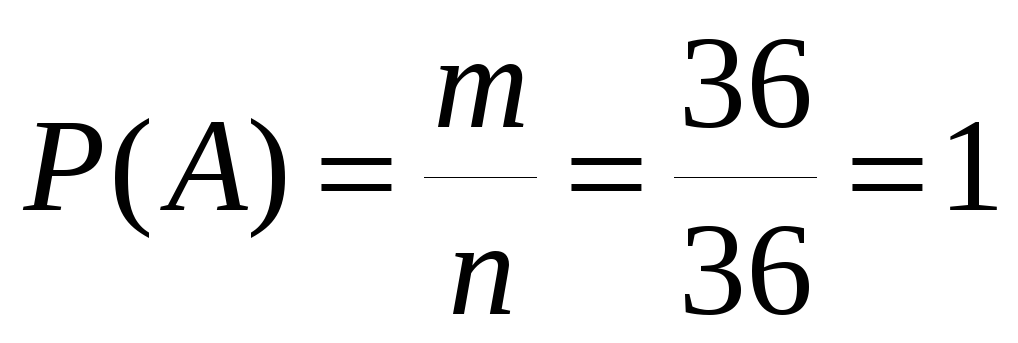 .
.
событие А – достоверное, а его вероятность равна 1.
Б) 4. Событие В: сумма выпавших очков меньше 2;
5. Число исходов, благоприятствующих событию В: m = 0;
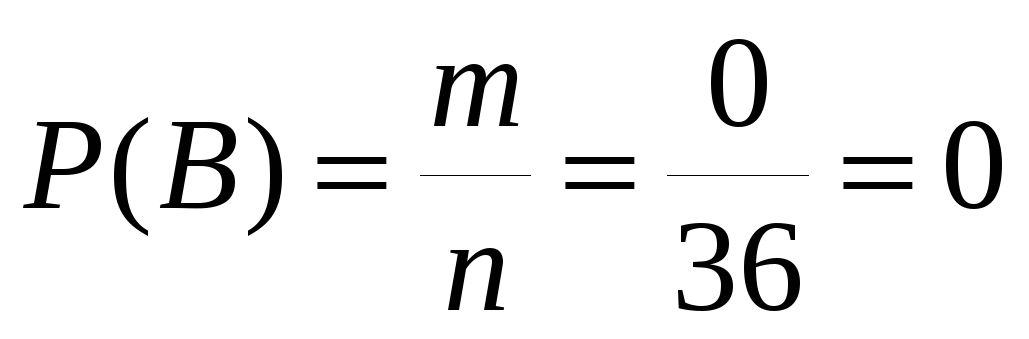 .
.
событие В – невозможное, а его вероятность равна 0.
Ответ: вероятность того, что сумма очков меньше 13 равна 1; вероятность того, что сумма очков меньше 2 равна 0.
При вычислении вероятностей часто применяется комбинаторика.
Задача 6. Из урны, в которой находятся 12 белых и 8 черных шаров, вынимают наудачу два шара. КВТ, Ч оба шара окажутся черными?
Решение.
1. Исход: вынули любые два шара;
2. Число всех исходов испытания: n = 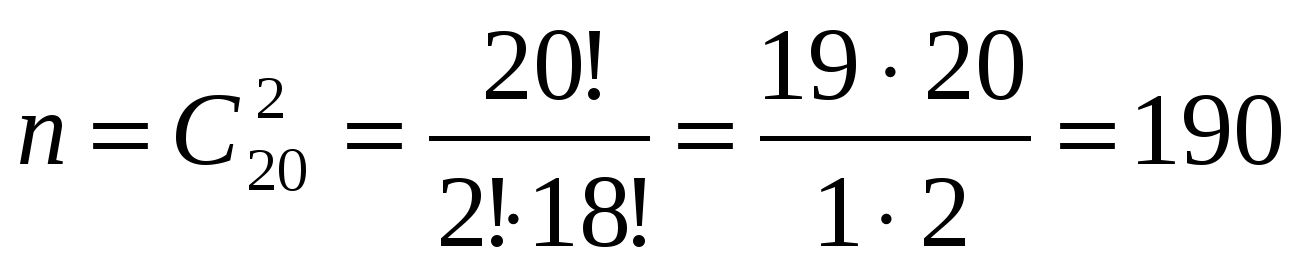 ;
;
3. Событие А: вынули два чёрных шара;
4. Число исходов, благоприятствующих событию А: 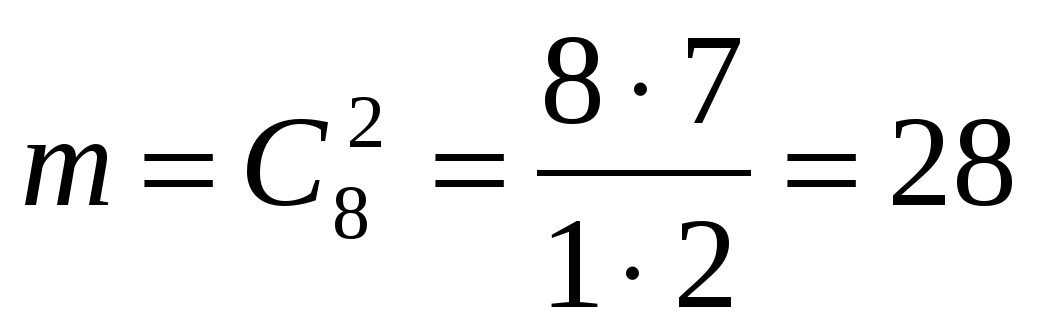 .
.
Р (А) = 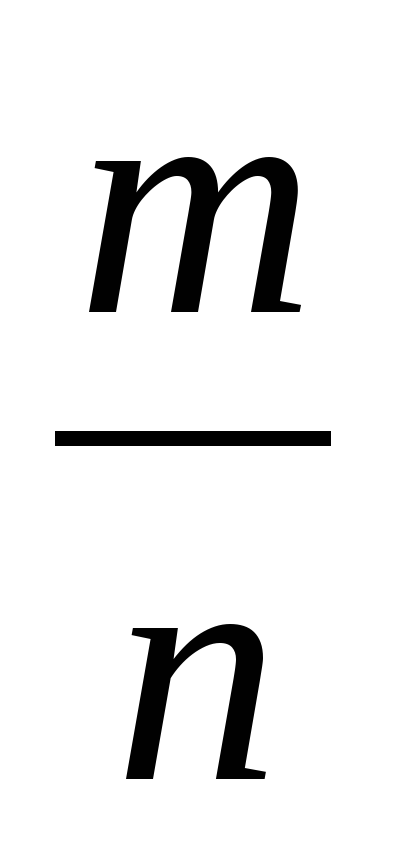 =
= 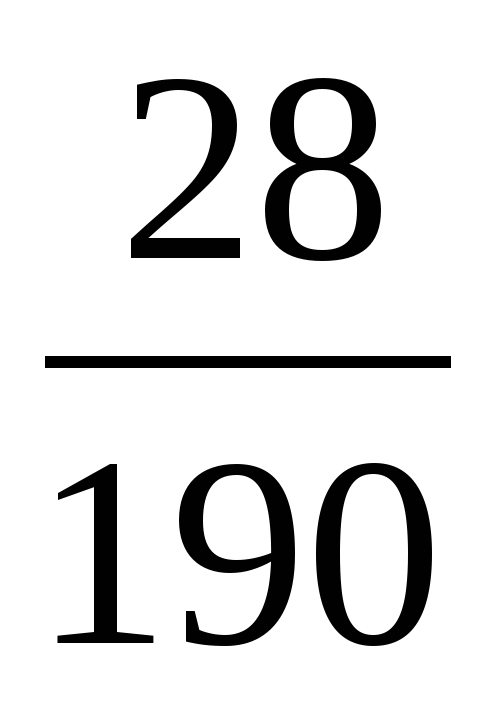 =
= 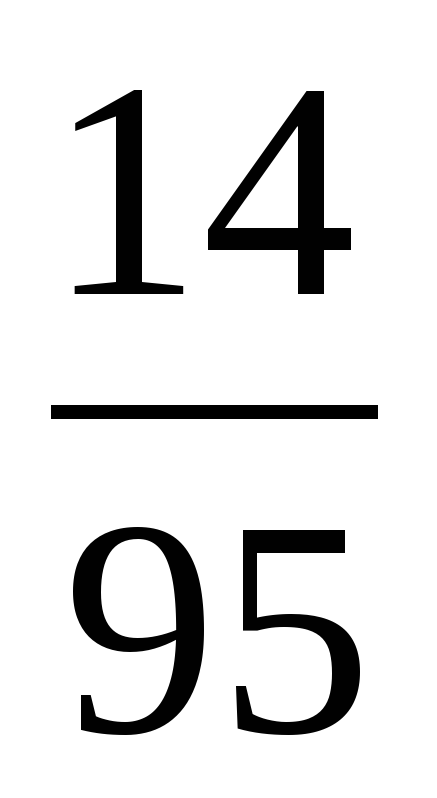 = 0,147.
= 0,147.
Ответ: вероятность того, что вынули два чёрных шара, равна 0,147.
Задача 7. На каждой из 7 одинаковых карточек напечатана одна из следующих букв: Н, О, П, Р, С, Т, У. КВТ, Ч 5 взятых наугад и расположенных в ряд карточках получено слово СПОРТ?
Решение:
1. Исход: получено любое слово;
2. Число всех исходов испытания: n = 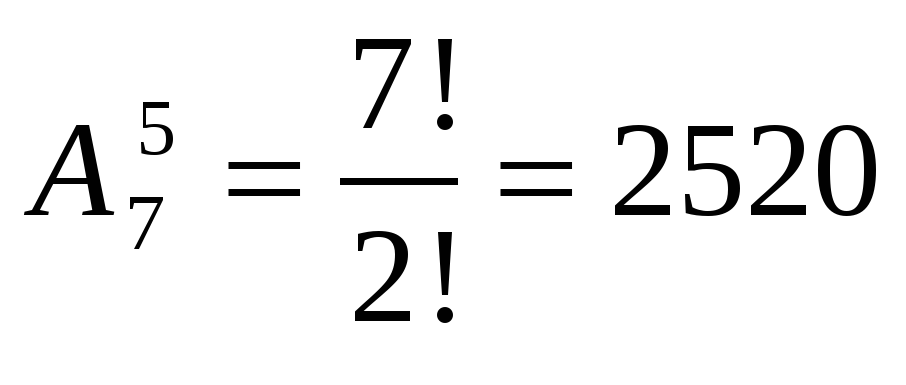 слов может получиться;
слов может получиться;
3. Событие А: получено слово СПОРТ;
4. Число исходов, благоприятствующих событию А: m = 1;
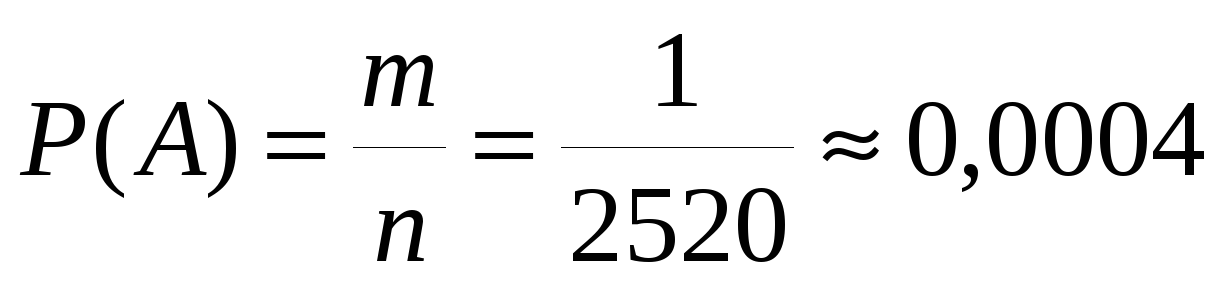 .
.
Ответ: вероятность получения слова «СПОРТ» равна 0,0004.
Задача 8. В партии из 18 деталей находятся 4 бракованных. Наугад выбирают 5 деталей. КВТ, Ч из этих 5 деталей две окажутся бракованными?
Решение.
1. Исход: выбраны любые 5 деталей;
2. Число всех исходов испытания: n = 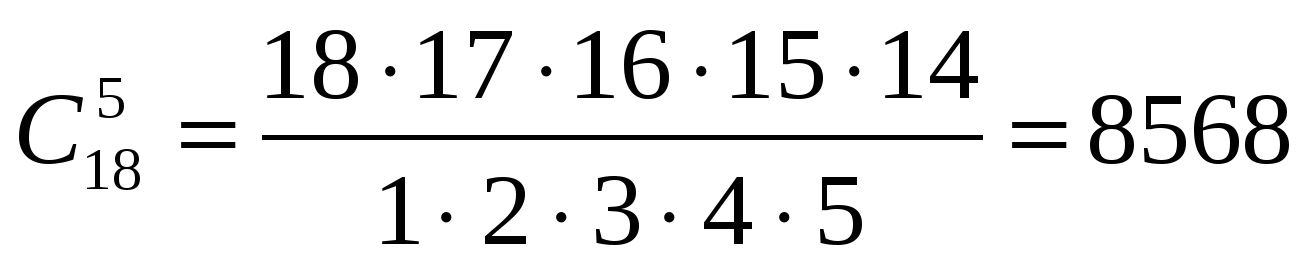 ;
;
3. Событие А: из 5 деталей 2 бракованные;
4. Число исходов, благоприятствующих событию А:
m = 2 браков. и 3 станд. = 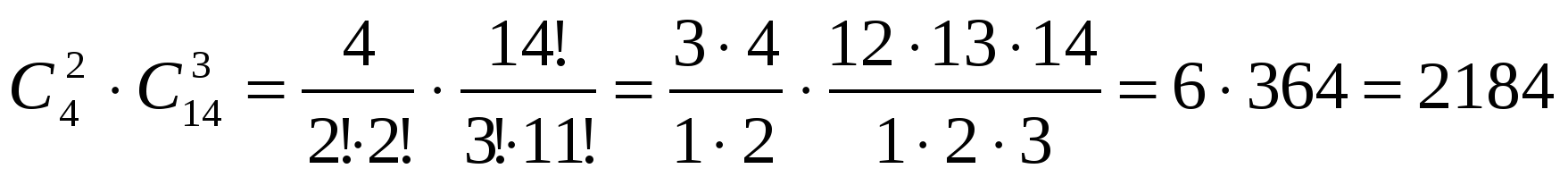 ;
;
Р (А) = = 0,255.
Ответ: вероятность того, что среди 5 деталей 2 бракованные равна 0,255.
3 Порядок выполнения работы:
проработать теоретический материал по теме;
ответить на контрольные вопросы;
получить вариант задания (смотрите Приложение А);
выполнить задание;
оформить отчёт о работе.
4 Контрольные вопросы
Дайте определение события.
Дайте определение случайного события.
Какие события называют достоверными, невозможными, несовместными, совместными, равновозможными?
Какие события называются противоположными? Чему равна вероятность таких событий?
Дайте определение полной системы событий.
Что такое вероятность?
Назовите свойства вероятности.
5 Рекомендации по оформлению отчета по лабораторной работе
Отчет по лабораторной работе выполняется на листах А4 (210 ˟ 291) в соответствии с едиными требованиями ЕСКД.
Отчет по практической работе должен содержать:
вид работы;
точное наименование;
цель;
ход работы;
условие задания (свой вариант задания, смотри в приложении А);
результаты выполнения лабораторной работы;
вывод, в который записать формулу классического определения вероятности.
Литература
Калинина В.Н., Панкин В.Ф. Математическая статистика. – М.: Высшая школа, 1998.
Валуцэ И.И., Дилигул Г.Д. Математика для техникумов. – М.: Наука, 1989.
Алгебра и начала анализа. Часть 2./под ред. Г.Н. Яковлева. – М.: Наука, 1988.
Максимова О.В. Теория вероятностей и математическая статистика. – М.: «Дашков и Ко», 2007.
Корчуганова И.Б. Решение задач на классическое определение вероятности. Методические рекомендации и лабораторная работа по дисциплине «Теория вероятностей и математическая статистика». – Череповец, 2002.
Венцель Е.С., Овчаров Л.А. Задачи и упражнения по теории вероятностей. – М.: ACADEMA, 2005.
Приложение А Варианты заданий
Вариант 1
1). Испытание: бросание монеты:
Событие А1: появление герба;
Событие А2: появление цифры.
Образуют ли полную систему событий события А1 и А2?
2). Испытание: два студента сдают экзамен по теории вероятности.
Событие А: первый студент сдал экзамен.
Событие В: второй студент сдал экзамен.
События А и В являются совместными или несовместными?
3). Событие A: из 6 случайным образом купленных газет не менее 2 газет
окажутся местными. Сколько элементарных событий благоприятствует
событию A? Событию  ?
?
4). Вероятность попадания при одном выстреле равна 0,24. Какова
вероятность промаха при одном выстреле?
5). В коробке находятся 100 лампочек по 100 Вт, 60 – по 60 Вт, 40 – по 25 Вт и 30 – по 15 Вт. Какова вероятность того, что мощность наугад взятой лампочки 25 Вт?
6). Бросаются две игральные кости. Запишите все возможные исходы, и найдите вероятность того, что сумма выпавших очков меньше 7?
7). В классе 17 девочек и 14 мальчиков. Какова вероятность того, что вызваны 2 мальчика?
8).Из 10 карточек «СТАТИСТИКА» разрезанных по буквам наугад берут 5.
Какова вероятность того, что получится слово «ТАКСИ»?
9).В коробке 5 синих, 4 красных и 3 зеленых карандаша. Наудачу вынимают три карандаша. Какова вероятность того, что все они зелёного цвета?
10).Четыре билета на ёлку распределили по жребию между 15 мальчиками и
12 девочками. Какова вероятность того, что билеты достанутся 2 мальчикам и 2 девочкам?
11).В партии из 30 деталей 4 нестандартные. Из партии выбирают для
контроля 5 изделий. Какова вероятность того, что ровно 2 из них стандартные?
12). Из цифр 1, 2, 3, 4, 5 составляют трёхзначные числа без повтора цифр.
Какова вероятность того, что они не кратны 5?
Вариант 2
1). Испытание: два выстрела по мишени;
Событие А1: ни одного попадания;
Событие А2: одно попадание;
Событие А3: два попадания.
Образуют ли полную систему событий события А1, А2, A3?
2). Являются ли равновозможными события?
Опыт: вынимание одной карты из колоды;
Событие В1: появление карты бубен;
Событие В2: появление карты червей;
Событие В3: появление карты крести.
3). Событие A: из корзины, в которой лежат 15 яблок и 10 апельсинов и 6 лимонов, вынимают 4 произвольных фруктов. Сколько элементарных событий благоприятствует событию A? Событию  ?
?
4).Вероятность попадания при одном выстреле равна 0,26. Какова
вероятность промаха при одном выстреле?
5). Какова вероятность того, что выбранное наугад число от 1 до 100 не содержит цифры 6?
6). Бросаются две игральные кости. Запишите все возможные исходы, и найдите вероятность того, что сумма выпавших очков больше 8?
7). В ящике 8 деталей, из которых 4 стандартных. Контролёр берёт на удачу одну за другой 3 детали. Какова вероятность того, что все выбранные детали стандартные.
8). Каждая буква слова «ТОСКА» написана на отдельных карточках. Вынимая последовательно одну за другой, составляется слово из 3 букв. Какова вероятность того, что это слово «КОТ»?
9).В урне 7 белых и 13 чёрных шаров. Вынимают сразу 2 шара. Какова вероятность того, что они оба белые?
10).В коробке конфет 15 с шоколадной начинкой, 12 с помадкой и 18 с
повидлом. Наудачу из коробки вынимают 3 конфеты. Какова вероятность того, что две с шоколадной начинкой и одна с повидлом?
11).Среди 25 студентов группы, в которой 10 девушек, разыгрывается 5
билетов. Какова вероятность того, что среди обладателей билетов окажутся 2 девушки?
12). Из цифр 1, 2, 3, 4, 5 составляют трёхзначные числа без повтора цифр.
Какова вероятность того, что они кратны 5?
Вариант 3
1). Испытание: два выстрела по мишени.
Событие А1: хотя бы одно попадание;
Событие А2: хотя бы один промах.
Образуют ли полную систему событий события А1 и А2?
2). Являются ли равновозможными следующие события?
Опыт: бросание игральной кости.
Событие А1: появление не менее трех очков.
Событие А2: появление не более четырех очков.
3). Событие A: из 5 выстрелов стрелок попал в цель менее 3 раз. Сколько элементарных событий благоприятствует событию A? Событию  ?
?
4). Вероятность попадания при одном выстреле равна 0,29. Какова вероятность промаха при одном выстреле?
5). В ящике 15 белых и 30 чёрных шаров. Наудачу из ящика достают 1 шар.
Какова вероятность того, что шар белый.
6). Бросаются две игральные кости. Запишите все возможные исходы, и найдите вероятность того, что сумма выпавших очков равна 6?
7). В отделе работают 10 инженеров, 5 техников и 3 лаборанта. Среди сотрудников отдела случайным образом отбирают 5 человек для дежурства
в праздничный день. КВТ, Ч все 5 человек окажутся инженерами?
8). Из карточек «Н», «Р», «С», «Л», «Е», «О» наугад выбирают
последовательно четыре и располагают в ряд. Какова вероятность того, что получится слово «СЛОН»?
9).В партии из 20 деталей 3 нестандартные. Из партии выбирают для контроля 4 изделия. КВТ, Ч все 4 изделия будут стандартными?
10).В коробке 5 синих, 4 красных и 3 зеленых карандаша. Наудачу вынимают
3 карандаша. КВТ, Ч вынули 2 красных и один зеленый?
11).В розыгрыше участвуют 18 команд, из них 5 экстра-класса. Из всех команд формируются 2 группы по 9 команд. Какова вероятность того, что в одной
группе окажется 2 команды экстра-класса?
12). Из цифр 1, 2, 3, 4, 5 составляют трёхзначные числа без повтора цифр.
Какова вероятность того, что они нечётные?
Вариант 4 1).Испытание: два выстрела по мишени;
Событие А1: ни одного попадания;
Событие А2: одно попадание.
Образуют ли полную систему событий события А1, А2?
2). Испытание: бросание двух монет;
Событие В1: появление герба на первой монете;
Событие В2: появление цифры на второй монете.
Являются ли несовместными события B1 и B2?
3).Событие A: из 5 выстрелов в цель, стрелок попал чётное число раз. Сколько
элементарных событий благоприятствует событию A? Событию  ?
?
4). Вероятность попадания при одном выстреле равна 0,32. Какова вероятность промаха при одном выстреле?
5). В лотерее из 50 билетов 8 выигрышных. Какова вероятность того, что выбранный наугад билет будет не выигрышным.
6). Бросаются две игральные кости. Запишите все возможные исходы, и найдите вероятность того, что сумма выпавших очков больше 9?
7). На складе имеется 25 подшипников, причём 20 из них изготовлены на
Саратовском ГПЗ. Какова вероятность того, что среди взятых наудачу пяти подшипников, все окажутся Саратовского завода.
8). Десять карточек с буквами А,Д,И,Е,В,О,Р,Ь,М,Т сложены в коробку. Какова вероятность того, что вынимая 5 последовательно одну за другой получится слово «ДВЕРЬ»?
9).Из колоды 36 карт наугад вынимают четыре карты. Какова вероятность того, что это четыре крестовые карты?
10).В партии из 10 деталей 6 дефектных. Какова вероятность того, что из пяти деталей, отобранных для контроля 3 дефектных?
11).В урне 4 белых и 7 черных шаров. Вынимают 5 из них. Какова вероятность того, что два – белые, 3 - черные?
12). Из цифр 1, 2, 3, 4, 5 составляют трёхзначные числа без повтора цифр.
Какова вероятность того, что они чётные?
Вариант 5
1). Испытание: выбор двух шаров из урны, в которой находятся 3 белых и 4 чёрных шара:
Событие А1: появление белого шара;
Событие А2: появление чёрного шара;
Событие А3: появление одного белого и одного чёрного шара.
Образуют ли полную систему событий события А1 и А2?
2). Испытание: бросание игрального кубика.
Событие А: выпадение шестёрки.
Событие В: выпадение числа очков не менее четырёх.
События А и В являются совместными или несовместными?
3). Событие A: из 6 выстрелов в цель, стрелок попал нечётное число раз. Сколько элементарных событий благоприятствует событию A? Событию  ?
?
4). Вероятность попадания при одном выстреле равна 0,34. Какова вероятность промаха при одном выстреле?
5). Из колоды в 36 карт извлекают одну. Какова вероятность того, что извлечена карта бубновой масти?
6). Бросаются две игральные кости. Запишите все возможные исходы, и найдите вероятность того, что сумма выпавших очков равна 7?
7). В урне 4 белых и 7 черных шаров. Наугад взяты два. Какова вероятность того, что оба белые?
8). Из карточек «Н», «Р», «С», «Л», «Ё», «О» наугад выбирают последовательно четыре и располагают в ряд. Какова вероятность того, что получится слово
«ОСЁЛ»?
9).Из колоды 36 карт наугад вынимают четыре карты. Какова вероятность того, что это четыре чёрные карты?
10).В коробке конфет 15 с шоколадной начинкой, 12 с помадкой и 18 с
повидлом. Наудачу из коробки вынимают 5 конфет. КВТ, Ч две с помадкой и три с повидлом.
11).В партии из 18 деталей имеется 10 стандартных. КВТ, Ч среди 6 взятых
наугад деталей 4 стандартных?
12). Из цифр 1, 2, 3, 4, 5, 6 составляют четырёхзначные числа без повтора цифр. Какова вероятность того, что они чётные?
Вариант 6
1). Испытание: бросание двух монет;
Событие С1: появление двух гербов;
Событие С2: появление двух цифр;
Событие С3: появление одного герба и одной цифры.
Образуют ли полную систему событий события C1, C2, C3?
2). Испытание: стрелок производит один выстрел по мишени.
Событие А: стрелок попал в мишень.
Событие В: стрелок не попал в мишень.
Тогда событие А и В являются несовместными или совместными?
3). Событие A: из 7 случайным образом купленных открыток не менее 3
окажутся новогодними. Сколько элементарных событий благоприятствует
событию A? Событию  ?
?
4). Вероятность попадания при одном выстреле равна 0,37. Какова вероятность промаха при одном выстреле?
5). Из ящика наугад берут 1 лампочку. Какова вероятность того, что она стандартная, если в ящике 40 лампочек, из них 7 бракованных?
6). Бросаются две игральные кости. Запишите все возможные исходы, и найдите вероятность того, что произведение выпавших очков равна 12?
7). В коробке имеются 30 лотерейных билетов, из которых 26 без выигрышей.
Наугад вынимают одновременно 3 билета. Какова вероятность того, что все три билета будут выигрышными.
8). Из шести карточек «К», «Р», «С», «Л», «Е», «О» наугад выбирают одну за другой, и располагают в ряд. Какова вероятность того, что получится слово «КРЕСЛО»?
9).Из колоды 36 карт наугад вынимают две карты. Какова вероятность того, что это две дамы?
10).В урне находятся 12 белых и 8 черных шаров. Какова вероятность того, что среди наугад вынутых 7 шаров 4 будут черными?
11).На полке лежат 15 учебников, из них 7 - по математике. Студент берёт 5
учебников. Какова вероятность того, что среди 5 учебников 3 по математике?
12). Из цифр 1, 2, 3, 4, 5, 6 составляют четырёхзначные числа без повтора цифр. Какова вероятность того, что они нечётные?
Вариант 7
1). Испытание: подбрасывание игральной кости;
Событие А1: появление не более двух очков;
Событие А2: появление трех или четырех очков;
Событие А3: появление не менее пяти очков.
Образуют ли полную систему событий события А1, А2, A3?
2). Испытание: подбрасывается игральная кость.
Событие А: выпало число очков не менее 20.
Тогда событие А является невозможным, достоверным, или случайным.
3). Событие A: появление белого шара при вынимании одного шара из урны, в которой 2 белых, 3 черных и 4 красных шара. Сколько элементарных событий благоприятствует событию A? Событию  ?
?
4). Вероятность попадания при одном выстреле равна 0,41. Какова вероятность промаха при одном выстреле?
5). Из колоды в 36 карт наугад выбирают одну. Какова вероятность того, что карта семёрка?
6). Бросаются две игральные кости. Запишите все возможные исходы, и найдите вероятность того, что сумма выпавших очков меньше 6?
7). В барабане револьвера 7 гнезд, из них в пяти патроны. При его вращении
против ствола появляется одно из гнезд. Какова вероятность того, что при нажатии спускового крючка 2 раза выстрелы произойдут?
8). Из карточек «Т», «Р», «С», «Л», «Ё», «О» наугад выбирают последовательно четыре, и располагают в ряд. Какова вероятность того, что получится слово «РОСТ»?
9).На базу привезли 11 ящиков яблок I сорта и 7 ящиков яблок II сорта.
Наугад выбирают два ящика. Какова вероятность того, что оба ящика с яблоками II сорта?
10).В партии из 18 деталей находится 4 бракованных. Наугад выбирается 7
деталей. Какова вероятность того, что из 7 деталей три окажутся бракованными.
11).В цехе работают 6 мужчин и 4 женщины, По табельным номерам наудачу отобраны 7 человек. Какова вероятность того, что среди отобранных лиц окажется 3 женщины.
12). Из цифр 1, 2, 3, 4, 5, 6 составляют трёхзначные числа без повтора цифр.
Какова вероятность того, что они чётные?
Вариант 8
1). Испытание: три выстрела по мишени;
Событие А1: хотя бы одно попадание;
Событие А2: хотя бы один промах.
Образуют ли полную систему событий события А1 и А2?
2). Являются ли равновозможными следующие события?
Опыт- бросание игральной кости.
Событие А1: появление не менее трех очков.
Событие А2: появление не более четырех очков.
3). Пусть событие A состоит в изъятии туза из колоды в 36 карт. Сколько
элементарных событий благоприятствуют событию A, событию  ?
?
4). Вероятность попадания при одном выстреле равна 0,43. Какова вероятность
промаха при одном выстреле?
5). На карточках написаны числа от 10 до 22. Наугад, не глядя, берут одну.
Какова вероятность того, что на ней будет нечётное число.
6). Бросаются две игральные кости. Запишите все возможные исходы, и найдите вероятность того, что произведение выпавших очков равна 4?
7). В классе 12 девочек и 13 мальчиков. Наугад вызываются три ученика. Какова вероятность того, что вызваны 3 девочки?
8). Каждая буква слова «ТРАНСПОРТЕР» написана на отдельных карточках. Вынимая одну за другой, составляется слово из 9 букв. Какова вероятность того, что это слово «ТРАНСПОРТ»?
9).В партии из 20 изделий 3 нестандартных. Из партии выбирают для
контроля 5 изделий. Какова вероятность того, что среди пяти изделий три стандартные?
10).В отделе работают 10 инженеров, 5 техников и 3 лаборанта. Среди
сотрудников отдела случайным образом отбирают 5 человек для дежурства в праздничный день. Какова вероятность того, что 3 человека окажутся техниками, а 2 – лаборанта.
11).В ящике 15 шаров, из которых 5 голубых и 10 красных. Наугад выбирают
6 шаров. Какова вероятность того, что среди вынутых шаров 2 голубых?
12).Из цифр 1, 2, 3, 4, 5, 6 составляют трёхзначные числа без повтора цифр.
Какова вероятность того, что все цифры у них чётные?
Вариант 9
1). Испытание: бросание двух монет.
Событие А1: появление двух гербов;
Событие А2- появление двух цифр.
Образуют ли полную систему событий события А1 и А2?
2). Испытание: два выстрела по мишени.
Событие A: есть хотя бы одно попадание.
Событие B: ни одного попадания.
События А и В являются совместными или несовместными?
3). Событие A: из коробки, в которой 12 фломастеров, 6 карандашей и 4 ручки, вынимают 3 предмета? Сколько элементарных событий благоприятствует событию A? Событию  ?
?
4). Вероятность попадания при одном выстреле равна 0,53. Какова вероятность
промаха при одном выстреле?
5). Из колоды в 36 карт наугад выбирают одну. Какова вероятность того, что это чёрный туз?
6). Бросаются две игральные кости. Запишите все возможные исходы, и найдите вероятность того, что сумма выпавших очков равна 5?
7). В урне 7 белых и 6 черных шаров. Какова вероятность того, что взятые наугад 3 шара будут чёрными?
8). Дано шесть карточек с буквами Н, М, И, Я, Л, О. Какова вероятность того, что получится слово ЛОМ, если наугад одна за другой выбираются три
карточки.
9). В партии из 18 изделий 5 нестандартных. Из партии выбирают для контроля 6 изделий. Какова вероятность того, что среди шести изделий три нестандартные?
10).Среди 25 студентов группы, в которой 10 девушек, разыгрывается 5
билетов. Какова вероятность того, что среди обладателей билетов окажутся 2 девушки.
11).В лотерее из 30 билетов 10 выигрышных. Некто купил 4 билета. Какова вероятность того, что два из них выигрышных?
12). Из цифр 0, 2, 3, 4, 5, 6 составляют трёхзначные числа без повтора цифр.
Какова вероятность того, что они не кратны 5?
Вариант 10
1). Испытание: выбор двух шаров из урны, в которой находятся 4 белых и 5 чёрных шара:
Событие А1: появление белого шара;
Событие А2: появление чёрного шара;
Образуют ли полную систему событий события А1 и А2?
2). Испытание: подбрасывается игральная кость.
Событие А: выпало 10 очков.
Событие А является невозможным событием, или случайным событием,
или достоверным.
3). Событие A: в серии из 10 подбрасываний монеты орёл выпадет более 5 раз. Сколько элементарных событий благоприятствует событию A? Событию  ?
?
4). Вероятность попадания при одном выстреле равна 0,57. Какова вероятность промаха при одном выстреле?
5). Из колоды в 36 карт наугад выбирают одну. Какова вероятность того, что эта карта «шестерка» красная?
6). Бросаются две игральные кости. Запишите все возможные исходы, и найдите вероятность того, что произведение выпавших очков больше 15?
7). В ящике имеется 20 деталей, из которых 15 окрашены. Наудачу извлечены 4 детали. Какова вероятность того, что извлечённые детали окажутся окрашенными.
8). Какова вероятность того, что из букв Н, А, А, Н, С, А получится слово «АНАНАС», вынимая их одна за другой буквы наугад и располагая в ряд?
9).В партии из 28 изделий 9 нестандартных. Из партии выбирают для контроля 7 изделий. КВТ, Ч все 7 изделий стандартные?
10).В урне 9 белых и 11 черных шаров. Вынимают 5 из них. Какова вероятность того, что два - белые, 3-черные?
11).В группе 20 студентов, среди которых 12 отличников. По списку наудачу отобраны 8 студентов. Какова вероятность того, что среди отобранных студентов 5 отличников.
12). Из цифр 1, 2, 3, 4 составляют трёхзначные числа без повтора цифр.
Какова вероятность того, что они нечётные?
Вариант 11
1). Испытание: два выстрела по мишени;
Событие А1: одно попадание;
Событие А2: два попадания.
Образуют ли полную систему событий события А1, А2?
2). Испытание: бросание игрального кубика.
Событие А: выпадение единицы.
Событие В: выпадение числа очков не менее четырёх.
События А и В являются совместными или несовместными?
3). Событие A: появление черного шара при вынимании одного шара из урны, в которой 4 белых, 2 черных и 5 красных шара. Сколько элементарных событий благоприятствует событию A? Событию  ?
?
4). Вероятность попадания при одном выстреле равна 0,25. Какова вероятность
промаха при одном выстреле?
5). На карточках написаны однозначные числа от 9 до 29. Наугад, не глядя, берут одну. Какова вероятность того, что на ней будет чётное число.
6). Бросаются две игральные кости. Запишите все возможные исходы, и найдите вероятность того, что произведение выпавших очков меньше 9?
7). В мастерскую для ремонта поступило 15 телевизоров. Известно, что 6 из них нуждаются в общей регулировке. Мастер берет первые попавшиеся 5 телевизоров. Какова вероятность того, что они нуждаются в общей настройке?
8). Из разрезной азбуки (33 буквы) вынимаются одна за другой 4 карточки. Какова вероятность того, что получится слово «СТОЛ»?
9). В коробке конфет 15 с шоколадной начинкой, 12 с помадкой и 18 с повидлом. Наудачу из коробки вынимают 3 конфеты. Какова вероятность того, что две с шоколадной начинкой и одна с повидлом?
10). В урне 12 белых и 13 черных шаров. Вынимают 6 из них. Какова вероятность того, что все 6 шаров - чёрные?
11). С помощью наблюдений установлено, что в некоторой местности в сентябре в среднем бывает 18 дождливых дней. Какова вероятность того, что из наугад взятых в этом месяце 7-ми дней 3 будут дождливыми?
12). Из цифр 1, 2, 3, 4 составляют трёхзначные числа без повтора цифр.
Какова вероятность того, что они чётные?
Вариант 12
1). Испытание: вынимание карты из колоды.
Событие А1: появление карты червонной масти;
Событие А2: появление карты бубновой масти;
Событие А3: появление карты трефовой масти;
Образуют ли полную систему событий события А1, А2, A3?
2). Являются ли равновозможными следующие события?
Опыт: бросание двух монет.
Событие А1: появление двух гербов.
Событие А2: появление двух цифр.
Событие A3: появление одного герба и одной цифры.
3). Событие A: из 6 случайным образом купленных тетрадей не менее 4 тетрадей
окажутся по 18 листов. Сколько элементарных событий благоприятствует
событию A? Событию  ?
?
4). Вероятность попадания при одном выстреле равна 0,64. Какова вероятность
промаха при одном выстреле?
5). В ящике имеется 60 одинаковых деталей, из них 5 окрашенных. Наудачу
вынимают одну деталь. Какова вероятность того, что извлеченная деталь
окажется окрашенной.
6). Бросаются две игральные кости. Запишите все возможные исходы, и найдите вероятность того, что сумма выпавших очков равна 9?
7). Среди лотерейных билетов 13 выигрышных и 10 билетов без выигрыша. Взяли 7 билетов. Какова вероятность того, что все они выигрышные?
8). Из пяти карточек А, Б, В, Г, Д наугад выбирают одну за другой три и располагают в ряд. Какова вероятность того, что получится слово «ДВА»?
9). В коробке 8 синих мелков, 6 красных и 4 зеленых мелков. Наудачу вынимают четыре мелка. Какова вероятность того, что все они синего цвета?
10). В классе 12 мальчиков и 18 девочек. Нужно выбрать делегацию из трех человек. Какова вероятность того, что выбраны две девочки и один мальчик.
11). В урне 7 белых и 13 черных шаров. Вынимают 5 из них. Какова вероятность того, что все 5 шаров - белые?
12). Из цифр 0, 1, 2, 3, 4, 5 составляют четырёхзначные числа без повтора цифр. Какова вероятность того, что они кратны 5?
Вариант 13
1). Испытание: вынимание карты из колоды.
Событие А1: появление карты красной масти;
Событие А2: появление карты чёрной масти.
Образуют ли полную систему событий события А1 и А2?
2). Испытание: бросание игрального кубика.
Событие А: выпадение шестёрки.
Событие В: выпадение чётного числа очков.
События А и В являются совместными или несовместными?
3). Событие A: из корзины, в которой лежат 6 яблок и 7 апельсинов и 3 лимона, вынимают 3 произвольных фруктов. Сколько элементарных событий благоприятствует событию A? Событию  ?
?
4). Вероятность попадания при одном выстреле равна 0,38. Какова
вероятность промаха при одном выстреле?
5). Из ящика наугад берут 1 лампочку. Какова вероятность того, что она стандартная, если в ящике 40 лампочек, из них 7 бракованных?
6). Бросаются две игральные кости. Запишите все возможные исходы, и найдите вероятность того, что произведение выпавших очков больше 20?
7). Из полной колоды карт (36 листов) наугад вытягиваются 2 карты. Какова вероятность того, что обе бубновые?
8). Дано пять карточек с буквами Н, М, И, Я, Ч. Какова вероятность того, что
получится слово МЯЧ, если наугад одна за другой выбираются три
карточки.
9). К концу дня в магазине осталось 12 арбузов, из которых 7 спелых. Покупатель выбирает два арбуза. Какова вероятность, что оба арбуза спелые?
10). Среди студентов, из которых 10 девушек, разыгрываются 4 билета, причем каждый может выиграть только один билет. Найти вероятность того, что среди обладателей билета окажутся три юноши и одна девушка.
11). Известно, что среди 12 изделий верхней одежды имеются 5 не прошедших
контроль качества. Какова вероятность при случайном безвозвратном отборе
6 изделий обнаружить среди них 2 не прошедших контроль.
12). Из цифр 1, 2, 3, 4, 5 составляют пятизначные числа без повтора цифр.
Какова вероятность того, что они чётные?
Вариант 14
1). Испытание: два выстрела по мишени.
Событие А1: хотя бы одно попадание;
Событие А2: один промах.
Образуют ли полную систему событий события А1 и А2?
2). Являются ли равновозможными события?
Опыт: бросание двух монет.
Событие С1: появление двух гербов;
Событие С2: появление двух цифр;
Событие С3: появление одного герба и одной цифры.
3). Событие A: в серии из 8 подбрасываний монеты орёл выпадет более 4 раз. Сколько элементарных событий благоприятствует событию A? Событию  ?
?
4). Вероятность попадания при одном выстреле равна 0,44. Какова
вероятность промаха при одном выстреле?
5). В лотерее из 45 билетов 35 без выигрыша. Какова вероятность того, что выбранный наугад билет будет выигрышным.
6). Бросаются две игральные кости. Запишите все возможные исходы, и найдите вероятность того, что сумма выпавших очков равна 5?
7). В партии, в которой 26 деталей без дефектов и 4 с дефектами, берут наудачу 4 детали. Чему равна вероятность того, что все четыре детали без дефектов.
8). Из семи карточек А, Г, С, К, Е, В, Н наугад выбирают одну за другой пять и располагают в ряд. Какова вероятность того, что получится слово «ВЕСНА»?
9). В вазе с цветами 11 гвоздик: 7 белых и 4 красных. Из вазы наугад вынимают 2 цветка. Какова вероятность того, что эти цветки оба белые.
10). В урне 5 белых и 11 черных шаров. Вынимают 5 из них. Какова вероятность того, что вынули два белых шара, 3 - черных?
11). В компания работают 20 сотрудников, из которых 8 женщин. Для интервью выбирают 6 сотрудников. Определить вероятность того, что среди них будет 2
женщины.
12). Из цифр 0, 1, 2, 3, 4, 5 составляют четырёхзначные числа без повтора цифр. Какова вероятность того, что они не кратны 5?
Вариант 15
1). Испытание: три выстрела по мишени.
Событие А1: одно попадание;
Событие А2: два попадания;
Событие A3: три попадания.
Образуют ли полную систему событий события А1 и А2?
2). Испытание: вынимание двух карт из колоды;
Событие А1: появление двух черных карт;
Событие А2: появление туза; А3-появление дамы.
Являются ли несовместными события A1 и A2?
3). Событие A: появление красного шара при вынимании одного шара из урны, в которой 5 белых, 3 черных и 2 красных шара. Сколько элементарных событий благоприятствует событию A? Событию  ?
?
4). Вероятность попадания при одном выстреле равна 0,72. Какова
вероятность промаха при одном выстреле?
5). Из колоды в 36 карт наугад выбирают одну. Какова вероятность того, что эта карта крестовой масти?
6). Бросаются две игральные кости. Запишите все возможные исходы, и найдите вероятность того, что произведение выпавших очков меньше 8?
7). В барабане револьвера 7 гнезд, из них в четырёх патроны. При его вращении
против ствола появляется одно из гнезд. Какова вероятность того, что при нажатии спускового крючка 3 раза выстрелы произойдут?
8). Из букв С, Т, Е, Н, К, А составляется слово, вынимая их последовательно и располагая в ряд. Какова вероятность того, что получится слово « ТАНК»?
9). В партии из 24 деталей 6 нестандартные. Из партии выбирают для контроля 4 изделия. КВТ, Ч все 4 изделия будут стандартными?
10). В вазе с цветами 13 гвоздик: 5 белых и 8 красных. Из вазы наугад вынимают 5 цветков. Какова вероятность того, что вынули 3 красных и два белых цветка?
11). Шесть билетов на ёлку распределили по жребию между 16 мальчиками и
10 девочками. Какова вероятность того, что билеты достанутся 2 мальчикам и 4 девочкам?
12). Из цифр 1, 2, 3, 4, 5 составляют пятизначные числа без повтора цифр.
Какова вероятность того, что они нечётные?
22


























