Решение задач на закон сохранения импульса

Решение задач

«Закон сохранения импульса»

Цель урока:

• Научится применять теоретические знания при решении задач на закон сохранения импульса.
• Рассмотреть примеры задач которые могут быть на ОГЭ по физике
• Проверить уровень усвоения тем «Импульс тела» и «Закон сохранения импульса тел»

Проверяем домашнее задание

• Величина, равная ________________ массы тела на его скорость, называется ______________________________.
• Вектор скорости и импульса движущегося тела имеют __________ направление
• За единицу импульса принимают _____________.
• Если два или несколько тел взаимодействуют только между собой, то эти тела образуют ___________________.
• Закон _______________________ заключается в том, что векторная сумма импульсов тел, образующих замкнутую систему, _________________ с течением времени при любых движениях и взаимодействиях этих тел.
• Для замкнутой системы, состоящей из двух тел, закон сохранения импульса записывается в таком виде ________________________________________.
• Поясните, что означает каждый символ в этом уравнении:_____________________________________________

Проверяем

• Величина, равная произведению массы тела на его скорость, называется импульсом тела
• Вектор скорости и импульса движущегося тела имеют одинаковое направление
• За единицу импульса принимают
• Если два или несколько тел взаимодействуют только между собой, то эти тела образуют замкнутую систему
• Закон сохранения импульса заключается в том, что векторная сумма импульсов тел, образующих замкнутую систему, не меняется с течением времени при любых движениях и взаимодействиях этих тел
• Для замкнутой системы, состоящей из двух тел, закон сохранения импульса записывается в таком виде Р / 1 +Р / 2 =Р 1 +Р 2 или m 1 V / 1 +m 2 V / 2 =m 1 V 1 +m 2 V 2

Решение задач

Задача № 1

Задача № 2

Задача № 3

Домашнее задание

§ 21, 23

Спасибо

за

урок !

Продолжим повторение теории!

Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела

Теорема о кинетической энергии тела: работа приложенной к телу равнодействующей силы равна изменению его кинетической энергии

A = E k2  – Е k1

Потенциальная энергия тела в поле силы тяжести равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень

E p  = mgh

Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией

Продолжим повторение теории!

Закон сохранения энергии в механических процессах:

Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной

А – кинетическая энергия шара;

В – потенциальная энергия шара;

С – полная механическая энергия шара.

Рассмотрим другие примеры

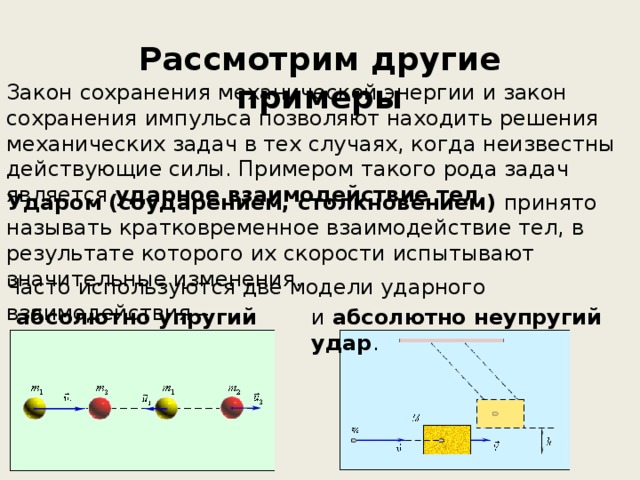
Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда неизвестны действующие силы. Примером такого рода задач является ударное взаимодействие тел.

Ударом (соударением, столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения.

Часто используются две модели ударного взаимодействия –

и абсолютно неупругий удар .

абсолютно упругий удар

Образовательный портал «Мой университет» - www.moi-universitet.ru

Факультет «Реформа образования» - www . edu - reforma . ru

Неупругие и упругие соударения

Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.

Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел.

Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара.

Рассмотрим пример

На основе законов механики математически точно описывается «поведение» бильярдных шаров, столкновения которых друг с другом и со стенками бильярдного стола можно считать абсолютно упругими.

При этом соударения могут быть центральными и нецентральными

Центральное соударение

Нецентральное соударение

Переходим к практике

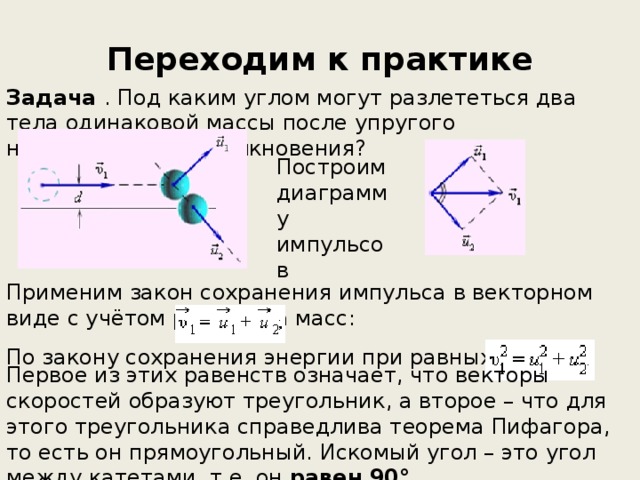
Задача . Под каким углом могут разлететься два тела одинаковой массы после упругого нецентрального столкновения?

Построим диаграмму импульсов

Применим закон сохранения импульса в векторном виде с учётом равенства масс:

По закону сохранения энергии при равных массах:

Первое из этих равенств означает, что векторы скоростей образуют треугольник, а второе – что для этого треугольника справедлива теорема Пифагора, то есть он прямоугольный. Искомый угол – это угол между катетами, т.е. он равен 90° .

Повторим теорию!

для упругого взаимодействия

для неупругого взаимодействия