Решение задач по теме пирамида.

МОУ «Гимназия» г.Черногорск

Маркелова Светлана Валериевна

В правильной четырехугольной пирамиде сторона основания равна 8 см, угол между боковым ребром и плоскостью основания равен 30 ◦ . Найдите высоту пирамиды, боковое ребро, угол между плоскостью основания и боковой гранью, двугранный угол при боковом ребре, площадь полной поверхности пирамиды.

В правильной треугольной пирамиде сторона основания равна 6 см, высота 12 см. Найдите боковое ребро пирамиды, угол между боковым ребром и плоскостью основания пирамиды, угол между боковой гранью и основанием пирамиды, двугранный угол при боковом ребре, площадь полной поверхности.

Основанием пирамиды является равнобедренный треугольник с углом 120 ° . Боковые ребра образуют с плоскостью основания углы по 30 ° . Высота равна 6 см. Найдите площадь полной поверхности пирамиды.

Основанием пирамиды является треугольник со сторонами 12 см, 10 см и 10 см. Каждая боковая грань наклонена к основанию под углом 45°. Найдите площадь боковой поверхности пирамиды.

Основанием пирамиды является прямоугольник, диагональ которого равна 8 см. Плоскости двух боковых граней перпендикулярны к плоскости основания, а две другие боковые грани образуют с основанием углы в 30 ◦ и 45 ◦ . Найдите площадь поверхности пирамиды.

В правильной усечённой четырёхугольной пирамиде стороны оснований 6 см и 10 см. Плоский угол боковой грани 45°. Найти площадь полной поверхности пирамиды.

В правильной треугольной усеченной пирамиде стороны основания 4 и 8, а площадь сечения, проходящего через боковое ребро и середину противоположной стороны основания, равна 6 . Найти площадь полной поверхности пирамиды.

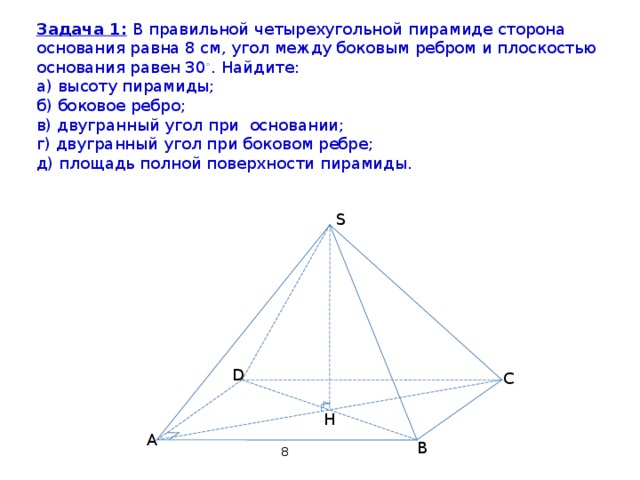
Задача 1: В правильной четырехугольной пирамиде сторона основания равна 8 см, угол между боковым ребром и плоскостью основания равен 30 ◦ . Найдите:

а) высоту пирамиды;

б) боковое ребро;

в) двугранный угол при основании;

г) двугранный угол при боковом ребре;

д) площадь полной поверхности пирамиды.

S

D

C

H

A

B

8

S

D

C

H

30°

A

B

8

8

Н S =

S

D

C

H

30°

A

B

8

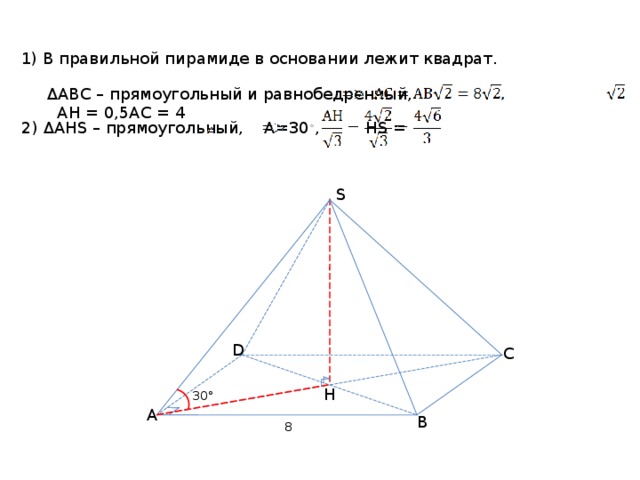
1) В правильной пирамиде в основании лежит квадрат.

Δ АВС – прямоугольный и равнобедренный, АН = 0,5АС = 4

2) Δ АН S – прямоугольный, А=30 ◦ , Н S =

S

D

C

H

30°

A

B

8

S

D

C

H

30°

A

B

8

А S =

S

D

C

H

30°

A

B

8

12

1) В правильной пирамиде в основании лежит квадрат.

Δ АВС – прямоугольный и равнобедренный, АН = 0,5АС = 4

2) Δ АН S – прямоугольный, А=30 ◦ , Н S =

3) А S = 2*Н S =

S

D

C

H

30°

A

B

8

S

D

C

K

H

A

B

8

α = arctg

S

D

C

K

H

A

B

8

15

┴

┴

BC

1) ΔSBC – равнобедренный; SK

HK BC

( SBC ; АВС) = SKH = α

2) ΔSHK - прямоугольный,

α = arctg

S

D

C

K

4

H

A

B

8

16

S

Р

D

C

H

A

B

8

BPD

S

Р

D

C

H

A

B

8

1) ΔSDC = ΔSC В – равнобедренные, BP ┴ SC, DP ┴ SC , ( SDC ; S ВС) = BPD =

2) ΔDPB – равнобедренный, DB = , HB = , РН – медиана и высота,

3) по двум углам,

S

4) ΔPHB – прямоугольный,

Р

D

C

K

H

A

B

8

19

S

D

C

K

4

H

A

B

8

64(1 + )

S n =

S

D

C

K

4

H

A

B

8

21

1) АВС D – квадрат, S осн = a 2 = 64.

2) И з ΔSHK по теореме Пифагора:

= = 4

SK = = = =

3) S б = 0,5*Р *SK = 0,5*32*4 = 64

64(1 + )

S

4) S n = S б + S осн =

D

C

K

4

H

A

B

8

22

Задача 2: В правильной треугольной пирамиде сторона основания равна 6 см, высота 12 см. Найдите:

а) боковое ребро пирамиды;

б) угол между боковым ребром и плоскостью основания пирамиды;

в) угол между боковой гранью и основанием пирамиды;

г) двугранный угол при боковом ребре;

д) площадь полной поверхности.

S

12

6

C

B

30°

H

B 1

C 1

A

23

S

12

6

C

B

H

B 1

C 1

A

S В =

S

12

6

C

B

H

B 1

C 1

A

25

1) Так как пирамида правильная, то точка пересечения медиан CC 1 и ВВ 1 является основанием высоты.

2) Δ НС 1 В – прямоугольный, В = 30 ◦ , С 1 В = 3, НС 1 = , НВ = 2 .

3) ΔS НВ – прямоугольный, по теореме Пифагора

S В =

S

12

6

C

B

30°

3

H

B 1

C 1

A

26

S

12

C

B

30°

3

H

B 1

C 1

A

α = arctg

S

12

C

B

30°

3

H

B 1

C 1

A

28

1) ( S В; АВС) = S ВН = α

2) ΔS ВН – прямоугольный,

α = arctg

S

12

C

B

30°

3

H

B 1

C 1

A

29

S

12

C

B

30°

3

H

B 1

C 1

A

β = arctg 4

S

12

C

B

30°

3

H

B 1

C 1

A

31

1) ( S АВ; АВС) = НС 1 S = β

β = arctg 4

2) tg β =

1

S

12

C

B

30°

3

H

B 1

C 1

A

32

S

M

12

C

B

30°

3

H

B 1

C 1

A

AMC =

S

M

12

C

B

30°

3

H

B 1

C 1

A

34

1) ΔS AВ = ΔSC В – равнобедренные, AM ┴ SB , CM ┴ SB ( S АВ; S ВС) = AMC =

1

2) ΔAMC – равнобедренный, МВ 1 ┴ A C , ΔM В 1 А – прямоугольный и sin

1

3) ΔSHC 1 – прямоугольный, SC 1 = , где

HC 1 = * , SC 1 =

1

1

4) по двум углам,

1

S

1

1

5)

M

12

C

B

30°

3

H

B 1

C 1

A

35

S

12

C

B

30°

3

H

B 1

C 1

A

S n =

S

12

C

B

30°

3

H

B 1

C 1

A

37

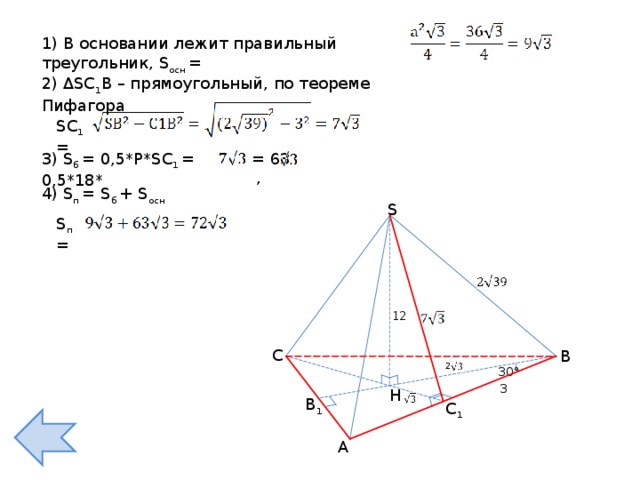
1) В основании лежит правильный треугольник, S осн =

2) ΔS С 1 В – прямоугольный, по теореме Пифагора

S С 1 =

= 63 ,

3) S б = 0,5*Р* S С 1 = 0,5*18*

4) S п = S б + S осн

S

S п =

12

C

B

30°

3

H

B 1

C 1

A

Задача 1 : Основанием пирамиды является равнобедренный треугольник с углом 120 ° . Боковые ребра образуют с плоскостью основания углы по 30 ° . Высота равна 6 см. Найдите площадь полной поверхности пирамиды.

Так как боковые ребра образуют с плоскостью основания равные углы, то основание высоты находится в центре окружности, описанной около Δ АВС. Центр окружности описанной около треугольника находится в точке пересечения серединных перпендикуляров. В треугольнике один из углов тупой, значит, точка пересечения серединных перпендикуляров лежит вне треугольника. SH ┴ пл(АВС), АН = СН = ВН = R .

S

C

6

120 °

P

K

30 °

B

A

H

Задача 1 : Основанием пирамиды является равнобедренный треугольник с углом 120 ° . Боковые ребра образуют с плоскостью основания углы по 30 ° . Высота равна 6 см. Найдите площадь полной поверхности пирамиды.

Так как боковые ребра образуют с плоскостью основания равные углы, то основание высоты находится в центре окружности, описанной около Δ АВС. Центр окружности описанной около треугольника находится в точке пересечения серединных перпендикуляров. В треугольнике один из углов тупой, значит, точка пересечения серединных перпендикуляров лежит вне треугольника. SH ┴ пл(АВС), АН = СН = ВН = R .

S n = )

S

C

6

120 °

P

K

30 °

B

A

H

1. Δ А SH – прямоугольный, А=30 ◦ и SH =6 АН = SH = 6 – радиус описанной окружности.

2. Δ А H С = Δ С H В – равносторонние АС = СВ = 6 см.

S АВС = см 2 .

AC = 3 , АК = СК* = *3 = 9 см.

3. Δ АСК – прямоугольный, С=60 ◦ , АС = 6 CK =

4. Δ А S С = Δ С S В, высоты, опущенные в этих треугольниках из вершины S будут равными. ΔS НР – прямоугольный, где Р – середина СВ, по теореме Пифагора:

S Р = = = см.

S

ΔS НК – прямоугольный, по теореме Пифагора:

см.

6. S б = 2*S SCB + S ASB = 2*

C

6

см 2 .

120 °

P

K

30 °

9

S п = S б + S осн =

B

A

см 2 .

H

41

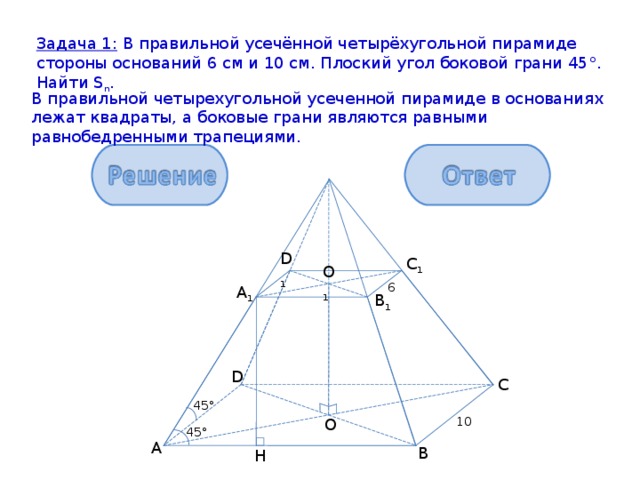
Задача 1: В правильной усечённой четырёхугольной пирамиде стороны оснований 6 см и 10 см. Плоский угол боковой грани 45°. Найти S n .

В правильной четырехугольной усеченной пирамиде в основаниях лежат квадраты, а боковые грани являются равными равнобедренными трапециями.

D 1

C 1

O 1

6

A 1

B 1

D

C

45 °

10

O

45 °

A

B

H

Задача 1: В правильной усечённой четырёхугольной пирамиде стороны оснований 6 см и 10 см. Плоский угол боковой грани 45°. Найти S n .

В правильной четырехугольной усеченной пирамиде в основаниях лежат квадраты, а боковые грани являются равными равнобедренными трапециями.

S n = 200

D 1

C 1

O 1

6

A 1

B 1

D

C

45 °

10

O

45 °

A

B

H

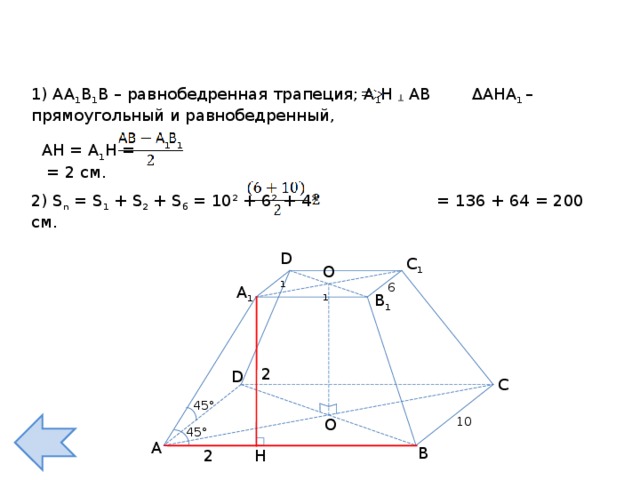
1) АА 1 В 1 В – равнобедренная трапеция; А 1 Н ┴ АВ Δ АНА 1 – прямоугольный и равнобедренный,

1

1

АН = А 1 Н = = 2 см.

2) S n = S 1 + S 2 + S б = 10 2 + 6 2 + 4 * = 136 + 64 = 200 см.

D 1

C 1

O 1

6

A 1

B 1

2

D

C

45 °

10

O

45 °

A

B

2

H

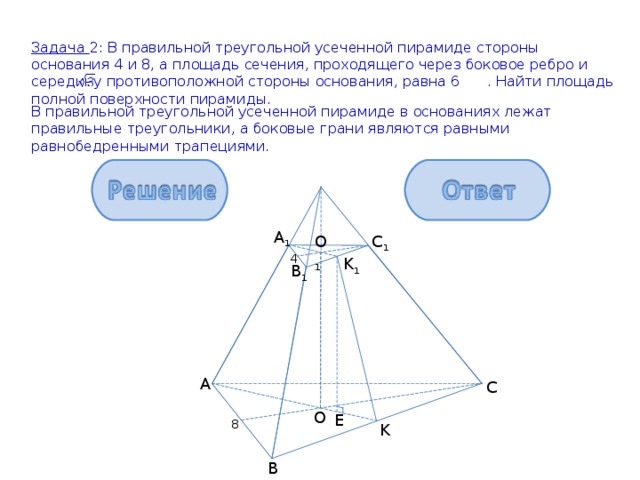
Задача 2: В правильной треугольной усеченной пирамиде стороны основания 4 и 8, а площадь сечения, проходящего через боковое ребро и середину противоположной стороны основания, равна 6 . Найти площадь полной поверхности пирамиды.

В правильной треугольной усеченной пирамиде в основаниях лежат правильные треугольники, а боковые грани являются равными равнобедренными трапециями.

A 1

C 1

O 1

4

K 1

B 1

A

C

O

E

8

K

B

Задача 2: В правильной треугольной усеченной пирамиде стороны основания 4 и 8, а площадь сечения, проходящего через боковое ребро и середину противоположной стороны основания, равна 6 . Найти площадь полной поверхности пирамиды.

В правильной треугольной усеченной пирамиде в основаниях лежат правильные треугольники, а боковые грани являются равными равнобедренными трапециями.

S n = 44

A 1

C 1

O 1

4

K 1

B 1

A

C

O

E

8

K

B

1) S ABC = = 16 ; S A B C = = 4

1

1

1

2) КК 1 – высота боковой грани.

1

1

3) S сеч = h = = = 2

1

1

А 1 К 1 = ; АК =

4) К 1 Е ┴ АК и ЕК = ОК - ОЕ = ОК - О 1 К 1 ;

ОК = АК = * = ;

О 1 К 1 = А 1 К 1 = * = ;

ЕК = - =

A 1

O 1

C 1

5) Из прямоугольного Δ К 1 ЕК по теореме Пифагора:

4

K 1

B 1

КК 1 = = = =

1

2

1

2

6) S б = *К 1 К = =

= 24

A

C

7) S n = 16 + 4 + 24 = 44

O

E

8

K

B

Задача 3: Основанием пирамиды является прямоугольник, диагональ которого равна 8 см. Плоскости двух боковых граней перпендикулярны к плоскости основания, а две другие боковые грани образуют с основанием углы в 30 ◦ и 45 ◦ . Найдите площадь поверхности пирамиды.

Так как плоскости двух боковых граней перпендикулярны к плоскости основания, то боковое ребро, по которому пересекаются боковые грани также перпендикулярно к плоскости основания. Это боковое ребро является высотой пирамиды.

M

B

A

8

D

C

Задача 3: Основанием пирамиды является прямоугольник, диагональ которого равна 8 см. Плоскости двух боковых граней перпендикулярны к плоскости основания, а две другие боковые грани образуют с основанием углы в 30 ◦ и 45 ◦ . Найдите площадь поверхности пирамиды.

Так как плоскости двух боковых граней перпендикулярны к плоскости основания, то боковое ребро, по которому пересекаются боковые грани также перпендикулярно к плоскости основания. Это боковое ребро является высотой пирамиды.

S пир = 8(3 + 3 + 3 )

M

B

A

8

D

C

1) Предположим, что плоскости МАВ и MAD перпендикулярны к плоскости основания, тогда линия их пересечения МА перпендикулярна к плоскости основания, т. е. МА — высота пирамиды.

┴

┴

2) Так как СВ АВ, то СВ МВ по теореме о трех перпендикулярах, поэтому MBA — линейный угол двугранного угла при ребре СВ, MBA = 30°.

Аналогично AD DC , MD DC , MDA — линейный угол двугранного угла при ребре DC , MDA = 45°. Треугольники МВС и MDC прямоугольные.

┴

┴

3) Пусть MA = х см, тогда МВ = 2х см, АВ = х см. Из ΔMAD имеем: МА = AD = x см, MD = х см. Из Δ АВС получаем: АВ 2 + ВС 2 = АС 2 , 3х 2 + х 2 = 64, х 2 = 16, х = 4 (см).

4) Таким образом, МА = 4 см, АВ = DC = 4 см, МВ = 8 см, MD = 4 см, AD = BC = 4 см. 

M

S бок = АВ*АМ + А D *АМ + ВС*ВМ + D С* D М =

= *4 *4 + *4*4 + *4*8 + *4 *4 = 24 + 8 +

+ 8 

S осн = 4 *4 = 16 

S пир = 24 + 24 + 8 = 8(3 + 3 + 3 )

2х

х

B

30°

A

45 °

8

х

D

C

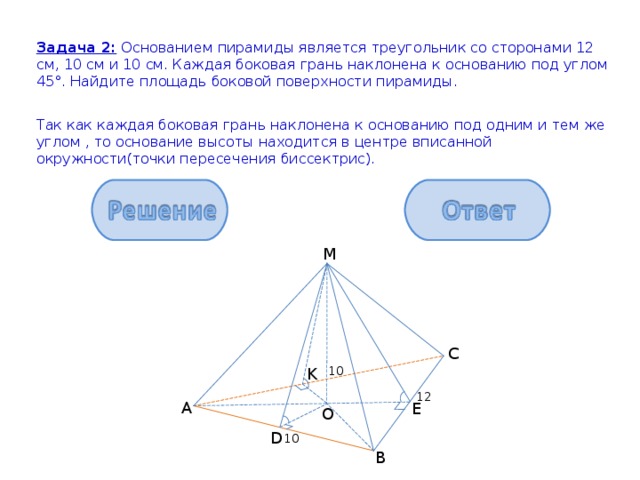
Задача 2: Основанием пирамиды является треугольник со сторонами 12 см, 10 см и 10 см. Каждая боковая грань наклонена к основанию под углом 45°. Найдите площадь боковой поверхности пирамиды.

Так как каждая боковая грань наклонена к основанию под одним и тем же углом , то основание высоты находится в центре вписанной окружности(точки пересечения биссектрис).

M

C

10

K

12

A

E

O

D

10

B

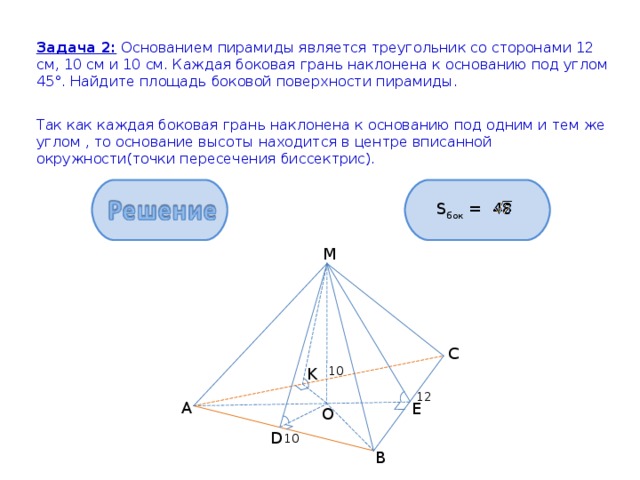
Задача 2: Основанием пирамиды является треугольник со сторонами 12 см, 10 см и 10 см. Каждая боковая грань наклонена к основанию под углом 45°. Найдите площадь боковой поверхности пирамиды.

Так как каждая боковая грань наклонена к основанию под одним и тем же углом , то основание высоты находится в центре вписанной окружности(точки пересечения биссектрис).

S бок = 48

M

C

10

K

12

A

E

O

D

10

B

1) АВ = АС = 10 см, ВС = 12 см, МО — высота пирамиды, АЕ — высота и медиана к стороне ВС треугольника АВС. Из Δ АВЕ получаем: ВЕ = 6 см, АЕ = 8 см. S АВС = 6*8 = 48 см 2 .

2) Пусть OD и ОК — перпендикуляры к сторонам треугольника АВС, тогда МЕО, MDO , MKO — линейные углы двугранных углов, образованных плоскостями боковых граней и основанием пирамиды. МЕО = MDO = MKO = 45°, Δ МЕО = ΔMDO = Δ МКО (ПО катету МО и противолежащему острому углу в 45°), поэтому OE = OD = OK , т. е. точка О —

центр окружности, вписанной в основание пирамиды. Пусть ОЕ = г. Тогда r = = = 3 см (р — полупериметр Δ АВС).

ABC

M

3) Из Δ МОЕ получаем: ОЕ = 3 см, МЕ = = З см

MD = MK = ME = 3 см

4) S бок = (AB + BC + AC)*ME = (10 + 12 + 10)* З =

= 48

см 2

C

10

K

12

A

E

O

D

10

B