Факультатив по математике для 6-А, 6-Б и 6-В классов Тема: «Элементы комбинаторики и теории вероятностей. Комбинации. Дерево возможных вариантов»

Комбинаторика – это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.

• С комбинаторными задачами люди столкнулись в глубокой древности. В Древнем Китае увлекались составлением магических квадратов. В Древней Греции занимались теорией фигурных чисел.
• Комбинаторные задачи возникли и в связи с такими играми, как шашки, шахматы, домино, карты, кости и т.д.
• Комбинаторика становится наукой лишь в 18 в. – в период, когда возникла теория вероятности .

Значительный вклад в развитие комбинаторики внес Леонард Эйлер (1707-1783)

Он рассматривал задачи о разбиении чисел, о паросочетаниях, циклических расстановках, о построении магических и латинских квадратов, положил начало совершенно новой области исследований, выросшей впоследствии в большую и важную науку—топологию, которая изучает общие свойства пространства и фигур.

Методы решения комбинаторных задач

• Правило суммы.
• Правило произведения.
• Графы (деревья).

Правило суммы

• Если элемент А может быть выбран К1 способами, а элемент В – К2 способами, причем выборы А и В являются взаимно исключающими, то выбор «либо А, либо В» может быть осуществлен К1+К2 способами .

Задача 1. Сколько существует способов выбрать кратное двум или трем число из множества чисел : 2,3,4,15,16,20,21, 75,28 ?

Решение: К1=5 –кратное 2 (2,4,16,20,28),

К2=4 – кратное 3 (3,15,21,75)

К1+К2 = 5+4 = 9

Правило произведения

• Если элемент А может быть выбран К1 способами, а элемент В – К2 способами, то выбор «А и В» может быть осуществлен К1 х К2 способами .

Задача 2. а) Сколько различных двузначных чисел можно составить из цифр 1, 3, 5, 7, 9?

Решение: N= 5х5 = 25 ( Если не сказано, что элемент не повторяется, то выборка с повторениями)

б) Сколько среди них чисел, кратных 5?

Решение: Число кратно 5, если оканчивается цифрой 5 или 0. В нашем случае – 5.

На первой позиции фиксируем одну из пяти цифр, на второй – 5.

N= 5 х1 =5

в) Сколько среди них чисел, кратных 11?

Решение : Двузначное число кратно 11, если обе его цифры одинаковы. N= 5

г) Сколько среди них чисел, кратных 3?

Решение : Число кратно 3, если сумма его цифр делится на 3. Составим всевозможные пары:

1 – 1 3 – 3 5 – 5 7 – 7 9 – 9

1 – 3 3 – 5 5 – 7 7 – 9

1 – 5 3 – 7 5 – 9

1 – 7 3 – 9

1 – 9

Таких пар 15. Среди них 5 пар, сумма которых делится на 3, причем три пары допускают перестановку, т.е. могут образовать по два разных числа. Всего 5+3=8 различных двузначных чисел.

Задача 3 . Сколько существует способов занять 1-ое, 2-ое и 3-е места на чемпионате по футболу, в котором участвуют

а ) 10 команд?

Решение: N= 10х9х8=720

б ) 11 команд?

Решение: N= 11х10х9=990

Задача 4. Сколько различных двузначных чисел можно составить из цифр 0, 1,2,3,4 , если

а ) цифры не повторяются?

Решение: На первом месте одна из 4-х цифр ( 0 не может быть), на 2-ом – одна из оставшихся 4-х:

N= 4х4= 16

б ) цифры могут повторяться

Решение : На 1-ом месте может быть одна из 4-х цифр, на 2-ом – одна из 5 ( 0 входит):

N= 4х5= 20

Подсчет вариантов с помощью графов

При встрече каждый из друзей пожал другому руку. Сколько было рукопожатий, если друзей :

а) трое ; б) четверо ; в) пятеро?

N=3 N=6 N=10

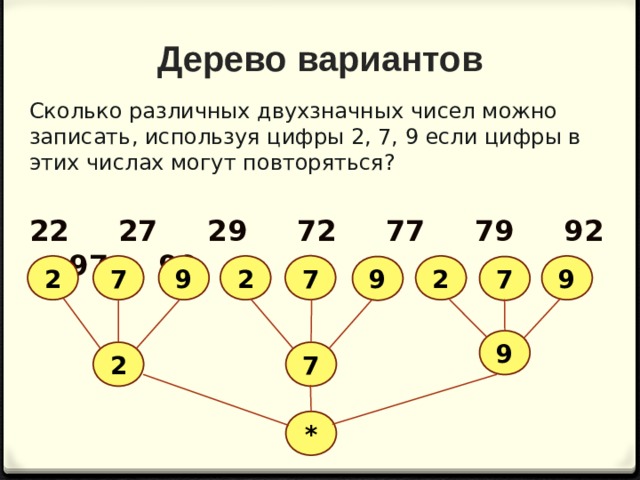
Дерево вариантов

Сколько различных двухзначных чисел можно записать, используя цифры 2, 7, 9 если цифры в этих числах могут повторяться?

22 27 29 72 77 79 92 97 99

7

2

7

2

9

2

9

7

9

9

2

7

*