С6 Задачи на кол-во корней уравнения
Множества значений, числа решений уравн f(x)=a
1)Постр график функции и с его пом определить мн-во зн, прин функц в 2, 3 и б
точках; а также опр макс число корней уравн f(x)=a 
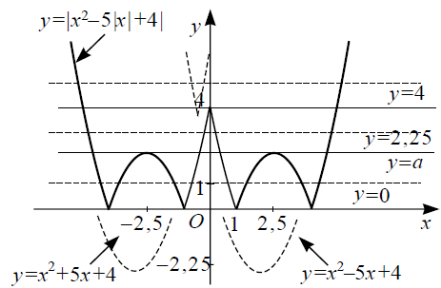
1) Найдите все зн a, при каждом из кот график фу 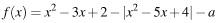 пересек ось абсцисс менее чем в 3 разл точках.
пересек ось абсцисс менее чем в 3 разл точках.
Реш рассм вспомо функ 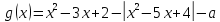
График 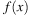 перес ось абсцисс в 2 или менее т, если ур
перес ось абсцисс в 2 или менее т, если ур 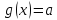 имеет менее 3 разл корней.
имеет менее 3 разл корней.
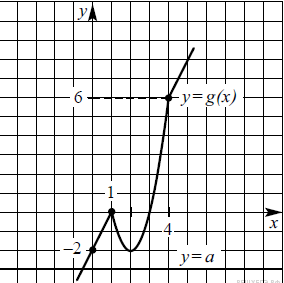 Если
Если 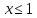 или
или 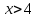 то
то 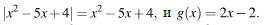
Если 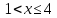 то
то 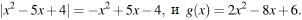 График функции f(x) состоит из двух лучей и дуги параболы. На рис видно, что ур-е
График функции f(x) состоит из двух лучей и дуги параболы. На рис видно, что ур-е 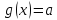 имеет менее 3 корней, только если
имеет менее 3 корней, только если 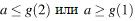 т е при
т е при  или
или 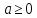 отв
отв 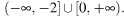
6) (ЕГ2010). Найти все зн a , при каждом из кот любая прямая, перпенд оси ординат имеет неч число общих точек с графиком функции
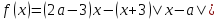
7)При каких a ур имеет ровно 3 корня?
Параллельный перенос
1) Для каждого зн парам  опр число реш уравн
опр число реш уравн  .
.
Реш. Построим график функции 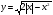 .
.
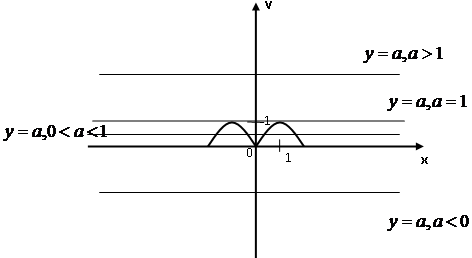 Рассм
Рассм  . Это прямая паралл оси ОХ.
. Это прямая паралл оси ОХ.
Отв. Если 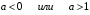 , то реш нет;если
, то реш нет;если 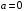 , то 3 реш;
, то 3 реш;
если  , то 2 реш; если
, то 2 реш; если  , 4 реш.
, 4 реш.
Графический метод
Линейные с модулем
0)Найдите все зн парам а, при каждом из кот ур 
имеет единственный корень. Ответ: 0; 1.
Отв: если a 1;5,0 , нет реш; если a -,- 1] 0.5 (1,+)-1 реш; при a (-1,0.5) -2 реш
Квадратные и сводящиеся к ним
5)Найди мн-во всех  , для кот ур
, для кот ур  имеет 2 разл корня.
имеет 2 разл корня.
Реш Перепишем данное ур в виде:
Отв. При  , или
, или  , или
, или  .
.
Иссл кол-во решений в з-ти от параметра а
N1 Найдите все зн парам а, при каждом из кот нер-во
имеет единств целое реш Отв: −1, 5
N2 Найдите все зн парам а, при каждом из кот нер-во имеет единств целое реш Отв:
5)Найди мн-во всех  , для кот ур
, для кот ур  имеет 2 разл корня.
имеет 2 разл корня.
Реш Перепишем данное ур в виде:
Ответ. При  , или
, или  , или
, или  .
.
нелинейные
Пр1 При каких  ур
ур  имеет решение?
имеет решение?
Реш Рассм функ  . Иссл ее на монотон- она возр на
. Иссл ее на монотон- она возр на  и убыв на
и убыв на  . Т
. Т  - т максим.
- т максим.  - это сем прямых, прох через т
- это сем прямых, прох через т  .
.
Симметрия
МИОО Найти все а при кот ур-е имеет ровно 6 Реш, где f четная периодич функц с пер T =2, опр на всей числ прям,  при
при  .
.
График полуx сдвигом на 2k ед вдоль Ox из ее графика на [1; 1] .
Если a = 0 , то f (x)=0, и график имеет с y =5x единств общую точку
Если  то в силу четн f(x) при
то в силу четн f(x) при  и
и 
Пусть a 0 6 реш воз, если прямая y = (2a+ 5)x прох через n A(5; a) Но из у a = 3(2a+ 5)получ a =2,5, т.е. положит реш нет. След, сл a 0 не возм
Пусть a 0 рис). Ровно 6 реш возм, если прямая y =|2a+ 5|x прох через тB(-5; a). Из ур  получ
получ 
МИОО Найти все а при кот ур-е имеет ровно 6 Реш, где f четная периодич функц с пер T =16/3, опр на всей числ прямой,
МИОО Найти все а1 при кот ур-е имеет ровно 6 Реш, где f четная периодич функц с пер T =4, опр на всей числ прямой, при
Использование условия касания
МИэт При каких зн p и q парабола  касается прямых
касается прямых

Отв 
4. При каких зн параметра a уравнение имеет 1 решение
Реш. Переходим к с-ме уравн
1 уравн опр верх ветвь параболы с верш на оси абсцисс т x=2/3 2е опред прямую с угл коэфф k=1, т е угол наклона к оси абсцисс= 45º, а отрезок, отсекаем на оси ординат= a (рис1). Если данн прямая – касат к параболе, то параб и прямая имеют 1 общ точку – т касания. Дифф ур параболы и прир произв=1 получ абсциссу т касания:
Определим зн параметра a, соотв знач x=17/12
Две т пересеч параболы и прямой м получить, если прямая прох через верш параболы паралл касательн, т е пересек ось ординат в т y=-2/3 а знач параметра в этом сл a=-2/3
Если прямую перемещать паралл самой себе вниз, т е знач парам а
и так как x2/3 то
Отв. При a=1/12 корень уравн x=17/12 при a
500370 Найти все а уравн имеет 2 корней на 

реш при a
с прямой р или с прямой m, то гр б иметь 2общ т 3 общие точки,если прямые y = ax − 1 лежат
внутри острого угла, образов прямыми p и m.
При найд зн парам прямая m пересек с графиком  в т
в т
а прямая р касается графика в т 2 cпособ через касательную cложнее
501070 Найти все a при каждом из кот уравн на промеж 
имеет больше 2 корней. Отв
500135 Найти все a при каждом из кот ур  имеет 12корнz на
имеет 12корнz на 
отв
500350 Найдите все зн а, при кот ур на промеж  имеет ровно 2 корня.
имеет ровно 2 корня.
Отв при
500216 Найдите все зн при каждом из кот уравн имеет 2 корней.
при  ур имеет 2 реш, а при больших a — только 1 реш единств промеж где 3 реш
ур имеет 2 реш, а при больших a — только 1 реш единств промеж где 3 реш
485982 При каких уравн имеет ровно 3 корня?
Реш. Запишем ур в виде
2) Найдите все зн парам а , при каждом из кот уравн
имеет хотя бы 1 реш.
№50) Найди все положит зн пар а, при каждом из кот уравн  имеет единст реш.
имеет единст реш.
Реш. g(x) - непр, строго возр на всей обл опр и м приним любое зн в
g(x) - непр, строго возр на всей обл опр и м приним любое зн в При 0 т е ур f(x) = g(x) имеет ровно 1 реш.(рис.1) При a = 1 f(x) =1, и ур f(x) = g(x) также имеет единств реш x=1.
При 0 т е ур f(x) = g(x) имеет ровно 1 реш.(рис.1) При a = 1 f(x) =1, и ур f(x) = g(x) также имеет единств реш x=1.
При a 1:


У произв единств 0. Слева о h(x) убыв, справа - возр. Поэтому она либо вообще не имеет 0, либо имеет два 0. И 1 корень она имеет только в том сл, когда он совп с найд экстр.Т е, нам треб найти такое a, при кот  дост экстр и обращ в - в 1 и той же то. Т е, когда прямая y=x явл касат к графику функции
дост экстр и обращ в - в 1 и той же то. Т е, когда прямая y=x явл касат к графику функции  . (рис.2)
. (рис.2)
Т е 
 Откуда : x*ln(a) = 1, откуда ln(a)=1/x,
Откуда : x*ln(a) = 1, откуда ln(a)=1/x, 
Снова подст во 1е ур: x = e. 
 отв (0;1] и {e(1/e)}
отв (0;1] и {e(1/e)}
1)При каких зн парам  ур
ур  имеет единств решение?
имеет единств решение?
Рассм ф  и
и  . График 2й фун – это полуокруж с ц в т С
. График 2й фун – это полуокруж с ц в т С  и рад =1
и рад =1  , дуга АВ. Угл кооф ОА= 1/3 ОВ =1/5. Угл коэфф касат=8/15. Легко находится из системы
, дуга АВ. Угл кооф ОА= 1/3 ОВ =1/5. Угл коэфф касат=8/15. Легко находится из системы
Итак, прямые сем  имеют с дугой только 1 общую точку при
имеют с дугой только 1 общую точку при  .
.
505569 Опр, при каких зн парам а ур имеет ровно 2 реш.
Реш  тогда
тогда
Если а=0, то уравнение не имеет реш. Если a
Если a0 ур имеет единств реш ттолько , когда прямая y=x касается графика функ
Ответ







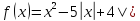

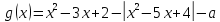
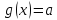 имеет менее 3 разл корней.
имеет менее 3 разл корней. Если
Если 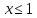 или
или 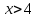 то
то 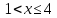 то
то  или
или 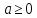 отв
отв 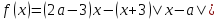
 опр число реш уравн
опр число реш уравн  .
.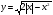 .
.  Рассм
Рассм  . Это прямая паралл оси ОХ.
. Это прямая паралл оси ОХ. 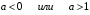 , то реш нет;если
, то реш нет;если 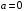 , то 3 реш;
, то 3 реш;









